基于博弈赋值的渡江工程信息保障指标价值系数研究*

王凤山，郭子曜

（陆军工程大学野战工程学院，南京 210007）

0 引言

渡江工程信息保障，作为支撑遂行渡江工程保障行动的核心任务之一，其效能评估和体现受指挥决策、战场态势等多重因素影响，各因素之间包含物质、能量与信息的交互和衍化作用，导致不同单一赋值法求得的结果偏差较大，且易受离散极值或主观偏差影响，鲁棒性较差。因此，如何科学判别渡江工程信息保障特征指标，科学量测其价值系数，合理优化渡江工程信息保障指标排序，是渡江工程信息保障效能评估的关键步骤。

渡江工程信息保障指标价值系数度量，其实质是寻求定性、定量指标的一致性关系，解决渡江工程信息保障资源与任务需求之间矛盾。渡江工程信息保障指标价值系数研究问题，难以建立显式表达的数学模型，是典型的复杂多属性决策问题。集成博弈论方法应用于渡江工程信息保障指标价值系数度量，寻求基于信息熵和反熵得到的两种价值系数的一致或妥协，以期解决两个及两个以上因素在对抗性或竞争性局势下的科学决策问题，实现对渡江工程信息保障指标价值系数客观、合理、科学的判定。

1 渡江工程信息保障效能评价指标体系

1.1 价值系数相关理念

价值系数概念来源于价值工程（value engineering，VE），其作用在于帮助决策人员针对价值工程进行功能分析时找到薄弱环节，基于产品功能与成本的线性变换方法，实现功能、成本到产品价值的映射变换。

价值系数是决策者寻找最佳方案的数据支撑，其核心在于保持产品必要功能的前提下降低产品成本。遵循价值系数的计算方法和规则，对渡江工程信息保障指标进行价值系数定量分析，在保持其整体功能的前提下合理优化指标排序，以寻求渡江工程信息保障效能评估的合理指标。

1.2 渡江工程信息保障指标价值特征描述

价值系数从研究对象所必备的功能、特征、成本等因素为出发点，以功能分析为核心，在分析对象价值特征的基础上来研究对象的功能和效用等问题，广泛应用于金融分析、工程方案等领域，适应工程保障行动效能评估的应对要求。

挖掘指标体系的价值特征机理和构建过程，其实质就是对各评价指标进行深入研究和系统分析。以对渡江工程信息保障价值特征分析及提取作为重点目标，把握模型与指标、整体与局部的系统特征，实现对渡江工程信息保障效能评价指标体系描述，如图1 所示。

图1 中，通过效能评价指标体系分析流程，论证渡江工程信息保障任务流程框架和指标、模型体系的科学性和一致性，以促进感性到理性、定性到定量的功能转变，为渡江工程信息保障效能评估指标体系层次的建立提供模型支持与服务。

1.3 渡江工程信息保障价值特征层次

区别于价值工程项目，渡江工程信息保障效能评价指标的价值度量范畴除功能、成本外，更多的是以战场态势发展为进程的指挥、防护、数据链等作战模块的效能发挥，满足为渡江工程信息保障效能评价提供支持和服务的要求。

指标体系是指由多个彼此关联、相互联系的评价指标，基于一定的规则、层次建立的整体。结合图1 的指标价值特征描述，挖掘、分析影响渡江工程信息保障的因素，如下页图2 所示。

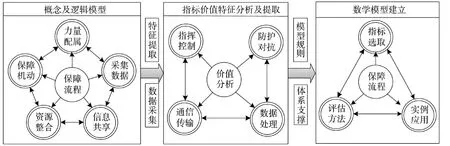
图1 指标价值特征分析流程

图2 中，遵循评估指标的实战化和典型性特征，按照科学、量化、实用、易获的原则，设计渡江工程信息保障效能价值评价层次，主要包括指挥控制价值、防护对抗价值、通信传输价值以及数据处理价值4 类。

图2 渡江工程信息保障效能价值评价层次

2 渡江工程信息保障指标价值系数计算

2.1 信息熵计算指标价值系数

信息熵作为一种度量无序程度的客观方法，在工程技术、社会经济等领域取得了十分广泛的应用。其核心思想是通过计算指标的变异程度来反映出指标熵值的大小：熵值越大，反映出该指标信息的稳定性越差，价值系数越小；反之，熵值越小，则该指标信息的稳定性越好，对应价值系数越大。

采取极差法对评价方案S在指标A上的量测值α进行标准化处理。

若指标A呈现max 型，则标准化赋值β越大，渡江工程信息保障效能越好，如式（2）。

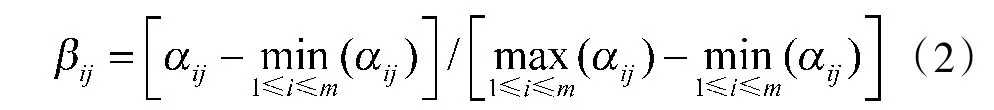
若指标A呈现min 型，则标准化赋值β越大，渡江工程信息保障效能越差，如式（3）。

式中，为了避免指标数据为0，引入常量k。根据信息熵理论的熵值计算方法，渡江工程信息保障效能评价指标A的熵值为式（6）。

式中，δ表示渡江工程信息保障效能评估指标A的信息熵值。

以1-δ反应指标的变异程度，其变异程度与指标相对价值系数大小成正比。根据信息熵基本原理，计算指标A的相对价值系数θ，如式（7）。

则渡江工程信息保障效能评价指标A的价值系数ρ表示为式（8）。

2.2 反熵法计算指标价值系数

传统信息熵受样本容量限制，且指标差异度呈现出较强敏感性，在分配相对价值系数时易出现个别值过大或过小的情况，面向指标数据为0 和1 时所得熵值均无限趋向于0，显然容易导致重要信息的缺失。

反熵法对指标差异度呈现出较弱敏感性，在最大限度减少信息损失的同时，又较好地体现指标之间的差异性，且该方法具备样本容量要求低、原始数据利用率高等特征，能够有效避免人为因素的干扰，得到的价值系数真实性强、可靠性高。

根据式（1）～式（5），计算渡江工程信息保障效能评估指标A的反熵值，如式（9）。

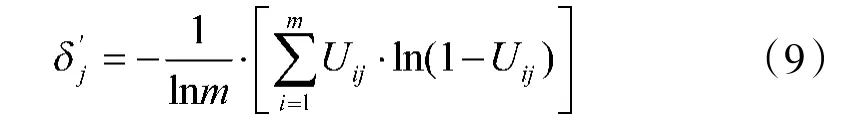
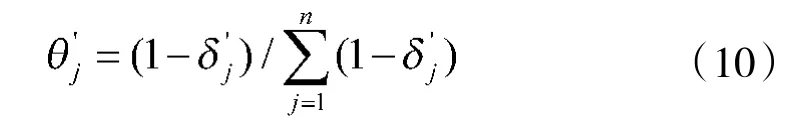
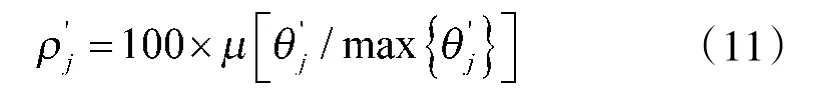
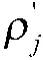
2.3 博弈均衡的指标价值系数组合赋值

博弈论作为一门发展较为成熟的方法论，其核心是在博弈中寻求均衡，主要为决策者在多个因素竞争、对抗情况下作出决策提供思路。

考虑不同单一赋值法得到的价值系数偏差较大，这就需要考量两种方法间的竞争与均衡关系，协调信息熵、反熵求得的价值系数之间冲突，最大限度保留两种熵值所蕴含的重要信息。基于此，引入博弈模型，以纳什均衡为协调目标进行组合赋值计算，其基本原理如下：

根据博弈赋值的思想，对以上两个价值系数进行最优的线性组合，以离差最小化为目标，对两个线性组合系数h、h进行优化，得到最合理的价值系数，由此确定目标函数如式（13）。

其中，E 为任意价值系数的线性组合，e为任意单一赋值法确定的价值系数e、Δe。利用矩阵微分性质将式（13）等价变换为最优化一阶导数条件的线性方程组，具体如式（14）。

根据式（14）求得最优化的线性组合系数h、h，并进行归一化处理，得到基于博弈均衡的指标价值系数如式（15）。

其中，归一化公式如式（16）。

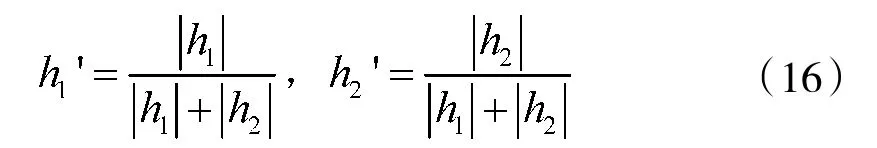
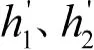
3 计算分析

3.1 指标价值系数评价初始矩阵

假设渡江工程信息保障指标案例评价样本，设计其指标价值系数评价初始矩阵，见表1。其中，假设S，S，S，S满足评价方案的独立性，即评价方案之间无先后次序性关联，同时为便于计算，取k=0.01。

表1 指标价值系数评价初始矩阵

3.2 价值系数计算

由式（1）～式（11），分别计算基于信息熵和反熵法的价值系数，为了使得理想的综合价值系数与各单独价值系数的偏差极小化，最大限度保留信息熵、反熵法所体现的隐藏信息，采取以纳什均衡为协调目标的博弈模型进行综合赋值计算，并基于此进行价值系数计算。

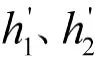
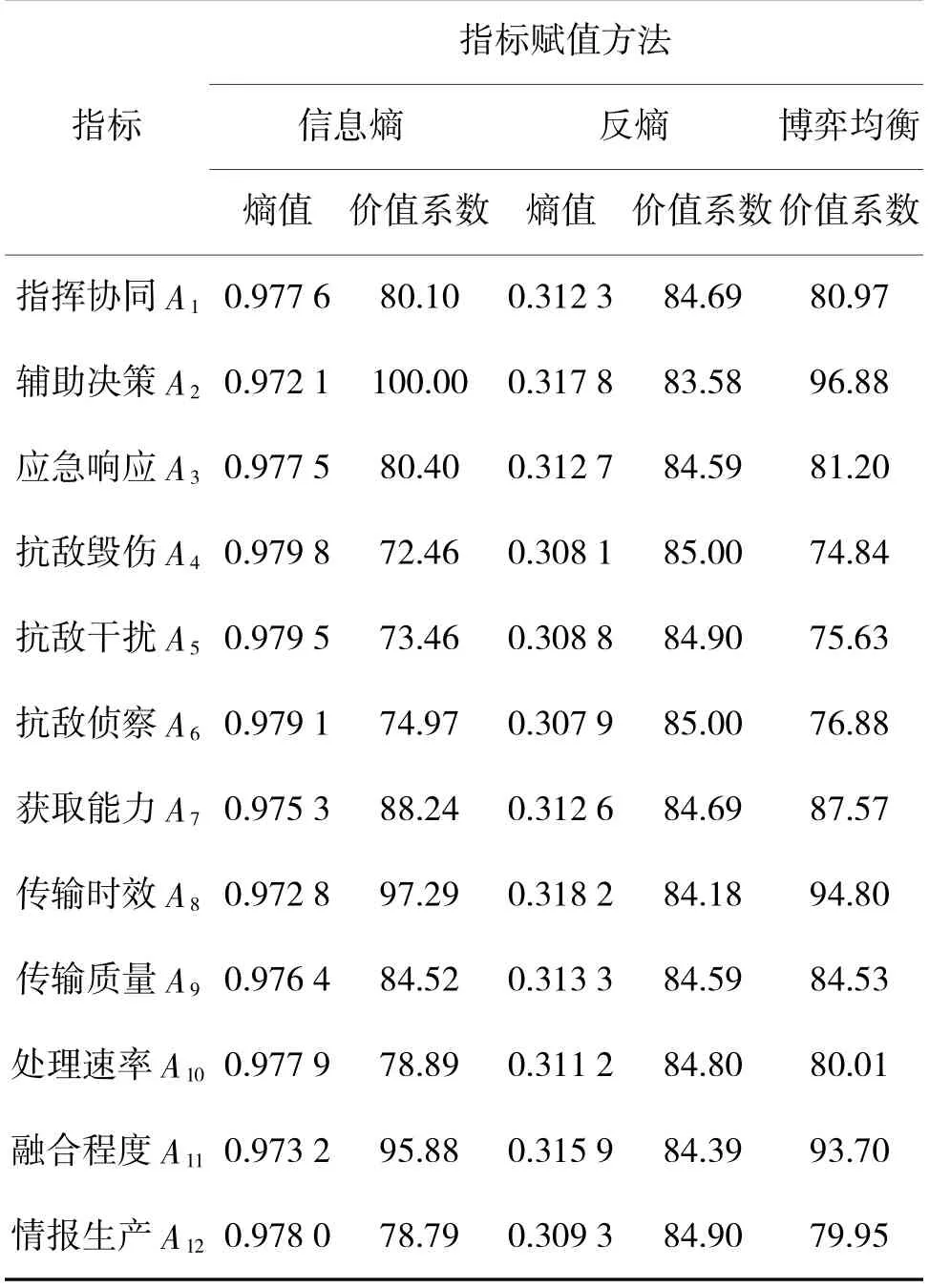
表2 指标相对价值系数

根据表2 分析可得：信息熵赋值方式稳定性较差，体现在某些指标的相对价值系数波动较大，这是由于信息熵对指标差异度的敏感性较大，导致某些指标对整体效能评估的贡献度被过度增强和削弱；反熵法评价结果趋于平稳，避免了部分指标失效或相对价值系数过大的极端情况，但同时也存在各指标相对价值系数过于接近，无法体现出指标相对价值系数差异度的缺陷，结合指标相对价值系数折线图进一步比对分析，如图3 所示。

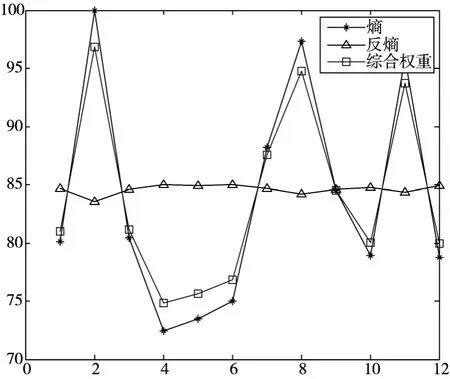
图3 指标相对价值系数折线图

图3 为指标价值系数折线图。根据图中信息可知，基于博弈模型的综合赋值与信息熵的赋值趋于同向变化，根据离差极小化对各指标价值系数进行纳什均衡，克服了单一赋值方法的片面性，又能根据实际运行经验反映专家的主观意见，因此，能更加科学有效地区分不同指标的重要程度。

结合表2 中的指标价值系数进行柱状图对比，具体如图4、图5 所示。

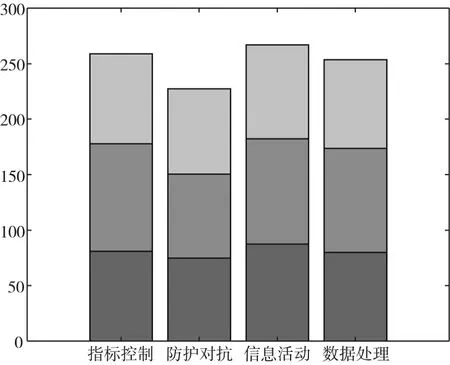
图4 基于博弈均衡的准则价值系数对比

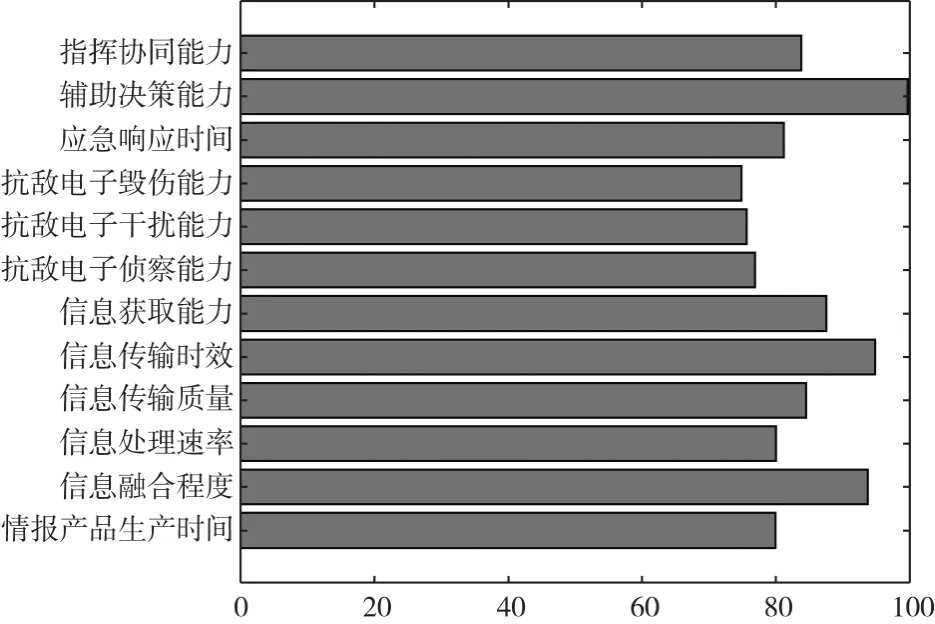
图5 基于博弈均衡的指标价值系数对比

根据表2 对渡江工程信息保障指标予以排序：A，A，A，A，A，A，A，A，A，A，A，A。同时，根据图4、图5 分析渡江工程信息保障指标价值系数的数值特征可知，准则层中防护对抗B价值系数明显低于其他准则，且其中各指标的价值系数区分度较低，一定程度上反映了渡江工程信息保障对防护对抗的需求较小；通信传输B价值系数最高，在整个指标体系中呈现出较大影响力，映射出信息采集、传输等活动在渡江工程信息保障中的重要性；另外，辅助决策能力A和信息融合程度A的价值系数较高，在渡江工程信息保障中扮演了重要角色，需要决策者在指标选取时予以关注。

3.3 对比分析

为了考量博弈赋值得到价值系数的科学性和有效性，选取均方差模型对指标数据进行价值系数度量和分析，结果如下：

图6 中，博弈赋值模型与均方差模型下的计算结果基本符合，均方差模型下的指标价值系数梯度明显，而博弈赋值模型下结果较为平缓。挖掘指标与整体的内在关系和机理，考察个体价值系数与整体价值度量的联系和冲突，均方差模型下指标间价值系数的差异性给整体价值度量带来了系统性风险，容易导致在价值系数研究中对个别指标产生分析偏差，博弈模型更多保留了指标与整体间的信息特征和内在联系，能够为指标价值系数的度量提供科学解释和说明。

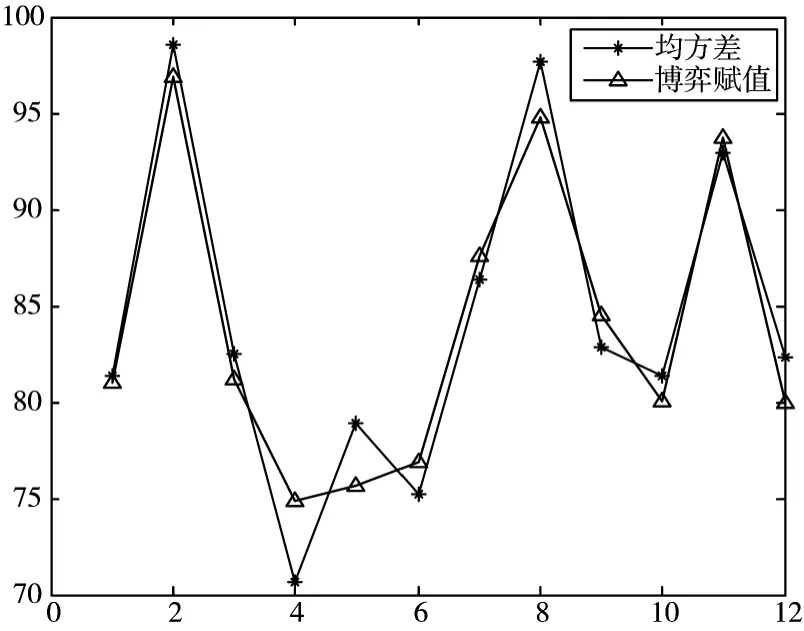
图6 不同模型计算结果比对

4 结论

利用博弈均衡原理与方法，对渡江工程信息保障效能评估指标进行价值系数研究，得到如下结论：

1）设计渡江工程信息保障指标体系，给出熵、反熵的指标相对价值系数计算方法，为渡江工程信息保障指标的价值系数研究提供理论基础。

2）引入价值系数实现渡江工程信息保障指标的有效度量，为指标的横向决策和纵向对比提供量化方法。

3）为克服传统方法的缺陷，在利用两种单一赋值方法的基础上，结合博弈模型与纳什均衡协调为目标进行组合赋值计算，协调和均衡了两种赋值的作用和影响。

4）案例表明，基于纳什均衡协调的博弈模型能够准确、全面地挖掘样本价值信息，能有效克服指标价值系数研究中出现的信息片面问题。

渡江工程信息保障指标并非固定、统一的系统，需要面向不同任务目标、作战态势予以增减，因此，在模型实际运用时需要把握其特殊性、针对性。如何解析渡江工程信息保障指标内在联系的发展机理，探索局部指标价值系数与整体系统目标价值的变化规律，提高模型的可行性和适用性，是渡江工程信息保障指标价值系数研究需要进一步解决的问题。