唐代数学教材初探

吴洪成，张美玲

（1.河北大学 教育学院,河北 保定 071002；2.保定市徐水区巩固庄中学，河北 保定 071002）

隋唐时期，经历战乱动荡历史之后，国家复归于统一。唐代封建统治者为巩固政权，推动各项社会改革，国力不断上升，号称大唐盛世，尤以“贞观之治”为代表。国家经济实力的增强，有助于民众安居乐业，由此推动了自然科学的发展。唐代数学教育取得重大成果，数学专科学校陆续建立，大批优质数学教材涌现，数学教材的成就在中国教材史上占据重要位置。本文拟在梳理唐代数学教育状态的基础上，呈现数学教材类型、名目，并深入分析其主要内容、价值及与此相关问题。

一、唐代数学教育概述

隋文帝开皇元年（581年），北周外戚杨坚灭北周建立隋朝，589年灭南朝陈代，完成国家重新统一大业。唐高祖武德元年（618年），在社会内外交困，阶级斗争和民族矛盾尖锐复杂背景下，隋炀帝杨广又被李渊及李世民父子所灭，王朝更替，重新建立唐朝。自西汉末至三国、南北朝时期，数学教育经历了漫长的历程。唐代数学教育在继承前代成就的基础上，取得显著进步。唐代是我国封建社会经济的鼎盛时期，农业、工商业发展壮大。与此同时，伴随着各专科学校的设立而相应确定了相关专门技术的教学内容和知识传播，以满足社会物质生产和现实生活的需要。唐代数学教材促进了数学教育及其他科技教育的实践及专业人才的培养。

隋朝中央官学设有国子学、太学、四门学、书学、算学、律学，但限于立国时间短暂，并未系统化、正规化。唐代中央官学制度由六学二馆组成，六学隶属于最高学府国子监，包括国子学、太学、四门学、律学、书学、算学；二馆包括弘文馆、崇文馆。弘文馆、崇文馆设学士校书郎，既承担负责经籍图书的校对及整理工作，也向学生讲授文化知识。算学是中央官学中“六学”之一，在唐代官学中占有重要地位，也是世界上最早的数学专科学校。唐代数学教育机构曾先后分别设立在西都长安和东都洛阳。算学官学有算学博士2人，招收算学学生30人。算学博士“掌教文武官八品以下及庶人之子为生者”，表明学生来源社会层次及家庭出身都相对较低，比不上儒学官学的学生等级地位显赫。在数学教育中，以《算经十部》等作为数学专业主要教材。

唐代将学校教育与科举考试贯通，实现对接，以实现学校培养与科举选拔的统一。唐代科举考试中，明算作为常科，每年进行。应试者有生徒、乡贡之别，前者是官学毕业生，后者源于私学或耕读传家的自学者，这体现了唐代政府对数学教育的高度重视。明算科考试的内容和方法主要参照官学中算学专科教育。文献作如下记录：

凡算学,录大义本条为问答，明数造术，详明数理，然后为通。试《九章》三条、《海岛》《孙子》《五曹》《张丘建》《夏侯阳》《周髀》《五经算》各一条，十通六，《记遗》《三等数》帖读十得九，为第。试《缀术》《缉古》、录大义为问答者，明数造术，详明术理，无注者合数造术，不失义理，然后为通。《缀术》七条、《缉古》三条，十通六，《记遗》《三等数》帖读十得九，为第。落经者，虽通六，不第。[1]1162

学生参加明算科的考试，若对《海岛算经》《孙子算经》《三等数》等算学教材如数家珍，深谙其理，能详细阐述其中的原理和方法，通过考核后，则可以获得做官的资格。

科举制的发展促进了数学教育的兴盛，而数学教育又为科举选拔人才提供了便利条件，达成了科举的目标和意图。唐代设立数学专科学校、科举考试设置明算科均为世界首创，由此可见唐代数学教育在人类科技教育史上的重要地位。

唐代数学教育发达，不仅州县地方官学重视数学，而且私学授徒讲学盛行。唐玄宗天宝年间（742-755年）全国州县学校学生总数达67 100人，培养了一批数学人才，如王孝通、张遂、韩延、龙受益、江本、陈从运等。唐代私学同样采用《十部算经》为教材，不仅让学生学习系统数学知识，而且钻研新的数学解题方法。三、四次方程的解法以及二次不等间距内插法等都是师生潜心教学的重要内容。唐太史令李淳风家族四代均通晓天文历算。在家庭的耳濡目染之下，李淳风自幼对数学饶有兴趣，从小便“通群书，明步天历算”[2]5798。唐代历象学家僧一行为探寻算术奥秘，跋涉千里向知名学者求教，曾抵达浙江天台山（今属台州市境）国清寺，向隐居在此的僧侣学习算术。僧侣、道士淡泊名利，一心向学，对数学教育的发展起到了重要作用。

佛教是唐代流行的宗教，也是一种宗教私学教育。籍此时对僧一行及佛教数学教育略做扩展和深化。唐代佛学兴盛，南北各地禅宗流派多在名山大川、形胜之地建庙收徒，研修佛经。佛教僧尼，除了在一些寺院尼庵进行佛经研习、佛教教育活动外，也有世俗的知识文化传授，乃至科技内容的研习，突破了宗教教育的羁绊。据《旧唐书·一行传》记载：著名的历算学家一行和尚（俗名张遂），曾在河南嵩山普寂和尚处研习佛典和天文历算知识，后来又到浙江天台山国清寺学数学，亲见“僧于庭布算”的情况。僧一行“寻访算术，不下数千里，知名者往询焉，末至天台山国清寺”。“一行访求师资……至天台山国清寺，见一院，古松十数，门有流水，一行立于门屏间，闻院僧于庭布算声”，一行趋而入，“稽首请法，尽受其术焉”。于是，一行“洞天算、阴阳、推步之学”，为日后完成《大衍历》的制作，打下了牢固的科学基础，自有《大衍历》以来，历家都遵循其格式，并用以教学。

疆土辽阔、经济发达、文化多元使唐王朝有博大胸襟，号称“大唐气象”，这在教育领域表现为学校类型多样，教育内容丰富。唐代数学教育方式多样，教育环境相对宽松，甚至存在数学爱好者自学以及僧侣教学的情形。唐代从中央、地方官学到民间社会私学甚至家学兴起了一股数学热潮。数学的进步给城市规划、水利建设、桥梁建筑、商业贸易等事业带来了科学思想和技术力量支撑。

二、唐代官学数学课程及教材

唐代数学教育虽有不同的类型、层次及方式，但主要以中央官学专门数学教育为主。因此，探讨中央官学专门数学的学科专业课程及教材意义更为突出。需要说明的是课程与教材是现代教学论中带有共生交叉，乃至相当程度互用的概念，无非前者重在资源内容，后者表现为实态文本或媒介。这种情形在唐代数学教材中更为明显。

隋文帝在位时设国子寺，国子寺设有国子、太学、四门、书、算学。数学教育在隋朝时成为一门独立学科，数学教育走向专业化、规范化。唐代在隋代的基础上建立了更加完备的数学教育体系，大学开设数学专业，建立算学官学机构。唐代的数学教育专业化明显，既有严密的教学计划，又有专业的数学教材。

依据《新唐书·选举制》所载：唐代算学官学学制7年，学生共有30名。学生入学年龄从14岁到19岁不等，由算学博士分科教授。算学博士收到学生敬献的丝帛酒肉作为束脩之礼，“掌教文武八品以下及庶人子为生者。二分其经以为之业。习《九章》《海岛》《孙子》《五曹》《张丘建》《夏侯阳》《周髀》，十五人。习《缀术》《辑古》十五人。其《记遗》《三等数》亦兼习之”[1]1160。算学生分为两组，每组15人，每组学习不同的教材，同时学习《数术记遺》和《三等数》。对于学生的学习，制定严密的教学计划：“凡算学：《孙子》《五曹》共限一岁。《九章》《海岛》共三岁。《张丘建》《夏侯阳》各一岁。《周髀》《五经算术》共一岁。《缀术》四岁，《缉古》三岁。《记遗》《三等数》皆兼习之。”[1]1160这种按学习的难易程度和学生的数学基础的分科教学，在古代数学教育史上具有开创性意义。

算学专科学校由国子祭酒管理，管理制度严格。国子监对学生的学习以及学籍情况都有备案记载。学生修完课程后需参加旬考、月考和岁考。考试内容依据教材内容而定，学生毕业后参加科举考试，按照上引文献可知其中的设计：第一组“试（九章）三条《海岛》《孙子》《五曹》《张丘建》《夏候阳》《周髀》《五经算》各一条”，第二组试“《缀术》七条，《辑古》三条”，每组分别10道题。此外还要加试《记遗》《三等数》。考试成绩评定也有明确标准，两组10道题的要求相同，试题“十通六”，“《记遗》《三等数》帖读十得九，为第（及格）”。有时还要进行口试，规定“得八以上为上，得六以上为中，得五以下为下”。考试有明确范围，使学生能够有重点、有主次地进行复习。成绩评定有客观标准。学生的休假时间安排为：每10天放假一次，但放假前要参加一次考试；另外学生享受5月份的“田假”以及9月份的“授衣假”。如果学生违反规定、不服从教师管教、不按时到校、连续3年下第或9年学无所成则开除学籍，不得继续学习。

唐代不仅有完备的数学教学制度，而且有一批专业的算学博士负责教材的讲授工作，如刘孝孙、王孝通、梁述、张元贞等。刘孝孙曾细草《张丘建算经》；梁述曾参与《算经十书》的注释工作；王孝通是唐代有名的数学家，天资聪慧，自幼学习天文历算学，刻苦钻研算术知识，探寻其中的奥秘，用毕生心血完成《缉古算经》。全书共1卷，记录了20个数学问题，主要从求出三次方程的正根、体积计算、勾股定理及工程建设等几个方面介绍了一些算法。书中记录的高次方程解题方法，是中国现存典籍中关于高次方程的最早记述。因其内容深奥，学生学习起来也颇有难度，规定修业年限为3年。此外，《缉古算经》关于三次方程数值的解法为宋元时期天元术和四元术的诞生奠定了坚实的基础。

三、唐代代表性数学教材

限于历史久远而导致古代数学教材留存稀少，搜求不易，要想全面呈现唐代数学教材是难以实现的。以下只对其间的代表性教材进行举例分析，以发挥“弱水三千，但取一瓢”的样本作用。

（一）《算经十书》

唐代专科学校纷纷建立，分科教学发达，数学教育不仅为政府输送一批精于计算的官员，而且促进了天文历法等自然科学的发展。数学教育的实施除了需要德才兼备师资队伍，还需要一批精良的教材。显庆元年（656年）唐高宗命太史令李淳风负责注解《算经十书》，该书是第一套由政府统一审理编订的数学教材。“淳风复与国子监算学博梁述、太学助教王真儒等受诏注《五曹》《孙子》十部算经。”[3]2719《算经十书》注释历时24年，可见时间之长，难度之大。《算经十书》囊括了十部重要数学著作：《九章算术》《海岛算经》《孙子算经》《五曹算经》《张丘建算经》《夏侯阳算经》《周髀算经》《五经算术》《缉古算经》《缀术》。《算经十书》内容丰富多样，被唐代教育机构指定为可传授的数学教材。这不仅有利于数学专门人才的培养，而且在古代数学教材史上具有里程碑意义。

通过对汉代，特别是魏晋南北朝数学教学著作和教材的仔细研读，李淳风等数学家发现其中虽然介绍了许多数学知识和算法，但也存在着一些纰漏和错误。于是，他们对其中存在的问题进行了更正，并研究出了一系列新的数学原理和计算方法。不仅如此，许多面临失传的数学知识也因此而继续保存流传下来。《算经十书》中成就最大的是《九章算术》。该书由西汉数学家张苍、耿寿昌编撰，唐李淳风对其进行了注释。《九章算术》在我国数学教材史上地位突出，标志着中国古代数学体系的形成。

李淳风对开立圆术、配分比例、复比例、等差数列、课分、差分加以注释，对数学有精深的造诣，其中课分、差分的算法与现代一致。李淳风发现《周髀算经》中的日高公式存在问题，以南北相去一千里，日中测量八尺高标竿的影子相差一寸的算法脱离实际，与“盖天说”不符。他冥思苦想，利用已有的数学知识并结合实践经验重新修正，成功地将其转化为平面上一般的日高公式去处理，为中国古代测量术的进步发挥了作用。在《九章算术》的注释中，李淳风引用了南朝数学家祖桓提出的球体积的正确计算公式，即“幂势既同则积不容异”的祖桓定理。祖桓定理原本是由祖冲之、祖桓父子发明，并记录在《缀术》中。不幸的是《缀术》年久失传，因此这一原理最终因李淳风等人的注释得以继续为后人知晓。

中国古代历来重视对古籍的注释，许多典籍都因此流传千古。李淳风等人对《算经十书》进行的全面注释有效保留并传承了唐朝以前的数学知识，在中国数学发展史上具有划时代的贡献，对唐朝以后的数学发展有着不可磨灭的影响。唐代国子监所属算学专科学校之所以能培养一些实用人才，采用具有较高学术水平的专业教材，是一个重要的因素。所以对李淳风等人的历史贡献，还是应该给予肯定。[4]107-108

（二）《九章算术》

科学技术教材是有很强的继承性的。《九章算术》源自汉代，沿用作魏晋南北朝官私学数学教材，又是唐代最具代表性和使用时间最久的数学教材。关于该类数学经典教材的意义及地位，有学者称：“从汉代至清代中叶，其间近2 000年，都采用《九章算术》作为教科书，培育了一代又一代的数学教育工作者和数学大家。祖冲之、王孝通、李淳风、贾宪、杨辉、秦九韶、朱世杰、吴敬、程大位、梅文鼎、戴震、梅瑴成、阮元等，都受到了《九章算术》的启迪，他们的著作，大都是采取《九章算术》应用问题集的形式，展示各自的创造成果，形成了中国独具特色的数学教育传统。”[5]25

1.《九章算术》的内容

中国古代数学专著都是不断总结生活实验成果而成的，《九章算术》也不例外，其内容集中体现了数学知识在生产生活实践中的应用。如《九章算术》的内容虽极为丰富，按算法分为方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股等九章，但这些内容主要关乎农业生产中极具应用价值的数学知识。“方田”是指土地形状，涉及各种形状地亩面积的计算，有包括计算各种形状面积的公式及分数四则运算法则；“粟米”指谷物品种，主要阐释各种谷物交换的比例算法；“衰分”指分配比例，涉及比例分配算法；“少广”指边长问题，包括面积与体积的运算，提出了世界上最早的开平方与开立方程序；“商功”为工程计算，涉及各种体积公式和土方工程工作量的分配算法；“均输”意为平均输送，包括人口多少、路途远近、谷物贵贱和赋税负担的运算方法；“盈不足”是盈不足术的代称，涉及盈亏类问题的算法；“方程”指方程术，涉及当今数学中的线性方程组解法等；“勾股”指直角三角形，涉及直角三角形的理论。

另外，在实践应用的基础上，《九章算术》含有近百条十分抽象的术文，即公式、解法以及246道例题。其中分数理论、比例和比例分配、盈不足、开方等算法、线性方程组解法、正负数加减法则、解勾股形方法等都超前其他文化传统几百年甚至千余年，是具有世界意义的重大成就。[6]5

《九章算术》采用以应用问题集的形式加以组织，按照问题的性质进行大的分类，形成章节，每一类为一章节。再依照问题的解法（《九章算术》中称为“术”）进行具体分类，形成每一章节的多个小类。每一小类都有解题步骤，包括数学公式、推理等。这种结构体系，是以算法为中心，根据算法组建理论体系。依此编纂体例，《九章算术》全书246个问题被分为9类，每一类为1章，全书共9章。每一类问题的解析通过例题、答案和术来演示，依照术的不同，每一章的问题又进一步被分为不同的小类。如一术解一题的类型，以勾股章的一题为例：“今有圆材径二尺五寸，欲为方版，令厚七寸。问：广几何？答：二尺四寸。术曰：令径二尺五寸自乘，以七寸自乘减之，其余，开方除之，即广。”[7]410这种类型中术文只适用于该题目，可以说是一术一题，具体的术解析具体的题目。《九章算术》衰分、均输、勾股等章的部分题目采用了此编纂体例；一术解一类题的类型，即一类问题只有唯一术文解析，术文抽象、严谨且具有普适性，而每一题只有题目和答案，不再有术文。《九章算术》方田一章的“今有田广十五步，纵十六步。问：为田几何？答曰：一亩。又有田广十二步，纵十四步。问：为田几何？答曰：一百六十八步。术曰：广纵步数相乘得积步。”[7]9就是这种类型。两例题都只有题目和答案，两例题后的术文是对两例题的共同解析。当然这种类型的具体形式还可以多样，除了上面的先题后术的形式，还可以先术后题，一题一答。如《九章算术》商功一章有关“城、垣、堤、沟、堑、渠”面积计算的例题及术文：“术曰：并上下广而半之，以高若深乘之，又以袤乘之，即积尺。今有城，下广四丈，上广二丈，高五丈，袤一百二十六丈五尺。问：积几何？答曰：一百八十九万七千五百尺。”[7]176就是这一形式。也可以先总术后例题，每道例题一题一答再分术。这种编纂形式是先给出抽象的总术，再列举多道例题，但和第二种编纂形式不同之处在于每道例题除题目和答案外还分别都有一条具体术文，阐释总术在本例题中的具体应用方法。《九章算术》粟米一章的一题“术曰：以所有数乘所求率为实，以所有率为法。今有粟二斗一升，欲为粺米。问：得几何？答曰：为粺米一斗一升五十分升之十七。术曰：以粟求粺米，二十七之，五十而一”[7]70-71。就采用了这种编纂形式。

数学教材的编写紧密结合当时的社会生活实况。汉代社会至今已年代久远，而今要了解汉代的历史，除了翻阅文献典籍之外，《九章算术》可以说更生动地记录了汉代社会经济状况，涉及了汉代人日常生活的方方面面，它用一个个数字，一道道例题清晰地解读了汉朝百姓的衣食住行、柴米油盐。“今有人共买琎。人初半，盈四，人出少半，不足三。问：人数、琎价各几何？答曰：四十二 人，琎价十七。”[7]308这一例题例题证明汉代已经有了“团购”。“今有人持米出三关，外关三取一，中关五而取一，内关七而取一，余米五斗。问：本持米几何？答曰：十斗九升八分升之三。”[7]259这一例题则记录了汉代税务计算。“今有素一匹一丈，价值六百二十五。今有钱五百，问：得素几何？答曰：得素一匹。”[7]113这一例题记录了汉代物价情况。这一道道的例题使千百年前的汉代社会不再虚无缥缈。

四、唐代数学教材的特点及其影响因素

唐朝政府对数学教育中教学内容设计及编选给予重视，数学教材呈现出实用性、直观性、趣味性并存的特点。唐代数学教材为后世数学教育的发展打下了坚实的基础，促进了数学教育的逐渐走向成熟。通过教育政策主流思想和制约数学教育活动的科举制度等因素分析，可以深刻解读唐代的数学教材。

（一）唐代数学教材的特点

通过对唐代数学教材的总体认识及具体分析，得出唐代数学教材有如下特点：

1.实用性：指向问题的解决

唐代地域辽阔，土地宽广。为巩固统治，统治者实行均田制分配土地，以租庸调制获取税收。均田制和租庸调制的实施要求土地丈量以及谷物、布匹征收的准确，农民土地的分配要做到均等、赋税征收的计量都需要数学的计算，由此带动了数学的发展。出现了不少注重实用性问题解决的数学教材。

《九章算术》作为唐代学习数学的专业教材，内容十分丰富，包含246个数学应用问题，并为每道题配有详细的答案。按问题性质和解法不同分为方田、粟米、衰分、少广、商功、均输、盈不足、方程及勾股等9个章节。《九章算术》注重问题解决，将理论与实际结合，对生产问题的解决有促进作用，体现了数学思想与实际应用完美的结合。

现有大量的研究针对“社工+义工”合作模式路径提出了一系列可行性的路径：政府体制转轨、政策法规建设、社工自身队伍建设、义工管理制度、民间组织培育、建立信息资源共享平台等。在新常态下，社工与义工联动面临新的机遇和挑战，而社会资本视角有利于探讨以社区为本的“社工+义工”联动模式治理的新路径。

《五曹算经》是北周数学家甄鸾潜心编撰的数学著作，受到历朝数学家的追捧，出现了许多刊印版，唐代时被指定为官方数学教材。全书共5卷，分别为田曹、兵曹、集曹、仓曹、金曹。唐代施行均田制，土地的丈量需要更加精准。“田曹”讨论了各种不同形状田亩面积计算方法；“兵曹”介绍军队给养问题；“集曹”对粟米互换问题进行了阐述；“仓曹”对租税和仓储容积的计算给予详细描述；“金曹”主要记载户调的丝帛以及物品贸易。《五曹算经》对生产生活中迫切需要的数学问题进行了介绍，阐述了现实生活中各项问题的计算方法，具体问题具体分析，实用性突出。

2.直观性：数图结合的体例

唐代数学教材不仅重视理论与实践的结合，而且对体例较为注重。数学教材摆脱了长篇文字的枯燥，穿插生动形象的图片，照顾到学生的学习体验，直观性明显。

《海岛算经》是魏晋时期刘徽所编的一部测量数学著作，唐代被列为数学专科教材，供算学馆学生上课使用。全书共包含9个数学问题，每题的问题、答案及算法详细，涉及里、丈、步、尺、寸等长度单位。9个问题分别为：测望海岛、测望山上松高、南望方邑、俯测深谷、登山望楼、遥望波口、下望深渊、登山望津、测邑广长。《海岛算经》有许多新奇的数学计算方法，如“重表法”“连索法”“累矩法”等，这些方法为测量工作带来了极大便利，也为地图学奠定了基础。《海岛算经》中的插图形象表达了勾股定理的运用。

《周髀算经》作为《算经十书》之一，被唐代列为明算科教材。书中详细介绍了勾股定理、盖天说和四分历法等问题。《周髀算经》中的数学计算已使用分数法和开平方法等难度颇大的计算方法。《周髀算经》中的“弦图”也形象地论证了勾股定理的使用。

3.趣味性：通俗易懂的表述

唐代数学教材内容丰富，独具特色，设计精良，不仅与生产劳动相结合，直观性与现实性相结合，而且趣味性强、通俗易懂。《张丘建算经》是北魏数学家张丘建编撰的教材，也是唐代重要的数学教材之一。书中共包括92个问题，介绍了最大公约数、最小公约数、等差级数及二次方程等问题。其中关于百鸡问题的解法最为独特：今有鸡翁一，值钱五；鸡母一，值钱三；鸡维三，值钱一。凡百钱买鸡百只，问鸡翁母维各几何。该题对不定方程的解法堪称中国最早。书中采用朗朗上口的歌诀形式对百鸡问题进行了阐述，简明易懂，便于理解。百鸡问题因简单明了、趣味十足的阐述形式而流传至今。

（二）唐代数学教材的影响因素

唐代数学教材的变迁是传统教育变迁的缩影，中国传统教育是在封建社会主导教育思想即儒家教育思想影响下变化发展的，唐代数学教材的变迁也深受儒家“经世致用”思想的浸润。同时，教育制度，尤其是封建科举制度作为传统教育的指挥棒对数学教育及教材也产生了非常重要的影响。

1.儒家“经世致用”思想使唐代数学教材凸显实用性

“经世致用”是中国传统数学教育和教材内容编写的指导思想。如汉代，奉行“罢黜百家，独尊儒术”的文教政策，使教育呈现了儒学化。其中最突出表现就是经学教育在此后近两千年的传统教育中占据着主导地位。“独尊儒术”对数学教育发挥了明显导向作用，儒学讲究“经世致用”，学习知识是为了解决实践问题。在这一思想指导下，数学教育的思想、内容、方法向着实用价值的方向转移，从社会生产和日常生活的需要中产生问题并为社会生产和生活服务。中国社会自古就是农业经济社会，农业与手工业生产是社会主要的经济活动，数学教育的内容也相应以应用于农业生产实践的数学知识为主，如表1所归纳《九章算术》的内容所示：

从表1可见，《九章算术》所涉及的内容主要是社会生产及生活应用领域的数学知识或数学模型，涵盖了土地丈量、粮食分配、赋税缴纳、面积与体积计算、土方工程、谷物运输等社会生产生活各方面的数学应用。唐代数学教材除《九章算术》之外，还采用《周髀算经》《孙子算经》《五曹算经》《夏侯阳算经》《张丘建算经》《海岛算经》《五经算术》《缀术》《缉古算经》等数学著作。这些教材的内容也多反映了当时科技和经济发展对数学知识的迫切需要。如《夏侯阳算经》共3卷，收录83个问题，大多数问题都是来自于社会经济活动，为地方官吏和广大百姓解决经济问题提供适用的数学知识和计算技术，体现了生产生活实践对实用数学的需要。由此可见中国古代数学教育与教材受儒学“经世致用”思想影响而服务与应用于社会生产生活实践的应用性特征。

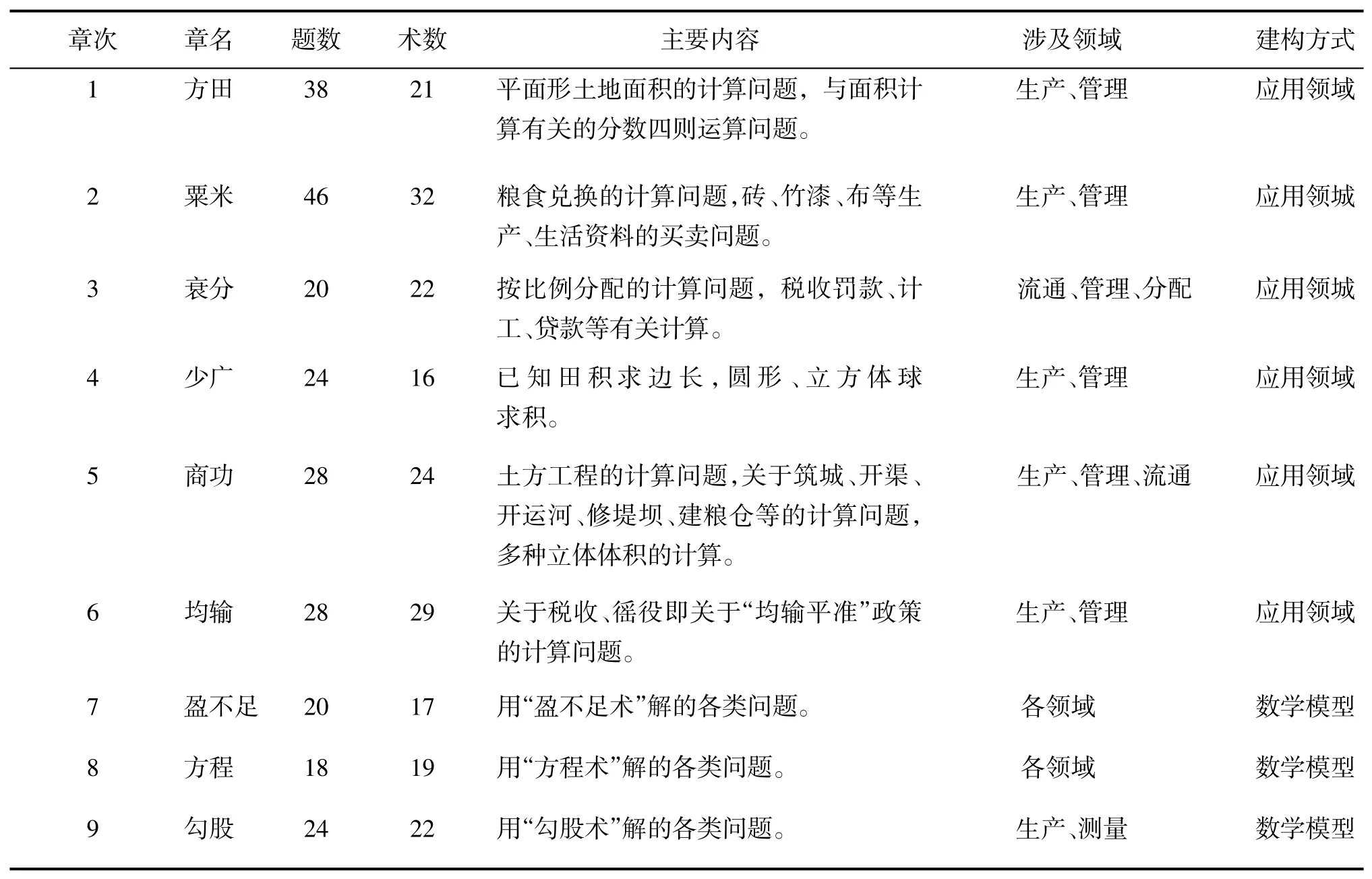
表1 《九章算术》内容一览表[5]24

2.科举制度影响唐代数学教材的设计

隋代确立了科举考试制度之后，科举制度在中国传统社会愈加完善，并逐渐成为中国传统教育的指挥棒，科举考试考什么，官学、私学、书院几乎就教什么。数学教育是具体学科的教育，因而教育制度对其有更为直接的影响，科举考试制度所规定的内容可以说决定了数学教育的形式及教学内容。如唐代的科举制分常科和制科，常科为每年举行的考试，其中就设有明算科。明算科的内容与官学中数学专科教育机构考试一样，考试以明数造术、详明术理为标准，以问答的形式考核教材的基本内容。如第一个专业选《九章算术》中的任意3题，其他教材各任意1题，共10题进行考试，答对6题以上为及格；第二个专业选《缀术》中的任意7题，《缉古算经》中的任意3题进行考试，答对6题以上为及格。另外，以帖经的形式考《数术记遗》和《三等数》，帖10题对9题为及格。考生问答和帖经都及格就可以及第授官。正因为科举明算科对考试内容和形式如此明确的规定和设置，唐代国子监以及地方官学和私学才不仅非常重视数学教育，同时严格围绕科举考试组织教学，将科举考试指定的教材进行了统一编纂，完成中国数学教育史上最具代表性，也是最完善的一整套教材——《算经十书》。《算经十书》可以说是在明算科科举的指挥棒下，专门为科举考试量身定做的一套数学教材，既是对之前数学教育成果的总结，也为后来数学教育的发展完善提供了保障，从唐到五代，300多年间一直有明算科举，每年要有若干生徒和乡贡考数学，“后唐天成五年（公元930年），宋延美明算科及第；是年明算五人，而延美为之首。天成五年二月，改元长兴。长兴元年（公元930年）夏四月，国子司业张溥请复国子学八馆，广揽生徒，以兴绝学，而算学居其一”[8]202。由此可知，明算科的科举考试，促进了唐代数学教材的普及和发展。

令人遗憾的是明清时期，盛行以八股文取仕为特征的科举考试，强调程朱理学，“四书”地位提高，超越“五经”，逐渐取消了数学应试内容，传统数学教育和教材编纂呈现衰微。明代，出于封建专制集权政治的需要，特别强调培养忠君的文臣，加强思想控制，科举考试内容逐渐取消了算学。因此，明代官学国子监不再设算学，讲授《易》《诗》《书》《春秋》《礼记》《大学》《中庸》《论语》《孟子》的“四书”等教材。地方官学虽然兼习数学，但只是启蒙的“六艺”之一。清代前期，文教政策沿袭明代，从巩固中央集权的君主制出发，尊经崇儒，注重程朱理学，严格学制，继续推行八股取士，八股进一步教条化，突出训练时文制艺的格式和体裁技巧，并大兴文字狱，颁行《圣训广谕》，粗暴地扼杀一切新思想，数学教育也受到很大压抑。只是由于西方数学的传入，清代前期开始了中西数学融合的过程，更由于康熙等皇帝的重视，数学教育较明代才有了较大的提升。

五、唐代数学教材的历史评价

唐代重视数学教育，设立专门的数学教育机构，同时在民间及家学中不同程度地进行数学教育以及数学专业人才的培养。数学教育制度为数学教材的编写、注释以及使用提供了保障依托及前提条件；品质精良、数量丰富的数学教材又促进了数学教育的有效开展以及数学专业人才培养目标的达成。

（一）唐代数学教材的地位

中国的数学教育萌芽较早，奴隶社会殷商国学教育就曾出现“书计”的学习，但唐代之前数学教育均无系统的专业数学教材。唐代对以前的数学典籍进行系统总结，组织大批数学专业人才对《算经十书》进行注释，同时这也标志着以《九章算术》为中心的古代数学体系的基本形成，开创了我国数学教材的新纪元。正是由于李淳风等数学家不辞辛劳、日夜整理数量庞大的算术古籍，才使得千百年间的珍贵数学知识得以保存。《算经十书》不仅成为唐朝数学教育的官方教材，而且出现了许多刻本和抄本，在宋、明、清时期大为盛行。《黄帝九章算法细草》《九章算术纂类》以及《数书九章》等数学用书都对《算经十书》的算法进行了深刻讨论，并在此基础上发现了新的数理方法。当代数学中分子、分母、幂、积、开平方、开立方、正、负、方程等数学专业名词和术语也都来自于《算经十书》，可见《算经十书》影响之长久、之深远。

唐代的数学教材中《算经十书》的知识循序渐进具有层次性系统性，基础知识和高难度知识并存。其中《九章算术》《缀术》中的数学知识较为高深，难度颇大；《孙子算经》《五曹算经》则是基础的数学教材。唐代官学数学教育甚至分两个班进行教学的层次组织变化方式开展差异性实验。两班学习的教材略有差别，有的班级学习基础简单的数学知识，有的班级则采用难度较大的教材学习有深度的内容。依据学生掌握水平的不同而采用差异性的教材，不仅可以使学生更好地掌握相关知识，而且便于教师因材施教。

（二）唐代数学教材传播海外

唐代数学教育发达，存在丰富多样的数学教学活动。数学教育实践必须依托种类多样的数学教材，唐代数学教材以《算经十部》为主。数学教材对中国古代数学专门人才培养发挥重要作用，并对世界数学教育史有一定的辐射影响。

唐代数学教材不仅深刻影响了中国数学教育的发展，而且传播到东亚甚至欧洲等国。朝鲜与唐王朝交流密切，商贸及文化往来频繁，曾多次派遣使节和学生前往唐朝。717年朝鲜效仿唐制，设立算学科，置算学博士及助教各1名，讲授《缀经》《三开》《九章》《六章》等数学教材。唐武周长安二年（702年）日本建立学校，开设算术课，教学及考试方法基本仿照唐朝，置算学生1名，算学博士教授《孙子算经》《五曹算经》《九章算术》《海岛算经》《缀术》《周髀算经》《六章》《三开重差》《重开》《九司》等数学专门教材。唐朝与印度交流密切，许多印度天文学家曾在唐朝司天监担任官职，这也促进了两朝之间的数学交流。开元六年（718年），在唐玄宗的号召下，天文学家瞿昙悉达对印度的《九执历》进行了翻译，并且编辑了120卷的《开元占经》。《开元占经》中着重介绍了数码、圆弧度量法和弧的正弦等数学专业知识。《算经十书》成为朝鲜和日本进行数学教育的主要参考典籍，其所用数学教材大多源于此。《算经十书》的影响不仅停留在中亚及印度，更闻名欧洲各国，“于是欧洲人一方面恢复已经失去了希腊数学，一方面吸收有生力量的中国数学，近代数学才得以开始发展”[9]。

（三）唐代数学教材的现实意义

综上所述，唐朝封建社会经济繁荣，自然科学有了很大的发展，数学、医学、天文历法等取得了重大的成果。在古代社会，天文和数学有着密切联系。天文历法的编撰离不开数学方法的支撑，而天文历法的进步又促进着数学教育的继续发展。在历法丛书《大衍历》的编撰过程中，唐代科学家僧一行融入了许多精巧细密的数学计算方法，如不等间距二次内插法、准正切函数表和五星行度计算法。

唐代数学教育经验性与实用性并存，不论是李淳风等数学家对《算经十书》的详细注解，还是僧一行使用的计算方法，均为解决生产生活中的实际问题做出了重要贡献。唐代数学教材的编辑、修订工作，依靠数学家们的亲身实践经验得以顺利完成，对数学教材的钻研和学习最终也是为了解决现实生活中出现的实际问题。数学问题归根到底为数量计算思想和方法，唐代数学教材为后世数学教材的编写及数学教育实践作出了重要贡献。