基于博弈交叉效率DEA模型的中国工业生态效率评价研究*

□ 翟丹妮，于 尧

(南京邮电大学 管理学院,南京 210003)

1 文献综述

生态效率是指生态资源满足人类需要的效率，旨在在环境保护和经济发展之间寻找一个平衡点，有很多学者在生态效率方面做出了很多研究，首先从竞争合作的角度来看，很多研究忽略了通常存在的竞争因素。市场改革开放后，由于区域和市场的分割，相邻区域之间的竞争很容易产生。尽管竞争促进了经济发展，但也导致了重复建设、产能过剩和严重的环境污染[3]。随着城市化进程的推进，各地区人口、资源、环境之间的竞争将更加激烈。因此，竞争关系不容忽视，尤其是在生态效率方面，它连接着经济、能源和环境。因此，需要在工业效率评价过程中考虑环境和竞争因素。

已有的对于生态效率的测算和评价方面的，主要包括集中研究方法，如比值法、指标体系法、生态足迹法、能值分析法、物质流分析法等。孟庆雷等[1]根据生态效率的定义给出了生态效益指标值的测算公式，并建立了固定效应面板数据模型来分析FDI对我国区域工业生态效率的影响。王震、石磊等[2]运用生命周期法，通过清单分析法、当量法、目标分析法等构建了评价指标体系，对北京市工业生态效率进行评价。黄晓杏、王锐[3]运用能值分析法对2009-2018年江西省的矿业城市工业生态效率进行动态分析。此外，随机前沿模型(SFA)也被广泛应用于效率测度，但该模型需要事先确定生产函数的形式，且期望产出变量具有唯一性，难以解决多投入多产出的问题。而DEA 方法作为一种非参数评估方法，在用于多输入、多产出的多目标决策时，无须预先估计参数，从而避免主观因素影响，在简化算法、减少误差等方面有着巨大的优越性，因此本文选择使用DEA方法来进行效率评价。

对于工业生态效率的研究主要涉及行业、企业和区域三个层面。在工业行业方面Liu等[4]以我国工业行业36个部门作为研究对象，将工业生产排放过程看做先排放后治理的过程，运用两阶段网络DEA模型对我国工业生态效率进行评价。Wang等[5]运用混合超效率DEA模型以及Malmquist指数对我国22个工业部门生态效率进行评价。袁宝龙、张坤[6]运用超效率DEA模型对我国制造业28个部门的生态效率进行评价、结果表明我国制造业效率处于低效率但是逐年递增的状态。工业企业方面，赵爽和刘红[7]运用DEA和SFA相结合的方法对我国30个省份工业企业的生态效率进行评价，结果表明工业企业的生态效率会受到污染物治理投资、政府环境规制等因素的影响。张辽等[8]为了测度工业企业真实的绿色技术创新效率水平，构建了基于非径向、非角度包含非期望产出的三阶段SBM-DEA模型对2003-2017年我国30个省份工业企业的绿色技术创新效率进行评估，结果表明，部分地区企业虽具有进行绿色技术创新的意愿，但是效率结果仍然不乐观，效率值虽呈现上升趋势但总体水平较低。在区域方面，张欣[9]运用DEA模型以及Malmquist指数对粤港澳大湾区9个主要工业城市的生态效率进行动静态结合分析。陈杰、王建民、范玉环[10]运用超效率SBM和Malmquist指数模型对长江经济带9省2市2010-2017年的工业生态效率分别进行静态效率评价和动态效率评价，并运用Tobit回归分析工业生态效率的影响因素，结果表明各省市效率差异明显，技术进步是工业生态效率提升的主要原因。

很多学者采用DEA方法进行效率评价，但在评价对象的关系方面，传统的DEA方法无法评估DMU之间存在竞争关系的情况，可能会使评价结果与现实情况不符，该问题可通过博弈模型解决；在评价基准方面，交叉效率模型去除了传统DEA模型自评的缺点，结合同行评价，使得结果更具有公信力和可比性；但是交叉效率存在一个被广泛探讨的问题：DEA交叉效率的评价结果通常不是帕累托最优的，针对此问题，很多学者进行了研究和应用，Wu等[11]运用博弈交叉效率分析奥运会奖牌产出效率。Ang等[12]将酒店按品牌进行分组，运用组群博弈交叉效率模型对台湾地区酒店业的运营效率进行分析。Chen等[13]运用博弈交叉效率DEA 测量环境约束下的我国电能效率，研究表明，我国东部地区的能源效率远远高于中西部地区。此外，博弈交叉效率存在生成的决策单元平均交叉效率分数可能不是帕累托最优的问题，Wu等[14]为获得帕累托最优的效率结果，提出了一种帕累托最优检验模型和改进模型。因此，考虑到各省份之间的竞争关系，为了获得能够被所有决策单元接受的效率评价结果，本文借鉴Wu等提出的模型，对中国工业生态效率进行评价。

2 研究方法

本章主要对于交叉效率模型和基于帕累托最优交叉效率模型进行介绍。

2.1 交叉效率模型

DEA(数据包络分析)模型是一种非预先设置参数的评价方法，主要思想是为每一个决策单元提供一个最优的权重集，以最大化其加权输出总和与加权输入之和的比率，该效率值不大于1(个别模型除外)。效率值等于1时，则说明该DMU有效，效率值小于1时，则说明该DMU无效，效率仍然有待提高。Charnes,Cooper和Rhodes[15]首次提出CCR模型，实现了对DMU有效性的评价，具体的CCR模型如式(1)所示：

假设任一决策单元DMUj，j=1,2...,n，有m个投入，s个产出，投入xij(i=1,2,...,m；j=1,2,...,n)表示第j个DMU的第i个投入，产出yrj(r=1,2,...,s；j=1,2,...,n)表示第j个DMU的第r个产出，设则CCR模型为

vid,urd≥0,r=1,…,s；i=1,…,m

(1)

Edd为DMUd的效率值，其中urd和vid是DMUd选择的乘数，用于计算DMUd的效率，不同的DMU可能会选择不同的urd和vid来衡量效率，这使得结果不可比较，而交叉评估的概念使用n个DMU选择的乘数来计算交叉效率，并使用平均值作为最终效率衡量，从而使结果具有可比性。假设用Edk表示从DMUd选择的乘数计算出的DMUk的效率，那么计算公式如(2)所示：

(2)

那么就会形成一个交叉效率矩阵，具体矩阵如式(3)所示：

(3)

对角线上的效率值即为DMU的传统CCR效率值，第k列效值率的平均值则为DMUk的最终交叉效率值，DMUk的最终交叉效率值Ek的计算如公式(4)所示：

(4)

2.2 基于帕累托最优交叉效率模型

Wu提出的帕累托最优交叉效率模型包括两个部分，第一部分是帕累托最优检验模型，第二部分为帕累托最优改进模型，帕累托最优检验模型如式(5)所示。

MinZd

s.t.VdXd=1

UdYd≥θd

VdXj-UdYj≥0(j=1,2,…,n)

Ud≥0

Vd≥0

(5)

式(5)中θ={θ1,,θ2,…,θn}为给定的初始交叉效率值，即式(5)测得的效率值。

通过使用帕累托最优估计模型，可以确定决策单元是否有潜力在不降低任何决策单元交叉效率得分的情况下提高自身交叉效率得分。为了对非帕累托最优交叉效率决策单元的交叉效率得分进行帕累托改进，Wu提出了帕累托最优性改进模型，如式(6)所示：

Vd≥0

Ud≥0

(6)

(7)

3 实证分析

上文已经对相关的理论和分析方法进行了详细的阐述，后面则会将上文中提到的模型应用于具体的数据中，对其效率得分进行具体分析。

3.1 指标选取

考虑到数据的可获取性和分析结果在时间维度的可视性，本文选取2014-2018年除西藏、香港、澳门的30个省、自治区及直辖市为分析对象。相关数据来源于历年的《中国能源统计年鉴》《中国环境统计年鉴》以及各省历年统计年鉴。

生态效率的基本思想是最大化价值，因此仅从投入产出的含义来判断投入产出指标是不合理的，就本题而言，污染物产出属于非期望产出，应最大限度地减少资源消耗和环境污染，或者从成本和收益的角度出发，将污染物和资源的消耗看作是获取经济发展的成本，这与DEA方法所要求的投入产出指标相一致，因此本文选择工业能源消耗、废气排放、废水排放和固体废物产生量为投入指标，工业增加值为产出指标。由于各个省市的指标计算标准和单位有所不同，为了结果的可比较性，本文运用一下公式作为非期望产出的计算标准：废气排放=工业二氧化硫排放总量+工业氮氧化物排放总量+工业烟尘排放总量；废水排放=工业化学需氧量排放总量+工业氨氮排放总量；固体废物排放量=一般工业固体废物产生量。在能源消费指标的收集方面，由于各省的能源消费种类不同，能源消费选取工业原煤原油及其制品、天然气和电力作为能源投入。具体的指标体系如表1所示。

表1 工业生态效率评价指标体系

3.2 结果分析与讨论

运用上一章中构建的帕累托最优交叉效率对2014-2018年我国30个省市自治区工业生态效率进行分析，具体的效率得分如表2所示。

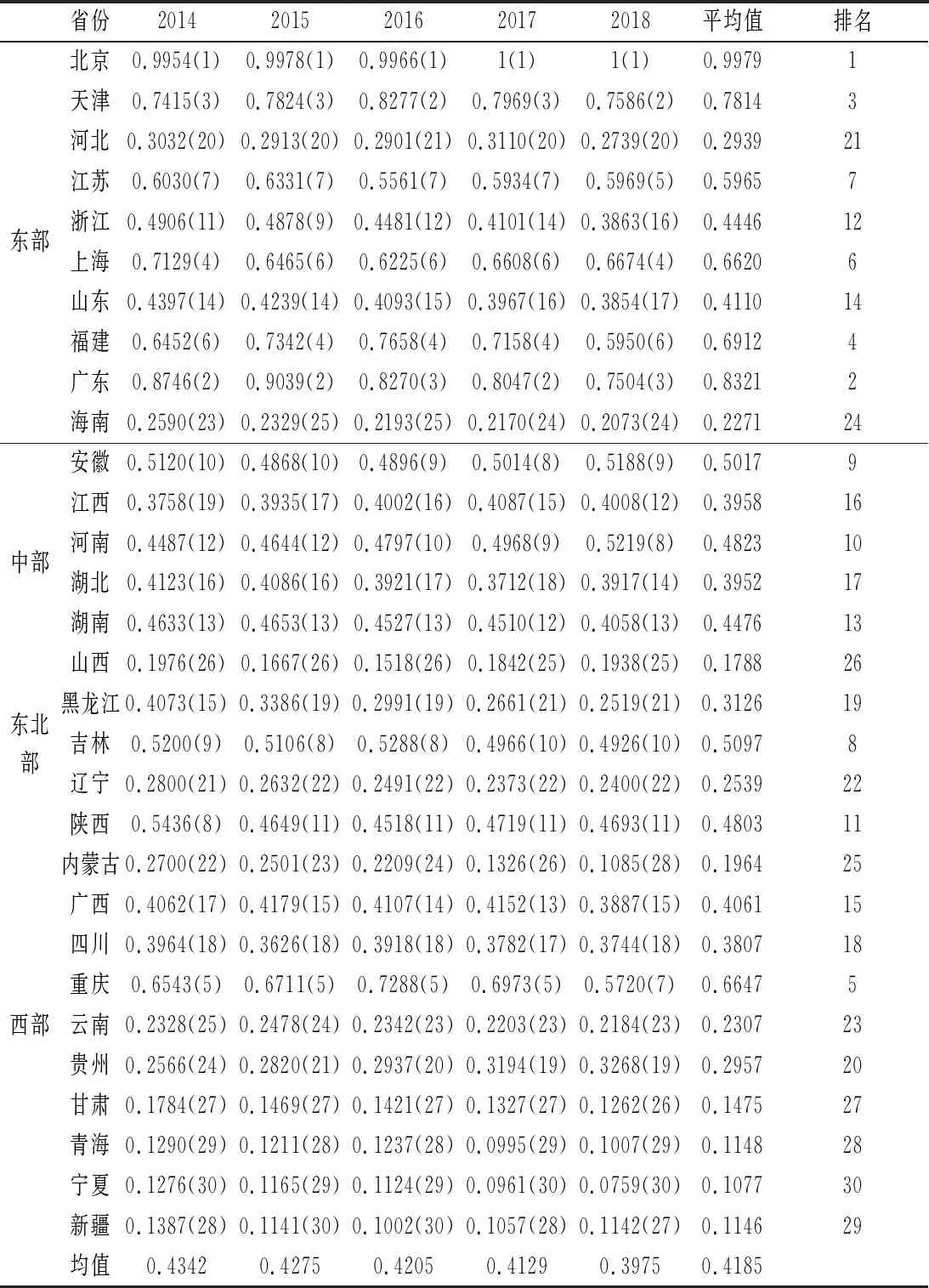
表2 帕累托最优交叉效率得分

从全国总体来看，我国的平均工业生态效率仅有0.4185，省份间的工业生态效率也还有明显的差距，大部分地区的生态效率具有很大的提升空间。从2014-2018年平均水平来看，有13个省份的平均效率值高于全国平均效率值，包括北京市、广东省、天津市、上海市、福建省、重庆市、江苏省、吉林省、河南省、安徽省、陕西省、湖南省、浙江省。效率排名靠前的六个地区分别为：北京市、广东省、天津市、福建省、重庆市、上海市，其中有五个地区位于东部，且该五个地区在2014-2018五年间每年的效率排名皆处于前六名，效率值排名靠后的六个地区分别为宁夏、新疆、青海省、甘肃省、山西省、内蒙古，除山西省外其余五个地区位于西部，其中，青海、宁夏和新疆在五年间每年的效率排名皆处于最后三名。该结果更能够体现出地区工业生态效率值高低与经济发展水平有明显的相关性。其中，北京市、广东省、天津市、上海市、福建省、重庆市五年间的工业生态效率值皆高于全国平均水平，且该六个省市中有五个属于东部地区。平均效率排名最后六个省市包括内蒙古、山西省、甘肃省、新疆省、青海省、宁夏，且该五个地区在五年间皆处于工业生态效率的最低水平。

①六种波动类型。

根据各地区的效率波动情况可以分为六种类型：平稳型、波动型、先下降后上升型、先上升后下降型、上升型和下降型六种，各类型中包含的省份如表3所示。以福建省、贵州省、黑龙江省、江苏省、青海省为例(分别属于六种类型之一)的效率变化趋势如图1所示。

表3 六种波动类型

图1 效率变化趋势图

平稳型地区包括北京市、广西省、安徽省、青海省、云南省，说明该五个省自治区的效率值在2014-2018这五年间保持较为稳定，并没有明显的效率值变动，变动保持在0.03的范围内。波动型地区包括湖北省、四川省、河北省、吉林省、陕西省和江苏省六个地区，其中，湖北省和江苏省的变动趋势呈“N”字型，即呈“上升-下降-上升”趋势，四川省、吉林省和河北省则均呈现“倒N”的变动趋势，即“下降-上升-下降”。先下降后上升型包括上海市、山西省、新疆、辽宁省四个地区，其中上海市、山西省、新疆的效率最低值皆位于2016年。下降型包括内蒙古、甘肃省、宁夏、黑龙江省、浙江省、海南省、山东省。上升型地区包括河南省和贵州省。先上升后下降型包括广东省、天津市、福建省、重庆市、湖南省、江西省六个地区。从各省市五年间的效率波动情况来看，浙江省、江西省、黑龙江省和内蒙古的排名波动较为明显，其最低名次与最高名次之间的差距分别为7、7、6、6，其余省份的排名则较为稳定。

②区域分析。

2014-2018年我国东部、东北部、中部、西部四个区域的工业生态效率如表4所示。

表4 我国区域工业生态效率

我国东中西以及东北部地区生态效率的变化情况如图2所示。从效率值的变化趋势来看，各地区自身的效率变化趋势较为平稳，但地区之间存在较大差异，东部地区生态效率明显高于其他地区，在0.45-0.6之间波动，中部地区次之，效率水平处于0.3-0.4中间，西部地区的工业生态效率则处于最低水平，效率水平处于0.2-0.3中间。根据分析可知，工业生态效率区域间发展水平严重不均，东部地区与其他效率低下地区的差距并没有缩小的趋势。

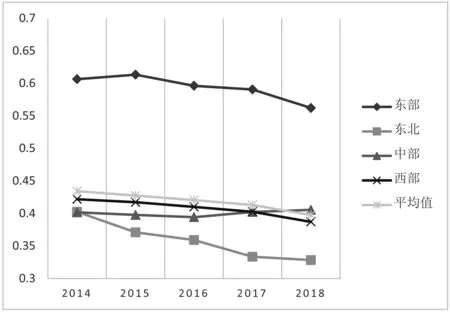
图2 各地区生态效率变化情况

4 总结

基于上述的工业生态效率和区域进步水平的评价结果与分析，本文提出以下建议：

①目前中国正处于经济战略转型关键时期，实现工业的绿色发展应该成为每个地区共同的责任。我国地域广大，各地的地貌、气候、文化、经济水平等不近相同，导致了不同地区的工业生态效率水平差异较大，出现两极化现象。一方面各地区应当增强提高工业生态效率的意识，根据自身实际情况，并结合行业和环境的差异来制定适合自身提升工业生态效率的政策措施，实现工业的绿色发展。另一方面，应该加强地区间的经验交流与合作，缩小各个地区间的差距，发挥相邻地区间的辐射作用。具体来说，根据上文的分析可知，东部地区在工业生态效率方面具有绝对优势，因此东部地区应当充分发挥辐射带头作用，将丰富的绿色生产经验、先进的绿色技术和设备、优秀的管理和研发人才以及雄厚的资金支持进行跨区域输送，提高其他地区效率，以此缩小区域间差距。工业生态效率值低的地区也要积极加强与东部地区的交流沟通。

②政府把重点放在节约能源消耗和清洁生产上，加大研发力度，鼓励工业企业技术创新。各地区应提供更多的资金支持和研发优惠政策，将技术转化为生产力。企业也要把科学技术作为第一生产力，把经济效益和生态效益统一起来。其次，政府作为规划者、管理者和服务提供者，应发挥支持作用，致力于解决经济、能源和环境冲突。首先，政府应加大对工业污染物治理的投入。其次，政府应加强对工业污染物的监管，建立有效的环境评价体系，确保投入资金的绩效。最后，政府应通过宣传教育引导人们树立环境意识。