2-D T-S模糊时滞系统状态反馈H∞控制
彭 丹,陈 莹
(燕山大学 理学院,河北 秦皇岛 066004)
0 引言
二维(two-dimensional,2-D)系统由于在热处理、多维数字滤波和迭代学习控制等方面的大量应用而被广泛地关注[1-5]。一般来说,2-D系统的基本理论被视为传统一维(one-dimensional,1-D)系统理论的推广。但是使用传统的1-D系统理论不能对2-D系统进行分析,因为1-D系统和2-D系统之间存在深刻而实质性的差异,2-D系统信息传播沿着水平和竖直两个方向。此外,研究实际问题时,还需对系统进行控制,如滑模控制[6]、采样控制[7]和H∞控制[8]等。
在对实际现象进行建模时,实际系统往往是一个复杂的非线性系统[9-12],近年来,模糊理论在2-D系统中取得了重要发展。文献[13]讨论了2-D Takagi-Sugeno (T-S)模糊系统的故障检测观测器设计问题。文献[14]利用Lyapunov-Krasovskii函数(Lyapunov-Krasovskii function,LKF),给出了以线性矩阵不等式(linear matrix inequality,LMI)的形式保证2-D T-S模糊系统渐近稳定的充分条件。文献[15]重点研究了2-D T-S模糊系统输出反馈滑模控制的问题。虽然模糊理论已经应用于2-D系统,但在现有的2-D模糊系统中,与研究不含时滞[16]系统的文章相比,研究含有时滞系统的文章数量偏少。工程系统对外部信号的响应绝不是瞬时的,并且总是受到时间延迟的影响。在延时的情况下,系统的性能通常是不可预测的,甚至是混乱的。因此,研究时滞系统的稳定性分析是控制工程领域的一个重要课题[17]。虽然2-D模型被广泛应用,但2-D T-S模糊时滞系统的理论还远未发展,因此,研究2-D T-S模糊时滞系统非常重要。
目前,提高系统稳定性标准有两个重要手段。第1个是LKF的选择,第2个是LKF的前向差分的估计。正如文献[18]所讨论的那样,使用分段的LKF可以降低保守性,获得更好的结果。然而,基于柯西矩阵不等式和松弛矩阵变量的方法不仅在可行性上是保守的,而且还会产生计算负担。文献[19]提出了一种新的离散单求和不等式和双求和不等式来估计LKF差分中的求和项,并研究了线性离散时滞系统的稳定性问题。文献[20]和文献[21]证明了含有三重求和形式的LKF可有效降低延迟束缚结果的保守性。文献[22]利用含有三重积分形式的LKF,研究了具有混合时变时滞的网络控制系统的稳定性及动态输出反馈控制问题。需注意的是,LKF中含有三重积分或三重求和的形式在1-D系统被广泛应用[23-24],并且取得较好结果,但是在2-D模糊系统几乎没有被应用。因此,本文尝试将含有三重求和的LKF应用到2-D T-S模糊时滞系统,研究其稳定性及状态反馈H∞控制问题。
本文研究了由Fornasini-Marchesini (FM)模型描述的2-D T-S模糊时滞系统的状态反馈H∞控制问题。选取了含有三重求和的LKF,并利用求和不等式对其进行处理,得到了系统的稳定性条件。在此基础上,设计控制器,保证系统的H∞性能。最后,通过数值算例,证明系统稳定,验证了结果的可行性以及准确性。
1 问题描述和准备工作
考虑以下基于模糊规则描述的2-D T-S模糊离散时滞系统:
规则k:如果θ1(i,j)是Θk1,θ2(i,j)是Θk2,…,θp(i,j)是Θkp,那么
x(i+1,j+1)=A1kx(i+1,j)+A1dkx(i+1,j-d1(j))+A2kx(i,j+1)+A2dkx(i-d2(i),j+1)+
B11ku(i+1,j)+B12ku(i,j+1)+B21kω(i+1,j)+B22kω(i,j+1);
(1)
z(i,j)=G1kx(i,j)+L1kω(i,j),
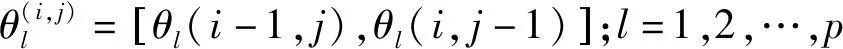
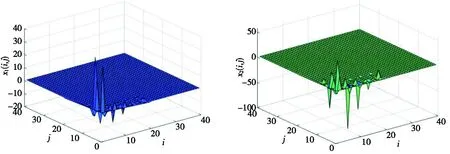
0 (2) 其中:d1m、d2m、d1M、d2M是正整数,表示延迟边界。 使用中心平均去模糊化方法,2-D模糊时滞系统(1)可以表示为: (3) 为了书写方便,系统(3)可以写成以下形式: x(i+1,j+1)=A1μx(i+1,j)+A1dμx(i+1,j-d1(j))+B11μu(i+1,j)+B12μu(i,j+1)+ A2μx(i,j+1)+A2dμx(i-d2(i),j+1)+B21μω(i,j+1)+B22μω(i+1,j); (4) z(i,j)=G1μx(i,j)+L1μω(i,j), 其中: 为了使系统(4)稳定,给出了以下模糊控制定律。 规则k:如果θ1(i,j)是Θk1,θ2(i,j)是Θk2,…,θp(i,j)是Θkp,那么 u(i,j)=Kkx(i,j)。 (5) 通过模糊规则: u(i,j)=Kμx(i,j), (6) 因此,系统(4)可以写成 A2dμx(i-d2(i),j+1)+B21μω(i+1,j)+B22μω(i,j+1); (7) z(i,j)=G1μx(i,j)+L1μω(i,j), 定义1[4]如果满足以下条件,则称具有零边界条件的2-D T-S模糊系统(4)具有H∞扰动衰减度γ: (1)当ω(i,j)=0,系统(4)是渐近稳定的; 其中: Δx1(i,j)=x(i+1,j)-x(i,j);Δx2(i,j)=x(i,j+1)-x(i,j); 其中: Δx1(i,j)=x(i+1,j)-x(i,j);Δx2(i,j)=x(i,j+1)-x(i,j); 本节提出了一种新的2-D T-S模糊时滞系统稳定性分析方法,以LMI的形式给出了在ω(i,j)=0的情况下,系统(4)渐近稳定的充分条件。 定理1 给定标量dkm,dkm,dkM(k=1,2),时滞d1(j),d2(i)满足式(2),如果存在对称正定矩阵P>0,Q>0,Rk>0,Zk>0,Sk>0,Sk+2>0(k=1,2),有如下LMI成立: (8) 其中: y(1,l+1)=x(1,l+1)-x(1,l);y(l+1,1)=x(l+1,1)-x(l,1);d12=d1M-d1m;d21=d2M-d2m; φ1=diag{(d12+1)Q1+R1-Q+6S1,(d21+1)Q2+R2+Q-P+6S2,-Q1,-Q2};φ2=04×4; 则系统(4)在ω(i,j)=0的情况下是渐近稳定的。 证明首先,考虑以下LKF: 然后,通过差分规则ΔV=V1-Vd1-Vd2产生差值,差分结果为: 根据引理1和引理2有: 其中: 定义 其中: 使用Schur补引理,可以得到不等式(8),也就是说,系统(4)是渐近稳定的。 定理1已经给出了系统(4)在ω(i,j)=0时的稳定性结果,除此之外,实际应用时还需要考虑系统的性能,所以定理2和定理3将研究系统(7)在ω(i,j)≠0时的H∞性能以及控制器设计问题。 定理2 给定标量γ和dkm,dkM(k=1,2),时滞d1(j),d2(i)满足式(2),如果存在对称正定矩阵P>0,Q>0,Rk>0,Zk>0,Sk>0,Sk+2>0(k=1,2)有如下LMI成立: (9) 其中: 则系统(7)具有给定的H∞扰动衰减水平γ。 证明由于式(8)可以从式(9)推导出来,通过定理1,可以从式(9)中得到系统(7)在ω(i,j)=0的情况下是渐近稳定的。 (10) 为验证上述定理的有效性及正确性,将其应用于化学反应器、热交换器或管式炉中的热过程,可以用以下具有时间延迟的部分可微方程来表示: 其中:T(x,t)在空间x中表示温度;t表示时间;τt表示时间延迟;a(.)=a(x,t,T(x,t)),b=(.)=b(x,t,T(x,t))是取决于T(x,t)的状态的系数函数。 假设 可得到以下2-D非线性模型: 定义xT(i,j)=[TT(i-1,j)TT(i,j)],从而很容易地获得以下2-D FM模型: x(i+1,j+1)=A1x(i,j+1)+A2x(i+1,j)+A1dx(i-d1(i),j+1)+A2dx(i+1,j-d2(j)), 其中: 令Δt=1,Δx=1,a(.)=-0.7+0.3sin2(T(i,j)),b(.)=0.5-cos2(T(i,j))。 考虑以下两个sin2(T(i,j))规则,进而获得2-D T-S模糊系统。 规则1:如果sin2(T(i,j))是0,那么 x(i+1,j+1)=A111x(i,j+1)+A121x(i+1,j)+A1d1x(i-d1(i),j+1)+A1d2x(i+1,j-d2(j))。 规则2:如果sin2(T(i,j))是1,那么 x(i+1,j+1)=A212x(i,j+1)+A222x(i+1,j)+A2d1x(i-d1(i),j+1)+A2d2x(i+1,j-d2(j)), 其中: 隶属函数由下式给出: 此外,为了考虑扰动问题,该过程建模为式(3)的形式: 并且给定参数t1=0.02,t2=0.05,t3=0.24,t4=0.2,t5=0.02,t6=0.3,则有: 仿真结果如图1和图2所示。由图1和图2可知:在初始阶段,状态曲线有明显的波动。随着i和j的增加,状态响应逐渐趋向于0。这意味着系统(7)具有预先给定的H∞扰动衰减水平γ=1。 图1 系统(7)状态变量x1(i,j)轨迹 图2 系统(7)状态变量x2(i,j)轨迹 在实际系统中,时滞是存在的,还会随着环境变化,可能会带来不理想的性能甚至引起系统不稳定,所以研究时变时滞系统具有重要意义。本文提出了一种含有更多时滞信息的三重求和的LKF,并针对基于FM模型描述的2-D T-S模糊时滞系统,研究了其稳定性及H∞控制问题。将理论分析应用到热过程中,通过数值算例,验证了所得定理的准确性。此外,本文选取新的 LKF,包含更多的时滞信息,所以得到的结果也更适用于含有时变时滞的2-D T-S模糊系统,虽然本文研究了2-D T-S模糊时滞系统,但是由于信号通过不同轴突大小和长度的平行路径传输的空间特性,分布时滞也在影响着系统稳定。因此,未来将在此方法上进行改进,研究带有离散时滞和分布时滞的2-D T-S模糊系统的稳定性及控制问题。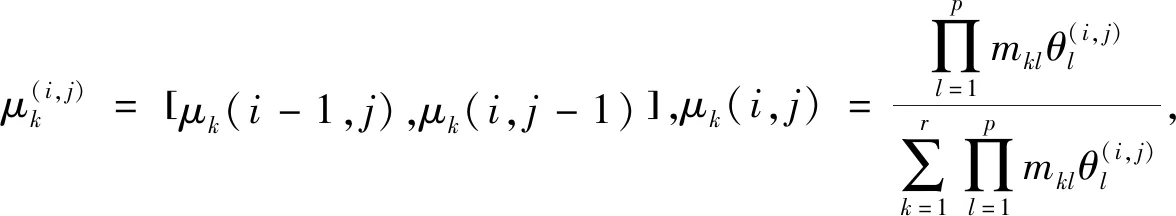
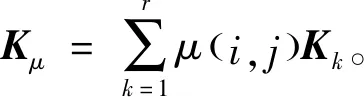
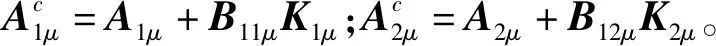
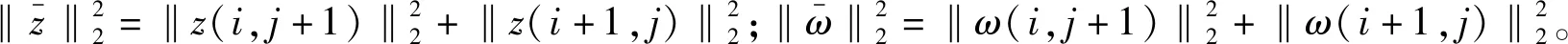
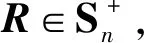
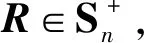
2 稳定性分析与控制器设计
2.1 稳定性分析
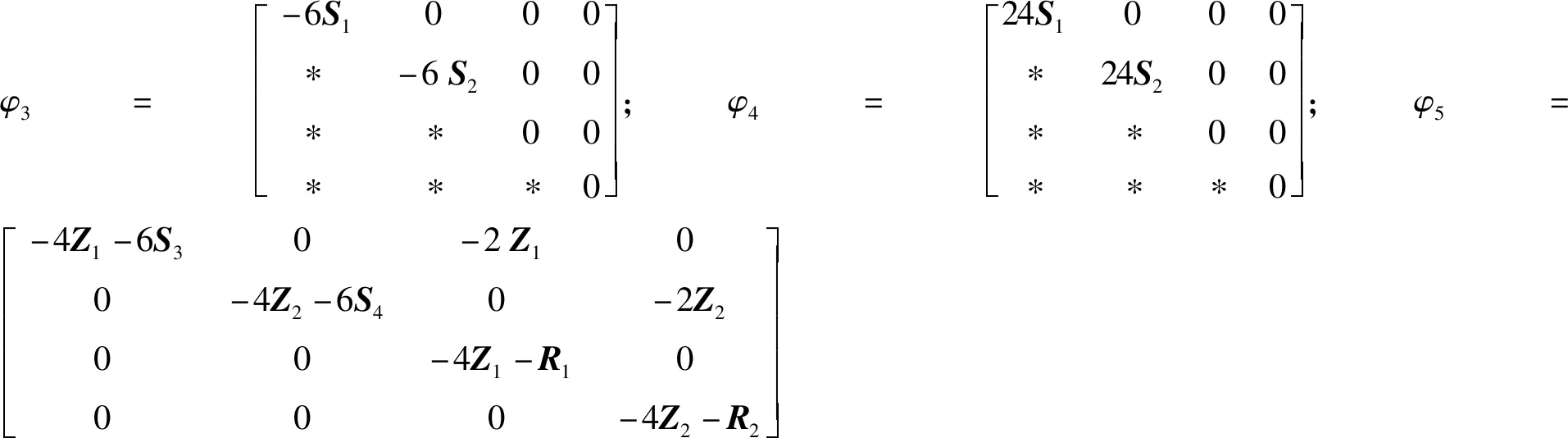
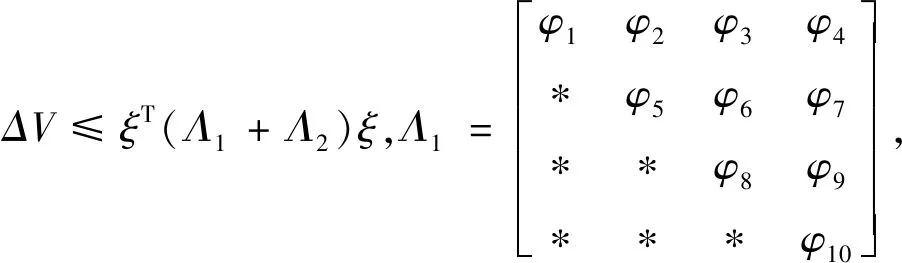
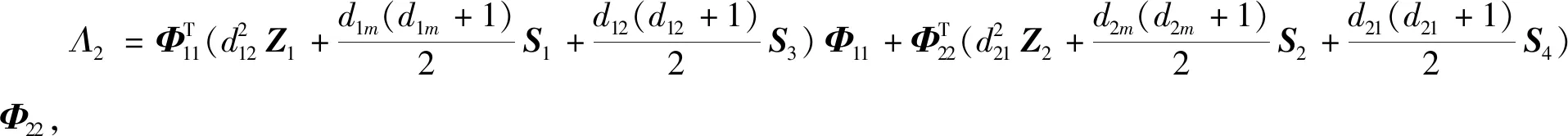
2.2 H∞性能分析与控制器设计
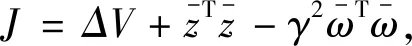
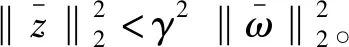
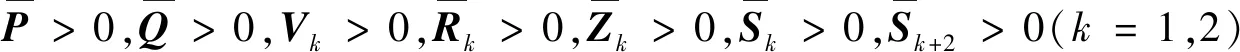
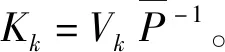
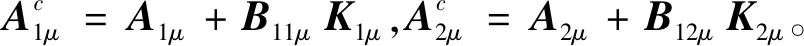
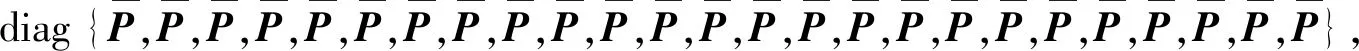
3 数值算例
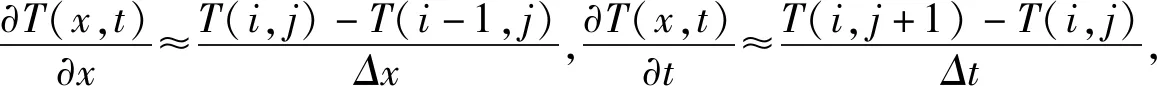
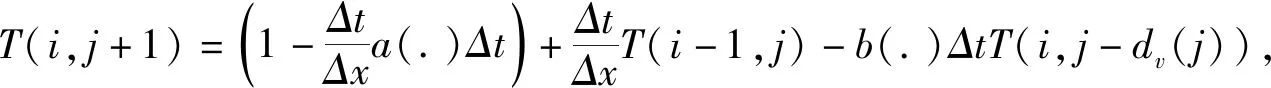
4 结论

