非化学计量比对(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的显微结构和微波介电性能的影响

李 谦，高 顺，顾永军，张豪杰，李丽华，黄金亮

(河南科技大学 材料科学与工程学院，河南 洛阳 471023)

0 引言

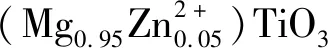
综上所述，本研究以Zn2+掺杂结合非化学计量比，可降低陶瓷烧结温度、抑制有害的第二相，提高了材料的Qf。

1 试验材料与方法

采用固相法合成陶瓷粉体，试验原料：MgO(质量分数>98.5%)、TiO2(质量分数>99%)和ZnO(质量分数>98%)。

以(Mg0.95Zn0.05)1+δTiO3+δ(δ=-0.1，0，0.1，0.2和0.3)配比，随后球磨20 h，烘干后在1 100 ℃下预烧4 h。所得粉体经过二次球磨后，加入质量分数约5%的聚乙烯醇进行造粒，然后在100 MPa的压力下干压成圆片(直经10 mm，高度5 mm)。最后，把试样放入烧结炉中以5 ℃/min的升温速度升至1 340～1 390 ℃，保温4 h，随炉冷却。作为对比，纯MgTiO3陶瓷采用相同工艺制备，烧结温度分别为1 365 ℃、1 390 ℃和1 415 ℃。在1 390 ℃烧结后，密度最高，相对密度达到95.6%，微波介电性能：相对介电常数εr=17，品质因数Qf=108 000 GHz，谐振频率温度系数τf=-42×10-6℃-1。

采用X射线衍射仪(D8 Bruker Advance型)检测陶瓷的物相组成，测试条件： Cu-Kα射线，衍射角20°～60°，扫描步长为0.02°。采用阿基米德排水法测量陶瓷烧结样品的体积密度。通过扫描电子显微镜(JEOL JSM5610LV)对溅射Au薄膜后的陶瓷表面进行观察和分析。陶瓷的微波介电性能通过矢量网络分析仪(Agilent N5230C)采用闭腔法进行测试。τf由式(1)计算：

(1)

其中：f1为70 ℃下谐振频率，GHz；f2为20 ℃下谐振频率，GHz；t1为70 ℃；t2为20 ℃。

2 试验结果与分析

图1为1 365 ℃烧结4 h后的(Mg0.95Zn0.05)1+δTiO3+δ陶瓷和MgTiO3陶瓷的X射线衍射图谱。由图1可知：纯MgTiO3陶瓷烧结后除了MgTiO3主晶相外，还产生了第二相MgTi2O5，这种情况在不同烧结温度下同样存在，验证了其易形成第二相的问题。不同δ的 (Mg0.95Zn0.05)1+δTiO3+δ陶瓷均以(Mg0.95Zn0.05)TiO3(标记为MgTiO3相， PDF#79-0831)为主晶相。当δ=-0.1时，还有少量第二相(Mg0.95Zn0.05)Ti2O5(标记为MgTi2O5相， PDF#79-0833)生成，这是由Mg的缺失所致。当δ为0～0.2时，物相全部为MgTiO3单一相。而根据文献[15]的研究，非化学计量比的Mg1+δTiO3+δ陶瓷在0≤δ≤0.02时，才能保持单一MgTiO3相。由于Zn2+半径(0.074 nm)与Mg2+半径(0.072 nm)[16]相近，导致Mg2+容易被Zn2+取代形成钛铁矿结构的 (Mg0.95Zn0.05)TiO3固溶体。非化学计量比条件下Zn2+的掺杂，使固溶体的固溶度增加了10倍，很大程度上扩大了MgTiO3相存在的范围，从而有效避免了第二相的生成。δ继续增大至0.3时，会有少量第二相(Mg0.95Zn0.05)2TiO4(标记为Mg2TiO4相， PDF#87-1174)生成，说明这时已超过固溶体的极限固溶度。

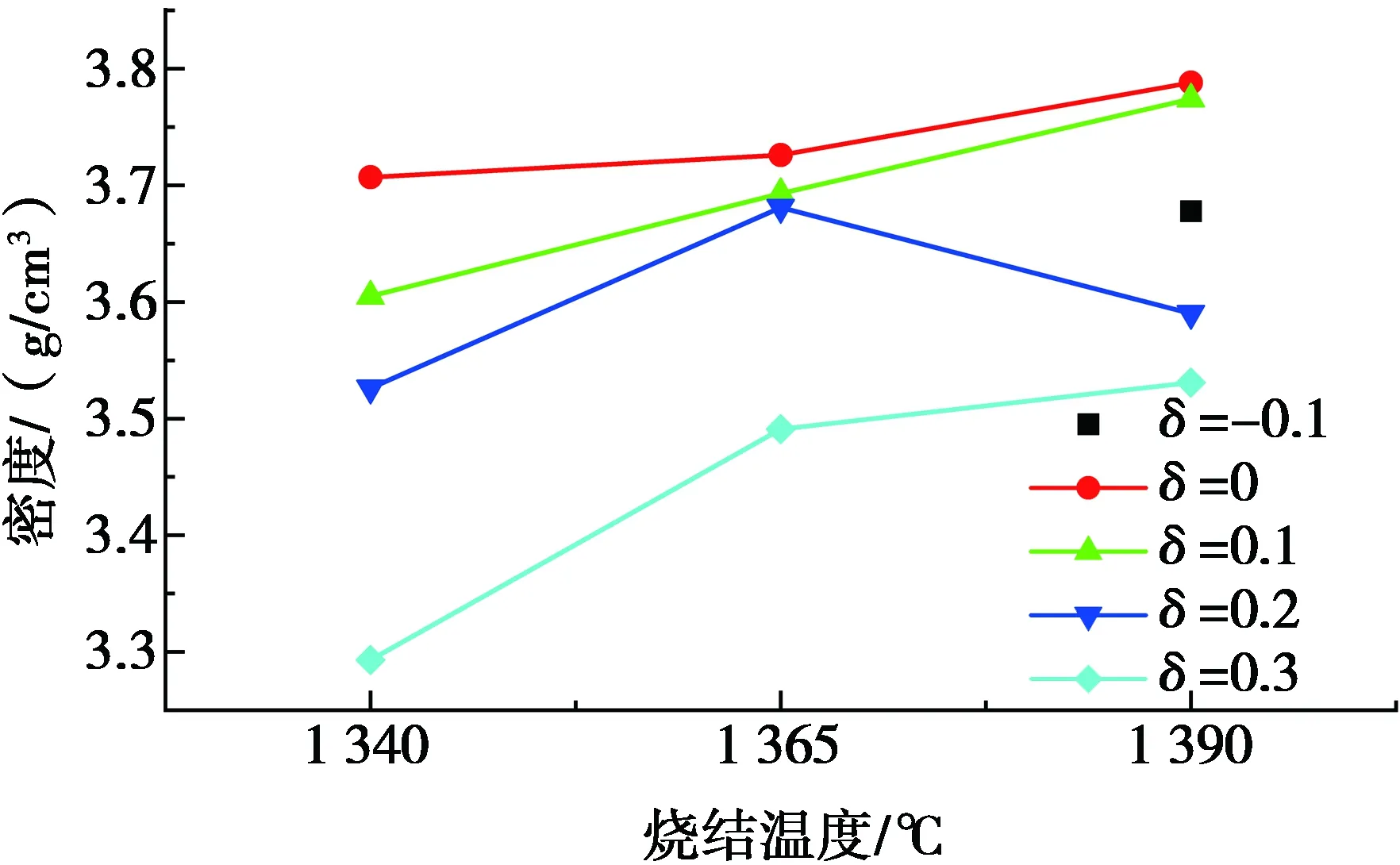
图2 在不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的体积密度

图2是在不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的体积密度。当δ=-0.1时，密度较低，这是由于存在的MgTi2O5第二相的理论密度(3.649 g/cm3)低于MgTiO3相(3.895 g/cm3)。当δ为0～0.1时，获得较大的密度，这是由于单一的MgTiO3相的密度较大。当δ=0.2时，烧结温度为1 365 ℃，(Mg0.95Zn0.05)1.2TiO3.2陶瓷密度达到最大(3.681 g/cm3)，这说明Zn掺杂有利于降低烧结温度。烧结温度达到1 390 ℃后，由于晶粒异常长大，同时，Zn元素在高温下部分挥发，使密度有些降低。当δ=0.3时，其密度较低，是由于出现了烧结温度更高的第二相Mg2TiO4，烧结不充分，导致气孔较多。

图3为不同烧结温度的(Mg0.95Zn0.05)1+δTiO3+δ陶瓷显微结构的扫描电镜照片。由图3可以看出：δ=0时(见图3a)，晶粒较大，且晶粒大小分布不均，气孔较少。δ=0.1时(见图3b)，晶粒的粒径开始下降,且气孔增加。当δ值继续增加到0.2时(见图3c)，晶粒尺寸依旧下降，同时晶粒大小分布较为均匀，气孔较少，并随着烧结温度达到1 365 ℃时，陶瓷晶粒分布均匀，气孔最少，最为致密(见图3d)。而其烧结温度为1 340 ℃时(见图3e)，可以看到晶粒较小，且分布不均，并没有达到最佳烧结温度。当δ=0.3时(见图3f)，可以看到有一定数量的Mg2TiO4相小晶粒，这与图2中当δ=0.3时存在第二相Mg2TiO4相的现象一致。

(a) δ=0，烧结温度1 390 ℃ (b) δ=0.1，烧结温度1 390 ℃ (c) δ=0.2，烧结温度1 390 ℃

图4为不同δ值在不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的相对介电常数。陶瓷的介电常数与其相组成、气孔等有关[17]。本研究中不同烧结温度的(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的εr整体随着δ值增加逐渐降低，在1 365 ℃时最为明显，此时，在δ=0.2时，εr=16.5。

图5为不同δ值在不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的品质因数。由图5可知：纯MgTiO3陶瓷1 390 ℃烧结后，由于存在Qf很低的第二相MgTi2O5，Qf仅为108 000 GHz。不同烧结温度的(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的δ值一定时，随着烧结温度的上升，Qf的变化与密度变化基本相同，说明Qf主要受气孔的影响。当δ=-0.1，同样由于存在第二相MgTi2O5，导致材料的Qf较低(88 000 GHz)。随着δ增加，Qf整体上逐渐增大，在δ=0.2，经1 365 ℃烧结后，可以获得最高的Qf，达到166 000 GHz。这主要归因于单一的(Mg0.95Zn0.05)1.2TiO3.2固溶体和均匀致密的晶粒。在δ=0.3时，Qf有所下降，这可能是存在少量Mg2TiO4第二相，但由于其Qf仅略低于MgTiO3相的Qf，所以，最终材料的Qf依然可以达到144 000 GHz。

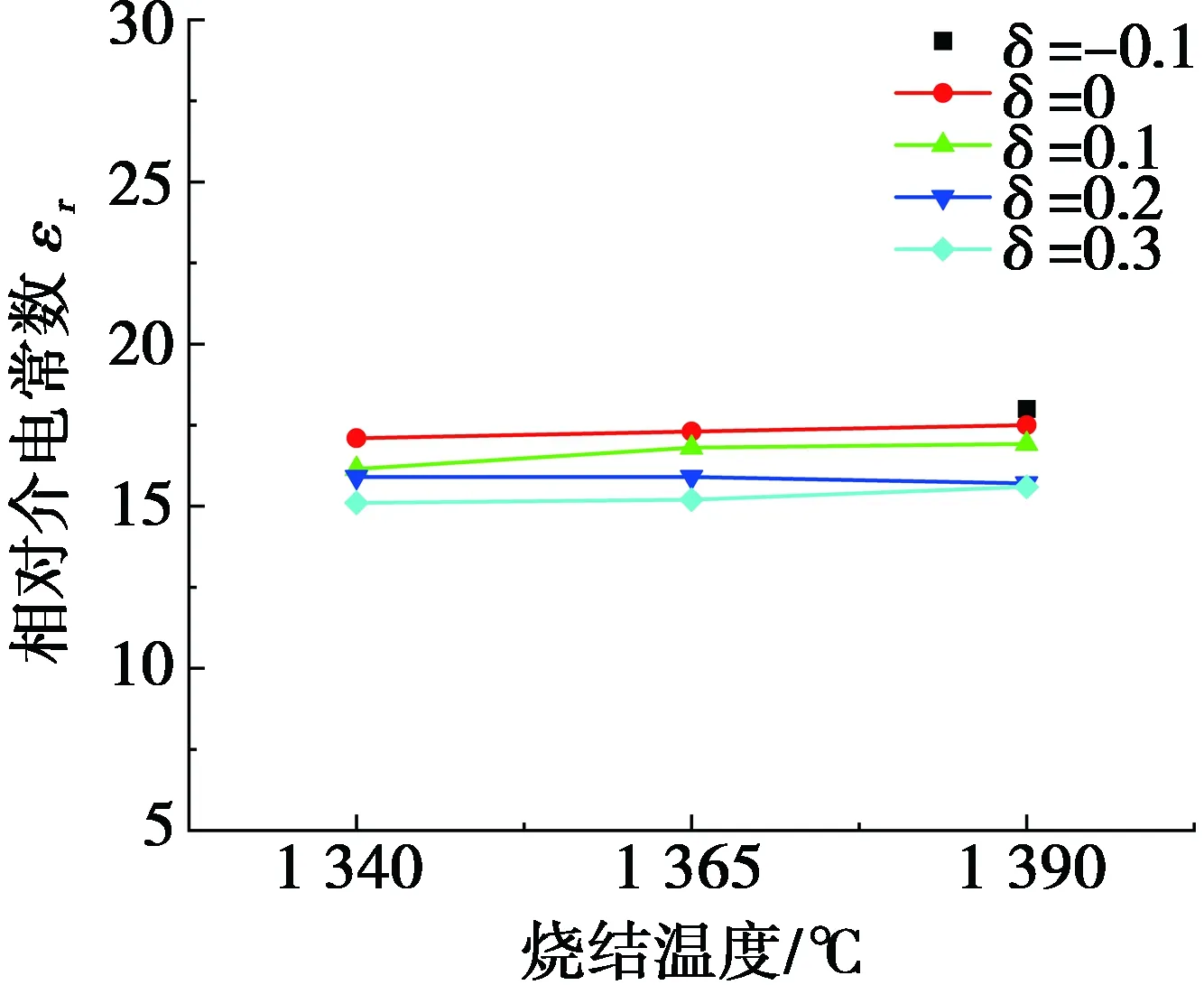
图4 不同烧结温度下 (Mg0.95Zn0.05)1+δTiO3+δ陶瓷的相对介电常数

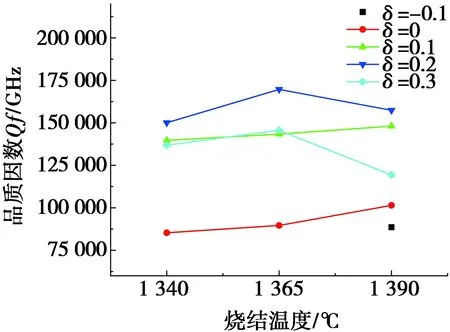
图5 不同烧结温度下 (Mg0.95Zn0.05)1+δTiO3+δ陶瓷的品质因数Qf

文献[14]把Mg1.02TiO3.02陶瓷高的Qf归因于单一MgTiO3相、高的密度和均匀粗大的晶粒。也有一些研究表明晶粒的大小对品质因数的影响比较复杂[18-19]。本研究中，随着δ值的增加，晶粒尺寸减小，说明晶粒的大小对高的品质因数贡献不大。MgTiO3陶瓷为六方钛铁矿型结构，[TiO6]八面体层被两层[MO6]八面体层包夹，每个氧八面体沿c轴共面，在ab面内共边，而沿倾斜方向共顶点。一对共边的[TiO6]八面体在ab面内被阳离子空位所隔离，而在倾斜方向被[MO6]八面体隔离[20]。MgTiO3陶瓷中[TiO6]八面体之间共面和共边的结构特征使其具有低的介电常数和高的Q值。[TiO6]八面体的连接方式与其介电常数和Q值有关。[TiO6]八面体的隔离导致介电常数的降低和Q值的增加，这归因于[TiO6]八面体之间的协同作用减弱[20]。当δ值增加时，[MO6]八面体的数量增加，[TiO6]八面体会被更多的[MO6]八面体隔离，进一步减弱了[TiO6]八面体间的协同作用，导致介电常数的降低和Q的增加。本研究中，Q增加的幅度比介电常数的降低幅度更大，说明[MO6]八面体隔离对高的Q影响更为显著。

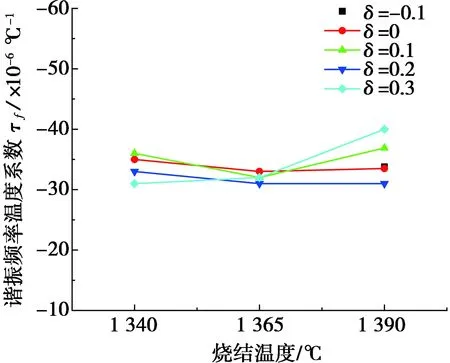
图6 不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的谐振频率温度系数τf

图6为不同烧结温度下(Mg0.95Zn0.05)1+δTiO3+δ陶瓷的谐振频率温度系数τf。由图6可以看到：τf为-31×10-6～-42×10-6℃-1，说明以非化学计量比与Zn元素掺杂对陶瓷τf的影响较小。

最后，当δ=0.2，(Mg0.95Zn0.05)1.2TiO3.2陶瓷1 365 ℃烧结时，晶粒最为致密，获得了最佳微波介电性能，εr=16.5，Qf=166 000 GHz，τf=-37.2×10-6℃-1。陶瓷样品在δ为0～0.2保持单一相，具有较好的介电性能，这对实际的生产有着重要意义，在配料方面有着更大的容错率。同时也为MgTiO3陶瓷提供了多元掺杂的可能性。

3 结论

(1)(Mg0.95Zn0.05)1+δTiO3+δ陶瓷可在0≤δ≤0.2保持MgTiO3单相，Zn离子掺杂在很大程度上扩大了MgTiO3单相存在的范围。

(2)随着δ增加，Qf整体上逐渐增大，当δ=0.2时，1 365 ℃烧结时Qf最高，可达166 000 GHz，此时，εr=16.5，τf=-37.2×10-6℃-1。高Qf与致密的MgTiO3单相和结构中[MO6]八面体隔离作用有关。

(3)当δ为-0.1和0.3时，则分别出现了MgTi2O5和Mg2TiO4第二相，导致Qf在不同程度上有所降低。