农村金融规模、农村金融效率与农村经济增长

刘炯

(宣城职业技术学院 旅游商贸系，安徽 宣城 242000)

自Patrick开创发展中国家经济增长与金融发展关系研究之先河[1]，对农村金融与农村经济关系的探求风靡云蒸。农村金融的发展助推了农村经济增长，改善了农民生活水平[2]，但农村经济增长未能繁荣农村金融[3]，如果农村金融市场得不到改善，其发展势必会抑制农村经济增长[4]，尤其是在发展中国家，农村低廉的信贷成本不但无法促进农村经济发展，相反却侵蚀了农村经济发展的根基[5]67。

基于全国层面或省域范围数据，国内学者往往将农村金融划分为规模、效率两个维度或规模、效率与结构三个维度，选取不同的模型方法对农村金融与农村经济的关系做出了许多有益的研讨。有人采用帕加诺模型，认为农村金融规模与效率皆非推动湖北省农村经济增长的显著性因素[6]，罗振军的实证检验指出，农村金融规模与效率显著地推动了浙江省农村经济的增长[7]。而有人采用VAR(Vector Auto-regression)模型，发现农村金融规模与效率在长期内均对我国农村经济具有明显的负向影响[8]，高维新等、孔凡斌等证实了农村金融规模的增大与效率的提高能增加农民收入[9，10]。有研究表明农村金融效率显著地正向作用于农村经济增长且具有正向空间溢出效应，农村金融规模与结构显著地负向冲击农村经济增长[11]，还有研究显示农村金融在东中西部三个地区对农村经济的作用具有明显的区域性特征[12]。

综观现有文献，由于研究方法的差别、研究对象的相异以及研究数据的不同，农村金融发展与农村经济增长的关系纷繁复杂，国内外学者并未形成统一的观点，存在着较大的争议与分歧甚至相左。近年来，传统农业大省安徽省农村金融市场不断发展，而农村金融基础设施不够完善、农村金融产品难以满足农村经济发展需求等一些现象仍然存在。那么，安徽省农村金融发展是否影响安徽省农村经济增长？如果影响，其影响方向与影响程度如何？这些都是值得深入探讨的重要问题。

1 模型设定、指标选取与数据说明

1.1 模型设定

借鉴Feder、Odedokun与Pagano的研究，将农村金融发展视作一项独立的投入要素引入总量生产函数，反映农村经济总产出和农村金融发展的生产函数如下：

Y=f(K,L,F)

(1)

式中：Y、K、L与F顺次代表农村经济总产出、资本投入、劳动力投入和农村金融。对(1)式全微分，得到：

(2)

以农村金融发展现状为基础，参考已有的研究，从农村金融规模(FS，Financial scale)与农村金融效率(FE，Financial efficiency)两个维度考察农村金融，对其全微分并代入式(2)，得到本文基本计量模型：

dY=α0+α1dFS+α2dFE+α3dK+α4dL+μ

(3)

式中：α1、α2、α3、α4依次表示农村金融规模的边际产出、农村金融效率的边际产出、农村资本投入的边际产出、农村劳动力投入的边际产出，α0代表常数项，μ是随机误差项。

关于VAR模型的研究，已从早期的二维发展到当前的多维。现实中，FS、FE、K与L对Y的影响具有一定的滞后性，为了实证分析安徽省农村金融发展对农村经济增长的影响，构建向量自回归模型如下：

(4)

式中：i为滞后阶数，t为时间期数。

1.2 指标选取

1)农村经济增长指标。经济增长通常被规定为产量的增加，而产量既可用总产量来表示，也可用人均产量来表示，经济增长的程度则采用增长率来度量。由于现有的官方统计资料查不到农村GDP数据，参照王琼等[6]、罗振军[7]、高维新等[9]等学者的做法，使用人均第一产业生产总值(元)，该指标为人均产量，业已去除人口数量变动对计量结果的影响，为了反映实际经济水平，以1990为基期，定值为100，采用CPI对其进行调整。为了压缩数据的波动幅度进而尽可能地使数据平稳以避免产生异方差，对变量指标取对数，简记为LGRGDP。对数据加以对数变换，不会改变原来存在的协整关系。

2)农村金融发展指标。尽管安徽省农村金融市场金融机构众多，但合作金融仍是主力军，长期在农村金融市场唱着“独角戏”，故用农村合作金融代表农村金融。借鉴罗振军[7]、孔凡斌等[10]、王淑英等[11]等人的做法：采用农村合作金融存贷款总额与第一产业生产总值之比表示农村金融规模，该指标越大，表明农村经济活动的货币化程度越高，取对数后记为LGFS；采用农村合作金融贷款总额对存款总额比例表示农村金融效率，该比值越大，说明农村金融中介将存款转化为贷款的比重越大，对数化后记为LGFE。

3)农村资本投入与劳动力投入指标。本文考察安徽省农村金融对农村经济的影响，在总量生产函数的基础上建立计量模型，将资本投入与劳动力投入视为控制变量。参考温红梅等[12]的做法，采用农业机械总动力(万千瓦)作为农村资本投入的代理变量，它是全部农业机械设备额定动力总和，对数化后记为LGRK；参考廖宏伟等[13]的做法，采用第一产业就业比例表示农村劳动力投入，由第一产业就业人数除以三次产业就业总人数得到，取对数后记为LGRE。

1.3 数据说明

本研究选取安徽省1992—2019年合计28年的年度时间序列数据，探究农村金融发展对农村经济增长的影响。全部数据包括安徽省第一产业生产总值、农业人口数、农村合作金融存贷款总额、农业机械总动力、第一产业就业比例以及各年度的消费者物价指数，皆来源于1993—2020年的《安徽统计年鉴》。

2 安徽省农村金融发展对农村经济增长影响的实证分析

2.1 平稳性检验

时间序列平稳是经典计量经济分析的前提，也是VAR模型的基础。为防止伪回归，首先对数据执行平稳性检验。如果经检验序列不平稳，则需要差分处理并对差分变量继续检验，继而判别是否存在协整关系。由EVIEWS软件依据AIC(赤池信息准则)与SC(施瓦次准则)自行明确最优滞后期，选用当前使用的最为普遍最为频繁的ADF(Augmented Dickey-Fuller)单位根检验法，检验结果反映，序列LGRGDP、LGFS、LGFE、LGRK、LGRE的ADF检验值皆大于各自的5%临界值且概率值都大于0.05，接受原假设存在单位根，得以判定5%显著水平下五个变量都是非平稳的。对它们逐个取一阶差分，在5%的显著性水平下，五个一阶差分变量的ADF检验值均小于临界值且概率值都小于0.05，所以都是平稳序列。综合判断，原序列LGRGDP、LGFS、LGFE、LGRK、LGRE在5%显著水平皆为一阶单整，即I(1)过程，符合协整检验的条件，是以需要检验变量LGRGDP、LGFS、LGFE、LGRK、LGRE之间是否存在协整关系。2.2协整检验

E-G两步法与Johansen协整检验为目前最常用的两种协整检验方法，前者以回归方程残差为基础，后者则针对多变量实施协整分析。于是，运用Johansen协整检验法对五个变量LGRGDP、LGFS、LGFE、LGRK、LGRE展开协整分析，表1为检验结果。表1选择最大特征值标准予以评价Johansen协整检验，假设只有两个协整方程最大特征值18.5130大于临界值17.7973，拒绝原假设，至少存在两个协整方程；假设只有三个协整方程的最大特征值10.6526小于临界值11.2248，接受原假设，最多有三个协整方程。所以，变量LGRGDP、LGFS、LGFE、LGRK、LGRE之间具有协整关系，即存在长期稳定的均衡关系。

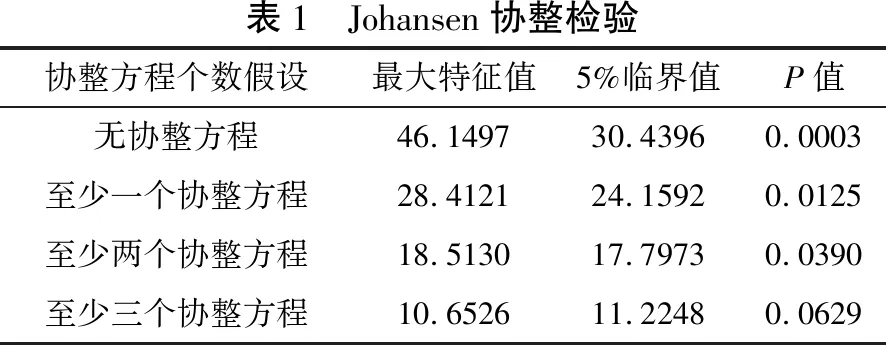
表1 Johansen协整检验协整方程个数假设最大特征值5%临界值P值无协整方程46.149730.43960.0003至少一个协整方程28.412124.15920.0125至少两个协整方程18.513017.79730.0390至少三个协整方程10.652611.22480.0629

由表2输出的标准化协整系数可得标准化的协整方程为

LGRGDP=-0.0075LGFS-1.2597LGFE+0.6930LGRK-0.8062LGRE

(5)

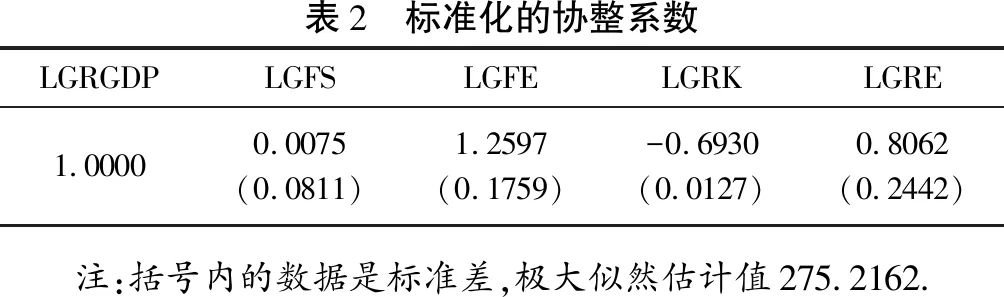
表2 标准化的协整系数LGRGDPLGFSLGFELGRKLGRE1.00000.0075(0.0811)1.2597(0.1759)-0.6930(0.0127)0.8062(0.2442) 注:括号内的数据是标准差,极大似然估计值275.2162.

根据方程(5)，在样本区间内，LGRGDP、LGFS、LGFE、LGRK、LGRE具有长期均衡关系，LGRGDP与LGRK正相关，LGRGDP与LGFS、LGFE、LGRE负相关，即安徽省农村经济增长LGRGDP与农村资本投入LGRK正相关，与农村金融规模LGFS、农村金融效率LGFE以及农村劳动力投入LGRE负相关。

协整分析说明，农村金融规模扩大，微弱的负向影响农村经济增长，农村金融规模每增加1个单位，农村经济微弱的减少0.0075个单位。样本区间内的安徽省农村合作金融存贷差逐年加大，2019年高达3040.1亿元，27年间累计净外流资金超过24200亿元，农村合作金融机构从农村金融市场吸纳的资金，未能真正发挥其应有的支农作用。更深层次的原因是，政府巧妙地利用其垄断的金融体系把大量的农村资金转移至城市，优先支持城市建设与工业发展。从1990年代中后期，国有商业银行大量从县域地区撤出，包括农业银行在内的仅存的网点对农村地区业务重点是吸收存款。农村合作金融是农村金融市场的主力军，但由于其公司治理不够完善，再加上累积的历史包袱，独木难支，难以供给农村地区日益扩大的金融需求。因而，随着农村金融规模的逐步扩张，农村资金从农村地区持续地净流出，反而微弱地阻碍了农村经济的增长。

协整分析表明，农村金融效率提高，不利于农村经济增长，农村金融效率每增加1个单位，农村经济下降1.2597个单位。安徽省农村经济长时期的发展滞后引起城乡收入差距不断扩大，城乡人均可支配收入差距由1992年的1222元增长到2010年的10502元，2019年则为22124元。长期的计划生育政策，农村独生子女明显增多，教育与医疗保健费用不断加大；农村向城市看齐，增加了家庭支出；城镇化迅速发展时期，很多农村家庭欲落户城镇，在高房价时代，更加不堪重负。因此，农户获得贷款后，将资金过多地用于子女教育、医疗、购房、婚丧嫁娶与日常生活，并没有投资生产领域，最终负向影响农村经济增长。

协整分析还说明，农村资本投入正向影响农村经济增长，即增加农田水利基础设施建设以及农村固定资产与农业机械设备投资，改善生产条件，以便助力农村经济增长；农村劳动力投入负向影响农村经济增长，即在其他要素投入一定以及技术不变的前提下，将农村过剩的劳动力转移出去，劳动投入的边际产量上升，提高了劳动效率，有利于农村经济增长。

2.3 格兰杰因果关系检验

为了深入地探讨安徽省农村金融发展对农村经济增长的影响，协整分析后需要进行格兰杰因果关系检验，以便确认LGRGDP与LGFS、LGFE、LGRK、LGRE之间是否以及存在怎样的因果关系。

检验结果显示，在5%的显著性水平下，LGRGDP与LGFS存在双向格兰杰因果关系，LGFE仅是LGRGDP在10%显著性水平下的单方向格兰杰原因。考量协整分析揭示的农村金融规模、效率负向影响农村经济增长，格兰杰因果关系检验进一步解释了农村金融规模的扩大、农村金融效率的提高皆抑制了农村经济增长。从资金的投资收益率来看，城市高于农村，工业高于农业，农村金融规模的扩大，反而导致更多的资金从农村流向城市，从农业流向工业，抑制了农村经济的增长。该检验的言外之意是，如果农村经济发展水平提高，其投资收益率就能较快增长，就会吸引更多的资金投资于农村。

检验结果还显示，LGRK与LGRGDP在5%显著性水平下不存在格兰杰因果关系，原因是农村经济主要表现为自力更生式的发展，财政资源较少地投入农村与农业，农村资本投入在较大程度上依靠农村经济自身增长带动；LGRGDP不是LGRK的格兰杰原因，LGRK是LGRGDP的格兰杰原因，说明农村经济增长吸纳不了过多的农村劳动力，劳动生产效率的提高转移过剩的劳动力将有利于农村经济的增长。

2.4 VAR模型的建立

VAR模型滞后期越大，体现的动态关系信息就越多，同时模型的自由度就越小，所以应对滞后期与自由度寻求一种最佳的均衡状态。一般情况下，依据AIC与SC选定最优滞后期，如果两个准则在某一期同时达到最小，则该期为最优滞后期；如果两个准则不能同时达到最小，则需要通过LR(似然比)统计量来判断。本研究，AIC与SC不能同时取得最小，滞后1期，LR统计量与SC准则取得最优，因而最优滞后期为1期，可以建立无约束VAR(1)模型。

脉冲响应函数分析与方差分解，均以稳定的VAR模型为基础，所以必须对VAR模型进行稳定性检验。本文的VAR(1)模型有5个特征根，对应的倒数的模分别为0.97、0.77与0.25，皆小于1，都在单位圆之内，因而该VAR(1)模型符合稳定性条件。

2.5 脉冲响应函数分析

为了比较全面地分析LGFS、LGFE、LGRK与LGRE对LGRGDP的短期动态影响，需要实行脉冲响应函数分析与方差分解，绘制脉冲响应函数如图1～5所示，实线表示1单位标准差冲击的脉冲响应函数时间路径，虚线则表示两个标准差的置信区间。

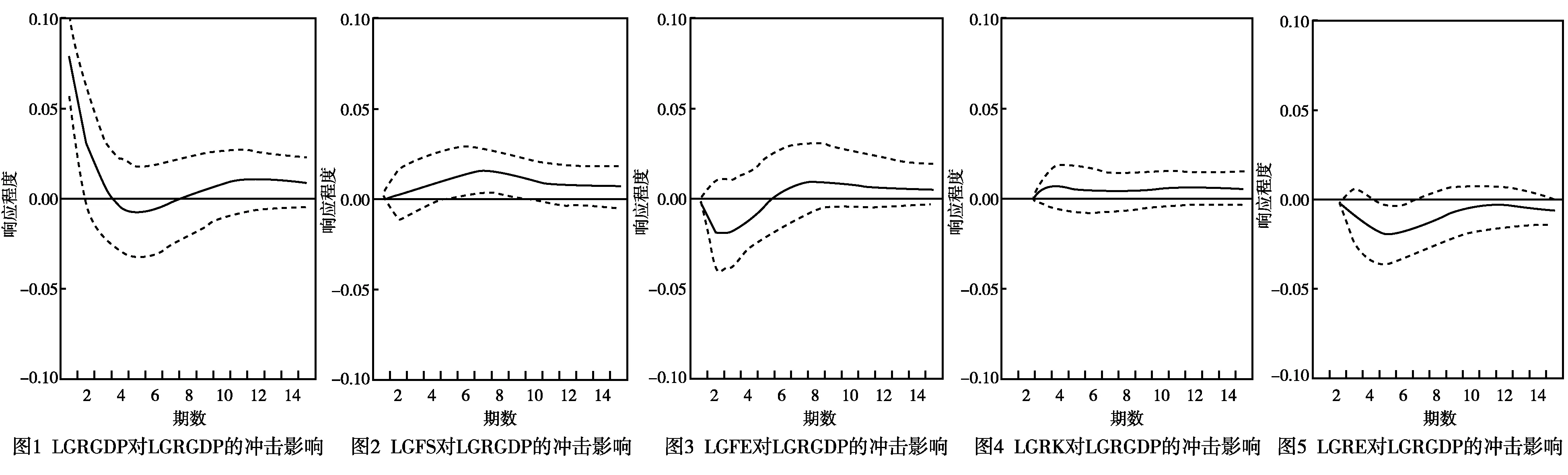
图1为LGRGDP对其自身冲击的响应时间路径，LGRGDP对来自自身的一个单位的正向冲击立即做出了最大的响应0.076，随后陡然下降，第4期至第7期全部负效应，第5期降至谷底后缓慢上升，于11期收敛于0.009，说明LGRGDP具有自我强化机制。图2考察来自LGFS冲击之后LGRGDP的变化情况，LGFS的变化对LGRGDP的冲击效应始终为正，先缓慢上升到6期的0.016后缓慢的下降，至15期依旧保持下降趋势。图3表示LGFE对LGRGDP的冲击，即LGFE一个标准差的变动对LGRGDP的脉冲函数图，LGRGDP受到一个单位冲击后即刻表现负向效应并于2期下降到谷底，3期开始上升，8期到达峰顶后缓慢下降，13期收敛于0.007。综合来看，短期内，滞后一期的LGFS、LGFE对LGRGDP带来一个单位正向冲击，对LGRGDP产生的效应渐渐趋向收敛，说明农村金融对农村经济的发展表现稳定的影响。

若给LGRK一个单位的正向冲击，图4中对LGRGDP的脉冲影响第一期为微小的正效应，第2期开始基本稳定在0.007左右。图5的LGRE对LGRGDP一个单位的正向冲击的影响始终为负，第1期开始后表现下降趋势，4期谷底后缓慢上升，9期收敛于-0.006。

2.6 方差分解

为了解释每一个扰动项因素对LGRGDP的相对影响程度，亦即分清来自LGRGDP自身或其他变量冲击而引起的方差变动的比例，需要进行方差分解，如表3所示。

表3 农村经济增长方差分解

由表3可知，第1期的LGRGDP的变化100%由其自身解释；自第2期开始，随着期数的增加，LGFS、LGFE、LGRK与LGRE对LGRGDP方差变动的贡献程度整体上呈现上升趋势，农村经济增长变动方差由其自身变动的贡献度逐步下降。第15期，LGFS、LGFE、LGRK、LGRE对方差变动的贡献度分别为11.3%、12.3%、4.1%、19.3%左右。整体上看，LGFE比LGFS对LGRGDP方差变动的贡献程度要稍大一些，LGRGDP方差变动主要由其自身与LGRE变动来解释。

3 结论与建议

3.1 结论

长期来看，安徽省农村金融规模LGFS与农村金融效率LGFE都和农村经济增长LGRGDP存在协整关系，LGFS、LGFE皆负向影响LGRGDP，农村金融发展与农村经济增长存在长期的均衡关系，这与杜兴瑞等的研究结果保持一致。格兰杰因果关系检验表明，LGFS与LGRGDP存在双向格兰杰因果关系，LGFE是LGRGDP单方向格兰杰原因，样本区间内的LGFE与LGRGDP没有形成良好的互动关系。

短期来看，安徽省农村金融规模LGFS与农村金融效率LGFE对安徽省农村经济增长LGRGDP带来一个单位正向冲击，对LGRGDP产生的脉冲影响渐趋收敛，意即农村金融发展对农村经济增长的影响趋向稳定。方差分解证实，从15期开始，LGFS与LGFE对LGRGDP预测误差的最大影响分别为11.3%与12.3%，表明二者对农村经济增长变化尚有一定的贡献程度与解释能力。

3.2 建议

1)缓解农村资金外流，加大农村金融对农村经济的资金支持。为减缓以至扭转农村资金净流出，首先，政府同样可以利用庞大的正规金融体系，对大型金融机构实行差异化准备金政策，因地制宜地采取税收减免以及贴息补助等措施，甚至硬性规定其对农村经济投入的最低限额，引导其取之于农村的资金，用之于农村。其次，继续深化改革，增强农村合作金融资本实力，提高农村合作金融运行效率，提升农村合作金融支农力度，切实地发挥其支农主力军的初衷。再者，降低在农村地区设立中小金融机构的门槛，吸引更多的金融机构与社会资金进入农村金融市场，构建多层次农村金融体系，更好地适应农村金融需求。此外，因拥有正规金融缺欠的某些优势，非正规金融在农村金融活动中所占比例较高，应借助非正规金融渠道，充分发挥其地缘、人缘与信息优势，规范地增加涉农金融资源供给，助推农村经济社会发展。

2)提高农村生产效率，拓宽农民增收渠道。协整分析显示，样本区间内农村金融规模的扩大与效率的提高不利于农村经济增长，因而，仅仅依赖金融领域的发展和改革难以有效地促进农村经济增长。首先，加大政策性金融与财政支农力度，加强农村固定资产投资与农村基础设施建设，形成和扩大农村资本积累。其次，以能力提升为战略，加强农业科技、金融知识与信息技术的培训，提升农村人力资本。再者，从农村经济本身着手，调整农村产业结构，创新农村产业组织形式，推动农村产业化经营，加大对农村中小企业的支持；发展绿色、体验、休闲、旅游农业等地方特色农业，延伸农业产业链，提高农业的投资报酬率，扩充资金在农村的用武之地，扩大农民的就业机会，扩展农民的收入渠道。最后，继续推进农村土地要素产权制度改革，允许以土地经营权抵押、担保与入股，促使“银根”与“地根”紧密联动；有计划地渐次放开农村市场，允许市民下乡，允许资本下乡，促使劳动力在城乡之间自由流动，加强对涉农工商资本的监管，最终在农村地区形成土地、产业、人才、资金的优化配置与良性循环，提高农村产出效率，实现乡村振兴。

3)完善农村金融信用环境，加强农村金融创新。由于涉农贷款风险高且信息不对称，引起农村资金供需矛盾凸显，农村金融体系难以适应农村经济发展。应加快农村信用体系建设，建立农村信用数据库与信用评级制度，加大违约成本与惩罚力度，形成良好的信用环境，既能够降低坏账发生率，又使得农村金融机构的可持续发展能力得到提升。同时，鼓励各类农村金融机构完善基础设施，扩大互联网的普及与应用，开发涉农投融资产品，创新涉农担保与涉农保险，更好地服务于农村经济增长。