平板微管道内双层流体瞬态电渗流动

卢锦华，石晓君，胡凯燕，邓曙艳

(广东石油化工学院 建筑工程学院，广东 茂名 525000)

微流控芯片的驱动系统经常借助电渗现象输送样本流体，如高分子溶液，或者血液等生物流体[1,2]。电渗流研究是微尺度流动研究的一项重要分支，由早期不同形状的微管道内流动研究[3,4]发展到近几年不同外加环境(如旋转环境[5]、外加磁场)对电渗流动特征的影响规律的研究[6]。随着微机电技术在生物医学等交叉领域的广泛应用，一些微流控芯片需要操作非导电样本，如油质液体等。Brask等[7]首次提出借助导电流体电渗流动带动非导电流体进行传输的双层驱动系统。自此双层电渗流动的研究广受关注。文献[8]研究了平板微管道内已达到稳态的双层电渗流模型。文献[9]考虑液-液界面附近的Maxwell条件下提出了瞬态的双层导电流体电渗流动模型。生物芯片实验室等微流控芯片需要传输、混合或分离导电率较低的样本，导电流体和非导电流体组成的双层电渗流从瞬态到稳态的研究揭示了双层流动电-流场全局发展机理，为微流控芯片内的驱动元件的设计、优化以及精确操作提供一定的理论参考。而平板微管道内的瞬态由导电流体带动非导电流体的电渗流动尚未得到关注。基于此，本文考虑导电流体-非导电流体电渗流动从瞬态到稳态的发展过程，提出相应的控制方程，首先利用拉普拉斯变换法推导了双层速度场解析解，从而掌握了双层系统的瞬态速度分布，其次讨论导电流体电渗特质对双层流动的影响规律，相关结果可以为微流控芯片双层驱动系统的精确控制与优化提供理论依据。

1 数学模型

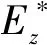
图1 平板微管道内双层不互溶流体结构

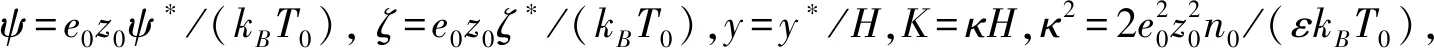
(1)

式中：K、e0、kB、T0、n0和z0分别为电动宽度、基本电荷、玻尔兹曼数、绝对温度、离子浓度和离子价。

电势在平板微管道轴线上满足对称条件，在壁面上等于zeta电势，因此获得如下边界条件：

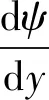
(2)

根据常微分方程解的形式以及边界条件(式(2))，获得式(1)的解，即电势分布如下：

Ψ=[ζcosh(Ky)]/cosh(K)

(3)

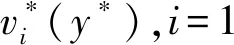
(4)

式中：t、y、v1和v2分别为无量纲化后的时间变量、纵向变量、导电流体速度和非导电流体速度；ρ为密度；U为参考速度；m0为流体黏度。

双层速度和剪切力在液-液界面上满足连续性条件，导电流体速度和非导电流体速度在壁面上均满足无滑移条件，双层流体初始时刻静止，此时，双层速度分布的初边界条件为

(5)

(6)

(7)

根据常微分方程解的形式和边界条件(式(7))，可得式(6)的解如下：

(8)

(9)

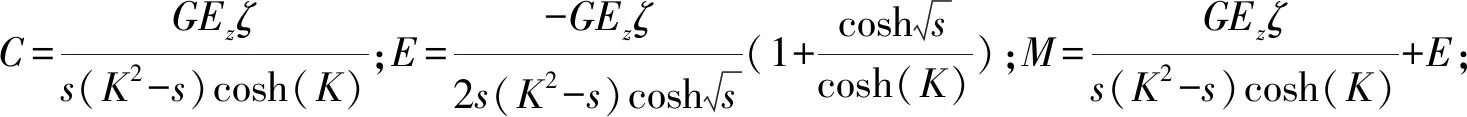
(10)

(11)

式中：P=1,2,…。当时间变量t→∞，式(10)和(11)变为稳态的速度分布，即：

(12)

(13)

进一步合并v1和v2便获得双层电渗流瞬态速度分布v。分别对式(12)和式(13)进行积分，可获得双层电渗流流量Q，即导电流体和非导电流体流量表达式如下：

(14)

(15)

2 结果与讨论

当K=10，ζ=-1时，不同时刻下，双层速度分布以及达到稳态的速度分布如图2所示，其中液-液界面右侧流体为导电流体，液-液左侧流体为非导电流体。当K=100，ζ=-1时，不同时刻下，双层速度分布以及达到稳态的速度分布如图3所示，其中液-液界面右侧流体为导电流体，液-液左侧流体为非导电流体。

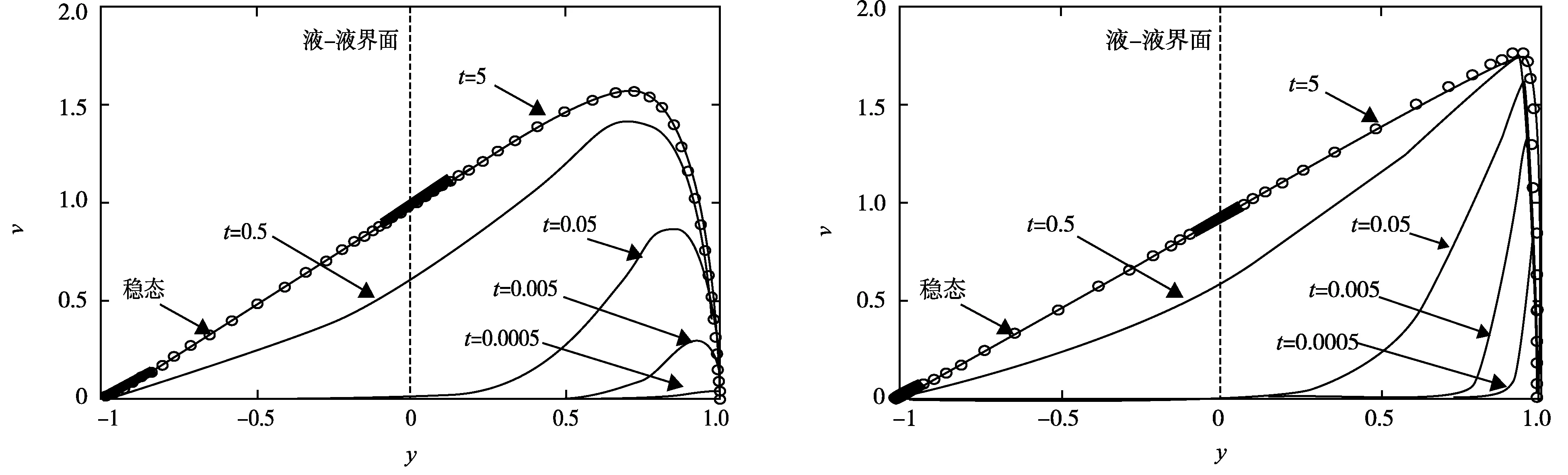
图2 K=10、ζ=-1，双层速度及达到稳态的双层速度分布 图3 K=100、ζ=-1，双层速度及达到稳态的双层速度分布

由图2可知，当时间变量取值相对小的时候，即t=0.0005时，只有壁面附近的导电流体在电渗力的作用下获得速度，随着时间的推进，壁面附近流体带动整体导电流体向前流动；当t=0.005时，导电流体整体处于运动状态，进一步随着时间的推进，导电流体开始带动非导电流体向前流动，如t=0.05时双层速度分布所示。当时间增长到t=5时，瞬态速度与稳态速度重叠，说明双层电渗流当t=5时已经进入稳态，速度分布不再随时间变化。由稳态双层速度分布可知，与单层电渗流相比，由于液-液界面黏性力消耗一部分导电流体动量，双层电渗流不再呈现塞型速度剖面，其中导电流体呈现抛物型剖面，最高速度流层偏向平板微管道下侧壁面，非导电流体呈现线性速度剖面，离导电流体越近的流层，其速度越高。

由图2、图3可知，随着电动宽度K由10增加到100，因管道高度固定不变，故双电层相应地变薄，壁面自由带电离子随之减少，导致导电流体壁面附近的电渗力作用区域变窄，无论任何时刻，紧贴壁面的导电流体速度最高。与图2的双层瞬态速度分布相比，由于电动宽度的增加，导电流体整体获得的速度较高，带动非导电流体向前流动的速度也较高，且导电流体最高速度流层更加靠近平板微管道下侧壁面。

图4为当K=10，ζ=-1时，双层流量Q随时间t的变化趋势，其中Q1为导电流体流量，Q2为非导电流体流量。图5为当K=100，ζ=-1时，双层流量Q随时间t的变化趋势，其中Q1为导电流体流量，Q2为非导电流体流量。

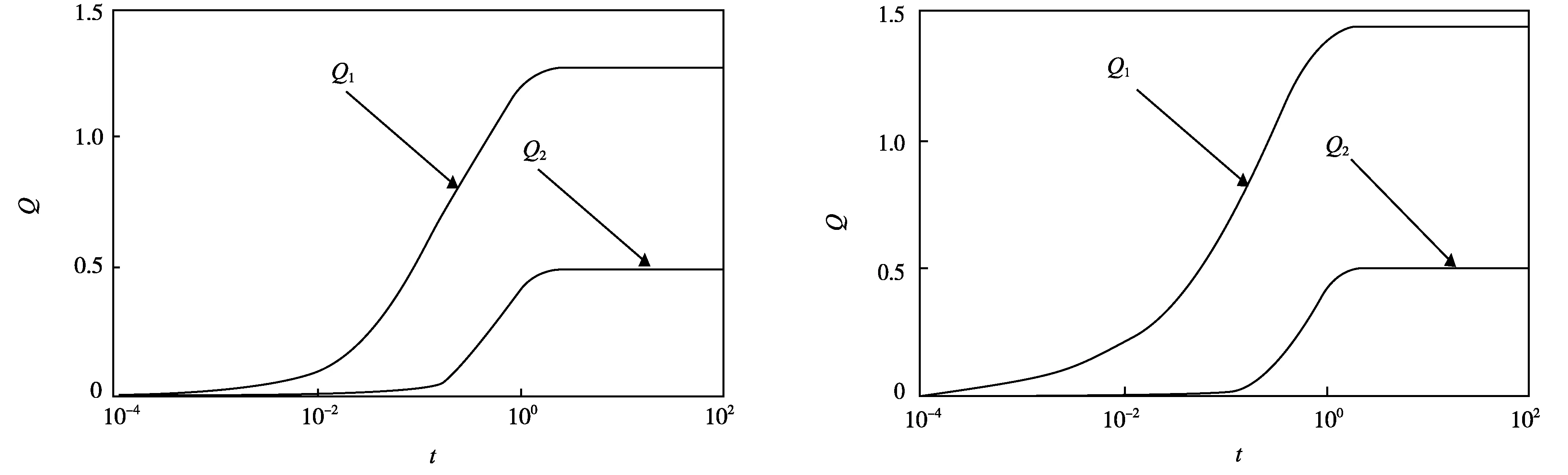
图4 K=10、ζ=-1，导电/非导电流体流量随时间的变化 图5 K=100、ζ=-1，导电/非导电流体流量随时间的变化

由图4可知，导电流体流量和非导电流体流量相比，导电流体更早获得速度进入运动状态，即导电流体在不稳态阶段流动的持续时间较长，而非导电流体在不稳态阶段流动的持续时间较短，更快速进入稳态。无论是导电流体还是非导电流体流动，当时间t达到O(1)时，双层流体开始进入稳态，流量基本不再随着时间发生变化。另外，导电流体流量比非导电流体流量高出好几倍。

与图4相比，图5中导电流体流量显著提高，非导电流体流量变化不显著，导电流体整体获得速度的时间也更早。其解释如下，电动宽度的变化对导电流体流动影响更大，导电流体流动速度峰值明显得到提升，且其速度剖面也有明显变化；而非导电流体流动速度剖面变化不显著，最终导致其流量变化也不显著。

3 结语

考虑平板微管道内瞬态双层流动，下层为导电流体，上层为非导电流体，导电流体在电渗力作用下向前流动，带动非导电流体获得速度，从而形成双层电渗流动，且随着时间的推进逐渐达到稳态。利用拉普拉斯变换法求解了双层瞬态电渗流柯西动量方程，获得了双层速度分布和双层流量。展示了不同时刻的瞬态双层速度分布，发现双层速度分布呈现抛物型剖面，其速度最大值发生在导电流体区域内，偏向管道壁面。讨论了不同的电动宽度下的双层速度分布和流量，发现电动宽度对导电流体流动速度和流量的影响更大。另外，当时间达到O(1)时，瞬态双层流动基本达到稳态。上述结果可以为微流控芯片内双层驱动系统的设计和优化提供理论依据。