求解多右端对称线性方程组的一种极小向后扰动块方法

朱景福，李欣，郭东山

(广东石油化工学院 理学院，广东 茂名 525000)

本文研究多右端对称线性方程组AX=B，其中A∈Rn×n为非奇异对称矩阵；X,B∈Rn×s的数值求解方法。

多右端线性方程组在许多领域都有着重要的应用背景，如控制论、结构力学、电磁场等领域，都涉及多右端线性方程组的求解。多右端线性方程组的求解研究主要有精确解的研究和数值解的研究。在数值解法中常见的迭代法有种子投影方法[1,2]和块迭代法。块迭代法主要有块CG方法(BCG)[3]、块GMRES方法(BGMRES)[4]及其变形、块QMR方法(BQMR)[5]、块EN方法(BEN)[6]、块Lanczos方法[7]等，这些块方法都是建立在块krylov方法[8](krylov子空间方法[9]的推广)的基础之上的。在利用krylov子空间方法求解线性方程组AX=b(即AX=B的右端项矩阵B只有1列)时，通常用残量范数作为判断算法终止的条件。若近似解的精确度比较高，则残量范数较小，反之不一定。为了克服用残量作为算法终止条件的不足，采用极小向后扰动范数代替残量作为算法终止的条件，Kasenally[10]给出了求解大型非对称线性方程组的广义极小向后扰动方法。Cao[11]推广了广义极小向后扰动方法，给出了求解大型非对称线性方程组的总体GMBACK方法。

本文研究多右端对称线性方程组AX=B的右端项矩阵B的列数s>1时的求解方法。新方法在采用块Lanczos方法的过程中结合极小向后扰动技术，讨论AX=B的左端矩阵A的向后扰动形式和极小向后扰动范数的求法，将极小向后扰动范数作为迭代终止的判定条件，提出求解多右端对称线性方程组的一种新算法，并对新算法做残量分析，通过数值对比实验验证新方法的有效性。

1 预备知识

首先给出本文所用到的符号约定如下：本文涉及的矩阵A均为n阶实对称矩阵，λ1,λ2,…,λn为A的特征值，x1,x2,…,xn为相应的标准正交特征向量，并且λ1≥λ2≥…≥λn。En表示n阶单位矩阵，在不产生混淆的情况下用E表示。‖A‖F、‖A‖2分别表示矩阵A的Frobenius范数和2-范数。xT和XT分别表示向量x和矩阵X的转置。νec(A)表示矩阵A的列拉直(列展开)。A⊗B表示A与B的Kronecker积(直积，张量积)。A+表示矩阵A的Moore-Penrose广义逆。

引理1 设A∈Cm×n，则‖A‖F=‖νec(A)‖2。

引理2设A∈Cm×n，B∈Cn×p，C∈Cp×q则νec(ABC)=(CT⊗A)νec(B)[12]。

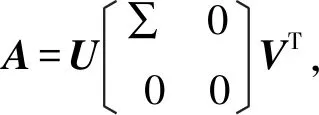
引理4设A∈Cm×n，B∈Cp×q，C∈Cm×q，矩阵方程AXB=C有解的充要条件为AA+CB+B=C，在有解的情况下，AXB=C的通解为X=A+CB++Y-A+AYBB+

(1)

其中Y∈Cn×p是任意的；如果AXB=C无解，则AXB=C的最小二乘解仍为式(1)的形式，并且AXB=C的极小最小二乘解为X=A+CB+[12]。

选取方程组AX=B的初始矩阵X0，并由QR分解得到X0=Q1T1。

块Lanczos方法(BLanczos方法)过程如下[7]：

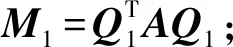
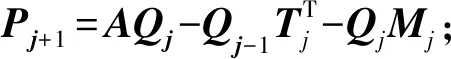
可得

(2)

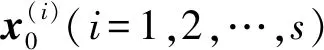
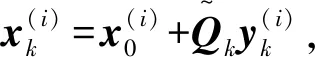
2 极小向后扰动块方法

2.1 向后扰动分析

本文把方程组AX=B的近似解看作向后扰动方程组(A-Δ)X=B的精确解，其中Δ称为AX=B的向后扰动。下面讨论在用块Lanczos方法解方程组AX=B时，考虑把极小化向后扰动范数作为算法终止的判定条件，以克服Lanczos过程产生的特征向量失去正交性的不足，构造求解式AX=B的新算法。

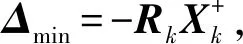
证明：设Xk为方程(A-Δ)X=B的解，则AXk-B=ΔXk所以-Rk=ΔXk

(3)

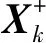
(4)

证毕。

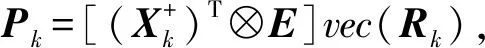
2.2 极小向后扰动块Lanczos方法(BMINBACK方法)

本文以极小向后扰动范数式(4)作为新算法迭代终止的判定条件，给出求解方程组AX=B的极小向后扰动块Lanczos方法(BMINBACK方法)，算法过程如下：

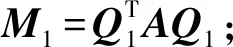
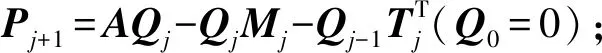
3 数值实验

本文的数值实验均在主频1.8 GHz的酷睿i7CPU、内存8 GB、Win10企业版操作系统的笔记本电脑上采用Matlab R2014a编程实现。

例1 已知对称矩阵

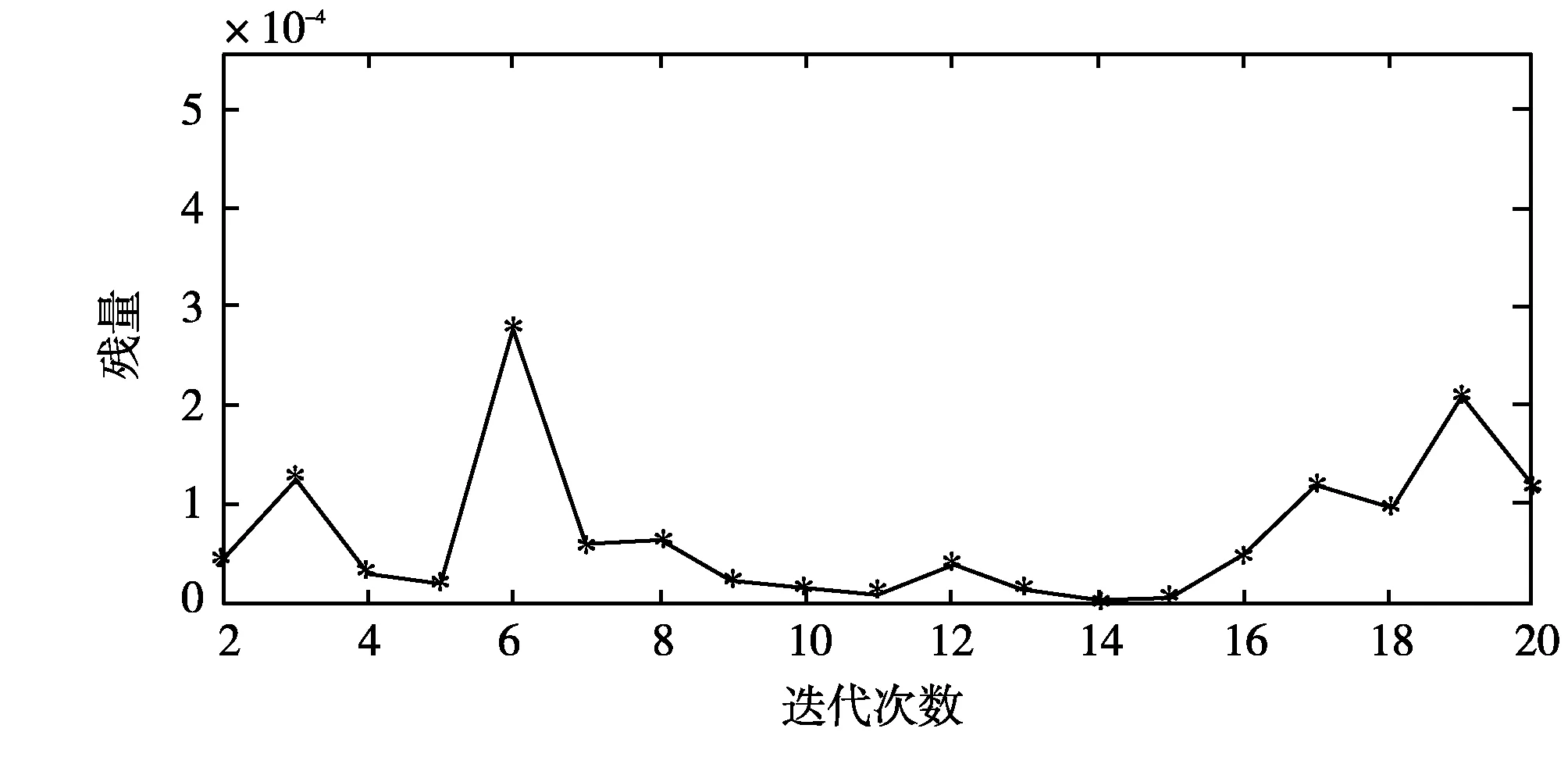
图1 BMINBACK算法残量随迭代次数的变化

由图1可知，采用BMINBACK方法求解方程组AX=B计算的残量达到小数点后5位，验证了极小向后扰动块方法是有效的。

例2 已知矩阵A、多右端项B和初始估计X0(同例1)，当n=100，k=8时，多右端项B的列数s变化时，BLanczos方法和BMINBACK方法的残量结果见表1。

由表1可知，在求解方程组AX=B时，BMINBACK方法计算速度接近BLanczos方法的计算速度，BMINBACK方法的残量略高于BLanczos方法的残量，但BMINBACK方法的执行过程中，采用了极小向后扰动范数作为循环迭代的条件，克服了BLanczos方法采用残量范数作为迭代条件而容易引起算法中断的不足，进一步验证了新方法是有效性的。

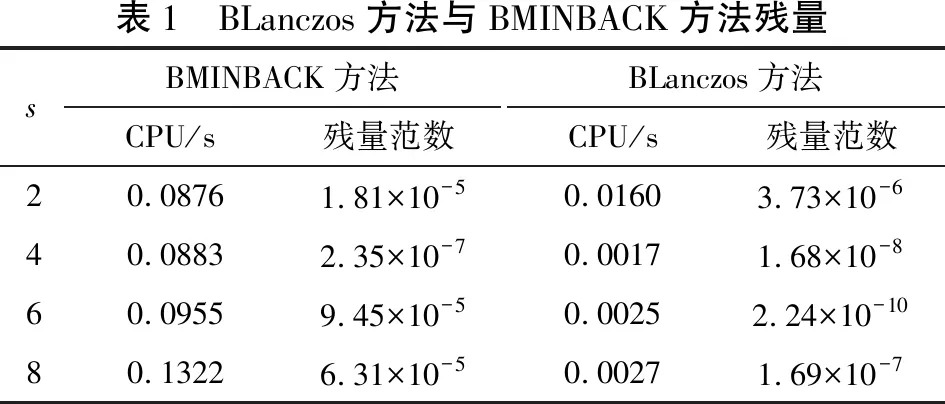
表1 BLanczos方法与BMINBACK方法残量sBMINBACK方法CPU/s残量范数BLanczos方法CPU/s残量范数20.08761.81×10-50.01603.73×10-640.08832.35×10-70.00171.68×10-860.09559.45×10-50.00252.24×10-1080.13226.31×10-50.00271.69×10-7

4 结论

本文提出了求解多右端对称线性方程组的新方法——极小向后扰动块方法(BMINBACK方法)，并对新算法做了残量分析。数值实验结果表明，新算法求解方程组的残量范数达到小数点后5位，在新算法的执行过程中，采用极小向后扰动范数作为循环迭代的条件，克服了BLanczos方法以残量范数作为循环迭代条件而容易引起算法中断的不足。而新方法的残量不是特别小，在满足一定精度的要求下，理论和数值实验说明了新方法的有效性。