基于自适应精英蚁群算法的GM(1,1)预测模型
李 眩,吴晓兵,童百利
(铜陵职业技术学院 经贸系,安徽 铜陵 244061)
20世纪80年代,邓聚龙教授创立了研究“少数据,贫信息的不确定问题”的灰色系统理论,其中灰色GM(1,1)预测模型被广泛应用于工业、农业、经济等领域,是应用非常广泛的一种预测模型.但对于非准光滑数据序列、非平稳的高增长数据序列(发展系数|-a|大于0.5),模型的预测精度不理想.研究学者迫切寻找能提升GM(1,1)模型预测精度的有效方法,他们从GM(1,1)模型的初始值[1]、背景值构造[2]、残差修正[3]、灰导数[4]等多方面进行改进,取得了不少成果.但在模型参数辨识上,传统数学方法始终是存在缺陷,得到的参数并非最优参数,尤其是在预测非平稳数据序列时,传统数学方法求解的参数模型会产生较大误差[5].模型参数直接影响着模型的预测精度,实质上求解GM模型最优参数来提升精度问题是一个优化问题,近年来人类通过模仿生物体进化机制发展起来的人工智能算法完美解决了一些高度复杂的优化问题,为该问题的解决提供了新的思路.考虑到蚁群算法像其他智能算法一样容易陷入局部最优的缺点,本文提出一种信息素浓度自适应调整的精英蚁群算法(ACO算法)来求解GM模型的发展系数和灰色作用量,期望为提升灰色预测模型精度提供一种新的有效方法,并通过实例分析证明该方法的有效性和科学性.
1 灰色GM(1,1)预测模型
GM(1,1)模型是灰色系统理论中最基础的预测模型,在预测形式上属于单数列预测模型,只用到系统行为序列,而无外作用序列,是应用最广泛的灰色系统预测模型.GM(1,1)模型的预测原理是:对某一数据序列用累加的方式生成一组趋势明显的新数据序列,按照新数据序列的增长趋势建立模型进行预测,然后再用累减的方法进行逆向还原,恢复出原始数据序列的预测值.
假设原始数据数列x(0)存在n个观测值,即x(0)={x(0)(1),x(0)(2)…x(0)(n)},将原始数据序列x(0)通过累加生成新数列x(1),以此弱化数据序列的无规律性和随机性以及随机扰动对数据带来的影响.通过累加生成可看出灰量累积过程的发展态势,使杂乱原始数据中蕴含的规律体现出来.
得到新数列X(1)(n)={X(1)(1),X(1)(2)…X(1)(n)},
由X(1)计算其紧邻均值等权新数列Z(1)={Z(1)(2),Z(1)(3)…Z(1)(n)},
其中,Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1).
(1)
对数列X(1),Z(1)建立白化微分方程构建GM(1,1)模型:

(2)
其白化方程为:x(0)(k)+a*Z(1)(k)=b.
(3)
a和b都是模型的待定参数,传统GM模型都是根据数据采用最小二乘法求解参数.
由此可以求出两个方程参数.方程(2)的解如式(4)所示:
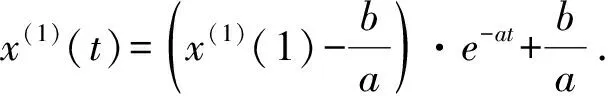
(4)
GM(1,1)模型的时间响应序列为:
将上述结果累减还原,即可得到预测值:
(5)
GM模型的预测精度与模型参数(-a系统发展系数、b驱动项系数)有很大关系,所求参数解是否最优,直接影响到模型的预测精度.有理论分析和实践表明,传统的最小二乘法求解GM模型参数在数据“异常”时会失真较大[6].数据序列变化平稳(发展系数的绝对值<0.5)时,GM(1,1)模型的误差很小,预测效果十分理想;但对于高增长数据序列(发展系数的绝对值>0.5)时,误差很大,做预测都应十分谨慎.
灰色GM模型参数辨识的传统数学求解方法是根据实际值与理论值的误差平方和为目标函数,以其取值最小为目标计算偏导来求解.这样建立的GM模型存在病态性和比较差的鲁棒性,尤其当原始数据序列受到随机扰动影响变化非平稳时,预测值会有较大误差[7].人类通过模仿生物体进化机制使看起来高度复杂的优化问题得以完美解决,为传统优化技术难以解决的优化问题提供了切实可行的解决方案,因此人们转而采取仿生智能优化算法求解模型的最优参数,以此来降低求解参数误差对模型精度的影响,大大促进了灰色理论与信息技术的融合,丰富了灰色系统理论的内涵.因此,本文对蚁群算法进行改进,提出了基于信息素浓度自适应调整的精英蚁群算法,在不改变GM(1,1)模型表示方式的前提下运用其求解GM模型最优参数来提高模型的预测精度.动态自适应精英蚁群算法求解模型参数的基本思想是通过蚂蚁个体在解空间独立搜索,通过信息共享找出群体当前最优解,蚁群在当前最优解的信息素引导下不断迭代进化直至算法收敛寻得最终的全局最优解,其寻找参数最优解的科学性、合理性远胜于传统的数学方法.在此,并通过实际应用结果证明运用动态自适应精英蚁群算法提高GM模型预测精度的合理性和科学性.
2 信息素浓度自适应调整的蚁群算法求解GM模型参数
2.1 蚁群算法(ACO算法)简介
蚁群算法是受自然界蚁群集体觅食行为的启发而诞生的仿生智能算法.蚂蚁个体行为很简单,但由个体组成的蚁群却能完成远超个体能力的复杂任务,他们个体之间通过信息素来相互通讯和进行信息的传递,共同协作完成复杂任务.蚁群有能力在没有任何先行提示情况下找到巢穴到食物的最短路径,并能跟随环境变化搜索新的路径,其中体现了一种信息的正反馈现象:某一路径上走过的蚂蚁越多,该路径上蚂蚁留下的信息素就多,对后来蚂蚁的吸引力就越大,使他们选择信息素强度高的方向移动,蚂蚁个体之间正是通过这种信息的交流而达到搜索食物的目的[8].蚂蚁具有的智能行为得益于其简单行为规则,该规则让其具有多样性和正反馈,在觅食时,多样性使蚂蚁不会走进死胡同而无限循环,是一种创新能力;正反馈使优良信息保存下来,是一种学习强化能力.两者的巧妙结合使智能行为涌现,如果多样性过剩,系统过于活跃,会导致过多的随机运动,陷入混沌状态;如果多样性不够,正反馈过强,会导致僵化,当环境变化时蚁群不能相应调整[9].受蚁群觅食寻找最短路径行为的启发,意大利学者Dorigo等人提出了模仿蚁群觅食行为的蚁群算法,其应用从最初的TSP问题扩展到了网络路由、车辆调度、路线航迹规划及集成电路布线设计等领域,蚁群算法的出现为解决复杂困难的系统优化问题提供了新的求解算法.
人工蚁群算法的蚂蚁个体被表征为优化问题的一个潜在可行解,在众多潜在可行解构成的解空间中根据适应度不断进化迭代,直至算法收敛得到最终的全局最优解.算法体现了蚂蚁觅食行为中的自催化机制,当一个问题的较优解附近聚集的蚂蚁较多,其留下的信息素也就多,根据蚂蚁倾向于选择信息素强度大地方的特点,后来蚂蚁移向该解区域的概率也就越大,反过来又增强了该区域的信息素强度,这种自催化机制利用信息作为反馈,通过对系统演化过程中较优解或较优方案的自增强,使得问题的解向着全局最优的方向不断进化[10].蚁群算法中信息素和真实蚁群一样存在着挥发,使得蚂蚁逐渐淡忘过去,不受历史经验的过分约束,同时基于概率的前进决策策略使其趋向较优区域移动,从而逐步找到问题的最优解或最优方案[11].蚁群算法用于解决优化问题时,信息素是所要优化问题对应解或对应方案优劣程度,其用适应度函数值衡量,算法每经历一次循环,就进行一次信息素的更新,一个有限的人工蚂蚁群体通过信息素指引相互协作、分享信息,既能独立地搜索,又能同时找到很多问题的不同解或不同方案,通过比较找出群体当前高质量的解,逐步进化得到问题的全局较优解或较优方案.
将蚁群算法应用于优化问题的基本思路为:蚂蚁个体表示待优化问题的潜在可行解,整个蚂蚁群体构成待优化问题的解空间.在较优解上蚂蚁释放的信息素量较多,随着时间的推进,较优解上累积的信息素浓度逐渐增高,较优解位置聚集的蚂蚁数量也愈来愈多;较差解上遗留的信息素浓度会逐渐减少最后被遗忘,信息素的挥发机制使得蚂蚁个体在移动的时候不会过多局限于以往蚂蚁留下的历史经验,最终,整个群体中的蚂蚁个体会在正反馈的作用下集中到最佳解上[12].
蚁群算法求解优化问题的实现过程如下:设置好蚁群蚂蚁数Ant、迭代次数T、信息素挥发系数ρ、转移概率阈值P0以及算法的搜索范围(GM模型参数的取值大致范围).模型参数的取值范围(即蚁群的搜索范围)根据具体问题进行适当设定.范围设置过大,算法把搜索范围遍历一次,会降低算法的执行效率;范围设置过小,没有把具体问题的最优解包含在内,会造成算法不成熟收敛或者不收敛,得到的是问题的局部最优解或无解.本文在GM模型参数的求解问题上,在参考传统GM模型近似解的基础上来设置算法的搜索范围,这样有针对性的求解效率会高一些.蚁群算法中蚂蚁个体数量必须根据问题的规模适当设置,太小则不能保证群体的多样性,以致算法性能很差;种群太大尽管可以增加寻优的效率,阻止早熟收敛的发生,但无疑会增加计算量,造成收敛时间太长,表现为收敛速度缓慢.算法对每只蚂蚁位置进行随机初始化,并依据问题定义的适应度函数计算每只蚂蚁对应的适应度值Tau(i),进而比较求出蚁群群体当前最佳适应度值Tau(BestIndex).算法采用以概率为基础的状态转移策略,蚂蚁个体按照以找到解的适应度值计算得来的状态转移概率选择前进的方向,按照下式计算每只蚂蚁的转移概率:
P(T,i)=(Tau(BestIndex)-Tau(i))/Tau(BestIndex),
(6)
其中,T表示当前的迭代次数;i表示蚁群中第i个蚂蚁个体.当蚁群中的单个蚂蚁位置与蚁群中最佳位置相差较远时,蚂蚁转移概率P(T,i)值较大,大于转移概率阈值P0,蚂蚁应该离开当前位置区域去展开全局探索以避免陷入局部最优;当蚂蚁离蚁群当前最佳位置较近,蚂蚁转移概率P(T,i)小于转移概率阈值P0,该蚂蚁则在当前位置邻域展开局部搜索.每只蚂蚁限定在解空间范围内移动,如果超过边界条件,按如下方法处理,这样避免了蚂蚁逃逸出解空间的可能性.
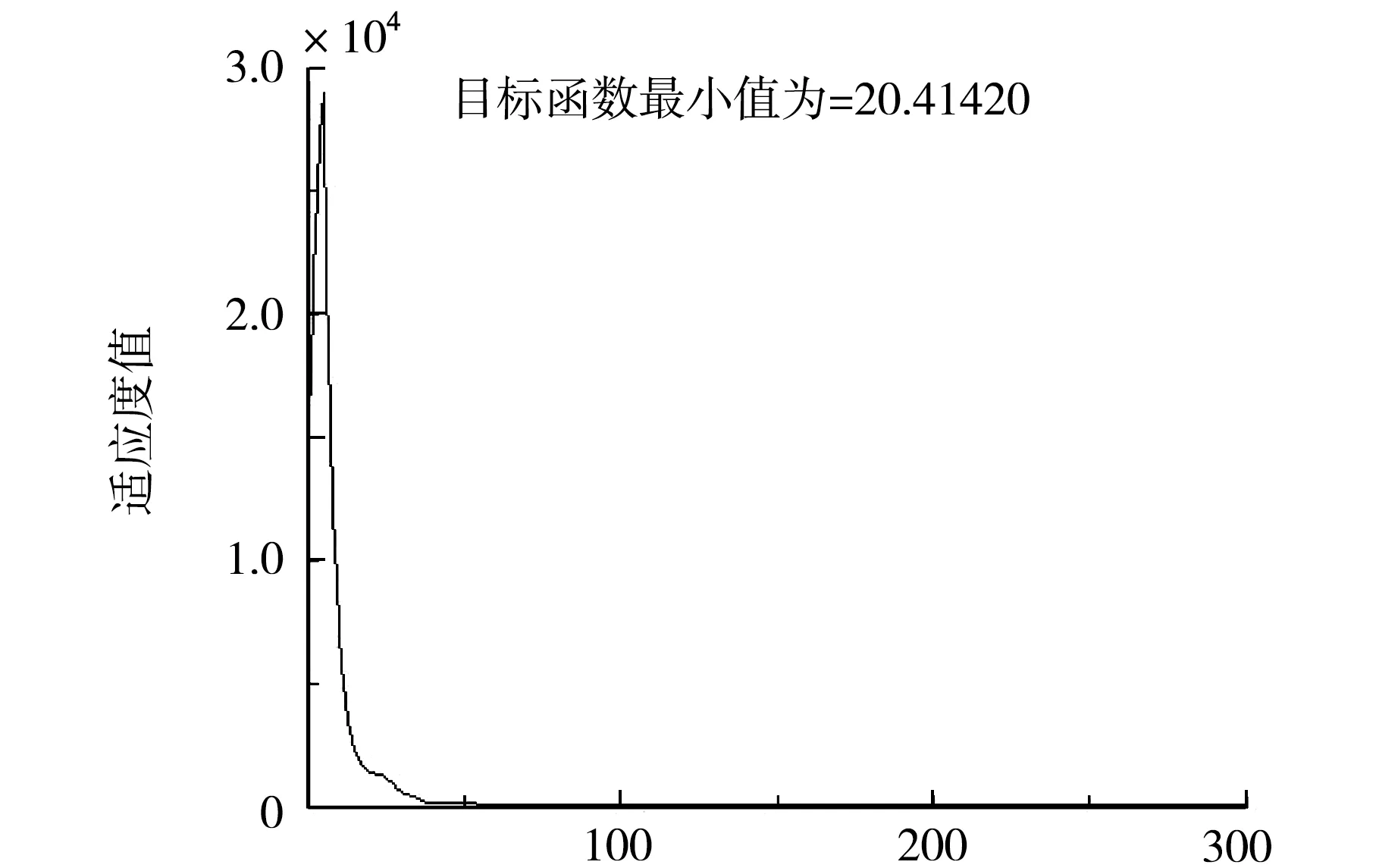
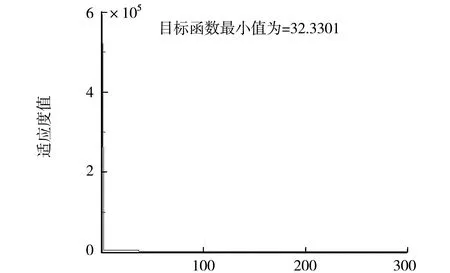
X(i,j)>Xjmax时,X(i,j)=Xjmax,X(i,j) (7) 根据转移概率更新蚂蚁个体的位置、适应度值及其蚁群最优的适应度值,随着时间的推移,如果蚁群找到当前解比原有解较优越,则用当前较优解替换原有解,原有解就会被遗忘;如果当前解比原有解较差,则之前解得到保留,且解的信息量会因蚂蚁留下的信息素得到加强,可行较优解的信息素含量按下式调整: Tau(i)=(1-Rou)*Tau(i)+F(i), (8) 参数Rou表示信息素的挥发度;F(i)为当前循环第i只蚂蚁找到解对应的适应度值.如此不断进化迭代直至算法收敛找到问题最优解.信息素的运用使得蚁群算法具有较强的自我学习能力,可根据环境信息素浓度的变化和过去的行为结果对环境变化进行调整,从而实现算法求解能力的再进化. 随着ACO 算法研究的不断深入,蚁群算法与其他智能方法一样,易陷入局部最优的缺陷逐渐显露,人们开始不断改进蚁群算法提高其算法效率,其中运用自适应策略改进蚁群算法是一个重要的思路.通过自适应改变算法信息素挥发度参数,可以极大保证收敛速度的同时提高全局收敛的能力,当问题规模比较大时,由于信息素挥发度系数的存在,使那些从未被搜索到的候选解的信息量会减少至接近于零,降低了算法的全局搜索能力.另外,当挥发系数较小,较优解留存的信息量比较大,以前搜索过的解被重新选择的可能性过大,也会影响算法的全局搜索能力,通过增大挥发系数,减少信息量的留存可以提高算法的全局搜索能力,但会使算法的收敛速度降低[13].因此在算法陷入局部极值而停滞时,可以自适应增大信息素挥发系数,降低当前局部最优解的信息素浓度,大大降低当前局部最优解被重新搜索到的可能性,使得算法能重新自动搜索其他候选可行解区域,提高算法的全局收敛能力.有助于算法跳出局部极值的束缚,又可以兼顾算法的全局搜索能力和收敛速度.挥发系数的自适应调整方式如下: (9) 其中,Rou()表示信息素的挥发系数;α为自适应调整系数,在此取值为1.15.每次循环后信息素更新规则可表述如下: Tau(i)=(1-Rou(t))*Tau(i)+F(i), (10) 其中,Tau(i)表示蚁群第i蚂蚁找到的解的原有信息素含量;F(i)表示第i只蚂蚁找到该解时对应的适应度值,如果该解质量较优,则值较大,表示解的信息量得到较大的增强. 带精英策略的蚁群算法之所以用精英这个称谓,是因为遗传算法中所使用的精英策略.在遗传算法中,将当前一代中的最适应个体的基因进行突变和重组产生下一代的个体,以此将当前最优个体的优良基因最大限度遗传到下一代中.类似地,精英蚂蚁算法为了使到目前为止所找到的最优解在下一代循环中对蚂蚁个体更具有吸引力,在每次循环后给予最优解以额外的信息素增量,以此来突出该解的优良性,从而扩大精英解和普通解的差异性,使得精英解对蚂蚁个体的引导性增强.精英策略的运用将蚂蚁的搜索行为集中到最优解附近,可以提高解的质量和收敛速度,从而改进算法的性能.按照此策略找到优质解的蚂蚁称为精英蚂蚁.精英蚂蚁算法中信息素的更新规则如下: 如果第i只蚂蚁为精英蚂蚁,找到的解为群体当前最优解,解的信息素按如下方式更新. (10) Tau(i)=(1-Rou(t))*Tau(i)+F(X(i,1),X(i,2)), (11) 从上述解的信息素更新的两种情况来看,精英蚂蚁找到解的信息素含量除按正常方式更新外,还按照解的质量给予其信息素含量一个额外的增强,提高了该解对蚂蚁个体的吸引力.这样使得最优解和普通解的信息素量差异进一步增大,引导蚂蚁的搜索行动向最优解的领域靠近.增强了对蚁群搜索行为的指导性. 蚁群中的每个蚂蚁位置对应优化问题的潜在可行解,根据适应度值进化迭代找到最优蚂蚁则找到了对应问题的最优解.在蚁群算法中用适应度值来评价蚂蚁寻找到的解的优劣,并作为往后蚂蚁个体状态转移和信息素更新的依据,使得随机初始解逐步向最优解进化.由此可见,适应度函数设计是蚁群算法进化寻优的关键. (12) 其中,a,b是待求的GM模型参数,他们是适应度函数的两个自变量. 自变量的取值范围(即蚁群的搜索范围)根据具体问题进行适当设定.范围设置过大,算法把搜索范围遍历一次,会降低算法的执行效率;范围设置过小,没有把具体问题的最优解包含在内,会造成算法不成熟收敛或者不收敛,得到的是问题的局部最优解或无解.本文在GM模型参数的求解问题上,在参考传统GM模型近似解的基础上来设置算法的搜索范围. 程序代码部分删除. 当GM(1,1)模型数据序列变化平缓时,低增长情况下,传统GM(1,1)模型和残差修正模型有较高的精度,模型偏差较小,拟合和预测非常理想,运用蚁群算法优化参数建立的GM(1,1)模型与它们在精度上相差不大,提高效果不显著.当数据序列为高增长序列如指数级增长(发展系数|-a|比较大),尤其是|-a|>0.5时,GM模型精度很差,对使用传统模型以及残差修正模型作短期预测都应该慎重,因此该情况下运用仿生智能算法求解模型参数,提升模型精度十分有必要.下面以指数级高增长数据序列的拟合和预测为例,运用提出的自适应精英蚁群算法改进的GM模型来进行数据的拟合和预测,在精度和误差上与传统模型和残差修正模型进行对比,来验证基GM模型改进的有效性和合理性. 例:某地传染病暴发,在某周感染人数的日报数据如下,x°=[3,11,28,85,251,736,2 199],从数据的变化趋势呈现近似指数级增长.传统GM模型和残差修正GM模型预测结果和误差数据如表1所示,可以看出采用传统GM(1,1)模型和残差修正模型预测误差都比较大,预测效果不理想.仍采用此数据序列的拟合、预测探讨运用智能方法求解模型参数的有效性和优越性. 下面采用基于自适应精英蚁群算法的GM(1,1)模型来对该指数级增长数据序列进行预测,在参考传统GM模型求得参数值的基础上将第1个参数范围(算法搜索范围)设置为[-1.5,-0.6],第2个参数范围(算法搜索范围)设置为[0,2.0],蚂蚁个体数目设为100,迭代次数T设为300,在matlab运行自适应精英蚁群算法程序,得到适应度进化曲线如图1所示,算法收敛相当快.matlab程序求得的GM模型参数分别为:a=-1.090 81,b=1.919 02.得到优化后的GM模型的预测值时间响应式为: 迭代次数 (13) 表1是运用自适应精英蚁群算法与GM融合预测模型对数据序列的拟合预测值、误差值与传统GM模型、残差修正模型的对比. 表1 数据序列预测值及误差 从改进预测模型的拟合值、残差、相对误差和数据变化趋势来看,自适应精英蚁群算法与GM融合模型预测结果非常理想,在原始数据的拟合上误差小,而且在后续时间预测数据的变化趋势与原始数据序列的变化趋势也非常吻合.传统GM模型在指数级高增长数据序列的数据拟合上,误差大,数据变化明显滞后于实际数据的变化,后续时间预测上,预测数据的变化也明显不符合指数级高增长的特征.在数据序列高增长、非平稳变化时,残差修正的应用反而增大GM模型拟合数据的误差,在后续时间的预测数据变化趋势明显大大超前原始数据的增长特征.由此可见传统GM模型、残差修正模型非常不适合指数级增长非平稳数据序列的预测和拟合. 为了验证自适应精英策略用于改进蚁群算法的优越性,在此用该方法求解的GM模型参数与普通粒子群算法、普通蚁群算法求解的GM模型参数在收敛速度、算法运行时间、最终误差等诸方面进行比较,3种算法性能参数如表2所示. 表2 求解GM(1,1)模型的3种算法性能参数 用普通粒子群算法、普通蚁群算法求解的GM模型参数如图2所示.用普通粒子群算法求解模型参数历时最短,但误差最大;普通蚁群算法求解时间稍长,模型误差有所减少,但并非最小,还有改进降低的空间;而自适应精英蚁群算法虽然历时比前两者都长,但求解的结果是最好的,模型总的误差平方和是最低的.由此可见,运用不经改进的智能方法求解模型参数,系统总的误差平方和也明显高于改进后的方法.从一个侧面也反映了运用自适应精英策略改进蚁群算法是成功的,用于优化问题求解具有优越性. 迭代次数 应用结果表明,基于自适应精英蚁群算法的灰色GM模型,对于非平稳高增长的序列,具有较高的拟合与预测精度.对于指数级增长的非平稳序列预测精度提升效果尤为明显.改进后的模型在适用性上较传统模型和残差修正模型具有优越性.同时,与普通的人工智能方法相对比,自适应精英蚁群算法在解决优化问题上,处理能力是较为优秀的. 针对传统求解GM(1,1)模型的参数的局限性,提出了自适应精英蚁群算法求解模型参数的方法.通过应用结果证明文章提出的方法有较理想的预测效果,尤其数据序列变化非平稳时,传统GM模型拟合及预测精度较差的情况,改进的融合模型预测效果非常理想.也同时证明了自适应精英策略改进蚁群算法是合理可行的,比普通智能算法具有较强的优化问题解决能力.自适应精英蚁群算法还可以应用于其他领域的优化问题,具有较广阔的应用前景.2.2 自适应调整和精英策略在蚁群算法中的应用
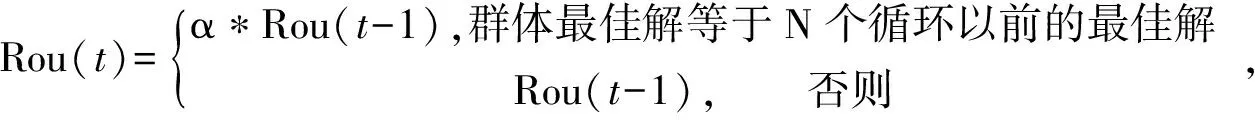
2.3 基于GM(1,1)模型的蚁群算法适应度函数设计
3 改进的蚁群算法与GM(1,1)融合预测模型的实证分析


4 结 论

