一种级间无动力飞行时间在线自适应确定方法

王 智 王 鹏 何 磊

北京宇航系统工程研究所,北京 100076

0 引言

对于直接入轨的固体运载火箭，为满足入轨点参数及控制精度要求，可采用动力飞行/级间无动力滑行/动力飞行的轨迹形式。在动力飞行段之间增加级间无动力滑行段，利用重力转弯减小对动力飞行段的攻角需求，进而改善火箭飞行力热环境，减小入轨点速度损失。

级间无动力滑行段的飞行时间是影响动力飞行段攻角指令大小和入轨点参数及控制精度的重要因素。传统级间无动力滑行时间根据入轨点参数要求离线确定，飞行时滑行结束条件为固定判据，无法根据实际飞行情况进行调节，对干扰的适应性较差。文献[1-3]建立了满足速度矢量和位置矢量约束的制导方法，由于未考虑飞行过程约束以及气动力等因素，上述制导方法在固体运载火箭上升段全段飞行应用中受到一定限制。本文针对固体运载火箭动力飞行/级间无动力滑行/动力飞行的模式，根据火箭当前实际飞行情况、飞行过程约束以及入轨点约束，在线确定级间无动力滑行结束条件，在满足入轨点参数及控制精度要求的情况下，减小飞行攻角和飞行轨迹散布。

1 数值预测制导模型

由于固体运载火箭的动力学模型涉及推力、引力以及气动力等非线性函数，无法直接获取精确的解析解，需要通过数值积分的方式求解微分方程组。因此，采用基于数值预测的级间无动力滑行时间在线确定方法是实现固体运载火箭上升段高精度制导的一种有效途径。

对固体运载火箭级间无动力滑行时间在线确定方法进行研究时，采用瞬时平衡假设：即认为火箭无惯性地转动且控制系统理想工作。

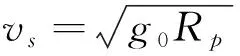
发射坐标系内无量纲化动力学方程可表示为：

(1)

式中，x，y和z为火箭在发射坐标系内的位置分量；vx，vy和vz为火箭在发射坐标系内的速度分量；D和L分别为无量纲化的阻力加速度和升力加速度；ax、ay和az分别为无量纲化的推力加速度在发射坐标系内的分量；θ和σ分别为火箭的弹道倾角和弹道偏角；r为火箭的地心矢径；gx，gy和gz分别为无量纲化的引力加速度在发射坐标系内的分量；aek.x，aek.y和aek.z分别为无量纲化的离心加速度和哥氏加速度在发射坐标系内的分量。

(2)

(3)

式中，ρ为大气密度；v为火箭在发射坐标系内的合速度；Sref为火箭气动参考面积；m为火箭质量；Cx和Cy分别为气动阻力系数和升力系数；Pe为发动机推力；φ和ψ分别为火箭的俯仰姿态角和偏航姿态角。

级间无动力滑行段和动力飞行段的气动力对入轨点参数的影响较为明显，因此在确定级间无动力滑行段时间时需要考虑气动力的影响。为提高计算效率，采用气动力拟合方式引入气动影响。为统一气动力数据拟合表达式，保证拟合形式的一致性，建立式(4)所示的气动力系数拟合函数模型。

(4)

式中，h，Ma，α分别为火箭飞行高度、马赫数和攻角；c0，c1，c2，c3，c0′，c1′，c2′，c3′，c0″，c1″，c2″和c3″为气动力系数拟合系数。

在满足数值预测精度的情况下，为进一步提高数值预测效率，采用式(5)所示的线性化引力模型。

(5)

对于火箭所受的推力，需要区分级间无动力滑行段及动力飞行段过程，推力Pe的表达式为

(6)

式中，PT(t)为火箭发动机高空推力；sm为火箭发动机喷管出口面积；P(h)为火箭飞行高度对应的大气压；thx为级间无动力滑行时间；Ts为级间无动力滑行后动力飞行段的发动机额定工作时间。

2 级间无动力滑行时间数值预测方法

级间无动力滑行时间的长短将直接影响火箭的后续飞行状态。在满足入轨点高度和当地弹道倾角终端约束的情况下，为减小飞行轨迹散布和级间无动力滑行后动力飞行段的攻角指令大小，改善火箭飞行力热环境，通过数值预测方法对级间无动力滑行时间进行在线计算。

在线确定级间无动力滑行时间时，作如下约定：

1)级间无动力滑行段火箭按零攻角飞行；

2)第一次预测级间无动力滑行时间时，假设级间滑行后的动力飞行段火箭按零攻角飞行；

3)第二次及后续迭代预测级间无动力滑行时间时，级间滑行后的动力飞行段攻角在最大值约束范围内，即

|α|≤αmax

(7)

4)级间无动力滑行时间thx在区间[ta,tb]内变化，ta由无动力滑行段结束后的动力飞行段姿态控制起控条件离线确定，tb由入轨点高度约束离线确定。

根据入轨点参数要求，以及状态方程式(1)，级间无动力滑行时间预测模型为

(8)

式中，vf和rf分别为预测的火箭入轨点速度和地心矢径的大小；v0和r0分别为火箭级间无动力滑行开始点的速度和地心矢径的大小。

根据飞行轨迹数值预测方程式(8)和状态方程式(1)，为实现入轨点参数约束，需要确定的变量为级间无动力滑行thx和推力矢量方向xp。由于thx与xp耦合，因此需要迭代计算求解。xp的表达式为

xp=[cosφcosψsinφcosψ-sinψ]T

(9)

在进行级间无动力滑行时间预测时，需要满足以下几点：

1)火箭制导过程处于上升飞行段

为保证火箭制导过程处于上升飞行段，应使得当地弹道倾角Θ不小于0[4-8]。在进行级间无动力滑行时间预测时，首先假设火箭级间滑行后的动力飞行段按零攻角飞行，则在无动力滑行时间迭代区间[ta,tb]内，只要迭代区间两端点对应的后续动力飞行段当地弹道倾角始终不小于0即可，即

(10)

(11)

若式(10)不满足，则在级间滑行后的动力飞行段加入攻角修正，直至满足式(10)要求，进而得到级间滑行后动力飞行段的攻角α0。α0作为后续求解满足入轨点高度和当地弹道倾角约束的攻角初值。

2)入轨点高度约束

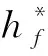
(12)

3)入轨点当地弹道倾角约束

(13)

4)飞行过程中的攻角约束

由于在飞行过程中对火箭的攻角有最大值约束，因此，在进行数值预测时，如果预测出的攻角大于约束条件，则需要对其进行限幅，具体如式(14)所示。

(14)

5)反馈增益系数调节

当引入偏差时，实际飞行轨迹会偏离预测轨迹，此时通过加入反馈环节修正偏差[9-11]。即

φ=φ0+kφ·(θ-θ*)

(15)

式中，kφ为反馈增益系数；θ*为标准轨迹对应的弹道倾角；θ为实际飞行轨迹对应的弹道倾角；φ0为标准轨迹对应的俯仰角。

综上所述，级间无动力滑行时间在线数值预测的流程为：首先对级间无动力滑行时间加以限制，即thx∈[ta,tb]，并通过迭代求解级间滑行后动力飞行段的攻角α0，使得火箭制导过程始终处于上升飞行段，即使得当地弹道倾角不小于0；然后对级间无动力滑行时间thx进行迭代，当级间无动力滑行时间为thxc时，入轨点高度满足约束条件。最后，进一步调整无动力滑行后动力飞行段攻角，使得α=αc时入轨点当地弹道倾角满足约束条件。通过上述运算，得到满足入轨点高度、当地弹道倾角等参数约束的级间无动力滑行时间thxc及攻角指令αc。

通过数值预测得到级间无动力滑行时间后，同步预测得到级间无动力滑行结束点的当地弹道倾角Θ(thx)，飞行控制时，采用Θ(thx)作为无动力滑行结束的判据进行轨迹控制，即满足下式。

Θ(t)≤Θ(thx)

(16)

级间无动力滑行时间数值预测制导流程如图1所示。

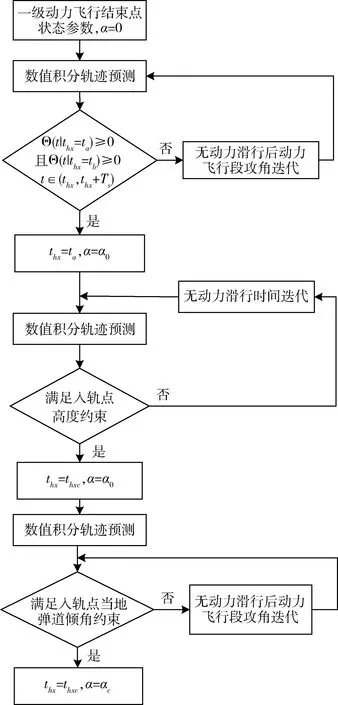
图1 级间无动力滑行时间在线计算流程图

3 仿真分析

采用蒙特卡洛打靶方法分别对传统离线级间无动力滑行时间计算方法和基于数值预测的在线自适应级间无动力滑行时间计算方法对固体运载火箭上升段的控制效果进行了对比。通过分析，在满足入轨点参数精度要求的情况下，基于数值预测的在线自适应级间滑行时间计算方法大幅减小了动力飞行段攻角，缩小了飞行过程高度、当地弹道倾角等轨迹散布，验证了所提方法的有效性。

4 结论

阐述了基于数值预测的固体火箭级间无动力滑行时间在线计算方法，通过仿真分析，获得以下结论：

1)采用拟合气动力和线性化引力等简化措施，在提高轨迹数值积分预测效率的同时，可满足轨迹预测精度的要求；

2)采用基于数值预测的级间无动力滑行时间在线自适应计算方法，在满足入轨点参数精度要求的情况下，对改善火箭飞行力热环境和减小入轨点速度损失有重要作用。通过仿真分析，验证了所提方法的有效性，具有较好的应用价值。