自抗扰fal函数的改进及在无拖曳卫星中的应用
乔鑫宇 周文雅 吴国强
大连理工大学航空航天学院,大连 116024
0 引言
空间科学任务对太空实验环境要求越来越严格,航天器所受到的自身扰动、大气阻力以及太阳辐射等空间扰动成为影响实验结果的重要因素[1-2]。无拖曳卫星以检验质量块作为跟踪点,通过微推进器对卫星本体进行连续主动控制,补偿航天器和检验质量块之间的受摄差,来营造超静超稳的空间实验环境[3-5],在广义相对论的验证以及重力场的测量等领域有着十分重要的应用。但由于空间环境中扰动及噪声复杂,存在极大的不确定性,要想实现其瞬态性能和鲁棒性能的协调控制还存在诸多理论和技术上的困难[6-12]。
由韩京清研究员提出的自抗扰控制(Active Disturbance Rejection Control, ADRC)算法[13]是将控制对象视为积分串联型,利用扩张状态观测器(Extended State Observer,ESO)对动态对象中异于标准型的部分进行实时估计和补偿,来抑制扰动对系统输出的影响。由于算法对参数和结构变化展现出的强自适应能力和稳健的鲁棒性,使其在无拖曳卫星控制器的设计上占据一席之地[14-18]。
作为自抗扰控制器的重要部件,扩张状态观测器的性能直接影响着自抗扰控制器的性能[19-20]。而作为扩张状态器重要组成部分,fal函数直接影响着扩张状态观测器性能的好坏。现有的fal函数在收敛性能上还存在着很大的提升空间[21-22]。为了进一步提升控制器的控制性能,降低残余加速度噪声,本文提出了faln函数,并对其稳定性进行了理论论证,同时与现有的fal函数形式进行比较。
1 模型介绍
无拖曳卫星的工作原理是:通过控制系统保证卫星本体和检验质量块保持相对静止的运动状态。由于检验质量块处于完全保守力环境,从而保证卫星处于 “无拖曳状态”[23-24]。
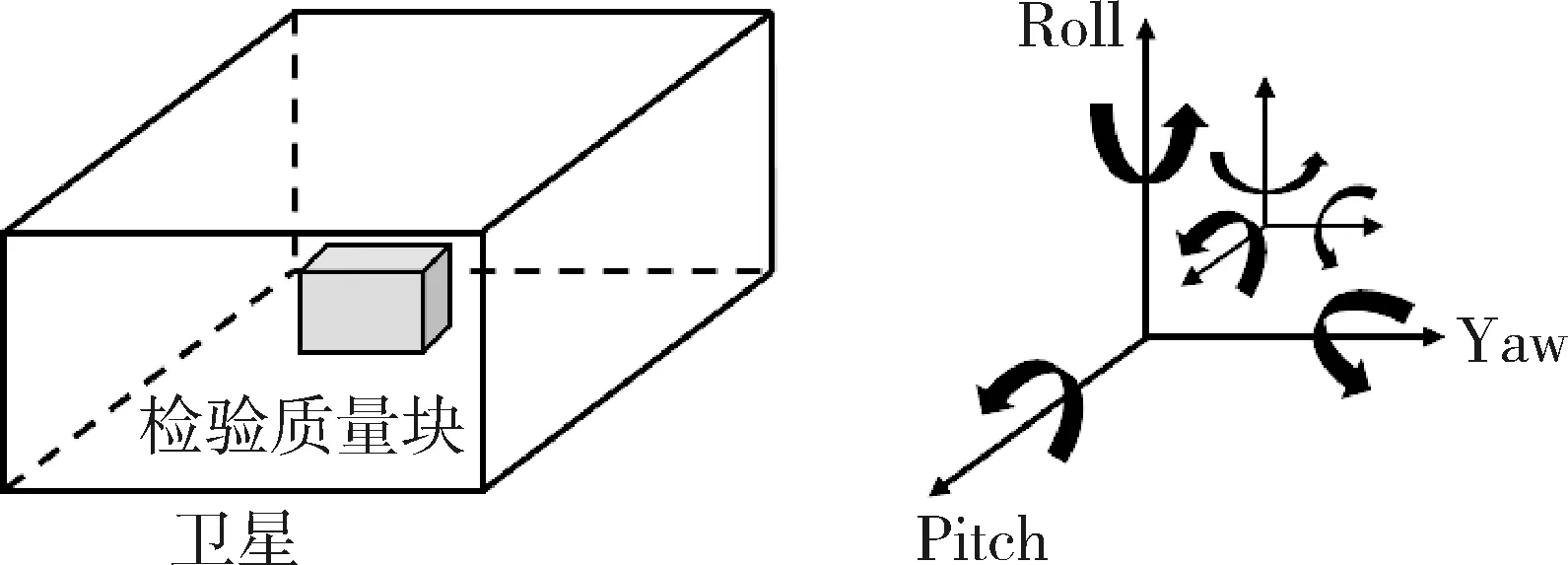
图1 无拖曳卫星控制系统框图
下面给出简化后卫星本体的姿态动力学、相对轨道动力学以及相对姿态动力学模型。
(1)
(2)

(3)
其中,φsc指卫星本体的姿态角,TCsc表示作用在卫星本体上的控制力矩,ωTCsc表示与TCsc对应的输入噪声,TDsc表示作用在卫星本体上的扰动力矩,rrel表示卫星本体和检验质量块间的相对位移,FCsc表示作用在卫星本体上的控制力,ωFCsc表示与FCsc对应的输入噪声,FDsc表示作用在卫星本体上的扰动力,φrel表示卫星本体和检验质量块间的相对姿态角,φtm表示检验质量块的姿态角,TCtm表示作用在检验质量块上的控制力矩,ωTCtm表示与TCtm对应的输入噪声,TDtm表示作用在检验质量块上的扰动力矩,上述介绍的都是在X,Y,Z方向或俯仰(Pitch)、偏航(Yaw)、滚动(Roll)方向上有分量的三维向量;Isc为卫星的惯量阵,Itm为检验质量块的惯量阵,Krot、Drot为卫星与测试质量间的旋转耦合系数,I3为单位矩阵,上述介绍的都是3维矩阵;msc为卫星质量,mtm为检验质量块的质量。
在无拖曳控制中,卫星内部执行机构产生的噪声和卫星的设计息息相关,一般需要其具有很高的精度并同时可以提供相对较大的推力范围。通常为了考虑推力器的未知性能,模型需包含一定不确定性。
2 扩张状态观测器
自抗扰控制器主要由微分跟踪器、非线性组合PID、扩张状态观测器、以及扰动补偿等4部分构成,其结构如图2所示。
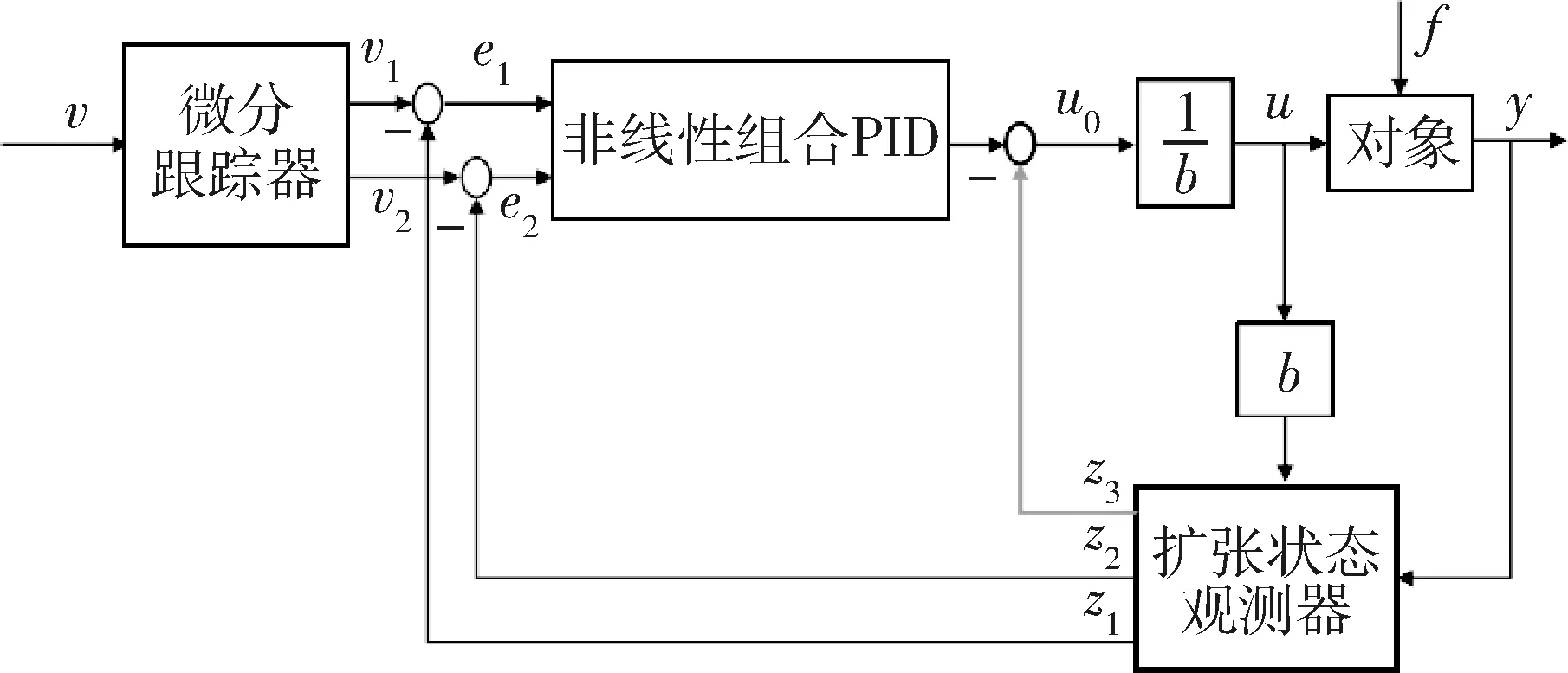
图2 自抗扰控制器框图
微分跟踪器作用是根据控制对象的承受能力安排过渡过程v1并提取设定值v的微分信号v2;非线性组合PID的设计理念是“大误差小增益,小误差大增益”,提升控制效果同时避免执行机构饱和;扩张状态观测器的输出z1,z2和z3是根据输出y和输入信号u对控制对象状态x1,x2以及总扰动x3的估计;最终控制量u是由扰动估计值z3和误差反馈控制量u0共同决定。
传统形式的fal函数是将幂函数改造成在原点附近有线性段的连续非光滑的函数,其表达式如下所示。
(4)
其中,e0是fal0函数变量,一般指的是观测器对输出量的估计误差;a是0~1之间的常数,h是影响滤波效果的常数。这样的非光滑函数形式既可以保证误差快速归于0,也可以避免在误差较小的时候扩张状态观测器的高频震荡现象,在提高控制精度的同时,保证系统稳定性。因此,设计合适的fal函数形式对于提高自抗扰控制器的性能具有深远意义。
3 fal函数的改进
3.1 faln函数
fal0函数并不是在所有应用场合下都具有最优的控制效果[25],众多学者从不同的角度提出了其改进形式。
陈志旺[26]等提出fal1函数形式,并将其应用于四旋翼飞行控制系统。经过仿真验证,系统抵抗外界强干扰的能力增强。
(5)
赵海香[27]提出fal2函数形式。
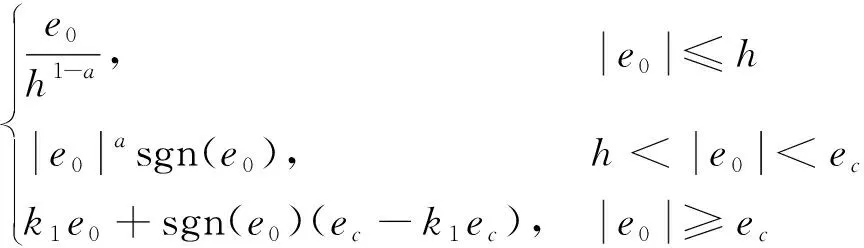
(6)
其中,k1为线性反馈部分的增益;ec是从非线性到线性反馈的误差阈值,可根据实际系统控制量特性以及控制器选取的增益系数进行适当设置。a值越小,非线性段系统反馈增益越小,系统抑制扰动的性能越好。然而,a值的减小会限制系统的控制能力,导致系统误差较大时无法快速有效地利用控制量,最终影响控制系统性能。由于无拖曳卫星的运行环境复杂,不确定性较高,因此需要控制系统具有协调控制性能和鲁棒性能的能力。本文基于指数函数对fal函数进行改进,改进后的fal函数为
faln(e0,a,h)=
(7)
其中,k2为指数项的误差增益,可以根据实际需要进行选取,通常采用较小的正数。
不难发现,相较于现有的fal函数,本文所设计的faln函数增益量适中,以保证在控制系统稳态精度不受太大影响的前提下,尽可能地提高控制系统的收敛速度。
3.2 faln函数稳定性分析
观测器的误差方程为如下形式,
(8)
其中,e是观测器对状态量的观测误差,e1是对状态量x1的观测误差。
本文借助文献[28]所提出的系统稳定性理论来证明使用faln函数的ESO可以完成系统的状态观测。其证明过程借助了如下引理:
引理1如果存在主对角元素为正数的斜对称矩阵D
(9)
使得DA(e1)对称正定,则系统是Lyapunov渐近稳定的。假定d11=1,d22=d33=ε>0以满足主对角线元素为正数的要求。
通过计算计算可得
(10)
其中,
D11=d11β01+d12β02F+d13β03F,
D21=-d12β01+d22β02F+d23β03F,
D11=-d13β01-d23β02F+d33β03F,
那么DA(e1)满足的对称正定性条件如下,
D11=β01+εβ02F+εβ03F>0
(11)
(12)
D11(d12d23-ε2)-2d12ε-d123-d23>0
(13)
其中,B=(β01β02-β03)。
以下需证明存在矩阵D,使上述不定式成立。
由于引理要求矩阵的存在性,因此考虑式(11)成立的必要条件如式(14)所示。
(14)
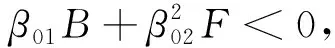
由矩阵的对称性要求可将式(12)和式(13)整理成如下形式。
(15)
β01β02-B>0
(16)
由于B=(β01β02-β03)>0,上式成立。
综上,当D矩阵满足条件B=(β01β02-β03)>0时,可以找到使DA(e1)是对称正定的D矩阵,而系统状态的改变,并不会影响系统的渐进稳定性,由此证明使用faln函数的ESO可以完成系统的状态观测。
4 仿真试验及结果
4.1 无拖曳卫星faln自抗扰算法验证实验
为了验证设计的控制系统对于外界扰动的补偿效果,分析系统的控制精度,对系统进行仿真实验。系统模型(1)~(3)中的参数取自文献[23]-[24],具体设定如下文表述以及表1所示。

表1 卫星仿真参数
假定ωTCSC和ωFCSC的功率谱密度均为10-8m·s-2·Hz-0.5,ωTCtm的功率谱密度为10-15m·s-2·Hz-0.5,干扰力与力矩具有正弦性质,频率为ωd。
本文从卫星本体和检验质量块的相对位置、相对姿态等方面对这两种方式进行比较。
4.2 数值仿真
无拖曳卫星在运行过程中可能会受到来自环境的大幅度干扰或者需要采取主动位置姿态调整,这两种情况都会导致检验质量块和卫星本体出现瞬时位置和姿态偏差。此时扩张状态观测器的状态估计误差瞬时变大,fal函数大误差段的函数形式会直接影响状态估计性能。
综上所述,本文重点分析偏差后卫星本体和检验质量块的运行状态以及扩张状态观测器的状态估计情况,说明本文提出的faln函数在无拖曳卫星控制方面的优势。不失真实性和一般性,假定卫星本体和检验质量块相对距离初始值为rrel0=[0.1 0.3 0.2]Tm,相对姿态角初始值为φrel0=[0.1 0.3 0.2]Trad。
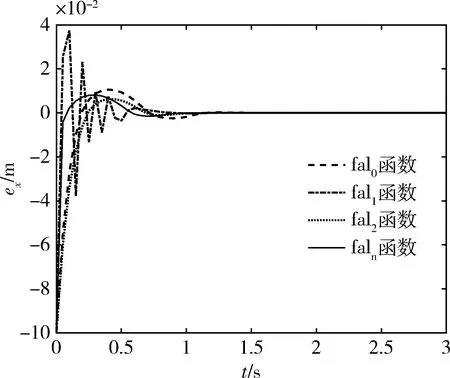
图3 x轴相对位置观测误差曲线
上图给出的是4种ESO对于x轴的相对位置rx的观测误差曲线,可以直观看到基于faln函数的ESO具有更快的观测误差收敛速度和更加平稳的收敛过渡过程。
实际上,fal1函数以牺牲控制性能保证控制系统的鲁棒性,然而无拖曳卫星质量较大且运行时所受环境扰动相对于大气环境较小,因而其优势无法得到体现,在相对位置和姿态仿真曲线中收敛速度较慢,甚至出现发散情况。因而本文主要针对基于fal0、fal2和faln的控制器性能进行比较。
图4和5给出的是卫星本体和检验质量块的x轴相对位置rx及pitch轴相对姿态φpitch的数值仿真情况,其他两轴的位置姿态调节曲线与其类似,本文不再给出。仿真结果显示,基于faln函数的控制器收敛速度最快,能够实现最快速的三轴相对位置和姿态稳定。
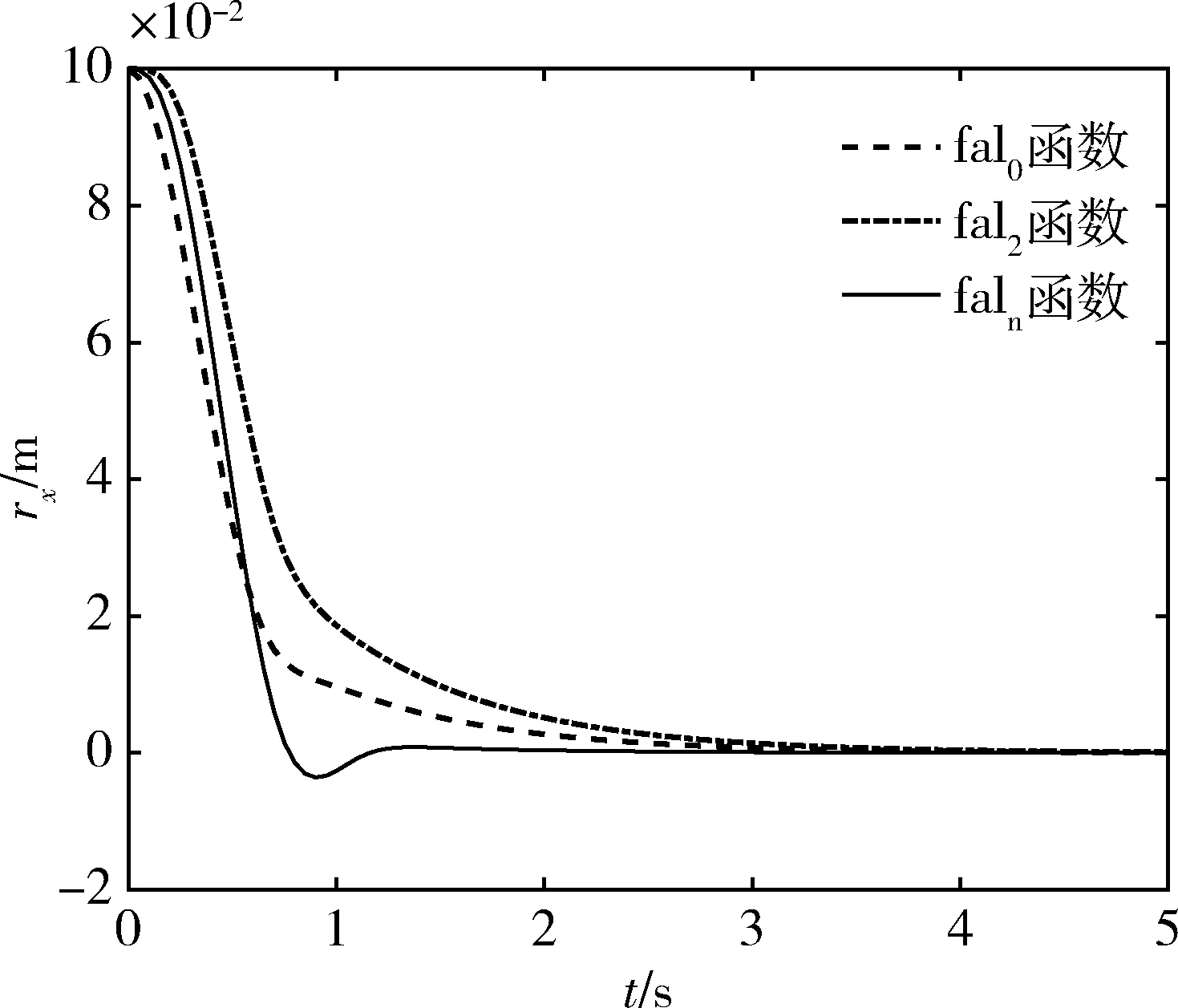
图4 x轴相对位置变化曲线
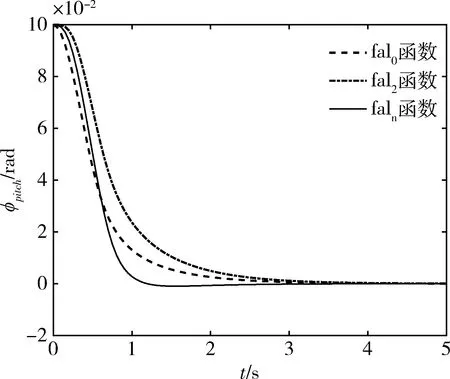
图5 Pitch轴相对姿态变化曲线
图6给出的是基于faln函数的无拖曳控制系统三轴线性残余加速度功率谱密度的拟合曲线。其中z轴达到10-13m·s-2·Hz-0.5量级,x和y轴能够达到10-14m·s-2·Hz-0.5,在数值仿真实验上,能够和LISA-Pathfinder达到相同水平。
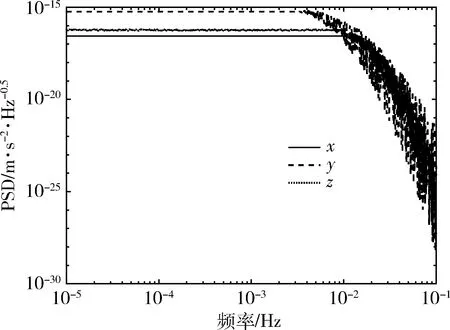
图6 卫星和检验质量块线性残余加速度功率谱密度
以上仿真结果证明了基于faln函数的无拖曳控制器在保证卫星稳定运行的情况下,提高了ESO的观测性能,同时缩短了无拖曳卫星位姿调整时间,加快了控制系统运行效率。
5 结论
本文的研究重点在于如何通过改进自抗扰fal函数,来提高扩张状态观测器对无拖曳卫星的位姿状态的观测能力,从而使无拖曳控制系统控制过程更加平稳、快速。基于此目标,本文提出了faln函数。在通过数学理论证明其稳定性后,完成了与现有的fal函数形式的对比分析。数值仿真实验证明基于faln函数的无拖曳控制器具有更好的状态估计性能和更快速更稳定的过渡过程,更适用于无拖曳卫星的位姿控制。
接下来的首要工作是如何进一步改进状态观测器的状态估计性能,使得误差曲线更加平滑。此外,目前大部分的fal函数改进算法侧重于大误差段的函数改进,无法改进控制系统的稳定状态。如何设计出一种更大范围的fal函数改进形式,使其具有更好的稳态性能。对于提升自抗扰控制器的控制性能具有十分重要的意义。

