基于深度强化学习的高速飞行器攻防博弈

何湘远 尘 军 郭 昊 余卓阳 田 博

空间物理重点实验室，北京 100076

0 引言

高速飞行器以其飞行速度快，变轨能力强而受到世界各军事大国的广泛研究[1]。机动突防是高速飞行器一种有效的突防手段[2]。传统程序式机动由于手段较为固定，未能根据拦截弹实际情况有的放矢，因此突防效果欠佳，存在一定的局限性。微分对策是近些年发展较快的一种智能突防方法，与传统程序式机动策略相比，兼具实时性与智能性[3]。文献[4]将脱靶量和能量消耗作为EKV与弹头对抗指标，考虑弹头机动过载和控制变量约束，建立了该方法下的突防决策模型。文献[5]将弹道导弹拦截问题描述为二人零和微分对策模型，并得到了在捕获区无论突防弹采取何种策略都将被拦截，反之在逃脱区突防弹采取最优策略则必定突防成功的结论。文献[6]考虑在目标有防御器时的三星博弈场景，采用博弈切换策略将其分解为分段双星博弈，使得拦截器在不被防御器反拦截的情况下实现对目标的快速拦截。文献[7]设计了一种基于状态相关Riccati方程的微分对策制导率，得到的结果优于经典微分对策。针对经典微分对策计算量较大的问题，文献[8]将深度神经网络与微分对策相结合，采用经典微分对策生成样本用于训练，生成的机动策略与传统策略基本一致，且兼具较好的实时性。

深度强化学习是近年兴起的人工智能领域中的研究热点，并在例如游戏博弈[9]、机器人控制[10]、制导控制技术[11]当中取得了十分惊人的效果。2013年谷歌DeepMind团队提出了Deep Q-learning算法，该算法也被视为是第一个深度强化学习算法[12]。文献[13]提出了一种改进的DQN算法，被称之为双重深度Q网络算法(DDQN)。该算法很好的缓解了DQN在采取最大化操作时造成的Q值过估计问题。深度强化学习的发展为高速飞行器机动突防提供了一种新的解决方案。深度强化学习以其能够处理高维抽象问题，且可迅速给出决策[14]等优点，有望被应用于攻防博弈决策控制中。文献[15]对经典DQN进行了改进，设计了一种深度神经网络架构竞争双深度Q网络(D3Q)，实现了对弹道导弹中段突防最优控制模型的逼近。文献[16]利用深度确定性策略梯度算法(DDPG)对巡飞弹突防控制决策进行了求解，并验证其有效性。文献[17]以智能小车追逃来模拟导弹攻防过程，在二维平面上采用经典DDPG算法实现了智能小车的控制，并能够较好地完成追捕任务。面对经典DDQN算法随机均匀抽样易忽视罕见且具有高学习价值样本的问题，文献[18]提出了基于时序差分误差(TD-error)的优先经验回放技术，有效提高了学习过程中的样本利用效率。文献[19]提出了基于累积回报值的优先级经验回放方法。然而高速飞行器攻防博弈场景动作空间和状态空间维度大，非线性强，以TD-error计算优先级时优先级较高的往往是对抗转移至终端状态时刻的样本，这使得智能体容易过多关注临近结束时的策略学习而缺乏对其余样本的学习。而以奖励值计算优先级容易使智能体过多关注成功样本，训练样本缺乏多样性。

针对上述问题，本文设计了一种基于经典DDQN的改进算法，通过结合累积奖励值与累积TD-error，采用模糊推理将一轮对抗样本整体存储至不同经验池中，并通过积分抽样器从中抽取样本进行学习。仿真结果表明，该方法能有效提高智能体对样本的利用效率。

1 攻防对抗模型

1.1 攻防对抗场景

一对一突防是一种典型的攻防对抗场景，本文考虑逆轨拦截，建立地面坐标系odxdydzd下的拦截器与飞行器的三自由度运动模型，其示意图如图1所示：

图1 攻防对抗示意图

拦截器在初始状态下飞向预测交会点，由于对抗过程时间较短，为简化模型，预测交会点由飞行器和拦截器在零控状态下按照匀加速直线外推得出。

拦截器采用4台液体轨控发动机进行机动，其推力为2300N，比冲2900N·s/kg，拦截器横纵向导引率采用的是真比例导引，其制导指令分别为：

(1)

其中,导引系数ky=kz=4，突防成功判据为脱靶量Rf>3m。

2 攻防博弈决策算法

2.1 MDP决策控制模型

马尔科夫决策过程(Markov Decision Process，MDP)是强化学习的基础，其决策过程如图2所示：

图2 马尔科夫决策过程

MDP一般由五元组表示[18]，其中,S为状态空间，A为动作空间，P为状态转移概率，R为奖励函数，γ为折扣因子。

在本文中，状态转移由攻防双方动力学方程唯一确定，因此可认为状态转移概率P为1。飞行器需要不断通过与拦截器对抗，并从中获取经验和奖励，用于改进自身策略，以达到成功突防并减少自身机械能消耗的目的。

1)状态空间设计

状态空间应尽可能完整地描述攻防双方的位置、运动特征以及自身的飞行状态等关键信息，而攻防对抗往往更关注的是其相对运动信息，用相对参量代替绝对参量能够减少状态空间维度，提高模型训练效率，这里设计状态空间为：

(2)

2)动作空间设计

由于DDQN的动作空间是离散的，因此需要将飞行器原本连续的动作空间离散化。高速飞行器气动外形一般为面对称结构，主要通过控制攻角和倾侧角完成机动。若直接将指令攻角、指令倾侧角离散，则会导致动作空间随指令攻角、指令倾侧角的细分而过于庞大，给动作搜索带来困难。且受限于飞行器姿控系统能力，将有大量动作因超出控制系统阈值而等效。无法体现出不同动作的差异性，给模型的训练带来困难。因此这里设计动作空间为：

(3)

即在某时刻，指令攻角和指令倾侧角可选择增加、不变或减少其在决策周期内调姿能力的最大值。这样随着决策周期缩短，攻角和倾侧角曲线将逼近真实曲线，且动作空间维度不变，避免了动作空间过于庞大的问题。

3)奖励函数设计

强化学习的核心概念是奖励，强化学习的目标是最大化长期的奖励[20]。一个良好的奖励函数应能正确反映设计人员的目的，且能够给予智能体正确的引导，避免智能体仅关心奖励值，却违背设计人员预想目标的“奖励黑客”问题[21]。对于进攻方，其目的主要有2个：1)成功规避拦截器的拦截；2)在目的1)的基础上尽可能减少自身躲避机动时的机械能损耗。因此设计人员只关注其对抗结束时的终端状态，但若只引入终端状态下的奖励，则会导致奖励过于稀疏，且训练时不能给智能体以正确的过程引导，给智能体训练带来极大困难。因此这里设计奖励函数为：

(4)

即奖励函数由过程奖励rc和终端奖励rf组成，过程奖励包括决策周期内拦截器燃料消耗Δmm和飞行器机械能损失ΔEt，km和kt为比例因子。终端奖励包括突防失败和成功2种情况：若突防失败，则奖励值为-10，若突防成功，则奖励值为10+log2(Rf-2)，其中Rf为脱靶量。这里引入脱靶量奖励是为给智能体训练进行引导，让其适当追求较大脱靶量。

2.2 DDQN损失函数

DDQN(Double Deep Q Network)是DQN的一种改进算法，其通过改进损失函数解决了DQN出现的过估计问题[13]。在DQN中，损失函数计算如下：

(5)

即DQN对动作的未来价值由状态st+1下目标网络计算所有动作中Q值最大值来评价。而DDQN将损失函数修改为：

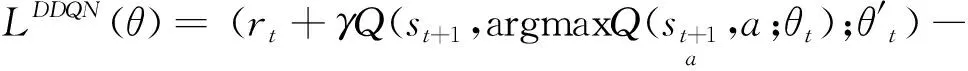
(6)

即DDQN在评价状态-动作值函数时不再用参数为θ′的网络计算最大Q值，而是用参数为θ的网络选取动作，用参数为θ′的网络评估状态-动作值函数。

2.3 样本模糊推理模型

在攻防博弈问题中，样本Q值的TD-error和样本奖励值均可评价样本的重要程度。TD-error越大的样本意味着神经网络所拟合的Q值误差越大，也就越值得学习。DDQN算法的TD-error计算如下：

(7)

定义样本的优先级为：

pi=|δt|+ε

(8)

其中，ε为一非零小量，以保证TD-error为0的样本也有概率被采到。

样本的优先级虽然一定程度上体现了样本的重要程度，但以TD-error评价样本优先级时忽略了奖励值对智能体的作用。并且在飞行器攻防博弈场景下，优先级较大的样本往往是飞行器转移至对抗终端时刻的样本，而攻防对抗过程早期所采取的策略对终端状态有较大影响，因此仅以TD-error为标准进行抽样会使智能体过多关注对抗结束时刻的策略。而好的策略在对抗初期虽然奖励值较小，优先级较低，但依然拥有较大学习价值。奖励值虽也可用于评价样本重要程度，但若单独依靠奖励值评价样本，又会使智能体仅关注突防成功的样本，学习样本缺乏多样性。

针对上述问题，本文将一次对抗的所有样本作为一个完整单元，以一个单元的累积奖励与累积TD-error作为模糊推理的输入，并依靠模糊推理评价该单元样本的好坏程度。

模糊计算过程可以划分为模糊规则库、模糊化、推理方法和去模糊化4个部分[22]。根据仿真经验，设计奖励值对应论域为[-0.5，1]，TD-error对应论域为[0,1.2],本文设计隶属度函数为如图3所示，其中{PS，PM，PN}分别对应模糊标记{正小，正中，正大}。

图3 输入值与输出值隶属度函数

根据累积奖励与累积TD-error所计算出的隶属度，需要根据专家经验建立模糊推理规则表。根据仿真经验，本文设置模糊推理规则如下：

表1 模糊推理规则

表中采用IF-THEN模糊规则得到模糊集到输出之间的关系：

(9)

去模糊化过程是将模糊值转换成精确值的过程。本文通过最常用的面积重心法来实现去模糊化，即样本价值越高，其存储在经验池1中的概率越大。一个单元的经验存储至经验池1的概率为：

(10)

通过式(10)，可以得出一个单元样本存储至经验池1中的概率，样本存储至经验池2的概率计算过程与之类似。这样就实现了样本分类存放的目的。

2.4 积分抽样器

通过模糊推理实现了将样本进行分类存储的目的，但以固定概率从这些经验池中抽样会导致智能体难以根据训练过程调整学习的重点。训练初期由于尚未形成稳定的策略，因此应该保证训练样本的多样性。而训练后期由于策略已初见端倪，智能体应该更多关注那些罕见且高价值的样本，用于进一步改进自身策略。因此本文设计了一种积分抽样器，对累积奖励的时序差分误差进行积分，用于判断智能体策略是否已经形成，并调整从不同经验池中抽样的概率，进而调整智能体的学习重心。定义第τ轮对抗的累积奖励时序差分误差为：

(11)

则抽样器从经验池1中抽样概率为：

(12)

其中，P为经验池1与2抽样的概率之和，为一常值，kI为积分系数。为避免从经验池1和2中抽样过多引起过拟合，设置总经验池用于保存对抗过程中的所有样本，并保证抽样器以1-P的概率从总经验池中抽取样本，以保证抽样的多样性。图4给出了改进DDQN的算法框图。

图4 改进DDQN算法框图

3 仿真试验及结果

3.1 仿真参数设置

实验在python3.6+tensorflow2.4环境下运行，设计神经网络为包含3个隐含层的全连接神经网络，隐含层结构为512×256×128，激活函数选择Leaky-relu函数，神经网络学习率η=0.00001，折扣因子γ=0.9，经验池1大小为D1=1000，经验池2大小为D2=2000，总经验池大小为D3=5000，样本批大小minibach=32。

为提高模型的泛化能力，防止模型过拟合，这里令攻防双方的初始参数分别在各自区间内随机生成，飞行器初始参数如表2所示：

表2 飞行器初始参数

拦截器初始参数如表3所示：

表3 拦截器初始参数

3.2 实验结果及分析

对智能体进行10h训练，共完成约25000轮对抗，图5展示了训练过程中每100次对抗平均突防概率的变化情况，图6展示了每100次对抗平均累积奖励值变化情况。可以看出，经典DDQN算法与改进DDQN算法均能有效处理飞行器与拦截器的攻防博弈问题，训练后平均突防概率均提升至95%以上。

图5 平均突防概率随回合数变化

图6 平均累积奖励随回合数变化

智能体在训练初期由于采用随机搜索策略，对抗中存在大量突防失败经历，突防概率和奖励值较低，此时智能体还未形成较好的策略。随着训练的进行，智能体随机搜索的概率逐渐下降，突防概率和奖励值也呈现上升趋势，说明智能体能够不断从对抗过程中学习并改进自身策略。

相比于经典DDQN算法，改进的DDQN算法能够收敛于更高的平均累积奖励值，说明改进DDQN算法搜索到了更优的策略，能以更小的机械能损耗完成突防。

训练前攻防双方的飞行轨迹由图7给出，此时智能体由于还未形成稳定策略，机动后仍然被拦截器所拦截。

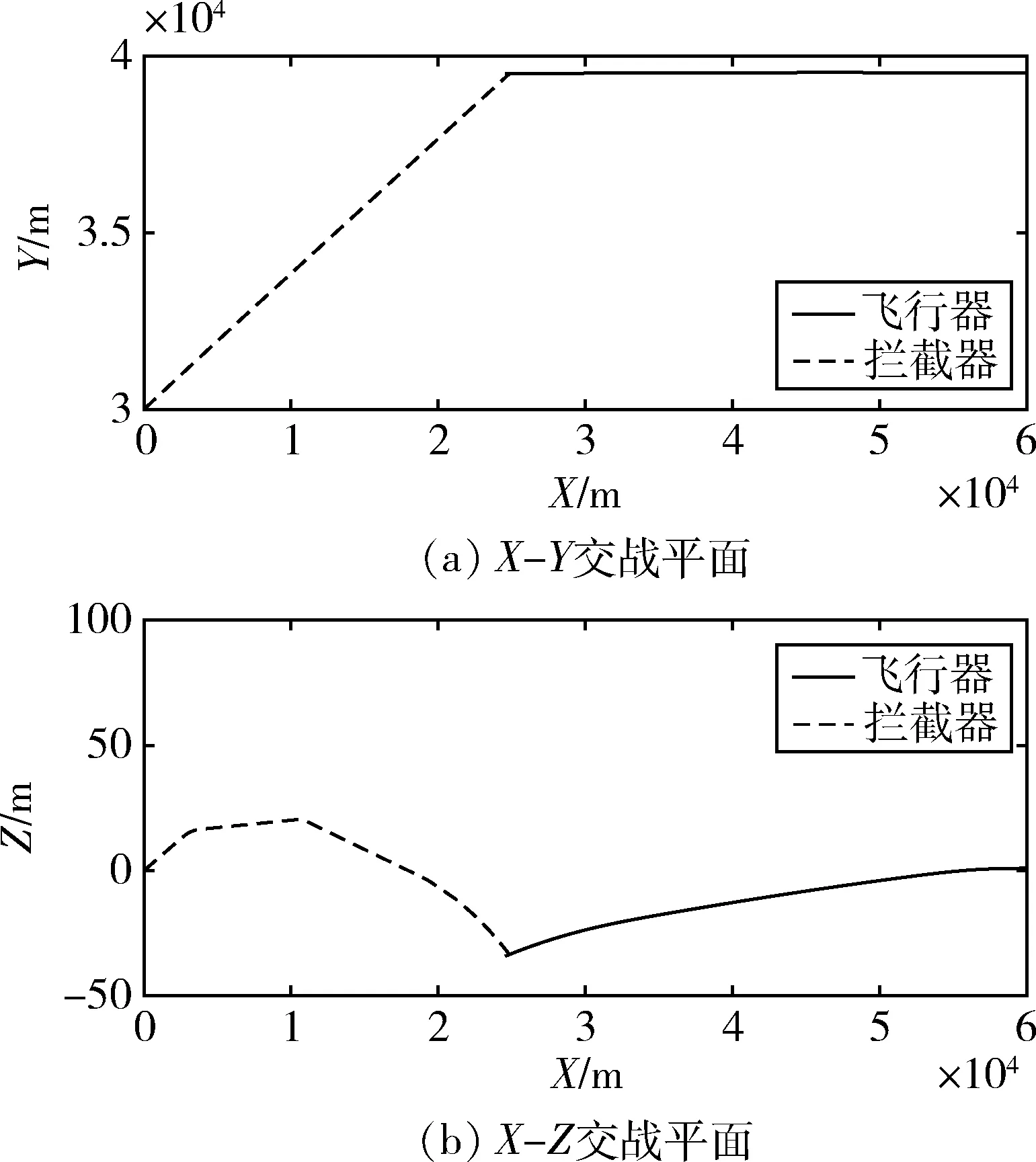
图7 训练前攻防双方飞行轨迹

图8给出了训练后的攻防双方飞行轨迹。可以看出，初始状态下拦截器飞向预测碰撞点，飞行器不断机动以躲避拦截器的拦截，同时拦截器在比例导引作用下修正自身轨迹，最终飞行器以12.7m脱靶量完成突防。

图8 训练后攻防双方飞行轨迹

图9展示了飞行器攻角和倾侧角变化情况，智能体所采取的策略是在对抗初期采取小攻角飞行以节约自身能量，随后在2.4s时开始不断加大攻角直至28°，同时倾侧角继续旋转至100°左右，以类横向机动进行飞行，迫使拦截器大量消耗自身燃料以调整轨迹。在6.5s时再次减小攻角降低自身能量消耗，最终在7.9s完成该次对抗。

图9 飞行器控制指令曲线

4 结论

针对高速飞行器攻防博弈决策控制问题，提出了一种基于DDQN的改进算法。该算法针对样本回放过程，利用模糊推理评价样本好坏程度并分类存储，再根据训练过程中的累积奖励时序差分设计了积分抽样器，根据训练过程调整抽样的侧重点。结果表明，改进DDQN算法收敛时平均累积奖励值高于经典DDQN算法，该算法能够使智能体不断学习并改进自身策略，训练后平均突防概率高于95%，且在成功突防的前提下减少了自身的能量消耗，形成的策略符合设计人员的预期。这为解决高速飞行器攻防博弈决策问题提供了一种新思路。