一种基于动态逆-滑模的变形飞行器姿态控制方法研究
郭嘉宝 赵长见 宋志国
中国运载火箭技术研究院,北京 100076
0 引 言
变形飞行器是一种全新概念的多用途多形态飞行器,能够根据飞行环境、飞行剖面和作战任务等的需要进行适应变形,以发挥飞行器最优的飞行性能。近年来随着各种先进技术的发展,如智能材料、传感器、机电系统、气动和控制等技术的进步,以及人们对飞行器灵活性、机动性、多功能和高效能等需求的不断提高,变形飞行器已成为现代高性能飞行器的未来发展方向之一,具有极大的研究价值和应用潜力。
与现有的固定式布局飞行器相比,变形飞行器最突出的特点是其变形能力。飞行器的变形会带来展长、翼面积、后掠角、展弦比、质心位置和转动惯量等结构参数的变化,还会引起飞行器气动特性和动态特性的非线性变化[1-3],这些都对飞行器的姿态稳定控制提出了挑战。针对变形飞行器当前面临的困难,世界上已有多个国家开展了相关领域的研究计划[4-6],不少高校和科研机构也进行了原型设计和变形机理的研究[7-9]。
滑模变结构方法是一种对不确定参数、扰动具有很强鲁棒性的控制方法,非常适合解决变形飞行器姿态控制这样的强非线性控制问题。文献[10]建立了一种伸缩折叠翼飞行器的LPV模型,并采用自适应滑模控制的方法保证了系统变形过程的稳定性。文献[11]针对一种伸缩翼飞行器,利用输入输出反馈使飞行器的模型精确线性化,并且对于飞行器小翼伸出、收回两个模态设计模糊滑模控制器来保证模态切换的稳定性和平滑性。文献[12]建立了变后掠飞行器的LPV模型,通过线性分数表示法(LFR)得到了等效的线性时变系统,并引入自适应积分滑模控制补偿系统的不确定因素和干扰。这些方法都保证了飞行器在变形过程中的稳定性,取得了良好的控制效果。但是以上方法只针对系统的不确定性和外界干扰设计控制器,没有考虑变形飞行器本身的控制非仿射特性。并且变形飞行器的气动特性较为复杂,也为LPV系统建模带来困难,不利于控制方法的应用。
本文针对一类折叠翼飞行器的控制问题,针对飞行器的控制非仿射特性设计了动态逆控制器,将系统转变为类似仿射的形式。然后基于滑模控制理论设计了滑模控制器来实现对扰动的补偿,并采用动态滑模方法加快收敛速度,抑制抖振。最后,采用数值仿真的方法检验了控制的有效性。
1 变形飞行器模型
1.1 非线性动力学模型
某高速变形飞行器由内部的主体部分和外部的可变机翼部分构成,该变形飞行器的结构图如图1所示。可变机翼部分的外支架绕头部2个支点定轴旋转,从而带动机翼可动桁架结构运动以展开或收拢,从而实现机翼面积和展长的改变。该变形飞行器的两侧机翼对称展开或收拢,定义本文研究的高速变形飞行器的变形量为旋转角ξ,ξ的变化范围为0°~30°。
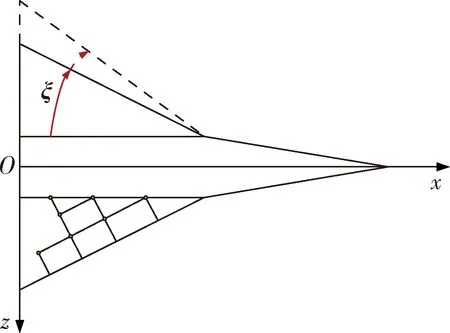
图1 变形飞行器示意图
采用多刚体方法中的牛顿欧拉法对飞行器进行动力学建模,得到该变形飞行器的六自由度非线性动力学模型。为了简化计算方程,假设水平无侧滑,即滚转角φ和侧滑角β满足φ=β=0和角速度p=r=0,将动力学方程进行解耦,得到变形飞行器的纵向非线性动力学模型,以研究变形过程中飞行器的纵向运动。变形飞行器纵向运动方程为
(1)

1.2 气动数据的处理
由于气动专业给出的气动参数是离散的点,为了建立气动参数和旋转角度之间的关系,下面对气动数据进行拟合处理,拟合结果如下所示:
(2)
式中,δe代表飞行器的俯仰舵偏角;ξ为变形翼的旋转角度,单位均为弧度。
2 控制器设计
2.1 动态逆控制器设计
根据气动数据拟合结果可知,舵偏角δe与俯仰力矩系数是多阶非线性的,所以变形飞行器姿态动力学模型是控制非仿射的,即无法把控制量U写成b·δe。为了求解出对应的舵偏角指令,采用动态逆控制的方法将系统转变为仿射非线性模型。
角指令为θr,角速度指令为qr,对跟踪误差作如下坐标变换:

(3)
则姿态角回路可以写成如下二阶不确定系统:
(4)

利用Taylor定理将f(x,u)在u=u0(x)进行级数展开得:
f(x,u)=f0(x)+g(x)u0+Δ(x,u)
(5)
式中:
(6)

(7)

略去高阶项,可以得到u0的表达式:
u0=g-1(x)[f(x)-f0(x)]
(8)
2.2 动态滑模控制器设计
下面采用动态滑模控制的方法对变形飞行器的模型误差进行补偿。取线性滑模面:
s(t)=cx1+x2
(9)
接着构造非奇异终端的动态滑模面:
(10)
式中,设计参数c>0,β>0,ε,γ均为正奇数且满足1<ε/γ<2。
设滑模控制的控制律为v,基于时标分离原理,将系统按照被控量对控制输入量的响应速度分成几个子系统,并假设系统的实际控制量只作用在俯仰角速度回路上,则系统的跟踪误差可以表示为:
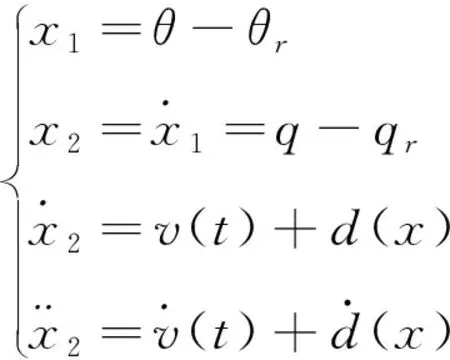
(11)
根据指数趋近律,得到非奇异终端滑模控制律如下:
(cl1+l2+η)sgn(E(t))-kE(t)
(12)
式中,k,η均为设计参数且k,η>0。
下面证明其稳定性:
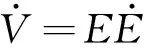
(13)
(14)
根据式(9)可得:
(15)
将式(13)和(10)代入式(15)可得:
(16)
将非奇异终端滑模控制律代入上式可得:

(η+l1+l2)sgn(E(t)}
(17)
式中,E(t)sgn(E(t))=|E(t)|,所以上式变为:
η|E(t)|+cl1|E(t)|-cd(t)E(t)+
(18)

[kE2(t)+η|E(t)|+cl1|E(t)|-
(19)

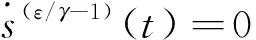

(20)


3 仿真校验
将上文设计的动态滑模控制器和动态逆控制器引入变形飞行器非线性动力学模型中,并对变形飞行器的姿态回路进行仿真研究,以验证所设计的姿态控制器的性能。初始仿真条件为:Ma=7,H=15km,俯仰角指令为每一时刻下的配平俯仰角。
根据俯仰角跟踪曲线和俯仰角速度跟踪曲线可得,本文设计的控制器能够使变形飞行器的飞行姿态在变形过程中在较短的时间内到达期望值,无稳态误差,能够较好地实现姿态指令的跟踪。
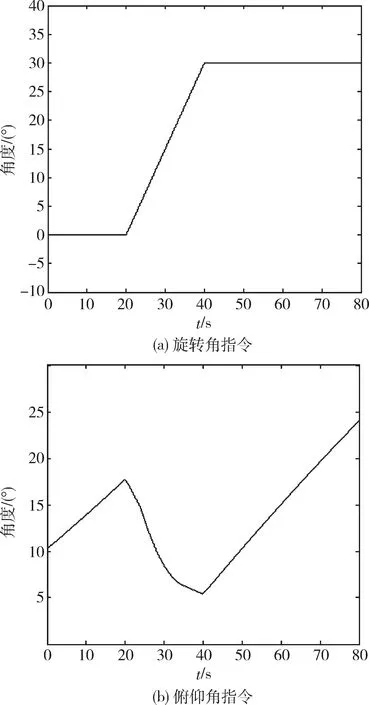
图2 旋转角指令和俯仰角指令

图3 俯仰角跟踪误差曲线

图4 系统响应曲线
4 结 论
针对具有强非线性、不确定性的高速变形飞行器,设计了一种基于动态逆—非奇异终端滑模姿态控制器。首先采用多刚体建模方法建立变形飞行器的纵向非线性动力学模型,并通过拟合工具得到了气动参数随旋转角变化的拟合函数,得到变形飞行器纵向非仿射非线性方程。之后针对性地进行了动态逆控制器设计,将该模型转化为仿射型非线性模型。由于模型的误差会降低动态逆姿态控制精度,本文采用非奇异终端滑模控制对模型误差进行校正。最后,在变形飞行器变形过程中对本文设计的控制器进行仿真验证。仿真结果表明,本文所设计的动态逆—滑模控制器对俯仰角指令具有比较良好的跟踪性能。

