一种引力波探测卫星动态姿态规划方法*

范宇麒 徐 瑞 李朝玉 朱圣英 高 艾 尚海滨 高 越

1. 北京理工大学 深空探测技术研究所，北京 100081 2. 深空自主导航与控制工业与信息化部重点实验室，北京 100081 3. 航天恒星科技有限公司，北京 100086

0 引言

引力波的测量是确认爱因斯坦关于时空和引力以及广义相对论的最广泛认可的方法之一。2016年2月12日，美国LIGO地面引力波探测组宣布首次直接观测到引力波信号，引起了科学家的广泛关注。然而，由于地面实验装置受到低频噪声和有效臂长的限制，只能探测到中高频的引力波信号。要探测低频段的引力波信号，需要在深空环境中搭建空间引力波探测系统。

自20世纪中期以来，空间引力波探测任务如LISA、太极、天琴等正在进行中，这些任务通过构建一个具有长周期稳定的空间类等边三角形系统进行引力波探测，建激光通信链路时，卫星快速姿态机动以实现激光器的长距离对准。

入轨建链、断链后再对准、链路的稳定连接都需要探测器能够进行自主姿态控制。姿态规划是实现多约束下航天器自主姿态控制，并实现激光器长距离自主对准的关键技术之一。众多学者开展了姿态规划可行解搜索方法研究。Frazzoli等提出了一种随机姿态规划算法，用于解决动力学约束和指向约束下的航天器姿态规划问题，其仿真结果表明，该算法在动力学不确定性和环境扰动方面具有较好的鲁棒性[1]。武长青等提出了基于CERRT的多约束抗退绕姿态路径规划，该方法满足指向约束和有界约束，且计算时间短[2]。此外还有基于A*的随机搜索算法[3-5]、几何姿态规划方法[6-9]和势函数法[10-12]等，部分方法已在航天器自主姿态规划方面得到应用。

在引力波大尺度建链的姿态机动过程中，由于卫星的目标姿态与三颗卫星的相对位置有关，故目标姿态随着姿态机动时间的变化而动态变化。针对目标动态变化情况下路径规划问题，机器人领域研究较多，冯林等提出了一种基于对比优化的RRT改进算法，改善了经典RRT算法缺乏稳定性和偏离最优解的问题，并提高了动态环境下路径规划的稳定性，但是算法运行时间较长[13]。刘成菊等针对移动障碍物环境的动态路径规划问题，引入路径缓存区和动态扩展随机树的方法，先进行初始规划再进行重规划，并将算法移植到机器人上，具有良好的效果，但是重规划消耗计算资源过大不适合星上应用[14]。姚远等通过引入相对速度斥力势场和斥力常数模糊控制器对势函数法进行改进，并结合A*算法实现了无人机的动态避障，但未考虑目标点动态移动和无人机姿态[15]。

本文首先对空间引力波探测卫星的大尺度建链任务进行描述，并针对大尺度建链时目标姿态动态变化、姿态约束复杂的问题，将姿态机动规划归纳为一个受终端时刻姿轨耦合约束的多指向规划问题，并根据轨道和姿态机动时间，求解卫星最优目标姿态；然后针对经典RRT算法随机性大和力矩轨迹不平滑的缺点，设计了随机节点启发式扩展方法，在节点违反指向约束时，生成随机节点，并向该随机节点扩展正常数步；接着建立邻近节点深度与目标姿态的函数关系，在每次循环过程更新目标姿态。最后，开展了引力波探测卫星大尺度建链姿态规划仿真，结果表明，本文的姿态规划方法可满足引力波大尺度建链的任务需求，指向偏差相比于经典RRT算法更小，力矩轨迹平滑，能量消耗少。

1 任务描述与问题陈述

1.1 任务描述

由于引力波探测任务中星座的等边三角形臂长为1×106km量级，实现链路构建要求卫星相对姿态对准精度高(1nrad量级)，而基于星敏感器的姿态对准精度仅能达到10μrad量级，因此引力波探测链路构建需要进行如下姿态机动过程[16]：

1) 大尺度建链：根据标称轨道数据计算出参考姿态，3颗卫星借助星敏感器进行大角度姿态机动达到参考姿态；

2) 迭代跟描：扫描星采取适用的扫描策略对被扫描星进行扫描，扫描锥需要覆盖整个不确定锥，扫描过程中，被扫描星保持参考姿态稳定不动；

被扫描星接收到扫描星的激光信号之后进行相应的姿态校正，即进行微角度姿态机动，使激光器指向从光电耦合元件(Charge coupled device, CCD)视场内，并向四象限光电传感器(Quadrant photodiode, QPD)中心靠近，姿态校正完成之后，扫描星可以接收到被扫描星的激光信号;

3) 微角度姿态机动：扫描星接收到被扫描星的激光信号之后，停止扫描并进行微角度姿态机动。至此，扫描星和被扫描星都进行了姿态校正，可实现高精度的对准。

本文主要研究引力波探测任务中的大尺度建链姿态机动自主规划方法，即上述引力波建链步骤中第一步的过程。

引力波探测卫星在姿态机动过程中，目标姿态也在发生变化，若使用目标姿态固定的姿态规划方法，将造成链路构建第一步大尺度建链姿态对准精度10 μrad量级的偏差，而大尺度建链的精度作为卫星执行迭代跟瞄的初始精度，将会延长迭代跟瞄执行的时间，因此必须考虑目标姿态不定和姿轨耦合约束的影响。此外，由于空间明亮天体和卫星内部因素的影响，卫星的大角度姿态机动面临着复杂姿态约束的问题，导致姿态机动的可行空间受到限制，传统的姿态控制方法难以满足当前任务需求。

针对以上讨论的任务需求，提出了引力波探测卫星动态姿态规划方法，通过最优目标姿态求解和改进RRT动态目标姿态规划满足任务需求。

1.2 问题陈述

基于四元数的刚体卫星运动学方程可表示如下：

(1)

式中，q=[q0,q1,q2,q3]T是姿态四元数，表示从本体坐标系到惯性坐标系的旋转，ω=[ω1,ω2,ω3]T表示本体坐标系下的卫星角速度，且

刚体卫星的动力学方程如下：

(2)

式中，J=diag(J1,J2,J3)表示卫星相对于本体系的惯量矩阵，ω×是ω的叉乘矩阵形式，u=[u1,u2,u3]T是卫星本体系下的控制力矩。式(1)和(2)构成了刚体卫星的动力学和运动学模型，由此可以定义卫星的状态变量为：

x=[u1,u2,u3,ω1,ω2,ω3,q0,q1,q2,q3]T

(3)

卫星状态变量是一个10维向量，其中包括力矩3维、角速度3维和四元数4维。该向量可以表示卫星任意时刻的状态，卫星的姿态轨迹即该向量随时间变化的轨迹。

卫星的姿态机动不仅需要满足动力学约束和运动学约束，还需要满足有界约束、指向约束、归一化约束和边界约束。

有界约束：在实际的姿态机动中，执行机构所提供的力矩大小是有限的，因此有力矩有界约束：

ui≤umaxi=1,2,3

(4)

式中，ui为控制力矩分量，umax为控制力矩分量最大值。此外，由于物理结构和角速度量程的限制，卫星本体的角速度也是有限的，故有角速度有界约束：

ωi≤ωmaxi=1,2,3

(5)

式中，ωi为角速度分量，ωmax为角速度分量最大值。

指向约束：引力波探测卫星上安装有成60°夹角的两个激光器，激光器主轴还安装有CCD和QPD等敏感器，为避免明亮天体进入敏感器视场和敏感器指向过于偏离目标指向，主轴指向需满足禁忌约束和强制约束：

(6)

式中，rb为激光器主轴在惯性系下的方向矢量，rs和rv分别为惯性系下的禁忌锥主轴和强制锥主轴，θs和θv分别为惯性系下的禁忌锥半角和强制锥半角。

归一化约束：引力波探测卫星进行大角度姿态机动时，用姿态四元数来描述本体的姿态，其中旋转四元数根据其定义需满足归一化约束，即：

(7)

边界约束：在实际的姿态机动任务中，会给定卫星的初始状态x0和目标状态xf作为姿态规划问题的输入，卫星姿态轨迹的起点和终点必须满足边界约束：

(8)

本节对引力波探测卫星链路构建任务描述后，分析了引力波探测中大尺度建链的任务需求，并将建链中姿态机动问题建模为一个受终端姿轨耦合约束下的多指向姿态规划问题。考虑到原有静态姿态目标时的姿态规划方法难以适用，需设计相应的动态姿态规划方法。

2 建链中目标求解及动态姿态规划

考虑引力波探测卫星目标姿态受姿轨耦合约束的特点，设计了引力波探测卫星最优目标姿态求解方法，并对RRT姿态规划算法进行改进，设计了适用于引力波探测卫星大尺度建链的动态姿态规划算法。

2.1 最优目标姿态求解方法

引力波探测卫星的目标姿态需要根据三颗卫星的实时轨道位置进行解算，而同一时刻轨道位置对应的满足可动激光器摆角有界约束的目标姿态是一个无限集合，因此设计引力波探测卫星最优目标姿态求解方法。

在地心惯性坐标系下，引力波探测卫星编队标称轨道如图1所示，3颗卫星的连线构成等边三角形。图2是卫星最优目标姿态示意图，其中，SC表示引力波探测卫星，SC1、SC2和SC3共同构成卫星编队，rb1为SC1指向SC2的方向矢量，rb2为SC1指向SC3的方向矢量，r1和r2为SC1两个激光器的方向矢量。

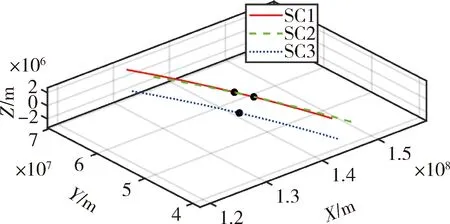
图1 引力波探测卫星编队标称轨道

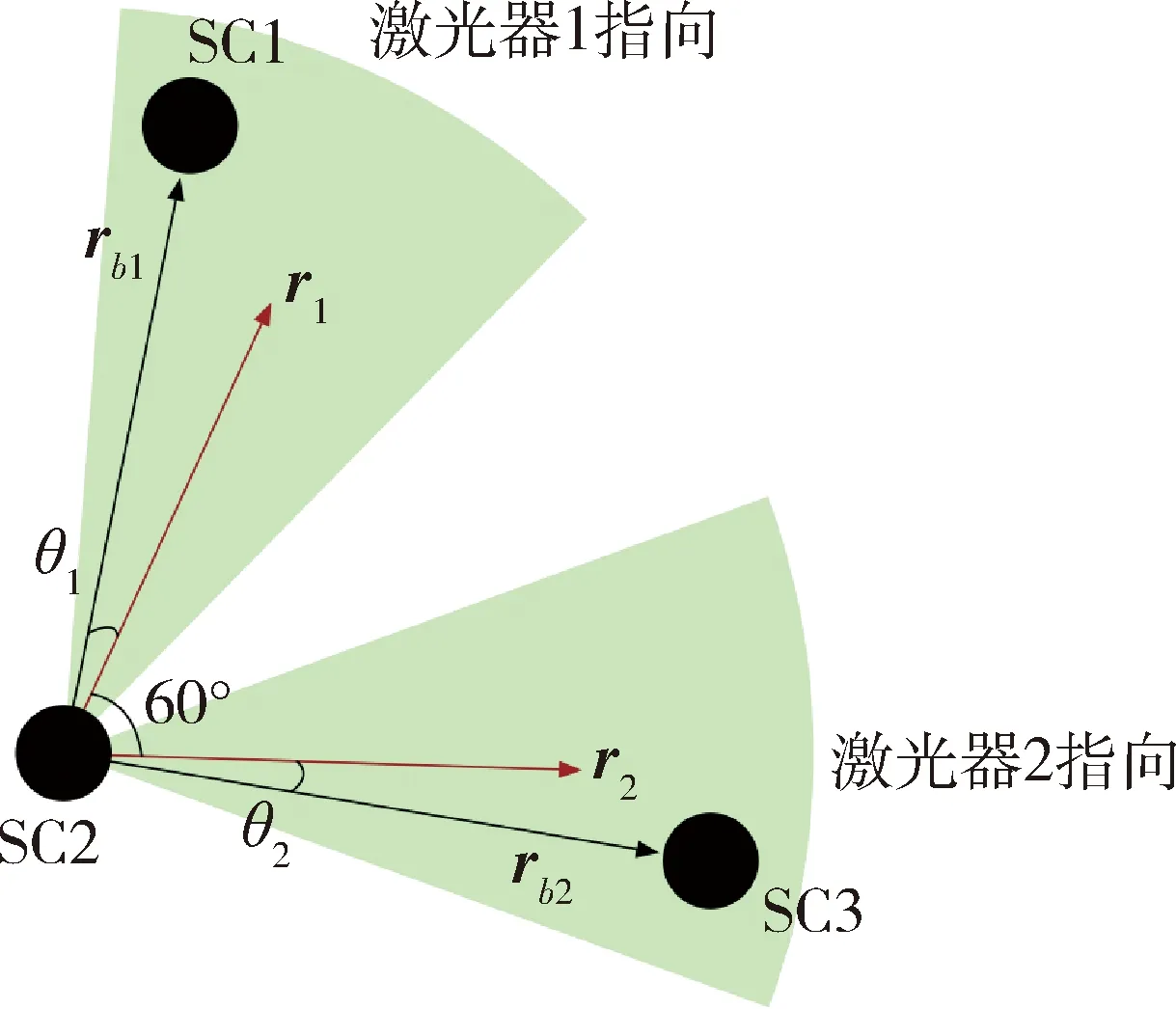
图2 目标姿态示意图

根据轨道计算得到的rb1和rb2的夹角在59°-61°之间浮动，如图3所示。由于卫星上两个激光器安装构型为固定60°夹角，且在姿态机动的过程中不考虑激光器的机动能力，故SC1的目标姿态应该保证激光器指向尽量靠近对应的卫星链路指向，即r1尽量靠近rb1，r2尽量靠近rb2。因此，SC1的目标姿态无法通过解析计算求得，需要在终端时刻，求解一个最小二乘问题，得到卫星的目标姿态四元数。该最小二乘问题可表示为：

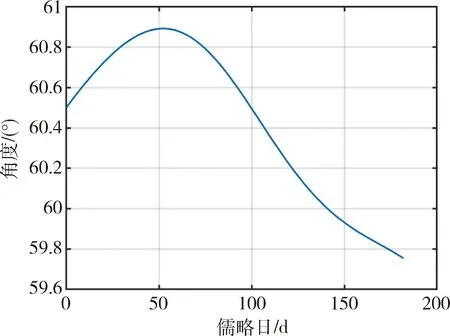
图3 rb1和rb2的夹角变化

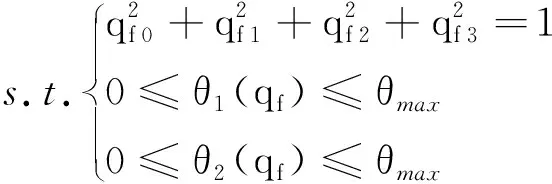
(9)

式中，θ1为r1和rb1的夹角，θ2为r2和rb2的夹角，θ1和θ2是目标姿态四元数qf=[qf 0,qf 1,qf 2,qf 3]T的函数，θ1和θ2被称为呼吸角，θmax为激光器摆角控制机构可摆动的最大角度。该问题的最优解为卫星的目标姿态四元数。可在三颗星标称轨道上选择均匀分布的关键节点，求其对应的目标姿态，并对关键节点的目标姿态进行插值，计算任意时刻目标姿态。

将上述求解最小二乘问题的过程表示成一个函数f，目标姿态必须满足终端时刻姿轨耦合约束，并且是姿态机动时间的函数：

qf=f(tf)

(10)

2.2 基于改进RRT的动态目标姿态规划算法

目前用于姿态规划的方法主要有势函数法、随机规划方法、几何方法等，性能对比如表1所示，可以看出随机规划方法处理复杂约束能力强、可进行多星规划，并且对指向约束的处理能力较强。因此，本文对RRT算法进行改进，设计了随机节点启发式扩展方法和目标姿态实时更新方法，实现力矩轨迹平滑和目标姿态动态跟踪。

表1 姿态规划方法对比

RRT算法是基于采样的快速搜索随机算法，在1998年由LaValle等提出[17]，并被广泛应用于机器人的运动规划中。

然而，经典的RRT算法有以下缺点和不足：

1)具有较大的随机性；

2)生成路径不平滑；

3)只适用于静态环境。

针对以上问题，对RRT算法主要提出以下2点改进。

1)随机节点启发式扩展方法

为了实现姿态轨迹平滑，减少算法的不确定性，引入目标节点和指向约束区域作为随机节点扩展启发式信息，区别于经典RRT算法在整个状态空间中无差别生成随机节点，仅在节点违反指向约束时向随机节点扩展，且随机节点满足指向约束并位于当前节点的邻域内，其他情况则向目标节点扩展。如图4所示，随机扩展树从初始节点向目标节点扩展，若当前节点xcollided违反指向约束，在当前节点邻域内生成一个满足指向约束的随机节点xrandom，在随机树上找到距该随机节点最近的节点并标记为分支节点xbranch，从分支节点向随机节点扩展m步，m为大于等于1的整数，m越大，力矩轨迹越平滑；但是m不能过大，否则路径将偏离向目标节点靠近的趋势，并消耗更多的燃料。

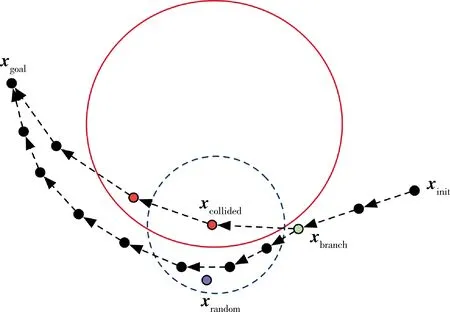
图4 随机节点启发式扩展示意图

在完成随机节点启发式扩展之后，随机扩展树中将包含为满足指向约束而产生的分支，在接下来的随机树扩展过程中，随机树将沿着新产生的分支向目标节点扩展。应用随机节点启发式扩展方法使随机树只在指向约束区域附近产生分支，有效减少了随机树的分支节点，从而使力矩轨迹更加平滑。

2)目标姿态实时更新方法

在目标点动态变化的环境下，基于RRT的姿态规划方法需要作适当的改进，才能保证终端时刻姿轨耦合约束的满足。为了减小计算资源消耗并实现目标姿态不定的动态规划，在算法每次循环过程中，计算邻近节点的深度，即路径所包含的节点数。引入最优目标姿态求解方法，并根据邻近节点深度实时更新目标姿态，从而对目标节点姿轨耦合约束进行满足。目标姿态和邻近节点的深度的关系可表示如下：

式中，ΔT为相邻两节点之间的时间间隔，N为邻近节点的深度，f为最优目标姿态求解方法对应的函数映射，将姿态机动时间tf映射为最优目标姿态。

综合随机节点启发式扩展方法和目标姿态实时更新方法，得到基于改进RRT的动态目标姿态规划算法流程图如下：

图5 基于改进RRT的动态目标姿态规划算法流程图

在扩展节点时，两相邻节点必须满足动力学约束和运动学约束：由式(1)和(2)并运用一阶欧拉法将其离散化，可得出卫星的动力学约束和运动学约束方程：

(11)

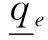
(12)

ρ=(Cq)TR1(Cq)+ωTR2ω

(13)

3 仿真校验

引力波探测卫星需要进行大角度姿态机动，将初始时刻姿态转向最优目标姿态。设初始时刻为t0，进行任意初始时刻的大尺度建链仿真。仿真输入仅需要卫星编队标称轨道和初始状态，分别用改进RRT算法和经典RRT算法进行姿态规划，仿真参数如表2所示，考虑3个禁忌约束和1个强制约束，卫星在z轴和[0,0.8660,0.5000]T方向分别安装了一个激光器。本文仿真使用相同的运行环境：Mac OS12.1系统，计算机主频1.4GHz，内存8GB。

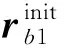
表2 仿真条件

图6为改进RRT算法规划的引力波探测卫星激光器的指向路径和收敛轨迹，图6(a)中上三角为禁忌锥的边界，下三角为强制锥的边界，图6 (b)中红色曲面为禁忌锥在姿态球上的投影，绿色曲面为强制锥在姿态球的投影，图6(c)中实线表示指向1的当前指向与目标指向间的夹角，虚线表示指向2的当前指向与目标指向间的夹角。可见激光器从初始指向收敛到目标指向，并且指向路径满足禁忌约束和强制约束。

图6 改进RRT算法姿态规划结果

图7为引力波探测卫星三轴力矩轨迹对比图，其中图7 (a)为改进RRT三轴力矩轨迹，图7 (b)为传统RRT三轴力矩轨迹，可见改进RRT算法相比于经典RRT算法力矩轨迹较为平滑且突变较少，符合实际。

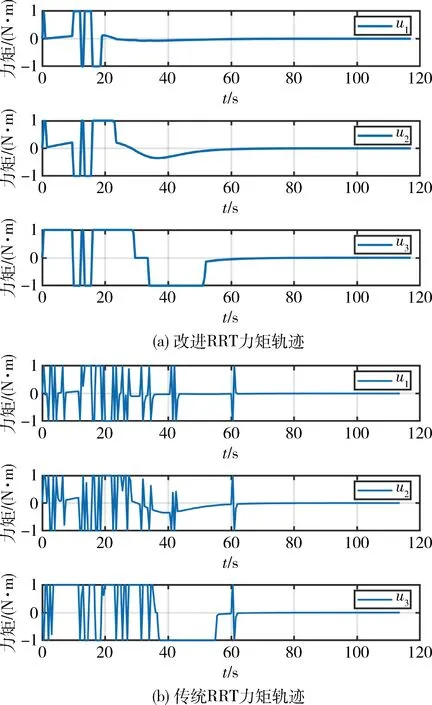
图7 力矩轨迹对比

对上述任务场景，分别用经典RRT算法和改进RRT算法进行5次姿态规划，对比其性能指标，总结如表3所示：

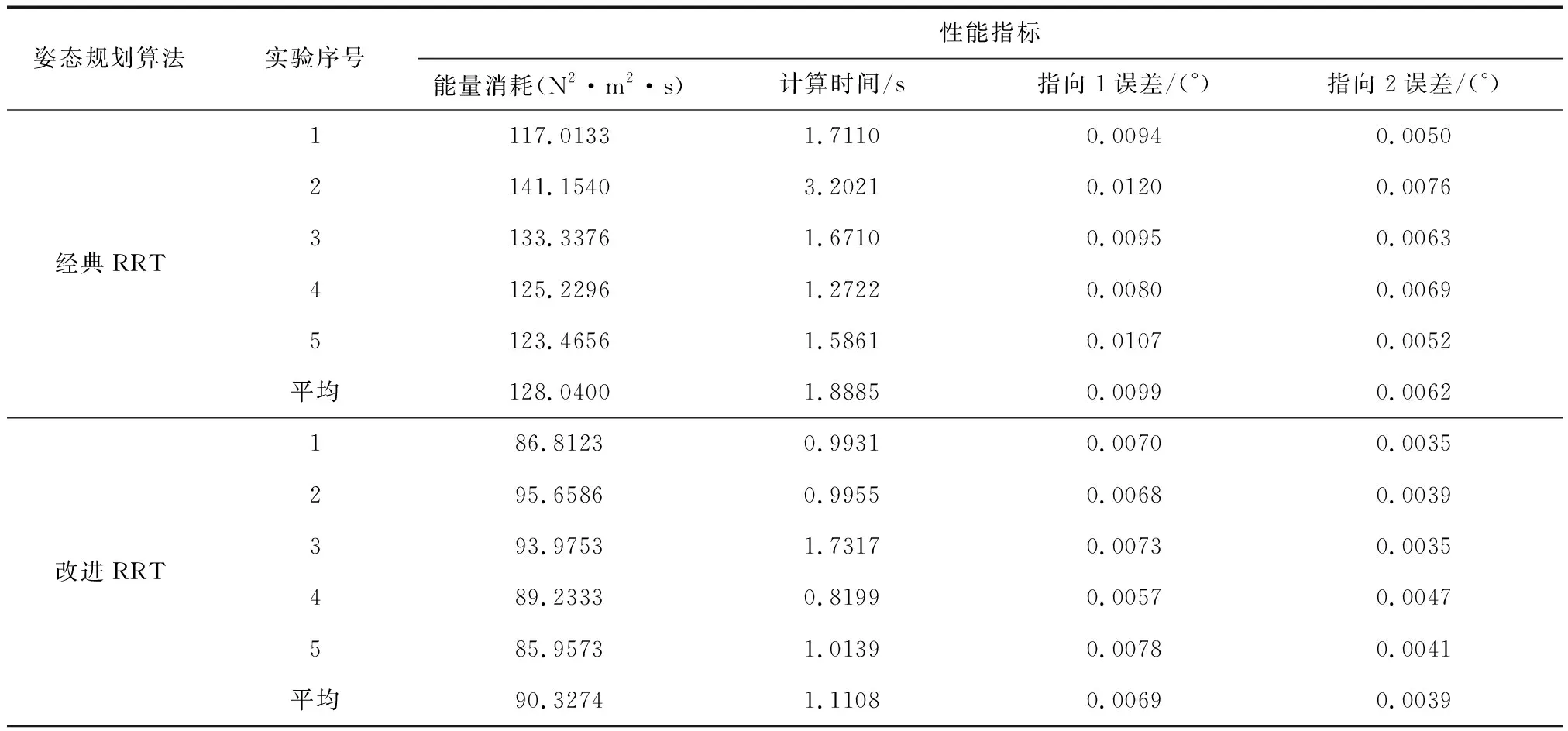
表3 经典RRT和改进RRT性能指标对比

其中，终端时刻指向误差考虑了在姿态机动的过程中3颗星位置时变带来的指向误差，从表中可以看出改进RRT算法在平均能量消耗和平均计算时间方面均优于经典RRT算法，并且终端时刻指向1误差降低了30.3%，指向2误差降低了37.1%，这将显著减小后续迭代跟瞄的时间。

4 结论

介绍了空间引力波探测任务的背景，研究了引力波探测卫星大尺度建链的动态姿态规划方法，完成了以下工作：

1)根据三颗卫星的运行轨道，通过求解最小二乘问题，求解引力波探测卫星在任一时刻的姿态机动目标姿态；

2)基于RRT姿态规划算法，设计了随机节点启发式扩展方法和目标姿态实时更新方法，实现了力矩轨迹平滑和目标动态跟踪。

本文将引力波探测卫星作为单个刚体进行建模，并未考虑激光器的可动能力，接下来仍需对复杂约束下、带有多可动部件的卫星姿态规划方法展开进一步的研究。