基于傅里叶级数的椭圆球面波信号时频分析

赵乐源，刘传辉，刘锡国，张 磊

（1.海军航空大学，山东 烟台 264001；2.山东省信号与信息处理重点实验室，山东 烟台 264001；3.中国人民解放军92853 部队，辽宁 葫芦岛 125000）

0 引 言

基于椭圆球面波（Prolate Spheroidal Wave Functions，PSWFs）信号的非正弦通信是近些年来提出的一种新型通信方式，其采用时域正交、频域混叠的PSWFs 信号作为载波，突破了利用正余弦波信号进行信息传输的传统思维。得益于PSWFs 信号具有双完备正交性、时域波形奇偶对称性、高时频能量聚集性、时间带宽积与频谱灵活可控等优良特性，基于PSWFs 信号的非正弦通信可直接在时频域进行信号波形设计，具有信号波形设计灵活、高频谱效率等诸多优势，是一种极具应用前景的通信新体制。

时频特性作为PSWFs 信号的基础性质之一，在基于PSWFs 信号的非正弦通信特别是时频检测中具有如下潜在应用价值。传统的PSWFs 调制信号的检测大都采用基于正交性的相关检测，在信道条件较好的情况下，检测效果较好；而在信道条件较差正交性被破坏的情况下，检测效果较差。基于PSWFs 信号的时频检测是根据PSWFs 信号的时频特性，从时频域中提取特征参量，如时频峰值点、时频中心点等，用以信号的检测。此类方法根据PSWFs 信号的自身特性，有望实现检测效果的提升。

PSWFs 信号时频特性是时频检测的基础。为进一步研究PSWFs 信号的时频特性，文献[9]采用Wigner-Ville分布（Wigner-Ville Distribution，WVD）分析了PSWFs信号WVD 交叉项的时频特性。文献[10]采用平滑Wigner-Ville 分布（Smoothed Wigner-Ville Distribution，SWVD）分析了交叉项抑制情况下的PSWFs 信号时频特性。文献[11]采用短时傅里叶变换（Short Time Fourier Transform，STFT）和S 变换（Stockwell Transform，ST）分析了线性时频方法下的PSWFs 信号时频特性。研究发现，WVD 时频分辨率高，能够获取PSWFs 信号时频域中更为精确的特征参量，对于PSWFs 信号时频检测具有重要意义。

然而，PSWFs 信号无闭式解析解，当前通常采用数值求解的方式产生，故对于PSWFs 信号时频特性的研究是通过大量数值仿真实验得来的。通过数值仿真得到的PSWFs 信号时频特性，由于无显式表达式，特别是PSWFs 信号某一频率随时间变化表达式，导致其时频特性难以应用于PSWFs 信号时频检测。

针对上述问题，本文引入傅里叶级数，将PSWFs 信号按傅里叶级数展开，分析PSWFs 信号每一频率随时间的变化情况，同时结合数值仿真，重点研究PSWFs 信号WVD 时频中心点、时频峰值点、时频零点等特殊点随自身参数（时间带宽积、阶数）之间的变化规律。

1 PSWFs 信号基本原理

PSWFs 信号定义和性质是其应用的基础。下面简要梳理PSWFs 信号的定义和奇偶对称性，为PSWFs 信号傅里叶级数展开可行性及时频分析奠定理论基础。

文献[1]定义的PSWFs 信号φ(,)由积分方程给出，PSWFs 信号积分方程表达式为：

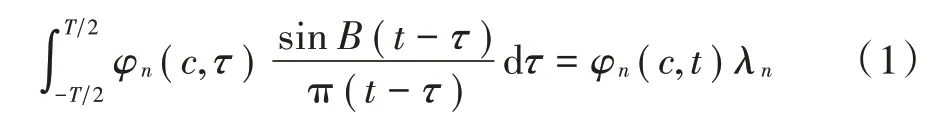
PSWFs 信号具有奇偶对称性，其对称性与阶数相关，满足：

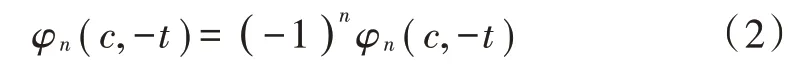
2 基于傅里叶级数的PSWFs 信号时频特性分析

文献[12]指出，任意波形总能进行谱分解，分解为不同频率、不同振幅的简谐波的线性叠加。PSWFs 信号作为一类非正弦非平稳信号，虽无闭式解析表达式，但可以由傅里叶级数进行表征。下面首先分析PSWFs 信号的傅里叶级数展开式，然后将PSWFs 信号傅里叶级数展开式与WVD 相结合，分析PSWFs 信号频率随时间的变化情况。

2.1 基于傅里叶级数的PSWFs 信号WVD 展开

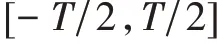
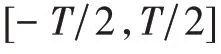
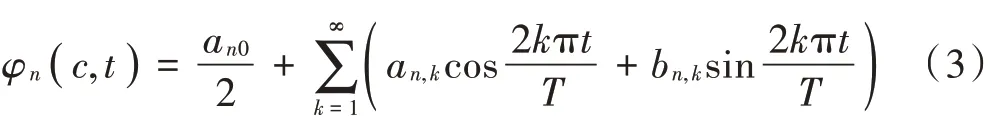
式中：

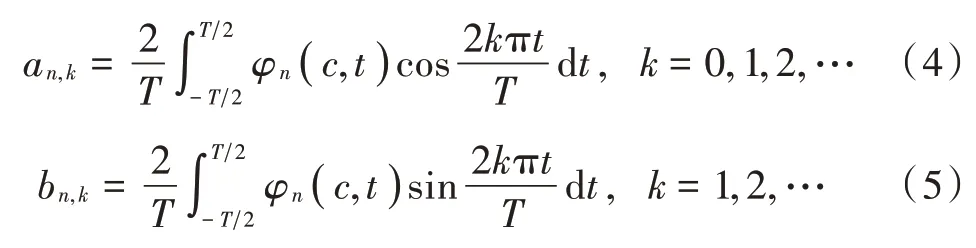
PS WFs 信号具有奇偶对称性，故可对式（3）作进一步简化，偶数阶PSWFs 信号(,)和奇数阶PSWFs 信号(,)可分别表示为：

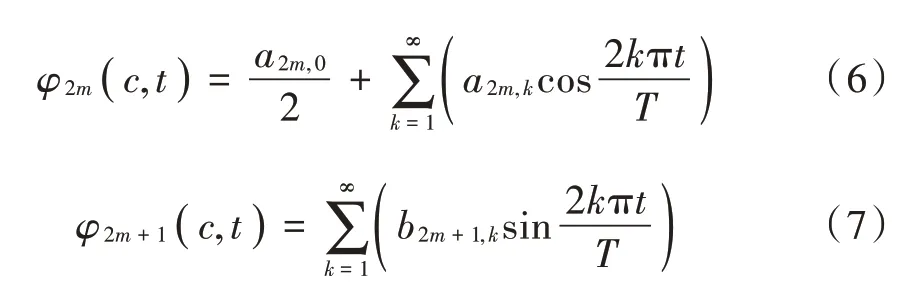
与一般信号一致，根据文献[13]，PSWFs 信号WVD可表示为：

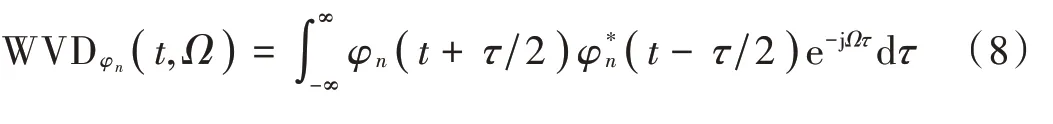
将式（6）代入式（8），并化简得偶数阶PSWFs 信号WVD(,)表示为：

将式（7）代入到式（8），并化简得奇数阶PSWFs 信号WVD(),表示为：

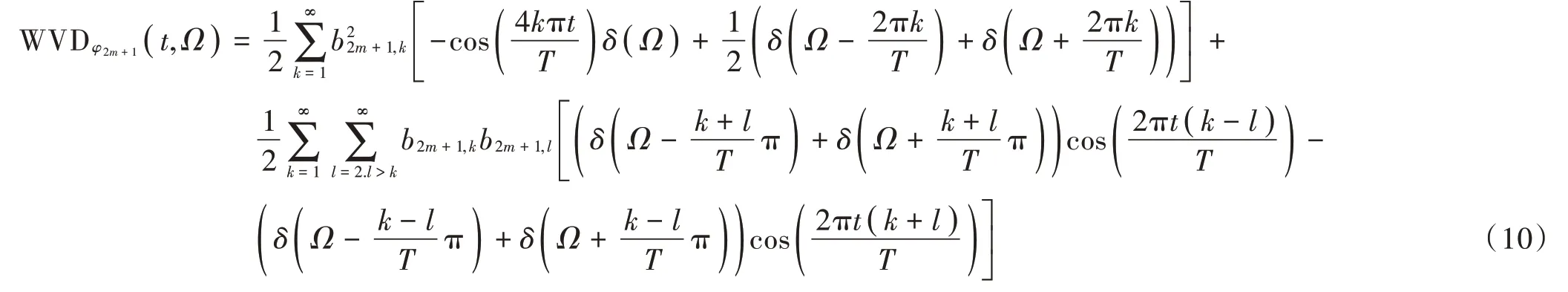
通过式（9）、式（10），即可分析PSWFs 信号某一特定频率幅值随时间的变化情况。

2.2 特性分析

下面结合PSWFs 信号基本原理及2.1 节分析，对PSWFs 信号WVD 对称性、时频中心点进行研究。

特性1：PSWFs 信号WVD 关于时间轴对称、频率轴对称，且关于=0，=0 中心对称。

证明：

由式（2）、式（8）可得：

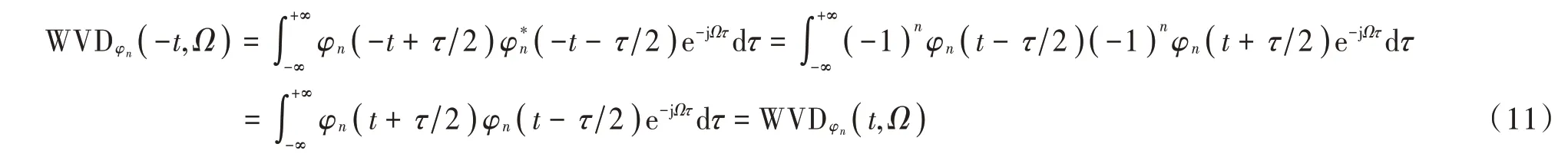
由式（11）可知，PSWFs 信号WVD 关于时间轴对称。

此外，由式（2）、式（8）可得：

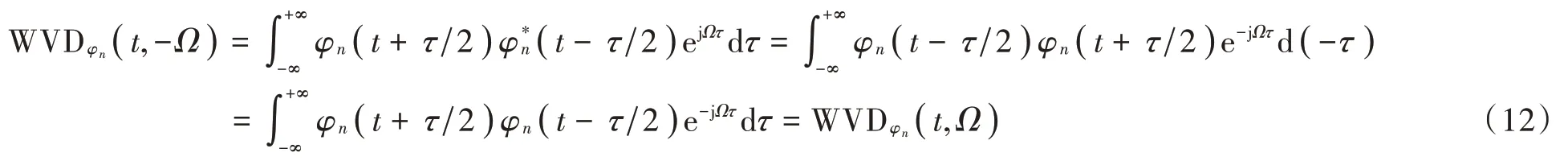
由式（12）可知，PSWFs 信号WVD 关于频率轴对称。

另外，结合式（11）、式（12）可得：

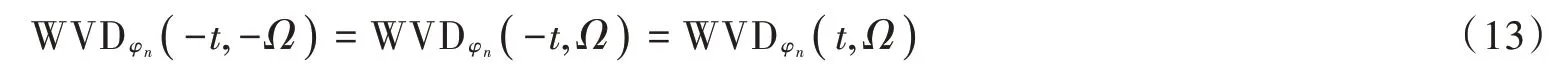
由式（13）可知，PSWFs 信号WVD 关于=0，=0 中心对称。

证毕。

特性2：PSWFs 信号WVD 时频中心点幅值极性与PSWFs 信号阶数有关。阶数为偶数时，PSWFs 信号WVD时频中心点幅值极性为正；阶数为奇数时，PSWFs 信号WVD 时频中心点幅值极性为负。

证明：

令=0，即在0 频率处，式（9）可简化为：

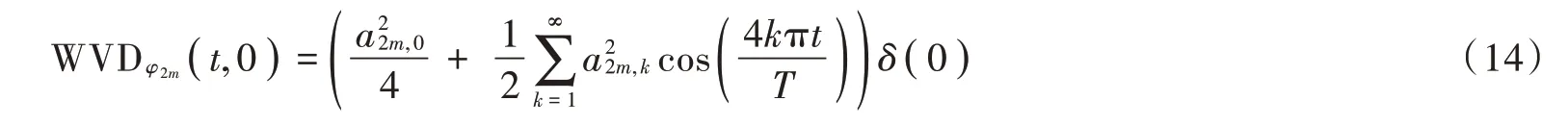
式（14）表明，在0 频率处，偶数阶PSWFs 信号时间分布为余弦信号的叠加。

令=0，即在0 时间处，式（9）可简化为：

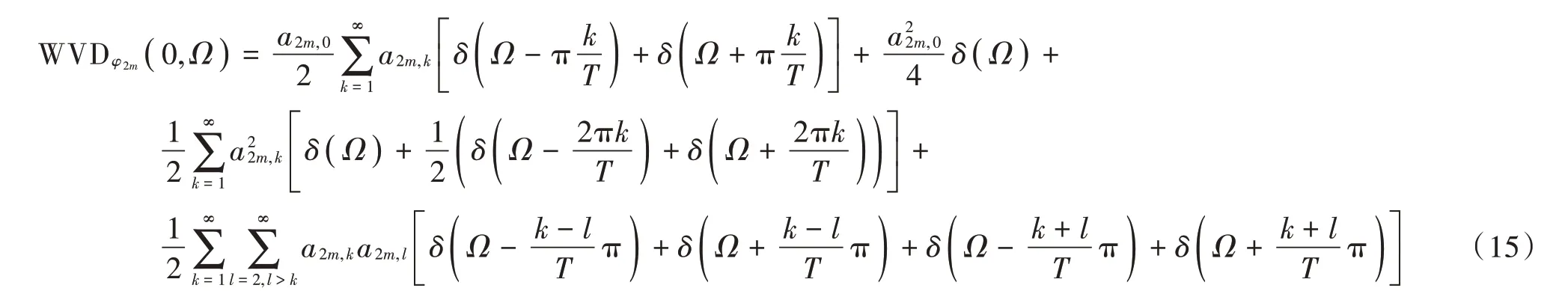
式（15）表明，在0 时间处，偶数阶PSWFs 信号频率分布为各频率处冲激函数的叠加。

令式（9）中，=0，=0，则偶数阶PSWFs 信号WVD 在时频中心为：

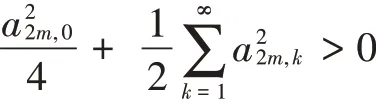
令=0，即在0 频率处，式（10）可简化为：

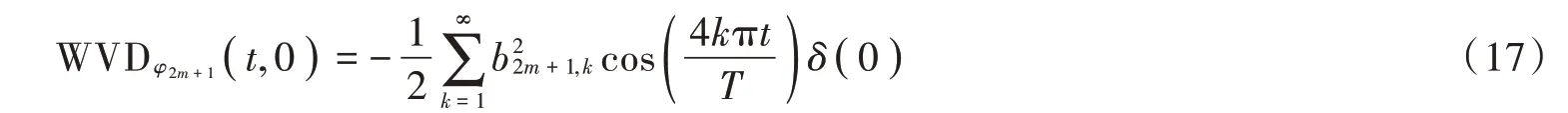
式（17）表明，在0 频率处，奇数阶PSWFs 信号时间分布为余弦信号的叠加。

令=0，即在0 时间处，式（10）可简化为：

式（18）表明，在0 时间处，奇数阶PSWFs 信号频率分布为冲激函数的叠加。令式（10）中，=0，=0，则奇数阶PSWFs 信号WVD 在时频中心为：

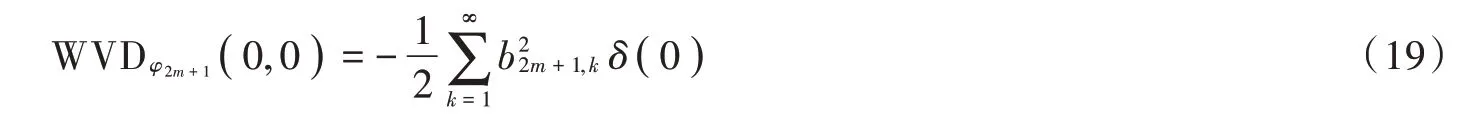
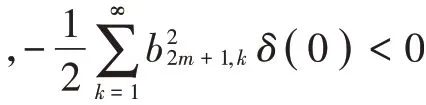
证毕。

3 数值仿真

基于傅里叶级数的PSWFs 信号WVD，可分析PSWFs 信号某一频率随时间变化情况。但PSWFs 信号无闭式解析解，无法通过显式表达式完全分析其时频特性。下面结合数值仿真，验证理论分析的正确性；同时，进一步利用数值仿真探索基于WVD 的PSWFs 信号时频特性。

为便于总结特性规律，下面引入时频峰值点(,)概念，时频峰值点(,)对应的幅值 |(,)|满足：

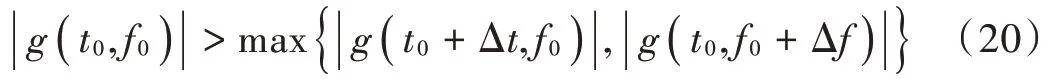
式中，(+Δ,+Δ)为PSWFs 信号时频峰值点(,)邻域，时频峰值点示意图如图1 中点所示。

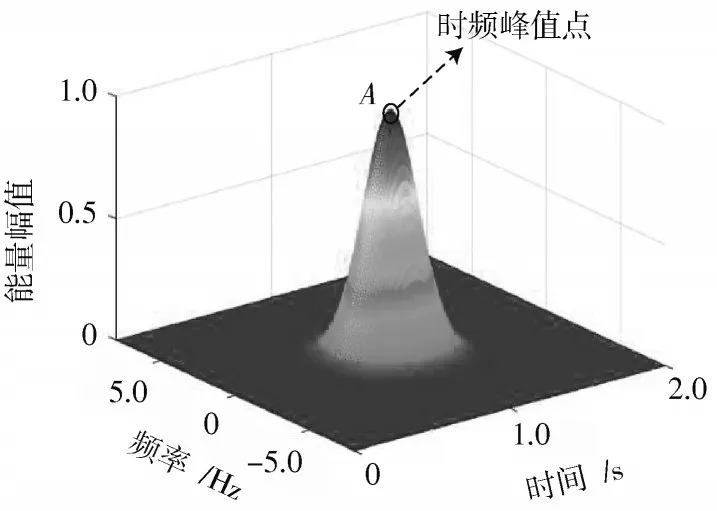
图1 时频峰值点示意图

系统参数设置如表1所示。

表1 系统参数设置

3.1 PSWFs 信 号WVD 情 况

图2 给出了时间带宽积为4 Hz·s 的0～3 阶PSWFs信号WVD，将时间区间移到了[0，2 s]。

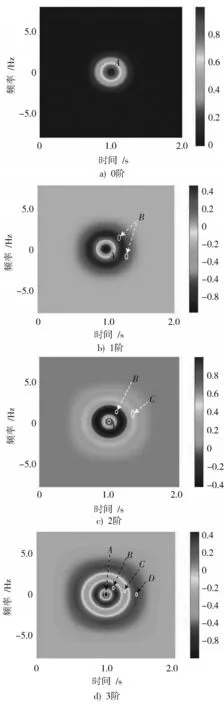
图2 PSWFs 信号WVD

由数值仿真结果可知：

1）PSWFs 信 号WVD 关 于 时 间 轴=1.0 s 对 称，关于频率轴=0 对称，且关于（1.0 s，0）中心对称，与理论分析一致。

2）0 阶PSWFs 信号与2 阶PSWFs 信 号 在WVD 时频中心（1.0 s，0）幅值为正，1 阶PSWFs 信号与3 阶PSWFs信号在WVD 时频中心（1.0 s，0）幅值为负，与理论分析一致。

3）0～3 阶PSWFs 信号在WVD 时频中心（1.0 s，0）都含有一个时频峰值点，如图2a）～图2d）中点所示。但随着阶数增加，PSWFs 信号峰值点数量增加，如1 阶PSWFs 信号除在WVD 时频中心有一个峰值点外，在时频中心外环也含有时频峰值点，如图2b）中处所示。并且，时频峰值点连线组成时频峰值圈。

4）若将PSWFs 信号WVD 时频峰值点也看作一个特殊的峰值圈，则PSWFs 信号WVD 时频峰值圈数量与PSWFs 信号阶数有关，满足=+1。如2 阶PSWFs信号，含有3 个时频峰值圈（或点），如图2c）中，，所示；3 阶PSWFs 信号，含有4 个时频峰值圈（或点），如图2d）中，，，所示。

3.2 PSWFs 信号频率幅值随时间变化情况

由3.1 节分析可知，0 频率作为PSWFs 信号的中心频率，对于时频提取具有重要参考意义。下面结合基于傅 里 叶 级 数 的PSWFs 信 号WVD 展 开，对5 阶、6 阶PSWFs 信号0 频率幅值随时间变化情况展开分析。考虑到PSWFs 信号无显式表达式，难以通过显式表达式分析PSWFs 信号0 频率幅值随时间带宽积、阶数变化情况，下面结合数值仿真进行分析。

图3 给出了在不同时间带宽积下，第5 阶、第6 阶PSWFs 信号0 频率幅值随时间变化情况。

图3 PSWFs 信号0 频率幅值随时间变化情况

由数值仿真结果可知：

1）PSWFs信号0频率幅值随时间非平稳变化，第5阶PSWFs 信号含有6 个极大值点，5 个极小值点，10 个过零点；第6 阶PSWFs 信号含有7 个极大值点，6 个极小值点，12 个过零点。结合其他阶PSWFs 信号情况，第阶PSWFs 信号0 频率幅值随时间变化，在给定时长内，含有+1 个极大值点，个极小值点，2个过零点。

2）由时间区间中心向时间区间两端，各个极点幅值的绝对值逐渐减小。

3）对于第个极值点t，随着时间带宽积逐渐增大，极值点t的位置逐渐向时间中心=1.0 s 移动。而极值点含有信号较大的能量，故随着时间带宽积的增大，0 频率处信号能量逐渐向时间中心聚集。

4 结 语

针对数值仿真无法给出PSWFs 信号某一频率随时间变化显式表达式的问题，本文引入傅里叶级数，将PSWFs 信号按傅里叶级数展开，利用WVD 分析每一频率随时间变化情况，并重点研究了PSWFs 信号WVD 时频中心点、时频峰值点、时频零点等特殊点随自身参数（时间带宽积、阶数）之间的变化规律。相关结论及方法可为PSWFs 信号时频检测提供重要理论参考价值，如时频中心点、0 频率处幅值随时间变化情况，可作为重要特征参量用于时频检测，这也是下一步研究的方向。