基于小波函数的模糊大脑情感学习分类器

高佳倩，潘培华，孙 园，王绮楠，郭前进

(厦门理工学院电气工程与自动化学院，福建 厦门361024)

分类问题是机器学习、模式识别与数据挖掘等领域内重要的研究内容，目前有大量的算法运用于分类研究，包括决策树(decision tree)、朴素贝叶斯(naïve bayes，NB)、人工神经网络(artificial neural network，ANN)、K-近邻(k-nearest neighbor,KNN)、支持向量机(support vector machines，SVM)等[1-2]。在众多算法中，由于神经网络拥有自学习和良好的泛化能力，因此被广泛地应用于分类问题。小脑神经网络(cerebellar model articulation controller neural network，CMACNN)和大脑情感学习神经网络(brain emotional learning neural network，BELNN)是人工神经网络中2种成熟的神经网络模型，且已有文献成功地将2种神经网络应用于分类问题[3-4]。为提高模型的性能，一些学者尝试对网络进行改进，例如将模糊系统加入小脑神经网络和大脑情感学习神经网络得到模糊小脑模型(fuzzy cerebellar model articulation controller，FCMAC)和模糊大脑情感学习模型(fuzzy brain emotional learning，FBEL)，以对不确定的输入信号进行处理，降低输入信号的复杂性[5-6]。但当输入信号为含有噪声的复杂数据时，传统的模型函数缺少对噪声的处理能力，影响FBEL模型对复杂数据的处理能力。为此，本文提出一种小波模糊大脑情感学习分类器(wavelet fuzzy brain emotional learning classifier，WFBELC)，用小波函数替换原本的高斯函数作为隶属函数，改进FBEL对复杂数据的处理能力，从而提高算法精度和分类效果。

1 WFBELC的基本结构

小波模糊大脑情感学习分类器(WFBELC)共分为5部分:感觉输入、感觉皮层、权值空间、杏仁核、眶额皮质的加权求和空间和输出空间。

小波模糊大脑情感学习分类器的基本结构如图1所示。

图1 小波模糊大脑情感学习分类器的基本结构Fig.1 Structure of wavelet fuzzy brain emotional learning classifier

第1部分是感觉输入层。输入向量I=[I1,…,Ii,…,In]T∈Rn，Ii代表第i个输入样本。

第2部分是感觉皮层空间。感觉输入在该空间进行模糊化处理。

如果I1为B1且I2为B2，…，且In为Bn，则：

(1)

如果I1为B1，且I2为B2，…，且In为Bn，则：

(2)

式(1)和(2)为杏仁核和眶额皮质的模糊推理规则。其中，i=1,2,…,n，n为输入样本数；j=1,2,…,m，m为神经元个数；Bi为第i个输入Ii对应的输入模糊语言值；A为杏仁核的输出；O为眶额皮质的输出；Vij、Wij分别表示杏仁核和眶额皮层权重。Ath表示丘脑信号，Vth表示Ath传输到杏仁核时的连接权值。

由于小波函数相比于高斯函数有时频局部化特性[7-8]，对突变信号的感知更灵敏，且能消除噪声。因此，采用小波函数进行模糊化，模糊化公式[9]为

(3)

式(3)中：Sij代表式(1)中第i个输入Ii对应的输入模糊语言值Bi；mij和σij为小波函数的平移参数和伸缩参数；Ii代表第i个输入样本。

第3部分是权值空间。从感觉皮层到杏仁核，每个节点都有一个对应的连接权值V，V=[V111,…,Vijt,…,Vnmk]T∈Rnmk；到眶额皮质系统，每个节点对应的连接权值为W，W=[W111,…,Wijt,…,Wnmk]T∈Rnmk。权值V和W中的t=1,2,…,k，k代表分类样本的类别维度，若分类数据集是多分类时k≥3。此外，丘脑接收的最大输入信号直接输入到杏仁核，被称为丘脑信号Ath，表示为

Ath=max(Sij)。

(4)

第4部分是杏仁核、眶额皮质的加权求和空间。眶额皮质节点接收到的信号主要是来自感知层的刺激信号Sij。因此，眶额皮质的输出O表示为

(5)

杏仁核接受来自感知层的刺激信号Sij和丘脑信号Ath，且丘脑信号经过丘脑权值Vth，则杏仁核的输出A表示为

(6)

第5部分是输出空间。u是小波模糊大脑情感学习分类器的输出，表示为

u=A-O。

(7)

输出结果u为具体数值，而分类器的输出应反映类别标签，因此需要将数值转化为与实际类别相同的标签值。通常采用sigmoid函数将结果映射到[0,1]之间，公式为

(8)

对于二分类问题，设置一个[0,1]之间的值为阈值，y若大于阈值置为1，小于阈值置为0，以此对应2种类别。而对于多分类问题，该方法可能会产生一些障碍。因此，通过改变分类器的类别输出形式，采用最大置1法[10]，使模型预测结果与标签值对应。举例说明：一个数据集样本分为3类，用[1,0,0]表示第1类，[0,1,0]表示第2类，[0,0,1]表示第3类。令分类器输出结果u为1×3的矩阵，即u=[u1,u2,u3]，通过sigmoid函数得到y=[y1,y2,y3]，再找出y1,y2,y3中的最大值并将其置1，其余的结果置0，如下式(9)所示:

(9)

经过置1法后的输出值y与样本实际类别的表示形式相同，且认定其与对应类别的相似度最高。

2 WFBELC的参数自学习规则

小波模糊大脑情感学习分类器(WFBELC)中杏仁核和眶额皮质情感学习过程都是一个动态的权重调节过程，这两部分主要是对杏仁核权值V和眶额皮质权值W进行学习更新，更新公式[11]为

ΔVij=λv(Sijmax(0,REW-A))。

(10)

ΔWij=λw(Sij(A-O-AthVth-REW))。

(11)

式(10)和(11)中：λv和λw分别为更新权值V和W的学习速率，是影响学习速度的关键因素。REW是情感刺激或强化刺激的奖励信号，促进杏仁核学习过程的进行，具体表示为

REW=k1e+k2y。

(12)

式(12)中：输出误差e=T-y，T为样本的标签值，y为分类器输出的预测值；k1和k2均为信号常数增益。小波函数中平移参数mij和伸缩参数σij的更新采用梯度下降法，更新公式为

(13)

(14)

(15)

(16)

3 仿真验证

实验仿真环境如下：处理器采用Intel i5-1035G1，基准频率1 GHz，加速频率3.6 GHz；RAM内存16.0 GB；操作系统为Windows10，64位操作系统，基于x64的处理器；编程环境为Matlab R2019a。选取加州大学欧文分校机器学习资源库[12]中的3个分类数据集，对所提出WFBELC的性能进行验证。

3.1 数据集介绍

仿真实验采用的3个数据集分别是Wine、Sonar和Ionosphere数据集。表1列出数据集的基本信息及数据集的划分情况。仿真时，将数据集按照7∶3的比例划分训练集和测试集。如表1所示，Wine数据集包含178个样本，13种特征，为3分类样本；仿真时训练集有125个样本，测试集有53个样本。同理，可知Sonar和Ionosphere数据集的信息。

表1 数据集基本信息及划分情况Table 1 Dataset information and classification 单位：个

3.2 仿真参数设置

为加快训练收敛速度，在建立仿真模型前须对数据集参数进行归一化。本文采用的归一化方式是离差标准化，对原始数据进行线性变换使结果落到[0,1]区间，公式为

(17)

式(17)中：x是原始数据；x*是归一化后的数据；min、max分别是样本数据中的最小值和最大值。

表2为不同数据集对应的仿真参数设置。

表2 不同数据集的仿真参数设置Table 2 Parameters for simulation in different datasets

小波函数的平移参数mij和伸缩参数σij初始值均设为随机值，权值V和W设为0。通过参数自学习规则和梯度下降法对参数mij、σij、V、W进行更新，更新时对应的学习率λm、λσ、λv、λw设置相等。

3.3 仿真性能评价指标及结果分析

3.3.1 性能评价指标及收敛性分析

为评估分类器的性能，以测试样本的分类准确率为评价指标，即为

(18)

式(18)中：Acc表示测试准确率；T为正确预测的样本个数；S为测试样本总数。为确保公平比较，每个数据集在不同算法模型上均进行10次仿真，且在每次仿真前会打乱样本顺序以避免出现过拟合的情况。

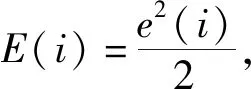
图2 Wine数据集损失函数仿真图像Fig.2 Loss function of Wine dataset

从图2可以看出，迭代到200次时误差收敛，表明WFBELC已经训练完成。

3.3.2 结果分析

仿真实验采用混淆矩阵来直观地反映数据集的分类结果，3个数据集的分类结果如图3所示。以Sonar数据集为例。图3(a)为利用Matlab中混淆矩阵函数生成的Sonar数据集测试结果，横坐标代表Sonar的2种实际类别，纵坐标代表预测的2种类别，图3(a)中第1行第2列数字4说明实际类别为1，预测结果为0的错误分类样本有4个。依此类推可知，Sonar数据集正确预测样本数为58，错误预测样本数为5，用于测试的样本共有63个，根据式(18)计算可得测试准确率为92.10%。同理，Wine数据集和Ionosphere数据集的测试结果见图3(b)和(c)。

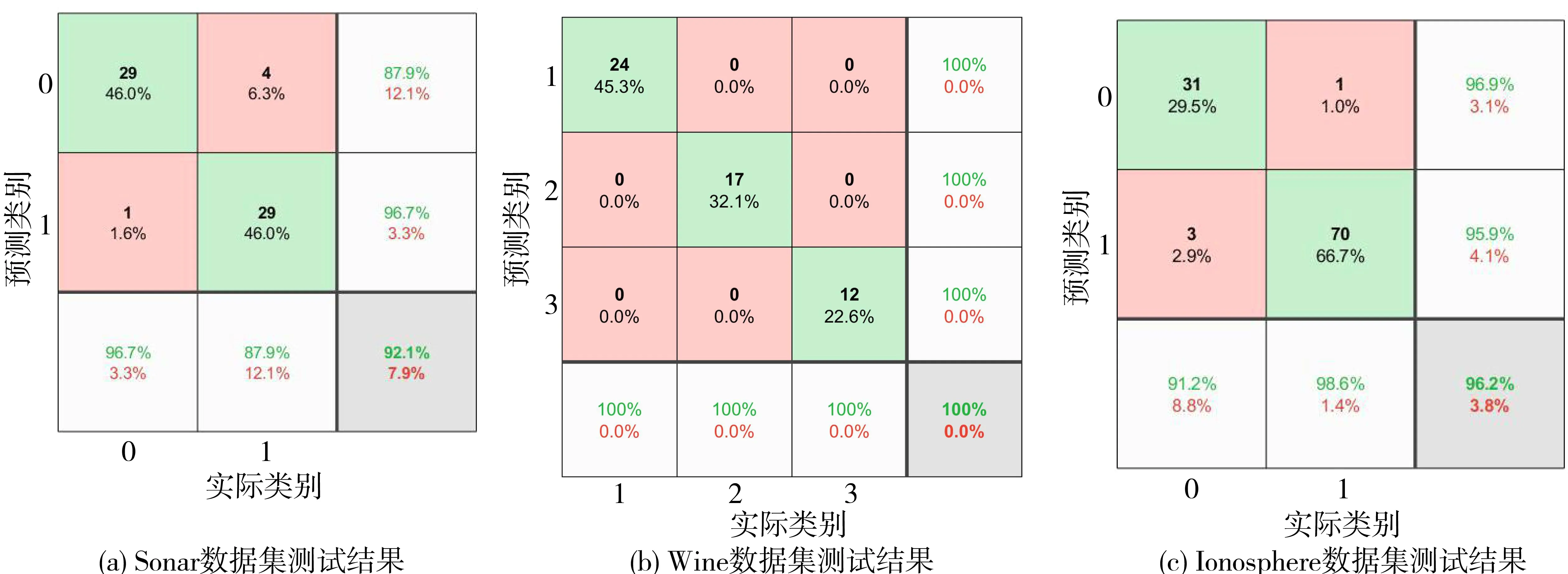
图3 3个数据集采用WFBELC仿真的混淆矩阵Fig.3 Confusion matrix of the three datasets by WFBELC simulation

为验证WFBELC的性能，将其与BP、FCMAC和FBEL 3种算法模型进行对比。表3为4种分类模型的分类准确率对比。由表3可知，WFBELC在Ionosphere、Sonar数据上准确率平均值为92.97%和86.19%，均高于其他3种模型；在Wine数据集上的准确率最大值达到100%，平均值为97.56%，也高于其他3种模型。由此可得，相比于其他模型，本文提出的WFBELC在数据集上的分类效果得到提升，证明了WFBELC用于数据分类的准确性。

表3 4种模型的分类准确率对比Table 3 Classification accuracy of four classification models compared 单位：%

3.3.3 与其他分类算法模型比较

为进一步说明WFBELC的性能，本文列出了近几年其他文献中采用相同数据集的算法模型的分类结果，具体如表4所示。由表4可知，对同一种数据集，WFBELC除在Ionosphere数据集的准确率平均值低于SVM模型0.13%，另2个数据集的准确率平均值均高于其他文献中的算法模型。通过表4数据的对比，进一步体现出WFBELC用于数据分类的优越性。

表4 WFBELC与其他文献算法模型的分类准确率对比Table 4 Classification accuracy of WFBELC compared with other literature algorithm models

4 结论

本文将小波函数作为模糊推理规则中的隶属函数，构成小波模糊大脑情感学习分类器。由于小波函数能敏感地反映突变信号且有良好的去噪效果，使得模型具有更快的学习能力和更好的泛化能力。将3个数据集应用于此模型，并与BP算法模型、模糊小脑模型(FCMAC)和模糊大脑情感学习模型(FBEL)进行对比。仿真结果显示，分类器在3个数据集上的分类准确率平均值均为最高，其中在Wine数据集上的准确率最大值达到100%，平均值为97.56%，表明基于小波函数的模糊大脑情感学习分类器具有较高的精度，可以作为分类决策中的一种工具。