Buck型DC-DC变换器的滑模预测控制方法

王 勇，高海燕

(厦门理工学院电气工程与自动化学院，福建 厦门361024)

Buck型变换器是DC-DC开关电源中最常用的电能转换器[1]，广泛用于计算机、精密仪器、通讯设备、工业制造、航天航空等领域[2-3]。传统的Buck型变换器采取的控制策略大多为线性的PID控制，该方法简单、容易实现。误差积分反馈的引入，虽然提高了系统响应的准确性，但闭环响应迟钝，容易产生振荡，且存在鲁棒性差、无法适应Buck型变换器的非线性特点等。近年来，大量非线性控制器被应用于Buck型变换器，如模糊PID控制[4]、自适应控制[5]、预测控制[6]、滑模控制[7]等。

1 Buck型DC-DC变换器的数学模型

Buck型DC-DC变换器的电路工作原理如图1所示。

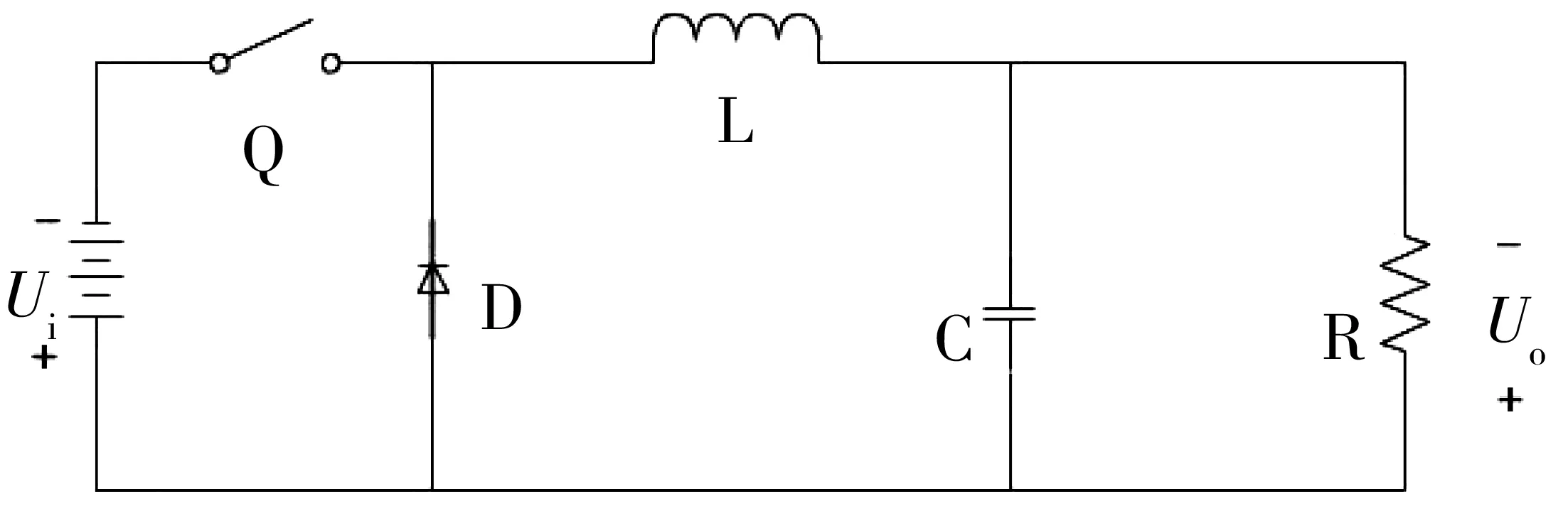
图1 Buck型变换器的电路工作原理Fig.1 Working principle of Buck converter circuit

Buck型DC-DC变换器有2种工作模式[15]，分别为连续工作模式(continuous conduction mode，CCM)和非连续导通模式 (discontinuous conduction mode，DCM)。在开关Q导通时，根据基尔霍夫电压电流定律，得到如下关系：

(1)

式(1)中：Ui为Buck型变换器电路输入电压；L为电感值；iL为流过电感的电流；Uo为电路输出电压；C为电容值；R为电阻值。

当开关Q断开时，根据基尔霍夫电压电流定律，得到如下关系：

(2)

在1个周期内，将2种状态进行合并，得到如下关系：

(3)

式(3)中：D∈[0,1]为占空比；定义期望占空比Us=Uv/Ui(Uv为期望输出电压)。选取状态变量x1=iL,x2=Uo，控制量u=D，方程(3)转换为如下状态方程模型：

(4)

记为

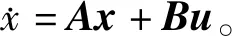
(5)

本文的控制目标是设计控制律，使得系统的输出电压Uo跟踪给定参考输出电压值，下节将解决这一问题。

2 Buck型变换器的滑模预测控制器设计

2.1 建立滑模预测模型

将式(5)进行离散化，可得：

x(k+1)=Ax(k)+Bu(k) 。

(6)

设期望参考输出信号为xd(k)，则跟踪误差信号为

e(k)=x(k)-xd(k)。

(7)

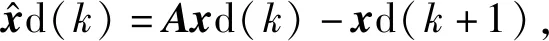
(8)

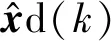
(9)

(10)

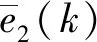
θ=[θ1θ2]=[θ2Kθ2]=θ2[KI]。

(11)

θ2的选取必须满足可逆的条件，滑模面可以由式(11)计算得到，因此得到滑模预测模型：

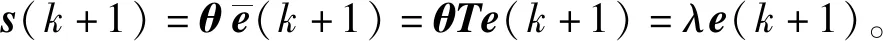
(12)

2.2 滑模预测控制器设计

定义无穷时域代价函数J∞(k)：

(13)

式(13)中：W和M为加权矩阵。

由于式(13)涉及到无穷时域的滑模函数s(k+i|k)和控制量u(k+i|k)，i=1,2,3,…,∞，求解将难以实现。为解决这一问题，需要经过一定的变换。

首先，定义二次函数：

V(e(k+i|k))=e(k+i|k)TPe(k+i|k)。

(14)

并且使其满足以下稳定性约束条件：

(15)

当控制系统稳定的情况下，s(∞|k)=0,u(∞|k)=0,将式(15)从i=0叠加到i=∞，可得到：

J∞≤V(e(k|k))≤γ。

(16)

式(16)中：γ>0为定义的无穷时域性能指标上界。这样，将求解无穷时域性能指标转化为求解γ的最小值，通过求解γ的最小值使J∞最小，令矩阵P=Q-1,将式(14)代入式(16)可得：

e(k|k)TPe(k|k)≤γ。

(17)

利用Schur补定理，可将式(17)写成如下矩阵形式：

(18)

e(k+1)=Ae(k)+Bu(k)。

(19)

假设控制率由状态反馈率和误差函数共同决定，即：

u(k+i|k)=F(k)e(k+i|k),i≥0。

(20)

将式(12)和式(20)代入式(15)中，得到：

e(k+i|k)T[(A+BF)TP(A+BF)-P+λTWλ+FTMF]e(k+i|k)≤0。

(21)

要使上式成立，只要：(A+BF)TP(A+BF)-P+λTWλ+FTMF≤0成立即可，令P=Q-1,Y=FQ代入，然后根据Schur补定理，可转化为如下线性矩阵不等式(linear matrix inequality,LMI)：

(22)

考虑输入约束，同样可以根据Schur补定理转化为如下：

(23)

因此，将式(13)转化为如下LMI求解问题：

(24)

综上，Buck型变换器的滑模预测控制器设计过程归纳为：

1)根据给定参考信号和当前时刻系统状态得到跟踪误差，将系统(3)转化为离散形式的简约误差状态方程(9)；

2)用极点配置法设计反馈增益K，选取可逆增益θ2，则简约误差系统的滑模增益为θ=θ2[KI]，得到误差系统的滑模增益λ=θT;

3)求解式(24)，得到最优解γ,X,Y,Q，状态反馈增益矩阵为F=YQ-1；

4)将计算得到的控制量D(k)=Fe(k)+Us，施加于系统(9)，令k=k+1；

5)重复步骤3)和4)。

3 仿真验证

为验证本文方法的可行性，在MATLAB中分别以Buck电路状态空间模型(4)和SIMULINK中搭建的实际模型为仿真对象进行分析。从式(4)可以看出Buck型变换器是线性的，而SIMULINK中搭建的实际模型有电容、电感、电阻、MOS管等元器件，MOS管的开和断是非线性的，因此模型是非线性的。为验证本文算法的优越性，将基于幂次指数趋近率的控制算法[7]、滑模预测控制算法[14]、预测控制算法[16]和本文的算法进行对比仿真。仿真中系统参数取值如下：输入电压Ui=36 V，电阻R=10 Ω,电感L=0.75 mH，电容C=50 μF，期望输出Uv=20 V,离散的采样时间Ts=0.05 ms,初始状态x(0)=[0 0]T。

输出电压波形、滑模面波形仿真结果如图2所示。

图2 输出电压波形、滑模面波形仿真结果Fig.2 Simulation results of output voltage waveform and sliding mode surface waveform

从图2(a)可以看出，本文的滑模变量平滑，不存在抖动。从图2(b)可以看出，采用本文的方法，系统输出电压能够以更快的速度收敛于期望值，动态响应好，且无超调量。从图2(c)可以看出，本文的算法对于非线性模型也适用，且控制效果与线性模型类似，均能以更快的速度到达期望输出电压，到达期望输出电压的时间分别为：本文算法0.12 ms；文献[7]中所用滑模控制算法0.52 ms；文献[14]中所用算法0.15 ms；文献[16]中所用预测控制算法0.25 ms；调节时间更短，验证该算法的可行性。

为验证本文算法在负载突变时的鲁棒性，在0.01 s时，将系统的负载变为4 Ω，此时各算法电压突变波形和电流突出波形仿真结果如图3所示。

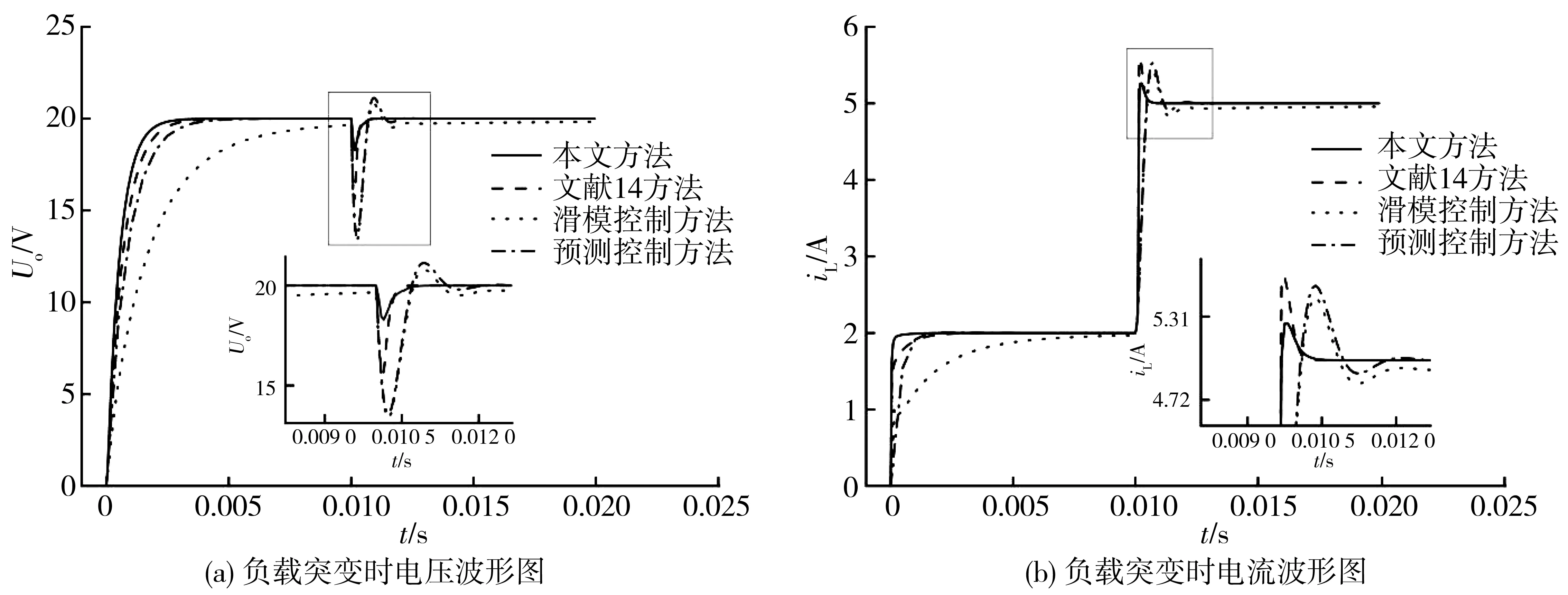
图3 负载突变时电压波形图和电流波形图Fig.3 Voltage waveform and current waveform in a sudden load change

从图3可以看出，系统在负载突变瞬间产生抖动，随后很快到达稳态值，且电压调节时间为0.43 ms，电流调节时间为0.11 ms，电压超调量为8.3%，电流超调量为3.2%，均小于其他方法，验证了本文方法在系统负载突变时的鲁棒性。

4 结论

本文研究DC-DC变换器的滑模预测控制方法，该方法首先将系统模型转化为误差状态方程，设计误差系统的滑模面，然后定义滑模面和控制量的加权求和为性能指标，最后通过Schur补引理，转化为优化问题。该方法将滑模控制与预测控制策略相结合，融合了滑模控制鲁棒性强和预测控制可以显式处理约束的优点，通过优化性能指标得到控制律，无需进行控制切换，因此，消除了滑模控制的抖振现象。仿真结果表明，相较于滑模控制、预测控制和已有的滑模预测控制方法，本文所设计的控制器调节速度分别提升76.9%、52.0%、20.0%，具有更快的调节速度；负载突变电压恢复到稳态的时间分别缩短0.40、0.13、0.03 ms，具有更强的鲁棒性，且完全消除了滑模控制的抖振现象。本文研究仅考虑简单的单相开关变换器电路，下一步考虑将本文算法推广到其他更复杂的三相Boost、Buck-boost等变换器电路中，并进行实际电路的样机实验。