用于三维点云识别的双模块图卷积网络*

王博豪, 孙战里

(安徽大学 电气工程与自动化学院, 安徽 合肥 230601)

0 引 言

近年来,随着激光雷达、深度摄像机等传感器的广泛使用,所捕获的三维(3D)数据越来越多,针对3D点云的研究分析也相应增多,因此,急需有效的算法来完成关键任务,例如点云分类[1,2]、分割[3]和其他3D形状分析任务等。

对于3D点云的分析,传统算法一般会结合一些估计的几何信息去建立模型,这些方法高度依赖人工制作的特征。在近几年中,开始有新的研究策略出现[4],许多研究也开始参考卷积神经网络(convolutional neural networks,CNN)在图像分析上的应用,将其应用在不规则点云的处理上。其中一种简单的策略是将点云转换为常规体素,还有一种是转换为多视图图像,以方便使用CNN，但这些转换通常会导致大量3D几何信息丢失,并且复杂度很高。PointNet是一项具有开拓性的工作,它可以直接处理原始点云而无需将其转换为其他形式[1],但它缺乏一些局部上下文信息。为了改进该缺点,PointNet++将点云层次化地分组为局部子集进行处理[2]。动态图CNN(dynamic graph CNN,DGCNN)在每一层产生的特征空间中通过计算欧几里得距离选出k个最近邻点来重建K最近邻(K-nearest neighbor,KNN)邻域图[5]。

本文提出在较高维特征空间中使用修正余弦相似度作为判别标准选出近邻的k个点构建KNN邻域图。另外,因为上述卷积层在进行每一次卷积时,使用的特征都是在前一层提取的基础上进一步学习,只能应用前一层特征,而在一定程度弱化了前几层网络层所学习的低维特征的作用,对此构建了一个残差特征学习模块,通过短连接多层基于网络并且固定图卷积特征尺度的方式改善这一点。

1 相关工作

多视图的方法会将3D形状转换为一系列2D图像的集合,然后应用传统的CNN。而体素方法是将3D形状转换为常规3D网格后,使用3D CNN[5]。但这种方法的参数量非常大,计算成本较高。

PointNet能够独立学习每个点的特征最后聚合全局特征,但其忽略了点云的局部信息[1],因此,PointNet++将点云划分为局部子集进行学习[2]。SO-Net提出了点云局部区域自组织网络[6]。PCNN(point convolutional neural networks)提出使用扩展算子和卷积算子组合对点云进行特征提取。此外还有利用全局特征的点云处理算法。

PointNet++利用传统的多尺度学习,直接在同一层捕获上下文,但这会大量增加计算复杂度[2]。ShapeContextNet采用了另一种形状上下文的策略搭建网络,使用自我注意力机制动态地学习所有点对的权重[7]。

2 算法介绍

2.1 网络整体结构

网络的整体结构如图1所示。

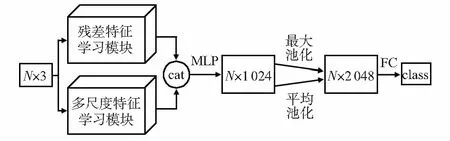
图1 网络整体结构

2.2 多尺度特征学习模块

引用DGCNN的模型[6],模块网络结构如图2所示。输入数据为点云P={xi︰i=1,2,…，N}∈RN×3,其中,N为点云所包含点的个数,xi表示第i个点的特征向量。点云数据在进入第一个KNN邻域图卷积层后,会输出维度为64的特征向量,随后进入下一层KNN领域图卷积,前2层的邻域图卷积都是基于欧氏距离进行构建,且特征维度均为64。到第3，4层图卷积层时,便采用基于修正余弦相似度的KNN(记为KNN-CS)邻域图卷积,此时所提取的特征也变为包含更丰富的语义信息的128维特征向量。在经过图2所示的4次KNN邻域图卷积后将多尺度特征做级联操作,得到维度为N×512的多尺度特征。

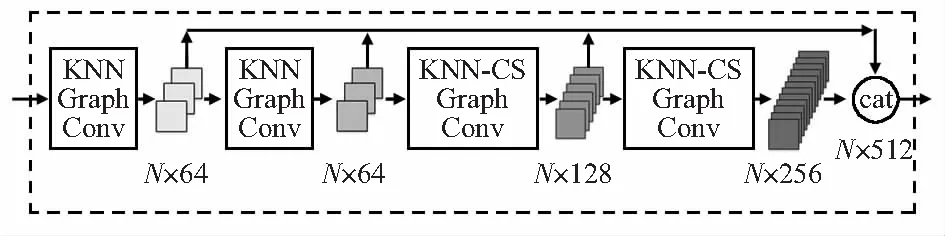
图2 多尺度特征学习模块

2.3 基于修正余弦相似度的KNN邻域图卷积

引用Spec-GCN的网络结构,实验所用的图卷积层模型如图3所示[8]。利用点云构建图G={V,E},其中,V={1,…,N},表示N个邻域图的顶点,E⊆V×V,表示图的边特征。点云中每个点xi都分别被视为顶点,再利用KNN寻找其邻域点xij(j=1,2,…,k),并以此构建出其邻域图(子图)。特征向量xi表示第i个点的3D空间坐标,因此,构建的KNN邻域图包含完全的3D坐标信息,随网络层的加深及特征维度的增多,特征会变成更高维抽象特征,此时采用修正余弦相似度进行KNN领域图的构建。

图3 图卷积模型

修正余弦相似度公式如下

(1)

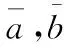
eij=xi-xij

(2)

经过下一网络层将邻域图的中心点特征及边特征编码成维度为N×k×D的更高维特征,表示为

F=hθ{cat(xi,Ei)}

(3)

式中h为所经过的网络层,θ为可学习参数,cat(xi,Ei)对特征xi和Ei进行级联。特征F经下一最大池化层,得到N×D的特征。

2.4 残差特征学习模块

引用MC-Conv的模型[9],用于点云的残差特征学习,如图4所示,共有4个KNN邻域图卷积层,最初的输入数据为点云坐标,进入KNN邻域图卷积层,经过MLP与最大池化层后得到N×64的特征,随后的3个图卷积层每一层的输入都是由上一层的输入和输出直接相加得到,可表示为

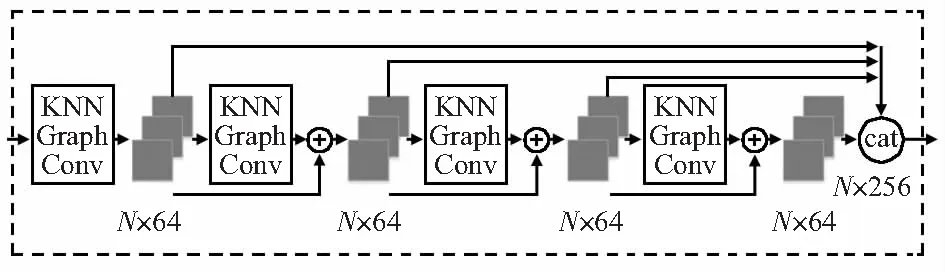
图4 残差特征学习模块

(4)

3 实验结果与分析

本文选用标准的公开数据集ModelNet40进行测试。数据集总共有12 311个物体,共包括40个类别，其中，9 843个模型用作训练数据集,其余2 468个模型为测试数据集。本文实验所使用的配置如表1所示。

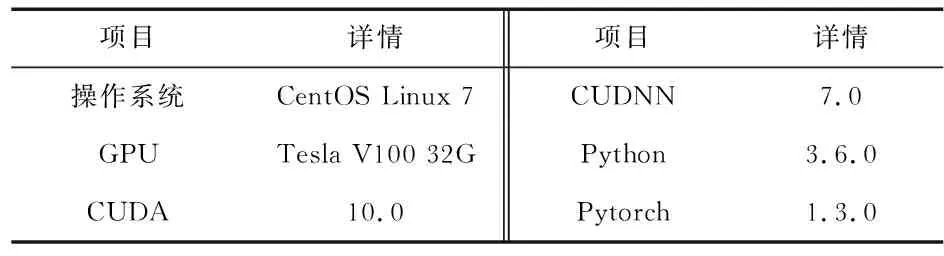
表1 实验配置

模型使用交叉熵作为损失函数,优化方法选用随机梯度下降法,其中的动量参数设置为0.9,权重衰减参数设置为0.000 4。学习率更新策略使用带有热重启的余弦退火算法,周期参数设置为100,初始学习率设置为0.2,最低学习率设置为0.000 4。迭代次数为400轮,训练批处理参数为40,测试批处理参数为20。在每个全连接层后都加入比例为0.5的Dropout,以抑制过拟合。

不同邻域点个数k对应的实验结果如表2所示,设置的k值分别为4,8,14,20,26,32。可以看出,当k为20时,能得到最佳实验结果。因为,较少的邻近点不足以提取出足够的局部空间结构信息,而当k过大时性能会发生退化。且较大的k会使得计算量大幅增加,实验花费时间成倍增长。

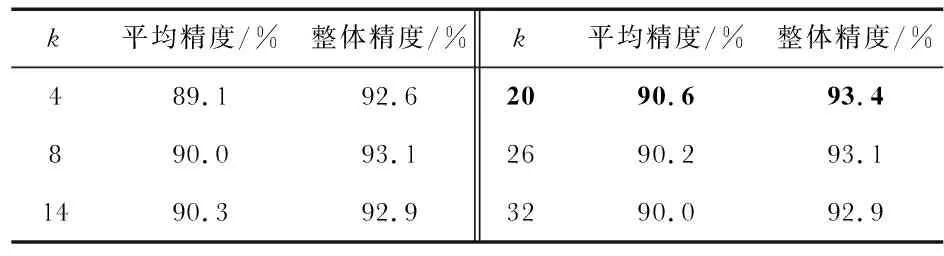
表2 不同k值的实验结果 %

鲁棒性实验结果如图5所示。点云的点个数分别设置为1 024,768,512,256,128,从图中可以看出,实验的整体精度与平均精度稍有下降趋势,但均无明显波动。且在选择128个点作为输入时仍能取得90 %以上的整体精度,甚至超过了PointNet使用1 024个点的整体精度[1]。足以证明本模型具有较强的鲁棒性。

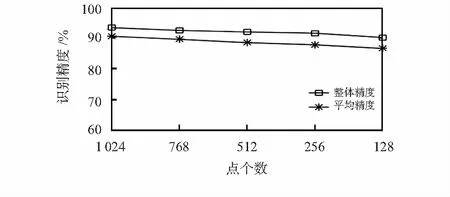
图5 鲁棒性实验

与其他文献的结果对比如表3所示,本文实验采用的输入数据为1 024个只含有3D坐标的点云数据,在表中将此类输入数据记为1×103,同理,2×103则表示输入点云数量为2 048,表中的5×103+nor 表示输入数据为5 000个点的3D坐标以及额外的法向量信息,表中的voting表示实验使用了多次投票验证策略。从表中可以看出,在输入点云的数量为1×103时,本文实验的平均精度和整体精度均优于其他文献。此外,PointNet++[2]与SpiderCNN[10]还使用了5×103数量级别的点云并添加了额外的法向量特征,但实验精度仍然较低。RS-CNN在使用了多次投票验证策略后,得到了93.6 %的实验整体精度,但在不使用该策略时的整体精度为92.9 %,低于本文的93.4 %。表3中的实验结果可以证明,本文网络模型的有效性。

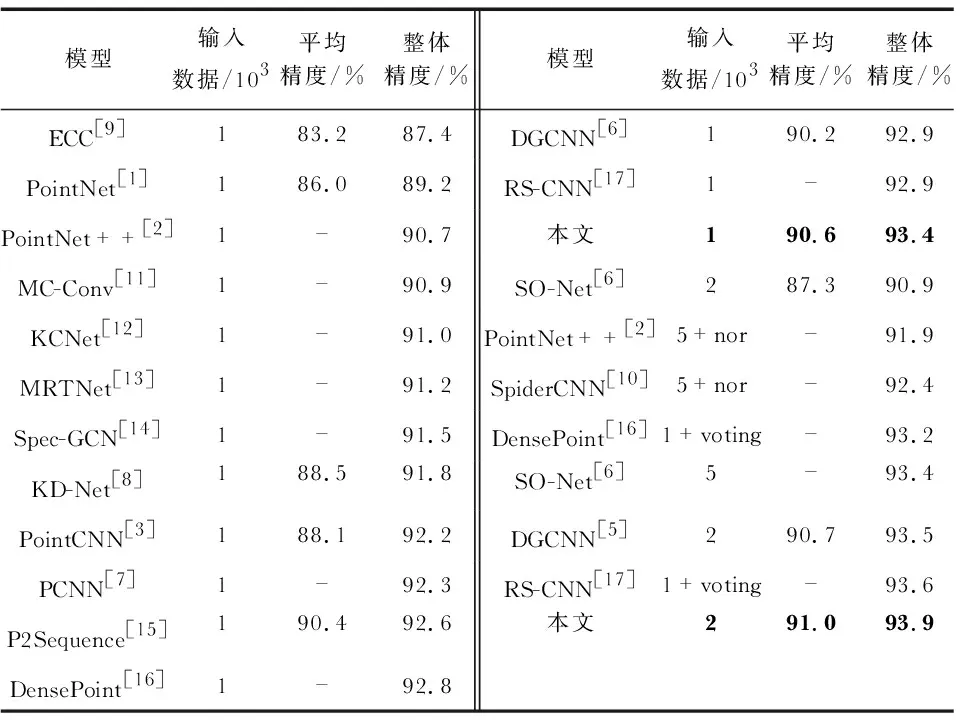
表3 在ModelNet40数据集上实验结果对比

4 结束语

本文提出了一种用于点云识别的双模块图卷积网络。两个不同的模块分别用于提取点云的多尺度特征和残差特征,然后将两种特征融合后经过多层感知机、池化层以及全连接层,最终得到点云的类别。在ModelNet40数据集上的分类任务实验结果表明了本文算法的有效性。下一步工作将考虑对网络模型作进一步优化,并扩展到其他任务场景,例如点云分割、配准等。