基于GA–BP神经网络的汽车内饰板虚拟制造研究
张德海,付亮,李艳芹,李军恒,祝志逢,黄子帆
基于GA–BP神经网络的汽车内饰板虚拟制造研究
张德海,付亮,李艳芹,李军恒,祝志逢,黄子帆
(郑州轻工业大学 机电工程学院,郑州 450002)
以某汽车内饰板为研究对象进行虚拟制造,以提前得到相对准确的工艺参数并减少成形缺陷的产生。研究了工艺参数对产品拉延成形质量的影响,并确定了拉丁超立方抽样区间,在抽样区间内抽取60组样本数据,以最大减薄率为目标值,以前50组样本数据为测试集、后10组样本数据为预测集,使用基于GA–BP神经网络的遗传算法得到最优工艺参数,并将其代入有限元分析软件DYNAFORM中进行虚拟制造。训练后GA–BP模型的预测值与期望值最大误差为0.299 7%,最大预测误差率为1.747 38%;遗传算法预测的最大减薄率为16.548%,虚拟制造得到的减薄率为16.167%,虚拟制造值与预测值的大小仅相差0.318%,仿真误差的误差率为2.36%。虚拟制造结合先进算法的优化方法可以指导后续生产。
DYNAFORM;GA–BP神经网络;内饰板
内饰板产品越来越多地应用在汽车、航天、交通等领域中,其往往采用薄板冲压的方式进行成形。有些产品因为表面形状复杂、成形工艺烦琐等多方面因素的影响,在成形过程中经常会出现起皱、破裂、回弹、成形不足等质量缺陷。这些缺陷往往是由多个因素引起的,因此难以通过控制某个因素来解决问题,通常要同时对多个参数进行调整。为找到相对合理的工艺参数,往往采用“试错法”来调整成形时的工艺参数,但这种方法要消耗大量的人力、物力和时间[1-3]。
近年来,随着计算机技术的发展,数值模拟及智能制造技术得到了广泛应用,先进算法结合虚拟制造的优化方法可以得到相对准确的工艺参数并减少成形缺陷的产生。近年来,国内外学者对此类交叉问题进行了深入探讨,并进行了大量探究。孙慧等[4]为解决拉伸件在拉深过程中出现的起皱问题,通过正交实验得到了最佳工艺参数的组合。徐小娟等[5]以铝合金板料的自冲铆接工艺为分析对象,以正交实验和方差分析为手段,确定了各工艺参数对底切量影响的主次顺序,并得出了最优的工艺方案。臧其其等[6]以DYNAFORM为基础,对某轿车铝合金地板梁的拉延成形过程进行了仿真,根据仿真结果对拉延参数进行了优化,最后得到了符合质量要求的产品零件。王康康等[7]使用DYNAFORM与神经网络相结合的方法,以汽车行李箱内板为研究对象,以最大减薄率为目标,得到了最优工艺参数。刘强等[8]利用DYNAFORM对空调压缩机壳冲压成形过程进行了仿真实验,利用仿真获得的实验数据训练径向基函数(RBF)神经网络,并结合遗传算法(NSGA–Ⅱ)和逼近理想排序法(TOPSIS)进行评价筛选,得到了产品的最优工艺参数。Zhang等[9]利用DYNAFORM软件对压边力、毛坯形状和毛坯尺寸进行了仿真计算,并采用数值模拟和实验相结合的方法解决了飞机蒙皮双曲率薄壁铝合金件(DCTAP)在成形过程中圆角不饱满、裂纹和起皱等问题。崔学习等[10]采用冲压成形工艺和电磁成形工艺相结合的方法,获得了成形覆盖件的最佳工艺参数,解决了铝合金材料在冲压时回弹量过大、流动性差等问题。Ma等[11]以汽车下层板为研究对象,研究了BHF(空白支架力)、模角半径、摩擦因数和模具间隙对最大减薄率和最大增厚率的影响,并在此基础上对4个参数进行了优化,获得了优质产品。上述研究主要集中于使用DYNAFORM软件进行数值模拟,并结合遗传算法、正交实验等方法得到最优工艺参数,而文中将采用基于GA–BP神经网络的遗传算法与DYNAFORM数值模拟相结合的方法对工艺参数进行优化,并将预测值与仿真值进行对比,以验证此方法的准确性。
为得到最优工艺参数、降低在设计阶段的人力物力、减少实验阶段的成本,文中以DYNAFORM软件为平台,建立GA–BP神经网络模型,通过遗传算法寻找最优解。主要步骤如下:首先通过设计的仿真实验探究压边力、冲压速度、摩擦因数、拉延筋阻力占比等参数对成形质量的影响规律,从而得到最优工艺参数范围;其次用拉丁超立方抽样的方法抽取60组样本数据,以此数据为原始训练数据构建精准的GA–BP神经网络模型,再用智能算法对全局寻优得到最优工艺参数;最后通过虚拟制造验证其准确性。
1 内饰板的工艺分析
内饰板形状如图1所示,零件尺寸为316 mm× 1 450 mm×1.2 mm,通过对其进行工艺分析,确定工序为拉深、修边、冲孔。材料选用DYNAFORM材料库中的HRDQSK,材料性能参数如表1所示,硬化曲线如图2所示,FLC曲线如图3所示。分析零件可知,零件的上部有较长的凸起部分,在冲压时容易发生破裂,左侧有几字形凸起,在成形过程中,此处极易因厚度变薄而导致破裂,右下侧也有一部分倒角,这些部位在冲压时容易破裂。产品整体没有较大的曲率,因此零件在拉伸时较少涉及回弹,零件需要在DYNAFORM软件中进行工艺补充以及压料面的设计。几字形凸起及设计后的内饰板如图4所示。

图1 内饰板形状
表1 材料性能参数

Tab.1 Performance parameters of materials
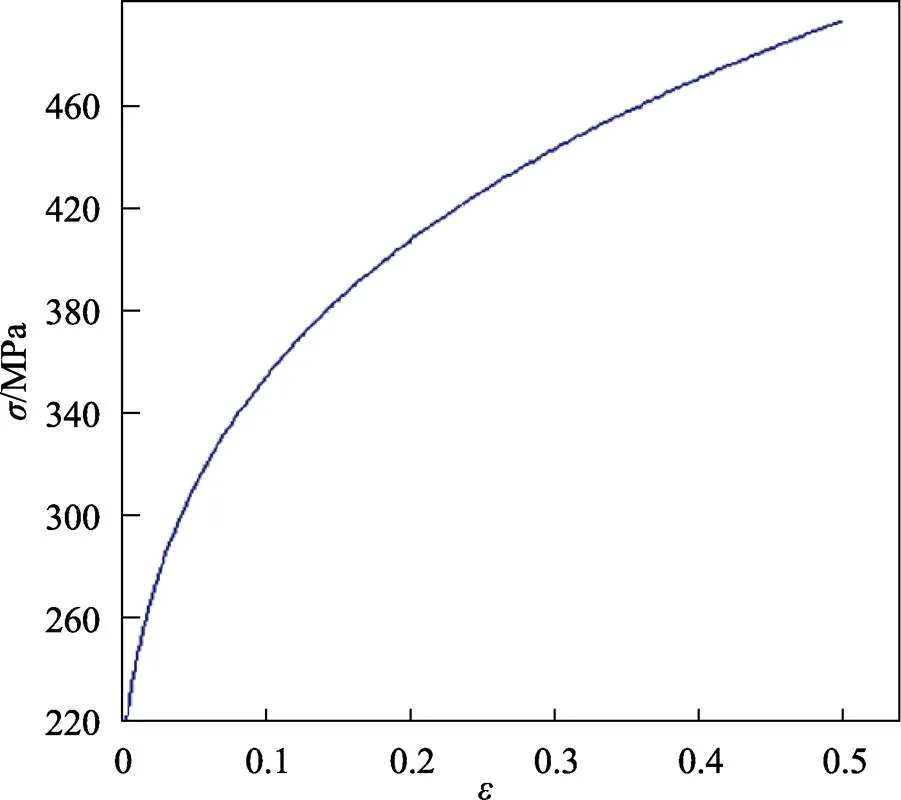
图2 硬化曲线
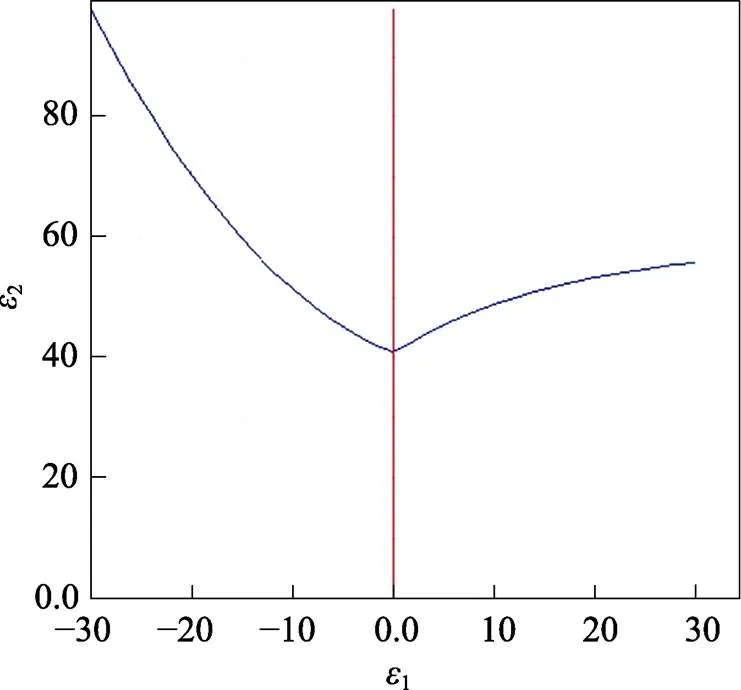
图3 FLC曲线
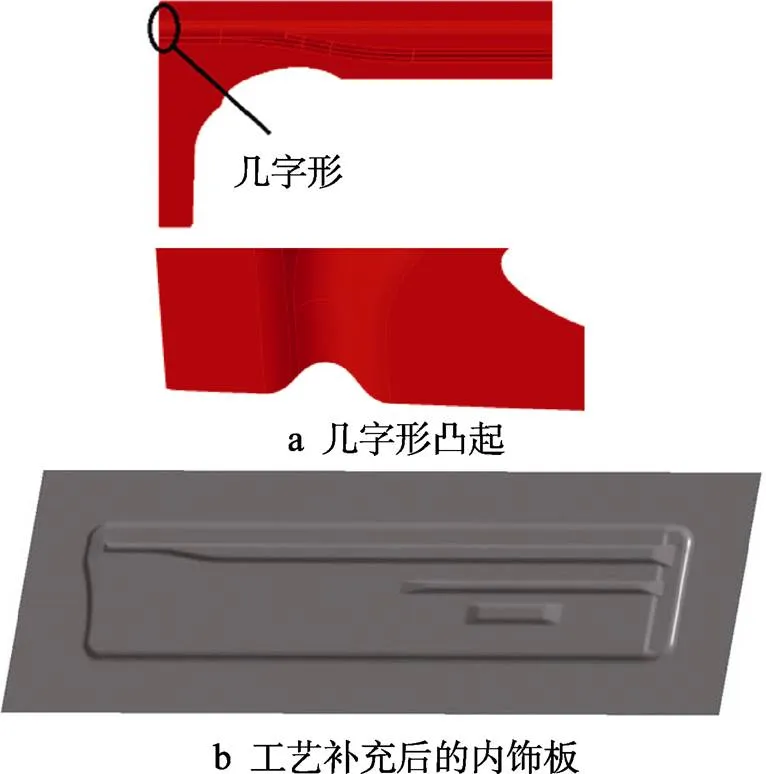
图4 几字形凸起及工艺补充后的内饰板
设计后的产品可通过DYNAFORM得到拉延模具,其仿真模型如图5所示。工艺补充面有大部分为平面,需设计拉延筋,据经验设计的拉延筋位置如图6所示。成形工序为单动拉延,板料采用壳单元,在划分网格时,板料网格划分为4 mm,材料模型选择36号材料[12],模具设置为不变形的刚体,划分网格为5 mm。
对于隐藏层,有:
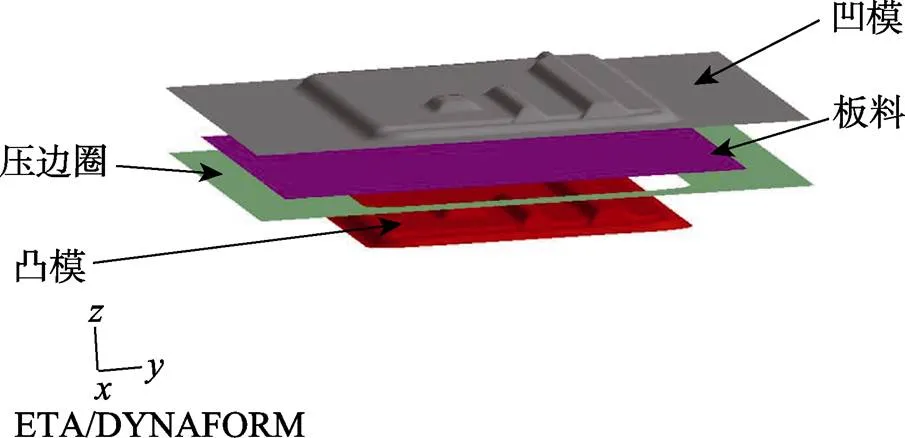
图5 零件仿真模型
2 不同工艺参数对成形质量影响
为增加GA–BA模型的准确度,使后续遗传算法的全局搜索更加准确,得到更为合适的压边力、冲压速度、摩擦因数、拉延筋阻力占比,研究不同工艺参数对成形质量的影响非常必要。文中通过将4个工艺参数分成不同梯度来研究工艺参数对拉延成形的影响,以得到GA–BP模型最为合适的参数范围。

图6 拉延筋设置
2.1 不同工艺参数初步选取
超立方抽样是一种广泛应用于解决工程问题的随机抽样的实验设计方法,其特点是抽样点分布均匀,可以在较少的抽样样本下,快速地达到计算收敛[15-18]。根据2.2节确定的各参数范围,使用拉丁超立方的方法在抽样区间内抽取60组样本数据,然后以此样本点为数据库来构建GA–BP神经网络模型。其中,以前50组样本数据为测试集、后10组样本数据为预测集。
表1中的数据为样品未经任何预处理而进行的色谱和滴定分析结果,由分析数据来看,其主成分双乙烯酮和醋酐的含量均有较大差距,下面结合表2和表3中数据作进一步的分析。
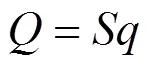
式中:为压边力,kN;为单位面积的压边力,MPa,一般为2~4.5 MPa;为压边圈下板料投影面积,mm2。经测量,≈670 000 mm2,=2 MPa,所以拉延时的压边力约为1 350 kN。
摩擦力可以控制材料的流动情况,是影响成形质量的一个关键因素。根据经验及文献[14],摩擦因数取0.12,初次冲压速度取1 000~7 000 mm/s,适当地设计拉延筋可以很好地处理局部拉延不足等问题,故拉延筋阻力占比(此时拉延筋阻力占完全锁死时拉延筋阻力的百分比,下同)取25%左右[14]。各参数设定如表2所示。
2.2 不同工艺参数仿真分析
通过DYNAFORM对表2中的数据进行仿真,通过分析仿真后各组的FLD图得到不同工艺参数对板料成形质量的影响,如图7所示。
该阶段企业己识别生产活动和生产环境中的风险和问题,初步编制并形成了的安全管理的标准和要求,同时,己组建与生产组织和管理部门并重的安全主管部门,负责组织、实施、改进安全管理工作、优化和持续完善完全管理标准与制度。在该阶段,安全管理工作的主要特征是自上而下单向为主。主要表现在:安全主管部门负责编制和形成安全标准和实施规范,业务部门和人员负责执行;安全主管部门负责发现问题和隐患,业务部门和人员负责整改和落实;安全主管部门负责提出安全知识和能力要求并组织培训工作,业务部门和人员负责参与培训和接受培训。该阶段工作组织方式可以称为以安全主管部门为中心的安全管理体系,见图2。
由图7a可知,当压边力增大时,最大减薄率呈先增大后减小的趋势,当压边力为1 200 kN左右时,最大减薄率较小,因此在后续拉丁超立方抽样时,压边力选取区间为800~1 600 kN。随着摩擦因数的增大,最大减薄率呈上升趋势,最大值为27%,摩擦力的大小可以影响板料流动的快慢进而影响板料成形质量[6],根据图7中最大减薄率的变化趋势,选取摩擦因数为0.06~0.15进行拉丁超立方抽样。随着冲压速度的增大,最大减薄率呈先增大后减小的趋势,分析可知,冲压速度的拉丁超立方抽样区间为4 000~7 000 mm/s最为合理。当拉延筋阻力占比为29%时,减薄率最小,故拉延筋阻力占比的拉丁超立方抽样区间设置为25%~34%。分析图7b可知,在冲压仿真时,板料的最大增厚率为2.4%。
遗传算法(genetic algorithm,GA)是1957年由美国Michigan大学的Holland教授及其科研团队提出的,算法的原理是通过模拟达尔文生物进化论中“优胜劣汰”的自然选择和进化机制来构造计算模型[20-23],其主要特点是可以实现快速全局搜索。其主要原理将问题编码成染色体,染色体上不同的位置代表不同的基因,不同基因会控制不同的表现型,在优化时,不同位置的基因会发生选择、交叉、变异等操作,然后将适应度好的基因遗传到下一代、适应度差的基因淘汰,经过多次迭代,最后的适应度结果将无限接近理论最优值。
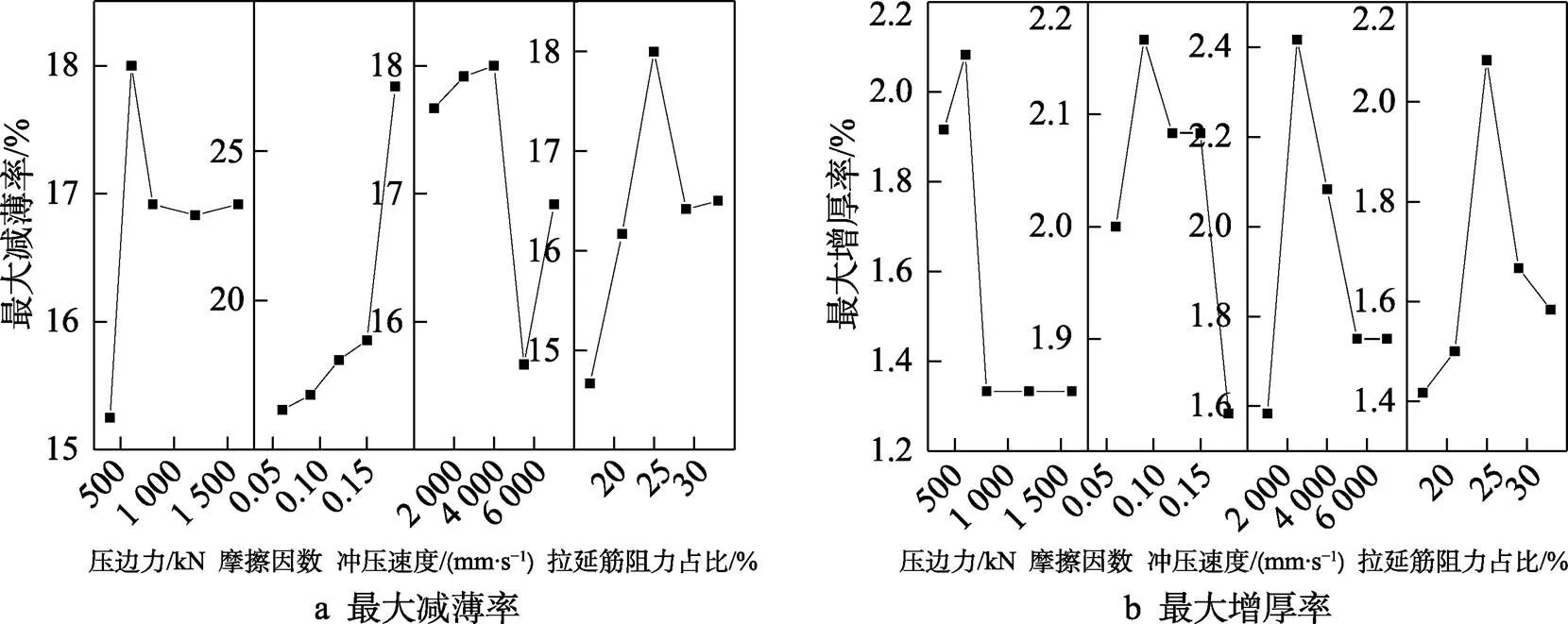
图7 不同参数下的成形质量
表2 各参数设定
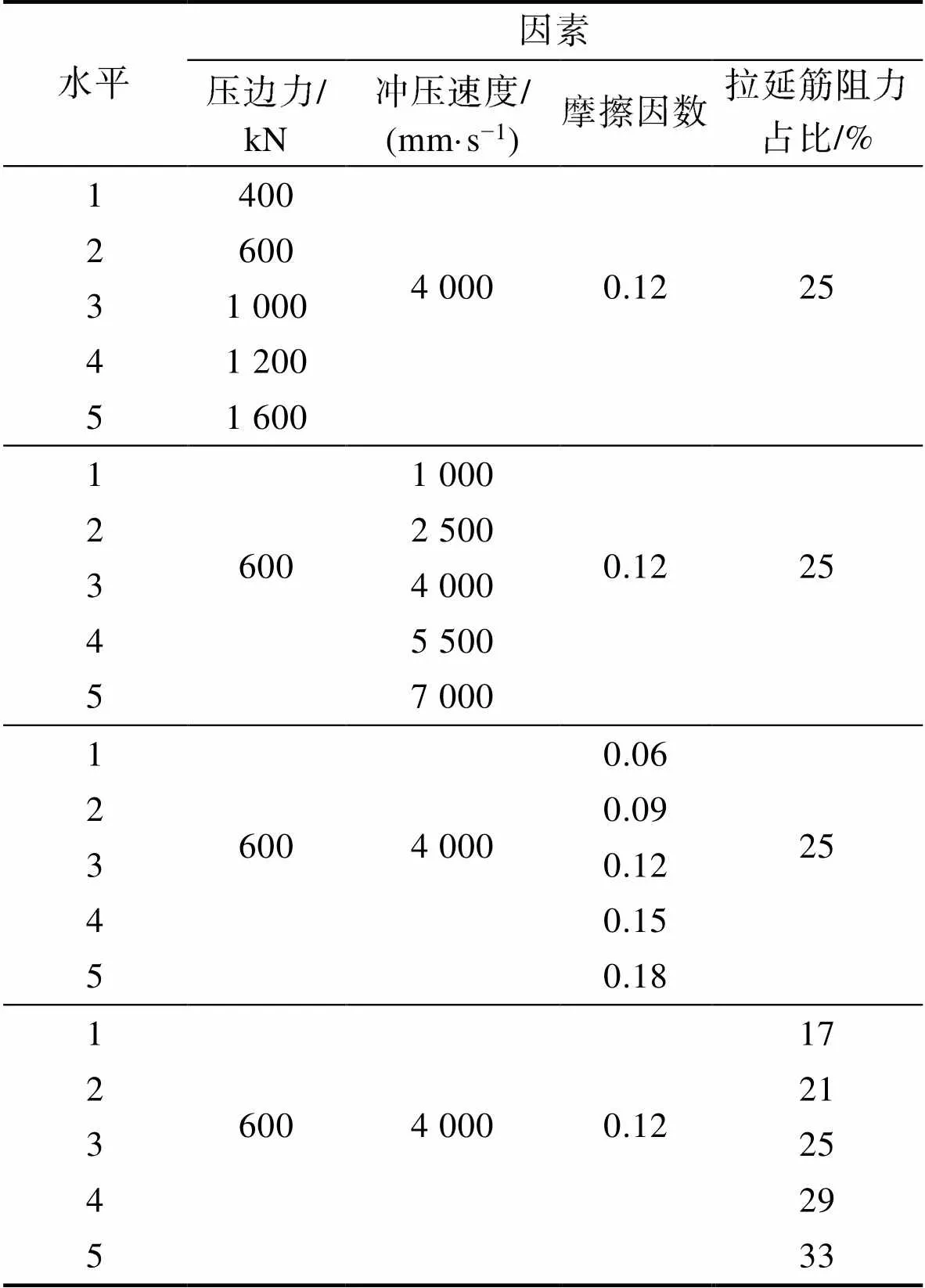
Tab.2 Setting of each parameter
当压边力为600 kN、冲压速度为4 000 mm/s、摩擦因数为0.12、拉延筋阻力占比为25%时,FLD图中的厚度变化情况如图8所示。可知,板料成形时凸起部位即①处厚度变化最为明显,此处有破裂的风险;起皱以及起皱趋势出现压边圈以外的区域②处。当工艺参数变化时,最大减薄率和最大增厚率也将跟着变化。为使最大减薄率、最大增厚率最小,将通过数值模拟与智能算法相结合的方法得到最优的压边力、冲压速度、摩擦因数、拉延筋阻力占比。
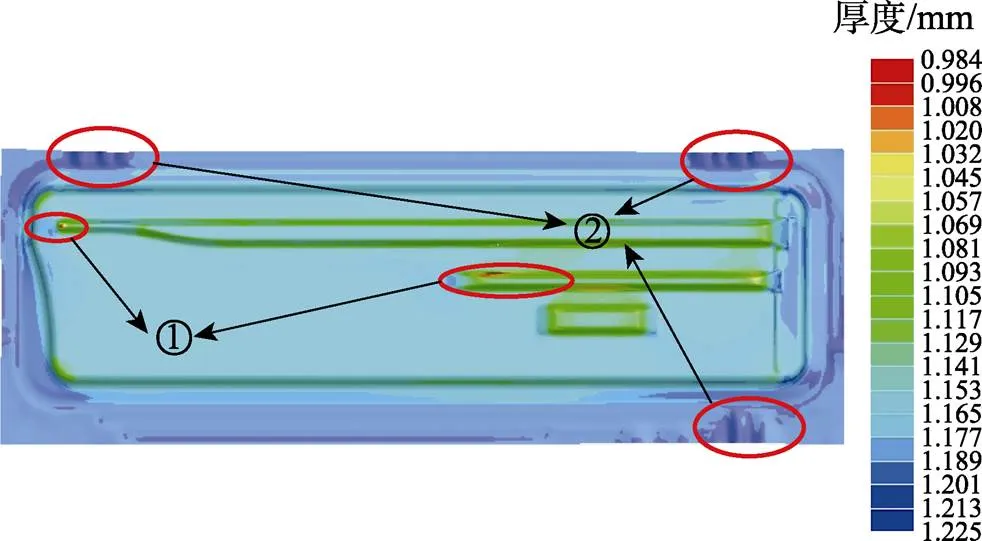
图8 FLD图中的厚度变化情况
3 基于GA–BP神经网络的遗传算法的参数优化
3.1 拉丁超立方抽样
成形工艺中进料的阻力大小会影响成形质量。压边力的大小可根据式(1)[13]来计算。
3.2 GA–BP神经网络模型的建立
BP神经网络又称误差反向传播(back propagation)神经网络,可以实现输入层到输出层任意的非线性映射。在神经网络中,输入为正向传播,误差为反向传播,训练方式是通过得到输出层的响应值y与期望值的误差D,并基于误差反向传播逐层训练其中的权值[19]。BP神经网络结构模型如图9所示,该模型由输入层、隐藏层、输出层3层结构组成,主要参数包括输入层数据x、输入层到隐藏层权值矩阵1、隐藏层输出变量m、隐藏层到输出层权值矩阵2、输出层参数y。
王蒙在一篇文章中,也说到个人尺度问题。他说:“上一代人对下一代人的消极评价,究竟有多少是靠得住的?有多少是以己度人度量出来的?反过来说,下一代不是也以自身当标尺吗?”意思是说,世事与时俱进,一切都在变化,评判是非的尺度不能停步不前,当然,对前人的有些好东西,还要珍惜和继承。因此,无论上代人,还是下代人,只要自己评判是非的尺度错了,就要自觉改正才好。
继发性帕金森病;除阴虚风动型外的其他证型帕金森病;心肺肾等功能严重损伤;中枢神经系统严重病变;孕期哺乳期;具有滥用药史和酗酒习惯。
本文从歌词的语言出发,通过两首典型“中国风”歌曲歌词修辞格运用的分析,试探究修辞格的不同运用给“中国风”歌曲带来的效果。试着通过对同一类型歌词修辞格运用的研究,来探索“中国风”歌曲对修辞格态度的异同以及由此带来的效果对歌曲的影响。
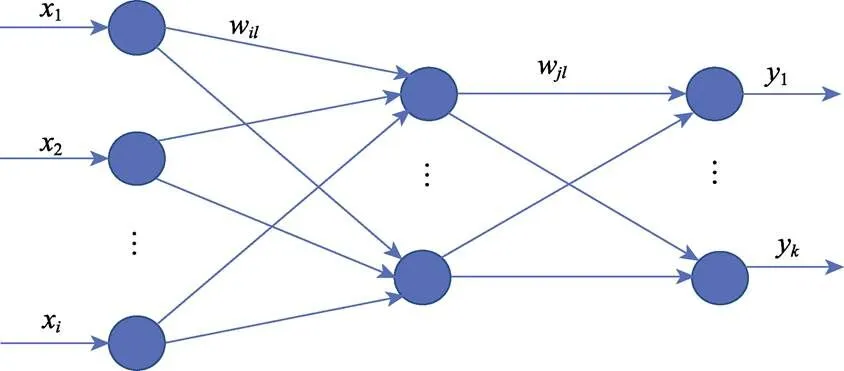
图9 BP神经网络结构
BP神经网络传递的基本原理如式(2)—(3)所示。
GA–BP神经网络模型的原理主要是使用遗传算法对神经网络的权值和阈值进行优化,然后将优化后的权值和阈值代入遗传算法中,以大幅度提高神经网络的准确性以及稳定性。GA–BP神经网络模型由BP神经网络的确定、遗传算法的优化、遗传算法的预测3部分组成[24]。GA–BP流程图如图10所示。
虽然国别与区域研究在外语学科的地位得到了确立,但是外语界对它的认识和接受经历了曲折发展的过程。笔者的个人经历就很好地反映了这一点。
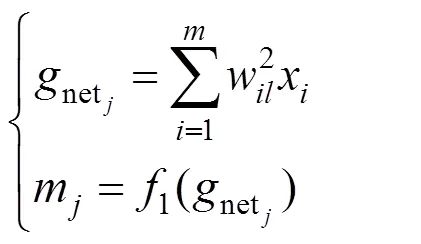
对于输出层,有:
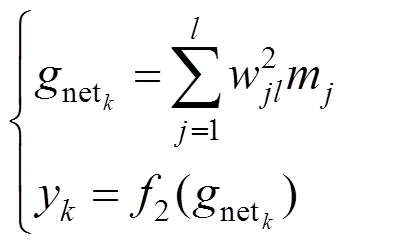
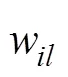
结合案例,因新模式增加了投资和融资,产生了财务杠杆。同时,提高经营杠杆至4.79倍,但低于同行业平均水平。因此,风险较低,较之旧模式提高综合杠杆2.02倍,EBIT提高9%,节税效果明显,利于公司发展(表10)[1]。
在GA–BP神经网络模型神经网络的确定部分中,神经网络中待优化参数为压边力、冲压速度、摩擦因数、拉延筋阻力占比,以待优化参数为神经网络中的4个输入层节点,以仿真FLD图的最大减薄率为神经网络输出值,因此神经网络有1个输出层节点,并设置10个隐含层节点。在训练神经网络时,以拉丁超立方抽样的前50组样本数据为训练数据、后10组样本数据为测试数据。在遗传算法优化部分,以神经网络的预测值和期望值的绝对值为遗传算法的适应度,经过遗传算法的反复迭代,将最优适应度所对应的权值和阈值返回给神经网络中,从而得到最为精确的GA–BP神经网络模型。神经网络的部分参数设置如下:训练次数为3 000,学习率为0.1,训练目标为0.001。遗传算法的部分参数设置如下:迭代次数为200,种群规模为80,交叉概率为0.3,变异概率为0.1。
最终拉丁超立方抽样区间设置如下:压边力为400~1 600 kN、冲压速度为4 000~7 000 mm/s、摩擦因数为0.06~0.15、拉延筋阻力占比为25%~34%。
使用SPSS23.0软件,计量资料用均数±标准差描述,计数资料采用构成比描述,以双侧P<0.05为差异有统计学意义,计量资料根据资料方差的齐性,使用独立样本t检验;计数资料用χ2检验。若P<0.05则纳入多因素Logistic回归方程,分析其对预后的影响,作查尔森合并症指数以及其他与术后5年生存率相关因素的受试者工作曲线(ROC曲线)。
在训练BP神经网络时,可以通过判断输出值与期望值的误差,反向调整权值矩阵,但由于权值初始值的取值范围一般为0~1,因此在网络训练初期权值波动较大,这将导致BP神经网络学习效率低、收敛过慢。
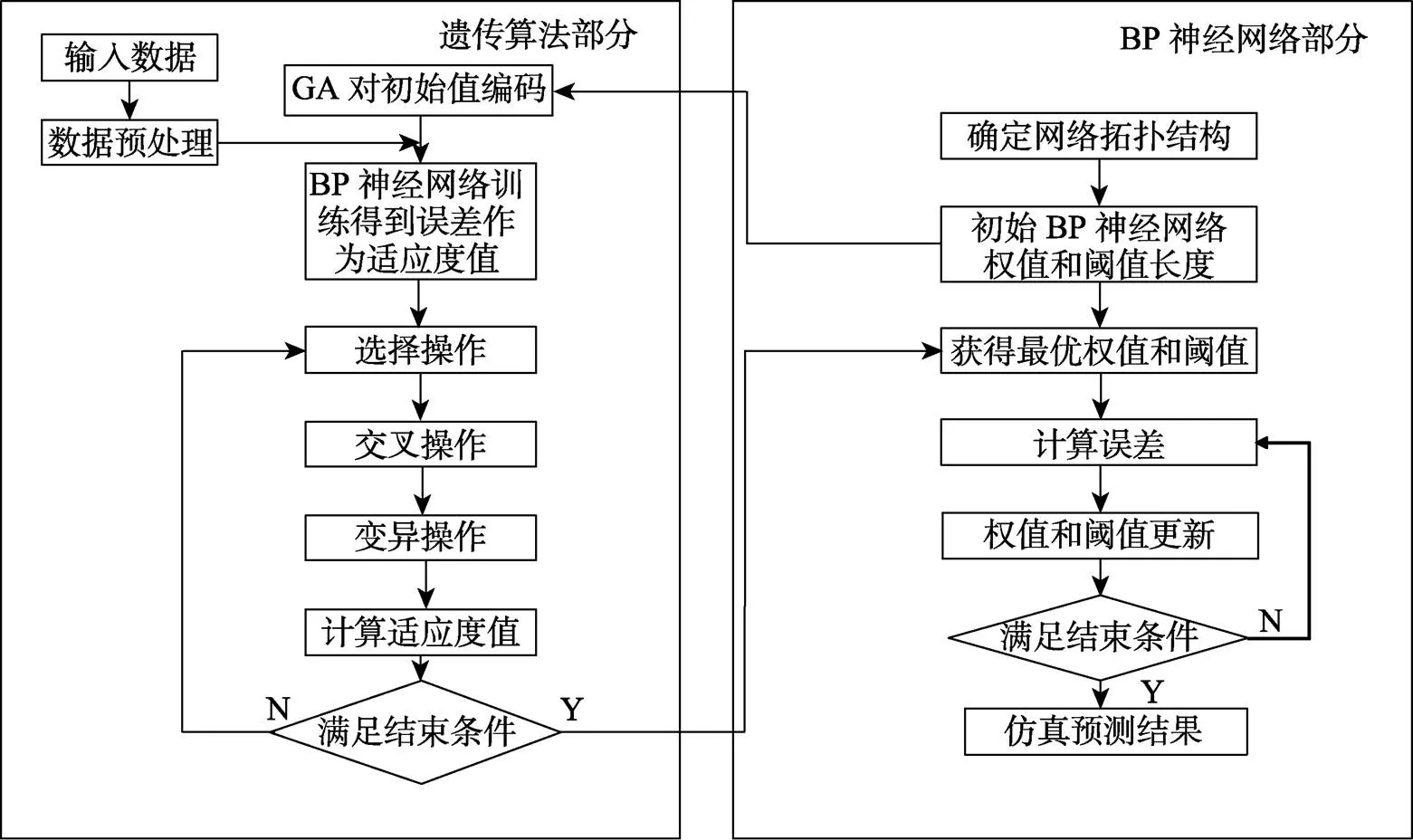
图10 GA–BP神经网络流程图
3.3 GA–BP神经网络模型的训练
将拉丁超立方抽样的样本数据代入GA–BP神经网络模型中进行训练,模型训练时的最佳验证误差曲线如图11所示,由图11可知,第9代的最佳验证误差为0.044 536。模型训练的相关性回归结果如图12所示,由图12可知,训练集的回归预测值为0.938 82,验证集的回归预测值为0.918 46,测试集的回归预测值为0.826 79,模型精度高达82.679%。
训练完成的GA–BP神经网络模型最大减薄率的预测值与期望值的对比以及预测值误差率如图13所示。由图13可知,最大减薄率的预测值与期望值的最大误差为0.230 5%,最大预测误差率为1.328 3%,由此可见,所建立的GA–BP神经网络模型准确,可以用来预测板料成形的最优工艺参数。
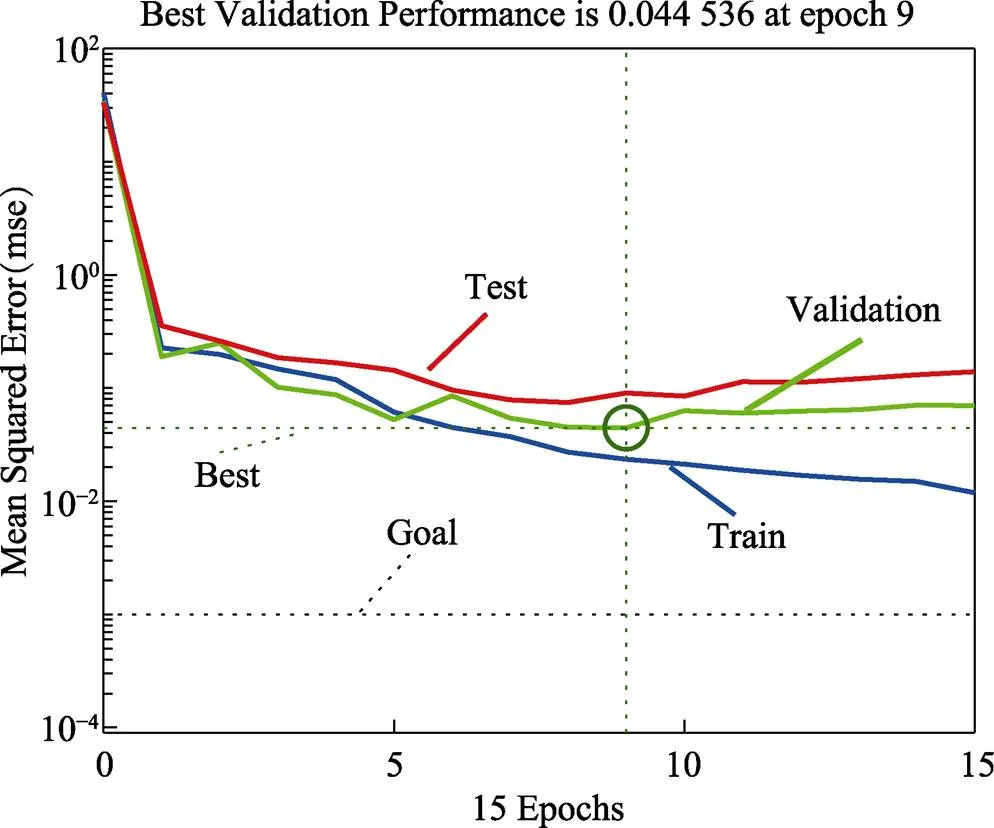
图11 GA–BP模型的最佳验证误差曲线
以训练后GA–BP神经网络的输入值(压边力1、冲压速度2、摩擦因数3、拉延筋阻力占比4)和预测值为遗传算法中的个体,以预测值为遗传算法的适应度值,经过遗传算法的选择、交叉、变异,使适应度值达到最优,此时可得到最优适应度对应的个体,即得到最优工艺参数压边力1、冲压速度2、摩擦因数3、拉延筋阻力占比4。遗传算法模型()如式(4)所示。
矩阵Rbe反映了足端坐标系到机身坐标系的旋转关系,三维矢量Pbe反映了足端在机身坐标系中与质心的位置关系,两者共同体现了机器人足端的位姿。
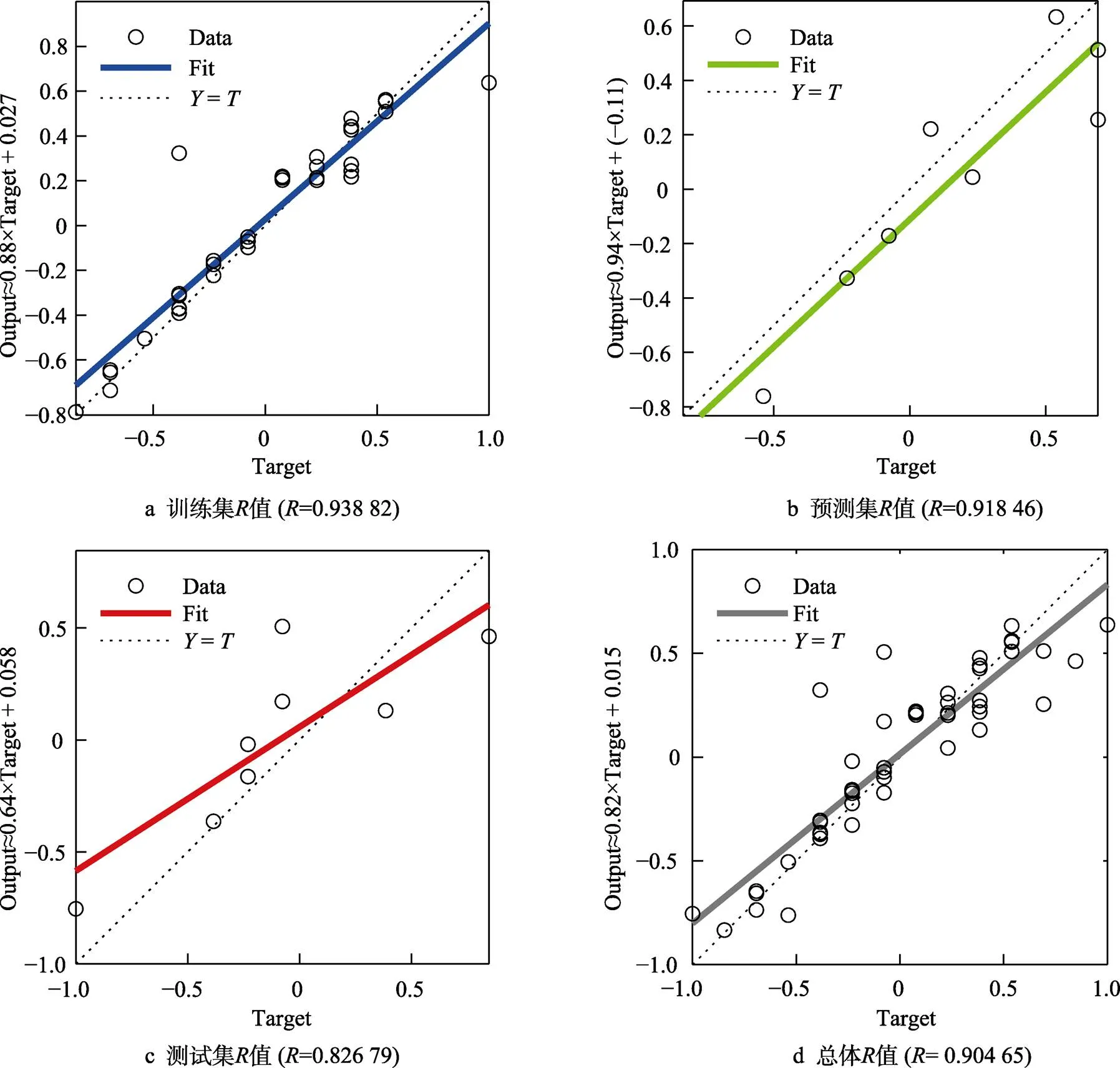
图12 GA–BP模型训练相关性回归结果

图13 GA–BP神经网络最大减薄率的预测值与期望值对比及预测值误差率
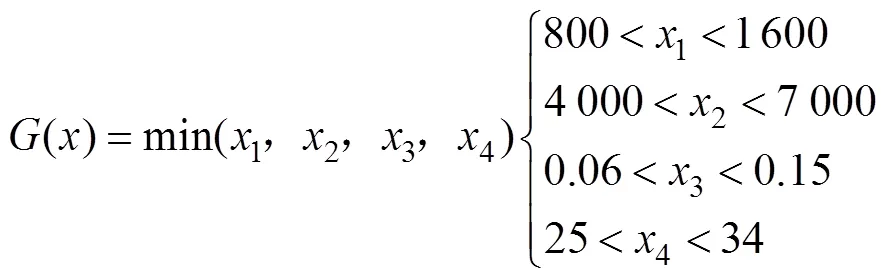
最优个体适应度曲线如图14所示。可以看出,迭代后得到的最优适应度即最大减薄率的最小值收敛于16.548%,此时对应的最优参数如下:压边力为1 251.06 kN、冲压速度为6 209.20 mm/s、摩擦因数为0.06、拉延筋阻力占比为28.18%。
将基于GA–BP神经网络遗传算法优化的输出参数带入DYNAFORM软件中进行数值模拟,得到的厚度变化情况如图15所示。由图15可以看出,仿真结果的最小厚度为1.006 mm,计算得到减薄率为16.167%,与基于GA–PB神经网络遗传算法的预测值大小仅相差0.318%,仿真误差的误差率为2.36%,这表明基于GA–PB神经网络遗传算法的优化方法准确性非常高。整体内饰件在拉延过程中都处于安全区内,所得的结果符合生产实际要求。
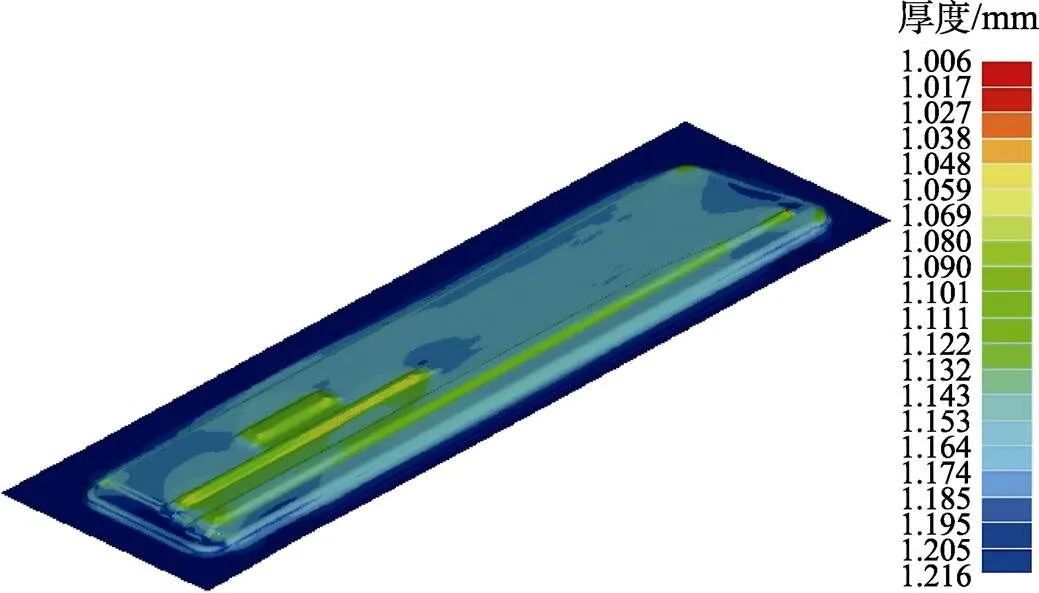
图15 优化后的厚度变化
4 结论
1)针对内饰板拉延时易导致破裂等情况,分析了内饰板的结构特点,对其进行了工艺补充,并通过仿真实验验证了工艺补充的正确性。
2)通过DYNAFOEM软件研究了压边力、冲压速度、摩擦因数、拉延筋阻力占比4个参数对拉延成形减薄率的影响规律,并以此为基础确定了拉丁超立方抽样的区间。
3)建立了GA–BP神经网络模型,并通过遗传算法求得最优工艺参数及最优解如下:压边力为1 251.06 kN、冲压速度为6 209.20 mm/s、摩擦因数为0.06、拉延筋阻力占比为28.18%,此时拉延成形的最大减薄率为16.548%。将数据带入仿真软件DYNAFORM中得到的最大减薄率为16.167%,仿真误差与预测误差大小仅差0.318%,仿真误差精度为2.36%,说明了GA–BP神经网络模型的准确性。
4)GA–BP神经网络的样本数据如能在生产实际中获得,将提高此模型在实际生产中的预测精度。
[1] 郑辉, 车颖. 汽车发动机罩内板冲压成形分析[J]. 锻压装备与制造技术, 2011, 46(4): 68-70.
ZHENG Hui, CHE Ying. Analysis of Stamping Forming of Automobile Engine Hood Inner Plate[J]. Forging Equipment and Manufacturing Technology, 2011, 46(4): 68-70.
[2] 田永生, 邓国朝, 李梦瑶, 等. 基于Autoform-Sigma的汽车A柱内板冲压工艺参数优化[J]. 锻压技术, 2021, 46(3): 101-104.
TIAN Yong-sheng, DENG Guo-chao, LI Meng-yao, et al. Optimization of Stamping Process Parameters of Automobile A-Pillar Inner Plate Based on Autoform-Sigma[J]. Forging Technology, 2021, 46(3): 101-104.
[3] 陈小芳, 扶名福, 袁志军. DYNAFORM数值模拟技术在汽车覆盖件成形中的应用[J]. 热加工工艺, 2009, 38(11): 89-92.
CHEN Xiao-fang, FU Ming-fu, YUAN Zhi-jun. Application of DYNAFORM Numerical Simulation Technology in Automobile Panel Forming[J]. Hot Working Technology, 2009, 38(11): 89-92.
[4] 孙慧, 贾娟娟. 基于Dynaform软件和正交试验相结合的拉深工艺参数优化[J]. 锻压技术, 2016, 41(3): 148-152.
SUN Hui, JIA Juan-juan. Optimization of Drawing Process Parameters Based on the Combination of Dynaform Software and Orthogonal Experiment[J]. Forging & Stamping Technology, 2016, 41(3): 148-152.
[5] 徐小娟, 穆瑞. 基于正交试验的铝合金板料自冲铆接成形参数优化[J]. 锻压技术, 2019, 44(9): 51-55.
XU Xiao-juan, MU Rui. Optimization of Aluminum Alloy Sheet Self-Piercing Riveting Forming Parameters Based on Orthogonal Experiments[J]. Forging Technology, 2019, 44(9): 51-55.
[6] 臧其其, 闫华军, 张双杰. 基于Dynaform的铝合金汽车地板梁成形分析及工艺参数优化[J]. 塑性工程学报, 2019, 26(2): 125-131.
ZANG Qi-qi, YAN Hua-jun, ZHANG Shuang-jie. Dynaform-Based Forming Analysis and Process Parameter Optimization of Aluminum Alloy Automotive Floor Beams[J]. Journal of Plasticity Engineering, 2019, 26(2): 125-131.
[7] 王康康, 陈泽中, 江楠森, 等. 基于GA-BP的汽车行李箱盖内板冲压成形工艺优化[J]. 塑性工程学报, 2021, 28(9): 28-34.
WANG Kang-kang, CHEN Ze-zhong, JIANG Nan-sen, et al. Optimization of Stamping Forming Process for the Inner Panel of Automobile Trunk Lid Based on GA-BP[J]. Chinese Journal of Plasticity Engineering, 2021, 28(9): 28-34.
[8] 刘强, 俞国燕, 梅端. 基于Dynaform与RBF-NSGA-Ⅱ算法的冲压成形工艺参数多目标优化[J]. 塑性工程学报, 2020, 27(3): 16-25.
LIU Qiang, YU Guo-yan, MEI Duan. Multi-Objective Optimization of Stamping Process Parameters Based on Dynaform and RBF-NSGA-Ⅱ Algorithm[J]. Chinese Journal of Plasticity Engineering, 2020, 27(3): 16-25.
[9] ZHANG D H, BAI D P, LIU J B et al. Formability Behaviors of 2A12 Thin-Wall Part Based on DYNAFORM and Stamping Experiment[J]. Composites Part B, 2013, 55: 591-598.
[10] 崔学习, 万敏, 吴向东, 等. 基于电磁辅助成形的汽车覆盖件成形工艺研究[J]. 精密成形工程, 2021, 13(5): 66-71.
CUI Xue-xi, WAN Min, WU Xiang-dong, et al. Research on the Forming Process of Automobile Panels Based on Electromagnetic Assisted Forming[J]. Journal of Netshape Forming Engineering, 2021, 13(5): 66-71.
[11] MA G Y, HUANG B B, PERERA R. Optimization of Process Parameters of Stamping Forming of the Automotive Lower Floor Board[J]. Journal of Applied MathematicsVolume, 2014: 1-9.
[12] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005: 30-40.
BAI Jin-ze. LS-DYNA3D Theoretical Basis and Case Analysis[M]. Beijing: Science Press, 2005: 30-40.
[13] 管艳杰. 汽车覆盖件冲压成形工艺数值模拟及优化[D]. 太原: 太原科技大学, 2012: 20-25.
GUAN Yan-jie. Numerical Simulation and Optimization of Stamping Process for Automobile Panels[D]. Taiyuan: Taiyuan University of Science and Technology, 2012: 20-25.
[14] 王开阳. 基于CAE的汽车下横梁成形工艺优化[D]. 芜湖: 安徽工程大学, 2019: 25-27.
WANG Kai-yang. Forming Process Optimization of Automobile Lower Beam Based on CAE[D]. Wuhu: Anhui University of Technology, 2019: 25-27.
[15] 熊文韬. 基于GS理论与神经网络的汽车覆盖件成形优化[D]. 昆明: 昆明理工大学, 2017: 52-54.
XIONG Wen-tao. Forming Optimization of Automobile Panels Based on GS Theory and Neural Network[D]. Kunming: Kunming University of Science and Technology, 2017: 52-54.
[16] 郭强, 郑燕萍, 朱伟庆, 等. 基于BP神经网络遗传算法的高强钢成形研究[J]. 材料科学与工艺, 2020, 28(2): 89-96.
GUO Qiang, ZHENG Yan-ping, ZHU Wei-qing, et al. Research on High Strength Steel Forming Based on BP Neural Network Genetic Algorithm[J]. Materials Science and Technology, 2020, 28(2): 89-96.
[17] 陈靖芯, 蔡兰, 陆国民. 基于BP神经网络的车身钣金件冲压成形回弹预测[J]. 农业机械学报, 2005(7): 135-139.
CHEN Jing-xin, CAI Lan, LU Guo-min. Prediction of Springback of Body Sheet Metal Stamping Based on BP Neural Network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005(7): 135-139.
[18] 白雪, 胡建华, 樊浩森, 等. 汽车后围板拉深成形过程中的回弹预测[J]. 锻压技术, 2017, 42(9): 42-46.
BAI Xue, HU Jian-hua, FAN Hao-sen, et al. Springback Prediction during Deep Forming of Automobile Rear Wall Plate[J]. Forging Technology, 2017, 42(9): 42-46.
[19] 李奇涵, 王红强, 刘海静, 等. 基于BP神经网络矩形盒件拉深成形变压边力的预测[J]. 锻压技术, 2015, 40(11): 27-31.
LI Qi-han, WANG Hong-qiang, LIU Hai-jing, et al. Prediction of Variable Blank Holder Force in Deep Drawing of Rectangular Box Based on BP Neural Network[J]. Forging & Stamping Technology, 2015, 40(11): 27-31.
[20] 李丹. 基于改进遗传算法的柔性作业车间调度问题的研究[D]. 昆明: 昆明理工大学, 2021: 21-22.
LI Dan. Research on Flexible Job Shop Scheduling Problem Based on Improved Genetic Algorithm[D]. Kunming: Kunming University of Science and Technology, 2021: 21-22.
[21] 郭强, 郑燕萍, 朱伟庆, 等. DP-780高强钢车身侧围板成形质量优化[J]. 塑性工程学报, 2019, 26(1): 40-45.
GUO Qiang, ZHENG Yan-ping, ZHU Wei-qing, et al. Quality Optimization of Forming Side Panel of DP-780 High-Strength Steel Body[J]. Chinese Journal of Plastic Engineering, 2019, 26(1): 40-45.
[22] 孙元贵. 基于响应面与遗传算法的汽车底板成形优化[D]. 昆明: 昆明理工大学, 2018: 56-59.
SUN Yuan-gui. Optimization of Automotive Floor Forming Based on Response Surface and Genetic Algorithm[D]. Kunming: Kunming University of Science and Technology, 2018: 56-59.
[23] 邱小婷, 赵伟, 滕培秀, 等. 基于神经网络与遗传算法的方锥件渐进成形扭曲位移优化[J]. 模具工业, 2017, 43(12): 1-5.
QIU Xiao-ting, ZHAO Wei, TENG Pei-xiu, et al. Progressive Forming of Square Cones Based on Neural Network and Genetic Algorithm for Distortion Displacement Optimization[J]. Mould Industry, 2017, 43(12): 1-5.
[24] MATLAB技术论坛. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013: 34-41.
MATLAB Technology Forum. Analysis of 43 Cases of MATLAB Neural Network[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2013: 34-41.
Virtual Manufacturing of Automotive Interior Trim Panels Based on GA-BP Neural Network
ZHANG De-hai,FU Liang,LI Yan-qin,LI Jun-heng,ZHU Zhi-feng,HUANG Zi-fan
(School of Mechanical and Electrical Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China)
The work aims to conduct virtual manufacturing with automotive interior panel as the research object to obtain relatively accurate process parameters in advance and reduce the occurrence of forming defects. Firstly, the effects of process parameters on the quality of product drawing was studied, and the Latin hypercube sampling interval was determined; secondly, 60 sets of sample data were drawn in the sampling interval, and the maximum thinning rate was used as the target value, the first 50 sets of sample data were used as the test set and the last 10 sets of sample data were taken as expected set. Genetic algorithm based on GA-BP neural network was used to obtain the optimal process parameters, which were substituted into DYNAFORM for virtual manufacturing. After training, the maximum error between the test value and the expected value of the GA-BP model was 0.299 7%, and the maximum prediction error rate was 1.747 38%; the maximum thinning rate predicted by the genetic algorithm was 16.548%, and the thinning rate obtained by virtual manufacturing was 16.167%. The difference between the virtual manufacturing value and the predicted value was only 0.318%, and the error rate of the simulation error was 2.36%. The optimization method of virtual manufacturing combined with advanced algorithms can guide subsequent production.
DYNAFORM; GA-BP neural network; interior panel
10.3969/j.issn.1674-6457.2022.09.006
TG302;TG386.3
A
1674-6457(2022)09-0041-09
2021–11–13
江苏省盐城市“515”创新领军人才项目(盐委[2020]40号);河南省科技攻关项目(202102210087);郑州市科技局产学研项目(郑科函[2020]3号)
张德海(1973—),男,博士,教授,主要研究方向为先进材料成形过程控制、三维光学检测及其交叉学科。
责任编辑:蒋红晨

