高钢级管道延性断裂过程中壁厚减薄率研究*
崔富凯, 甄 莹
(中国石油大学(华东), 山东 青岛 266580)
0 前 言
“一带一路” 战略中有关于天然气长输管线的国家能源顶层设计与民众持续迅猛增长的天然气需求, 推动长输管道行业迎来了新一轮的发展高峰[1-2], 采用高钢级、 大直径管道进行高压输送已成为管道工程发展的必然趋势[3-4]。 高钢级管材韧性好、 强度高, 但在其生产及运输过程中仍不可避免的会形成各类缺陷及机械损伤, 上述裂纹源在管道内高压气体驱动下会迅速扩展, 并造成数百米甚至上千米的管道破坏, 极易引发严重的安全问题, 甚至导致灾难性后果[5-9]。 因此, 明确并控制管道断裂行为便成为了管线建设和安全运行的重要课题, 管壁减薄作为高钢级管道延性断裂过程中的典型行为也受到越来越多的关注。
全尺寸气体爆破试验是世界公认的研究管道断裂行为最为有效的方法[10], 但是该试验难度大、 周期长、 成本高, 而且难以在试验过程中监测壁厚减薄率这一参量。 数值模拟方法可有效实现高钢级管道延性裂纹动态扩展的模拟, 有望成为研究管道壁厚减薄行为的有效手段。 吕锦杰等[11-12]使用CZM (内聚力模型) 对X80 管道裂纹动态断裂过程进行了模拟; Liu 等[13]利用XFEM (扩展有限元) 基于三维实体单元对压力容器的塑性失效及裂纹扩展行为进行了研究;Nonn[14]利用Gurson-Tvergaard-Needleman(GTN)模型对高钢级管道的韧性裂纹扩展进行了模拟; Oikonomidis[15]基于SDRR (考虑应变率的损伤模型) 对长程管道裂纹扩展问题开展了相关研究。
通过对比上述裂纹动态扩展模拟方法及模拟结果, 发现GTN 模型具有精度高且可反映管道真实约束状态的优点。 因此, 本研究以X80 管道为例, 采用GTN 模型对其延性裂纹动态扩展过程进行模拟, 在验证模型可靠性的基础上, 研究管道壁厚减薄情况, 分析管壁减薄发生的区域及壁厚减薄率沿管道轴向的变化趋势。 通过模拟不同内压、 不同管道壁厚与直径、 不同回填深度及不同钢级管道的延性裂纹动态扩展过程, 分析设计系数、 管道几何尺寸、 回填效应及管材特性对管道壁厚减薄分布规律及数值大小的影响, 以得到相应规律, 并为高钢级管道断裂机理及止裂控制研究提供依据。
1 X80 管道有限元模型
本研究所用X80 管道外径为1 422 mm, 壁厚为27.7 mm, 考虑管道在轴向和径向方向结构和载荷的对称性, 借助Hypermesh 软件建立其四分之一模型, 引入与管道外径尺寸相同的初始裂纹, 为保证裂纹可以充分扩展, 将管道轴向总长的一半设为6 倍外径, 并在模型裂纹前端设置一定宽度的孔洞损伤断裂过程区。 GTN 模型具有严重的网格依赖性, 将损伤断裂过程区管壁厚度方向划分12 层单元, 单元高度设为0.25 mm,采用过渡网格技术对管道网格进行划分以实现单元密度沿轴向及环向的逐渐递减, 以此缩短计算时间。 利用GTN 模型成功分析塑性损伤的关键是正确识别其9 个损伤参数, 笔者已在之前的工作中对X80 管道钢本构及损伤参数进行了标定[16], 将标定的GTN 损伤演化参数赋予断裂过程区, 其余位置设置传统弹塑性材料参数。 全尺寸管道有限元模型如图1 所示。
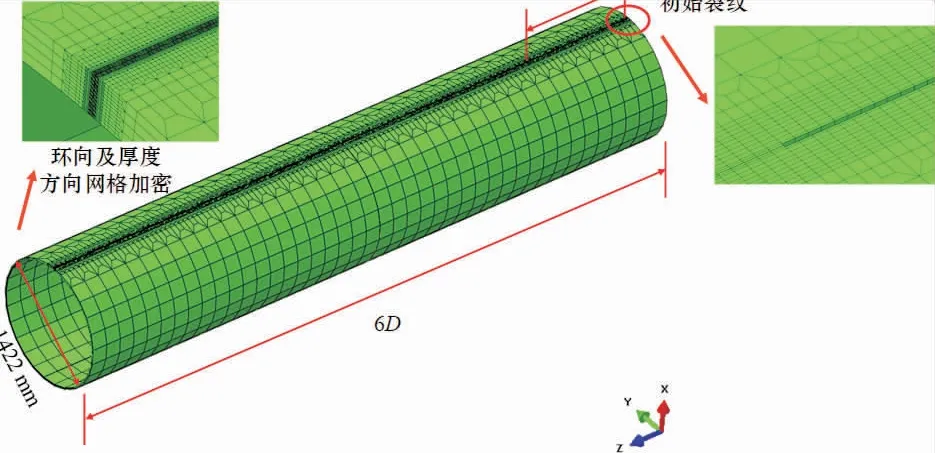
图1 全尺寸管道有限元模型
除了选用合适的延性损伤模拟技术描述动态断裂外, 管道裂纹动态扩展模拟中最大的难点在于复杂加载的实现。 本研究不考虑气体与管道结构变形之间的流固耦合过程, 而是采用基于全尺寸爆破试验数据简化的压力衰减模型对管道气体减压过程进行近似模拟。 该方法需要将管道以裂纹尖端为界, 将其划分为前后两个不同的加载区[17-18]。 裂纹尖端前的区域认为是压力均匀分布且始终等于裂尖压力, 裂纹尖端后的压力Pb衰减趋势可以近似为以下指数型函数

式中: P0——裂纹尖端初始压力;
z——裂纹尖端后面的轴向坐标;
D——管道外径。
根据Nonn 等[14]提供的管道全尺寸爆破试验数据, 设定初始压力为18.7 MPa。 加载过程中设置初始内压随计算时间线性下降, 当Δt=20 ms 时,下降至初始水平P0的40%。 上述加载过程均通过用户子程序VDLOAD 在Abaqus/Explicit 求解器中实现。
2 X80 管道有限元模拟结果
图2 所示为有限元模拟裂纹扩展速度随时间的变化规律, 与文献[14]中提供的试验数据吻合较好, 可以认为所建立的有限元模型可靠。
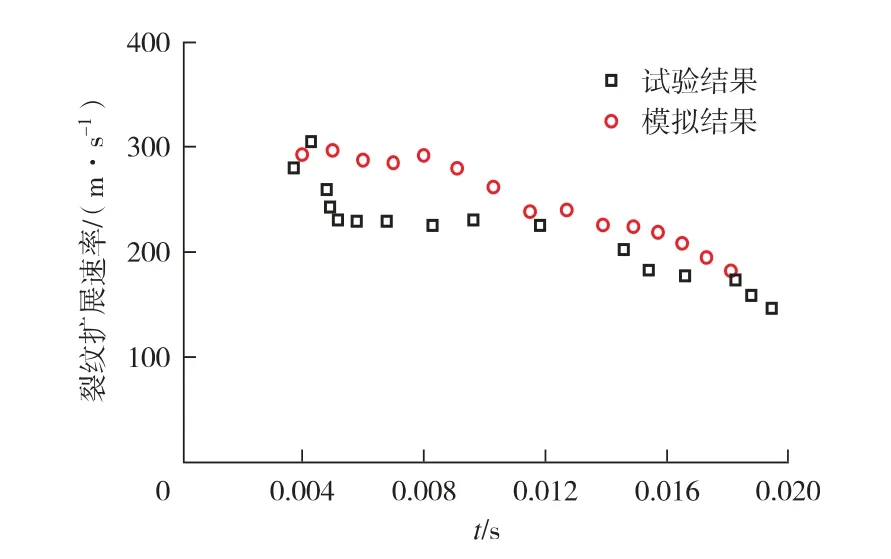
图2 试验与模拟所得裂纹扩展速度对比
图3 所示为裂纹扩展至一定长度时管道的整体变形和等效应变分布情况。 从图3 中可以看出, 管道在内部气压作用下明显张开, 塑性变形主要集中于裂纹张开的襟翼上。

图3 管道整体变形及等效塑性应变分布云图
管道轴向的断面形貌如图4 所示, 从图4中可以看出, 管道裂纹扩展过程中其裂纹前沿趋于拱形, 说明其壁厚中间部分约束程度最高, 对塑性变形的限制最大, 因此壁厚中间裂纹更易起裂及扩展。 同时, 由于管道同时受到径向压缩、 环向拉伸及轴向拉伸的共同作用,管道裂纹尖端附近出现了颈缩, 即壁厚减薄的情况。
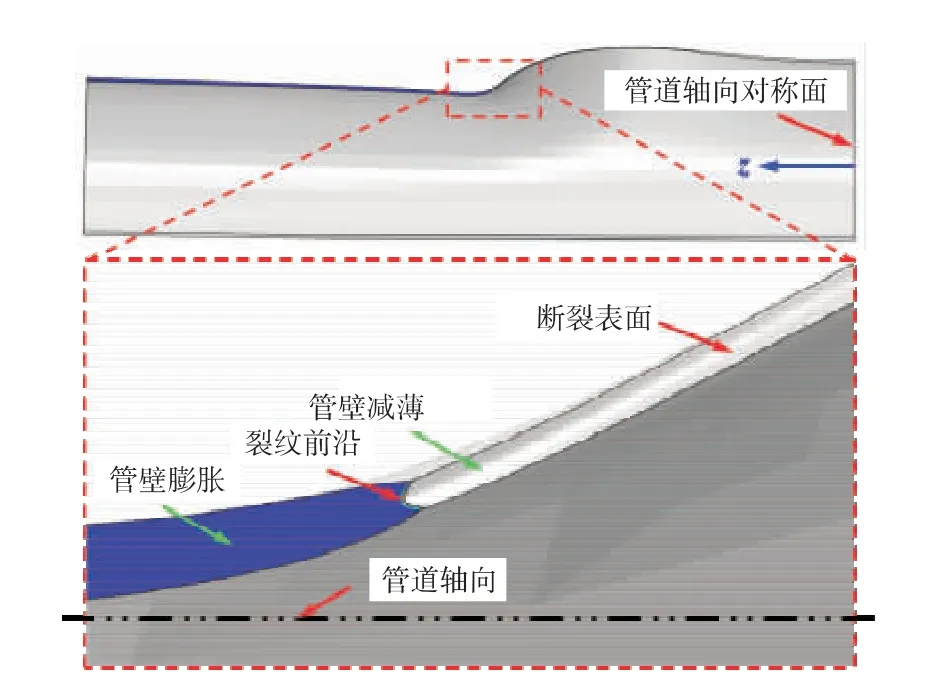
图4 管道轴向断面形貌
分别提取管道设计系数DF 为0.80、 0.72及0.56 的工况下, 裂纹扩展长度Δa 分别为0.2D、 1.0D、 2.0D、 3.0D 时壁厚减薄率沿管道轴向的分布情况, 如图5 所示, 图5 中z 为取值位置距管道轴向对称面的轴向距离 (如图4所示)。 从图5 中可以看出, 设计系数对壁厚减薄率沿轴向分布规律及范围并无影响, 管壁颈缩均主要集中于管道初始裂纹尖端至当前裂纹尖端的范围内, 因此, 其范围会随裂纹扩展而不断增大, 从数值上看, 壁厚减薄率均由初始裂纹尖端处的0 值迅速上升, 达到一较大数值之后再以较缓的速度增加, 在当前裂纹尖端附近达到最大值。
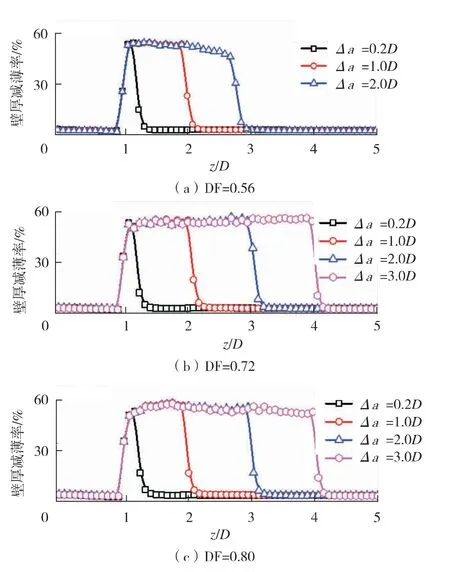
图5 不同设计系数下壁厚减薄率沿管道轴向分布规律
进一步提取了不同设计系数下管道裂纹尖端处壁厚减薄率 (即最大壁厚减薄率) 随裂纹扩展长度的变化, 如图6 所示。 从图6 中可以看出, 对于某一特定工况, 尽管裂纹扩展中压力不断衰减, 但壁厚减薄率最大值均保持在50%左右, 当设计系数≥0.56 时, 设计系数对裂纹扩展过程中壁厚减薄率最大值几乎没有影响; 而当设计系数为0.43 时, 管道裂纹未能达到稳定扩展阶段, 其壁厚减薄率也较小。 可以认为, 设计系数对管道壁厚减薄率最大值也无影响。

图6 不同设计系数下管道壁厚减薄率随裂纹扩展长度的变化
3 管道壁厚减薄率影响因素研究
首先探究设计系数为0.72、 外径为1 422 mm时, 径厚比分别为51.3、 66.4 及103 的X80 管道壁厚对壁厚减薄率的影响。 不同壁厚管道在特定裂纹扩展长度下对壁厚减薄率的影响如图7所示, 从图7 中可以看出, 管道壁厚的变化对壁厚减薄率分布规律、 管壁颈缩及膨胀区范围均无影响。

图7 管道壁厚对壁厚减薄率分布规律的影响
进一步提取不同壁厚管道裂纹尖端位置管壁减薄率随裂纹扩展长度的演化规律, 如图8所示。 从图8 中可以看出, 管道壁厚越小, 壁厚减薄率越大, 径厚比为51.3、 66.4 及103 的管道对应的最大壁厚减薄率平均值分别为50%、 55.41%、 57%。 结合图7 可以看出, 管道壁厚越小, 其膨胀率绝对值也越小, 因此为保证管道体积不变, 可以推测出相较于大壁厚管道,小壁厚管道的管壁发生环向减薄的范围也更大。

图8 管道壁厚对壁厚减薄率演化规律的影响
本研究的对象为大直径管道, 因此以设计系数为0.72、 径厚比为66.4, 直径分别为1 422 mm、1 219 mm、 1 016 mm 及914.4 mm 的X80 管道为例, 探究直径变化对天然气管道壁厚减薄率的影响。 管道直径对壁厚减薄率分布规律的影响如图9 所示, 从图9 中可以看出, 对于不同直径的管道, 管壁颈缩区以初始裂纹尖端与当前裂纹尖端之间的范围为主, 而管壁膨胀区则限制在初始裂纹尖端后的区域。 因此, 颈缩区范围仍然保持了随裂纹扩展逐渐扩大但最大壁厚减薄率不变的趋势; 膨胀区仍然保持了随裂纹扩展其范围不变但最大壁厚减薄率绝对值逐渐增大的趋势。

图9 管道直径对壁厚减薄率分布规律的影响
提取不同直径管道的裂纹尖端处管道壁厚减薄率随裂纹扩展演化规律, 如图10 所示。 从图10中可以看出, 对于具有相同径厚比的不同直径的管道, 其壁厚减薄率随裂纹扩展演化规律一致, 直径1 422 mm、 1 219 mm、 1 016 mm 及914.4 mm 的管道对应的裂尖壁厚减薄率分别为55.41%、 55.48%、56.94%与57.24%, 可见随管道直径减小, 最大壁厚减薄率略微呈现增加趋势, 但整体数值差别较小, 可以认为直径对壁厚减薄率无影响。
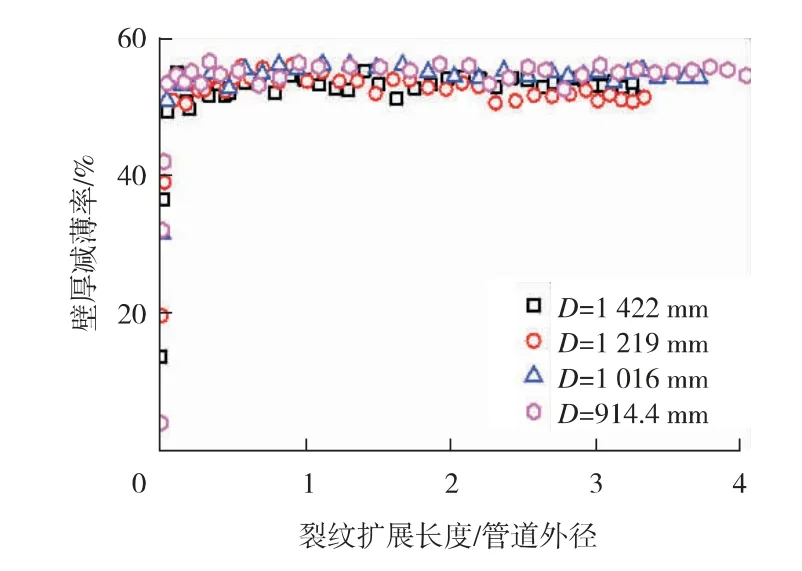
图10 管道直径对壁厚减薄率演化规律的影响
为研究管材特性对天然气管道壁厚减薄行为的影响, 在前文X80 管道相关研究的基础上,另外选取X100[19]、 X65[20]管道对直径1 422 mm、壁厚27.7 mm 的管道裂纹扩展进行分析, 三种管道真实应力-应变曲线如图11 所示。 根据管材的屈服强度对不同钢级管道设置不同内压水平,保证各管道设计系数均为0.72。
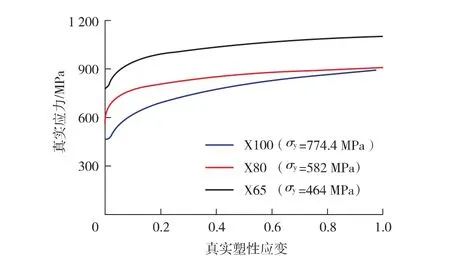
图11 不同钢级管道真实应力-应变曲线
图12 所示为管道强度对壁厚减薄率分布规律的影响, 图13 所示为管道强度对壁厚减薄率演化规律的影响。 从图12 中可以看出,管道强度对壁厚减薄率分布规律、 分布范围几乎没有影响, 而图13 表明其对裂纹扩展过程中裂纹尖端处壁厚减薄率即壁厚减薄率最大值有一定影响, X100、 X80、 X65 管道对应的裂纹尖端处壁厚减薄率平均值分别为48.32%、50%与52.29%。 由以上试验结果可见, 管道的强度越小, 其壁厚减薄率就越大, 这也从壁厚减薄的角度进一步说明了采用高钢级管道的必要性。

图12 管道强度对壁厚减薄率分布规律的影响

图13 管道强度对壁厚减薄率演化规律的影响
4 结 论
(1) 管道壁厚减薄发生在初始裂纹尖端至当前裂纹尖端的范围内, 该范围随裂纹的扩展不断扩大, 但管壁减薄率最大值始终出现在裂纹尖端处, 且不随裂纹扩展变化。 设计系数、 管道几何尺寸及管材特性对壁厚减薄范围均无影响。
(2) 当管道设计系数由0.56 增大至0.8 时,管道壁厚减薄率的最大值基本不变; 壁厚越小,其减薄现象越明显, 直径为1 422 mm、 径厚比分别为51.3、 66.4 及103 的管道最大壁厚减薄率平均值分别为50%、 55.41%、 57%; 直径变化对管道壁厚减薄率影响较小, 径厚比为66.4、 直径分 别 为1 422 mm、 1 219 mm、 1 016 mm 及914.4 mm 的管道最大壁厚减薄率分别为55.41%、 55.48%、 56.94%与57.24%; 管道钢级越高, 最大壁厚减薄率越小, X100、 X80、 X65管道对应的裂纹尖端处壁厚减薄率平均值分别为48.32%、 50%与52.29%。

