基于有限元不同大塑性变形应变特征对比研究及组织分析

胡晴航，田文春，李萍

基于有限元不同大塑性变形应变特征对比研究及组织分析

胡晴航，田文春，李萍

（合肥工业大学 材料科学与工程学院，合肥 230009）

探究往复挤压工艺（CEC）与往复挤扭镦工艺（SETE）的变形特点，并研究单道次变形后的金属流动行为和应变分布特征。以低活化钢为材料，对CEC和SETE等2种工艺下的变形过程进行有限元模拟分析，获得3个道次变形后的CLAM钢等效应变云图，同时，开展相关试验以验证有限元模拟的准确性。往复挤压工艺（CEC）与往复挤扭镦工艺（SETE）均能实现多道次累积应变，其中SETE下的单道次累积应变量更大，其各道次等效应变分别比CEC下的等效应变高2.47、5.06、7.84。0.5道次变形后，SETE下的平均硬度值比CEC下的高6.1HV。在CEC与SETE下进行各道次变形后，边缘等效应变都高于心部等效应变，且1道次变形后应变均匀性相差不大，但随着道次的增加，SETE下的应变分布更加均匀。0.5道次变形后，CEC与SETE下的边缘晶粒尺寸均较心部晶粒尺寸细小，且SETE下的晶粒细化程度更高。

应变分布特征；有限元模拟；变形行为；大塑性变形

随着现代工业的迅速发展，对高性能金属材料的需求日益增加，制备具有优异性能的材料一直是各国材料科学与工程领域研究的热点。就目前各国的研究现状来看，晶粒细化是实现金属材料优异性能的重要途径之一[1]。采用传统的锻造、挤压、轧制以及随后的再结晶退火处理工艺，尽管可以使晶粒尺寸最小达到10 μm，但仍难以满足对高性能材料的要求。大塑性变形就是在这样的背景下发展起来的一种用于提高材料性能的工艺技术[2]。

在20世纪四五十年代，Bridgeman最早奠定了大塑性变形技术（severe plastic deformation，SPD）的基础，使人们对高压和剧烈变形状态下的金属材料行为有了初步认识[3]。SPD的思路是选择恰当的塑性变形工艺，使材料在变形后保持与变形前一致的尺寸，材料可以以相同的工艺进行反复变形进而获得较大的累积应变量[4-5]。基于上述条件开发出了往复挤压工艺（cyclic extrusion compression，CEC），在CEC变形过程中，材料始终处于三向压应力状态，不会出现裂纹等缺陷，且可以进行多道次累积应变，该工艺被成功地用于生产各种具有超细晶结构的金属材料中[6-8]。挤扭工艺是一种具有代表性的塑性变形工艺，该工艺的原理如下：在其变形过程中，通过沿试样横截面某一方向扭转一定角度，从而产生剧烈的塑性变形[9-11]。将往复挤压变形与挤扭工艺结合，使扭转变形叠加到挤压变形中[12]，从而拓展出了往复挤扭镦工艺（sequential extrusion-twist-extrusion，SETE）。

CEC与SETE的原理如图1所示。文中采用有限元模拟和物理试验相结合的方法，对比研究了2种工艺变形过程中的金属流动行为、应变分布特征及微观组织演变情况，以期为制备力学性能更优的超细晶材料研究提供理论基础和依据。

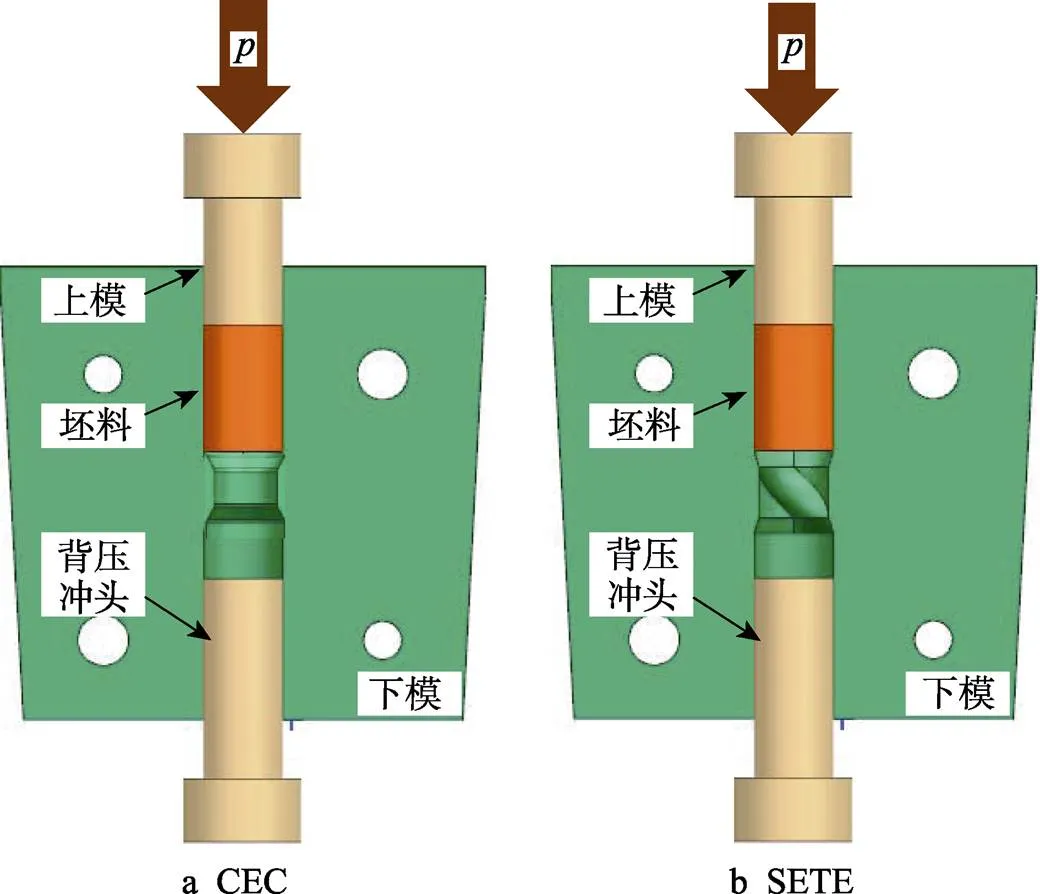
图1 工艺原理示意图

1 有限元模拟及试验

1.1 有限元模拟

采用三维建模软件UG对2种工艺的模具和坯料进行建模，后将建立的模型导入有限元模拟软件Deform–3D中。CEC与SETE变形所用坯料尺寸为24 mm×40 mm，材料选择低活化马氏体钢[13]，选用四面体进行网格划分，模具材料选用H13钢，上模速度为1 mm/s，摩擦因数设定为0.25，摩擦类型选用剪切摩擦。

1.2 材料与方法

试验材料为中国低活化马氏体钢，其主要成分（质量分数）如下：Cr为8.93%，W为1.51%，Mn为0.49%，V为0.15%，Ta为0.15%，C为0.091%，Si为0.05%，余量为Fe。该材料经“电阻炉熔炼—电渣重熔—热轧”后获得，采用电火花线切割机切取坯料。模具在线圈中加热至450 ℃，坯料于井式炉中加热至600 ℃，采用型号为YDZFEM–630T的压力机完成试验。

2 结果与分析

2.1 往复挤压变形过程分析

图2为0.5道次往复挤压变形各阶段应变分布云图。坯料随着上冲头下行开始向下流动，其下端流入缩颈区时被挤压（类似于普通的正挤压），随后，当材料流出缩颈区与镦粗段的过渡区（区）时，试样下端会受到背压冲头的作用开始出现镦粗变形，最后上冲头下行至下限位，坯料镦粗完毕后填满型腔。至此，0.5道次完成。随后将模具倒置，此时背压冲头作为主冲头，按照同样步骤完成另外的0.5道次变形。至此，完成了往复挤压的1道次变形。

在镦粗段某一横截面中心和外缘区域进行点追踪，图3为点追踪应变变化规律。可将其分为4个阶段：挤压变形阶段，此时材料刚进入缩颈区，应变迅速上升，且外缘区域的应变上升更快；稳定态1阶段，此时目标点完全进入缩颈区，处于稳定挤压态，其应变保持平缓；镦粗变形阶段，在背压冲头的作用下应变再次上升，且上升幅度几乎一致；稳定态2阶段，材料经过镦粗变形后进入稳定态，应变再次趋于平缓。最终，外缘处等效应变高于心部应变，其主要原因是挤压变形过程中外缘处累积应变要显著高于心部应变。

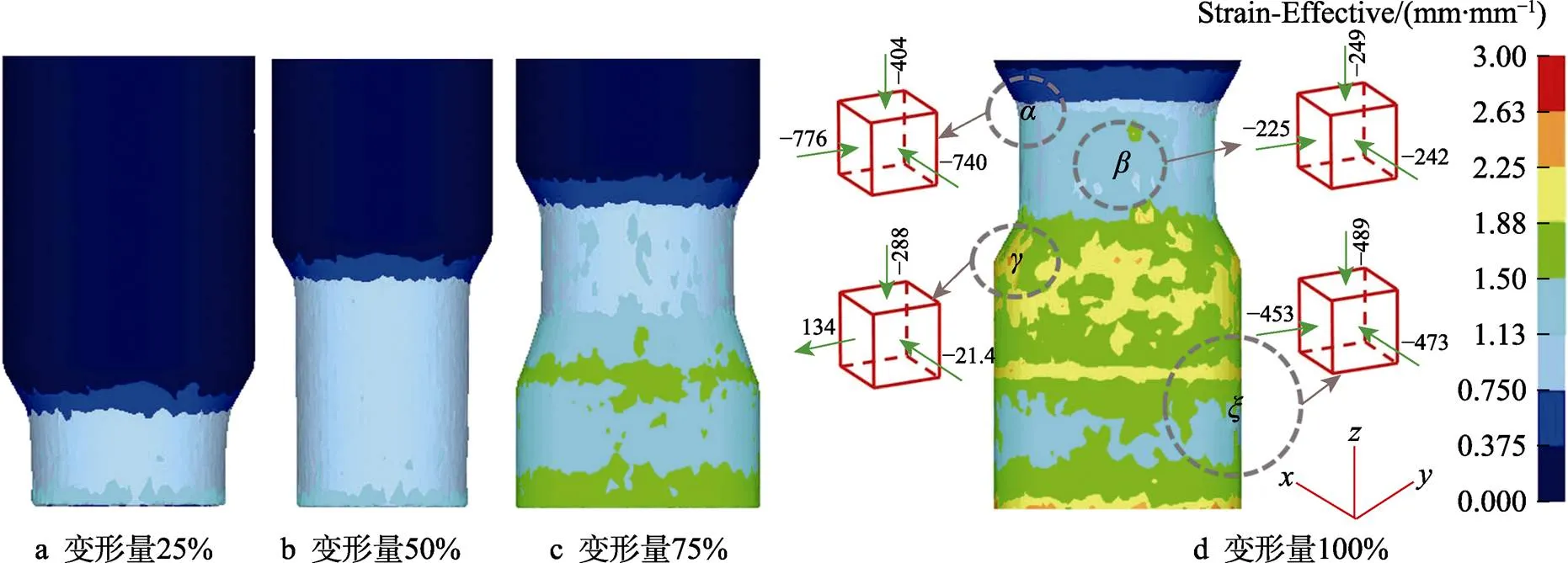
图2 0.5道次往复挤压变形各阶段应变分布云图

注：表示缩颈区外缘，三向压应力；表示缩颈区中心，三向压应力；表示过渡区，两向受压一向受拉；表示镦粗段，三向压应力。

图3 往复挤压变形点追踪应变变化规律

图4为0.5道次往复挤压终态应变分布云图。可以看到，等效应变沿外缘部分向中心逐渐降低，这是由于在变形过程中，外缘材料与缩颈处的模具侧壁之间存在较大摩擦，其流动速度存在速度差，应变累积更大，镦粗变形后使坯料横截面应变分布呈圆环状（如图4a所示）。由图4b可知，、截面径向应变曲线几乎重合，说明在镦粗段远离背压冲头的区域，其轴向应变变化不大，而截面等效应变相对较低，这是由于金属越靠近背压冲头，受到的摩擦作用越大，导致出现困难变形区，应变累积程度相对其他位置较低。

图4 0.5道次往复挤压终态应变分布云图

图5为往复挤压3个道次后纵截面应变分布云图，它同时表征了3个道次中应变分布特征的一致性和随着道次增加应变的变化情况。其中虚线左侧为3个道次在同一应变标尺下的应变分布情况，可见，随着道次的增加，应变不断累积；右侧为应变标尺阈值随着道次增加而增大后的应变分布情况，可以看出3个道次的应变分布特征几乎一致，只存在应变累积大小的差别。因此主要对1道次变形结果进行分析，其中I区金属是由0.5道次变形后的镦粗段外缘部分再次经历挤压+镦粗变形后形成的，其累积应变最大、变形程度最高。Ⅱ区来源于0.5道次变形后的缩颈区，Ⅱ区与缩颈区在各自道次中都属于小变形区，且靠近冲头，变形较为困难，累积应变最小。Ⅲ区是镦粗段靠近背压冲头的区域经历挤压变形得来的，累积应变较小。Ⅳ区是镦粗段中心再次经历轻微剪切变形和镦粗变形得来的，累积应变较大。

图5 往复挤压3个道次后纵截面应变分布云图

2.2 往复挤扭镦变形过程分析

图6为往复挤扭镦0.5道次各阶段应变分布云图。坯料随着上冲头的下行首先发生挤压变形进入扭转通道，随后在通道中发生扭转剪切变形。当坯料被挤出扭转通道时，在背压冲头的作用下发生镦粗变形，应变进一步累积，直到上冲头下行至下限位，0.5道次完成。随后将模具倒置，此时背压冲头作为主冲头，按照同样的步骤完成另外的0.5道次变形，至此，完成了往复挤扭镦的1道次变形。

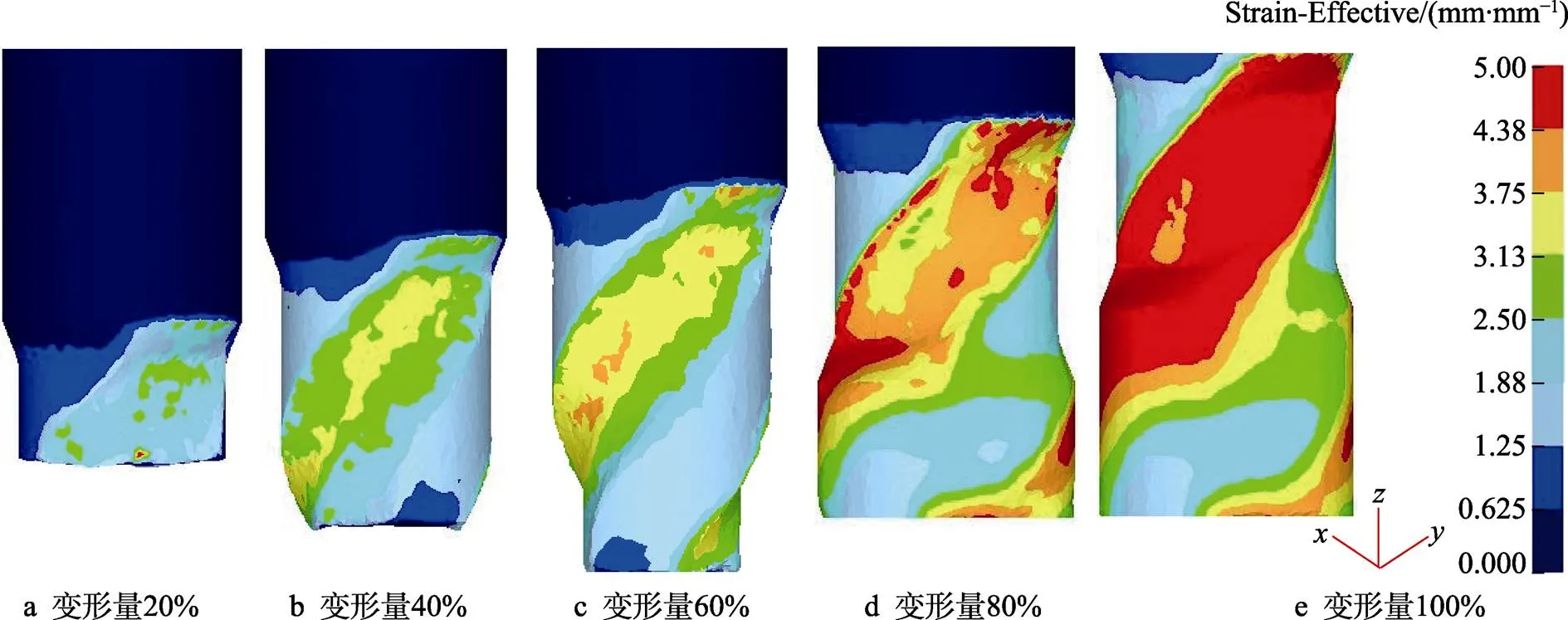
图6 往复挤扭镦0.5道次各阶段应变分布云图

在镦粗段某一横截面中心和外缘区域进行点追踪，图7为点追踪应变变化规律。可以看出，材料首先发生挤压变形，应变逐渐上升，目标点进入扭转通道后，中心区域几乎没有发生剪切变形，其应变变化趋势较为平缓，而外缘部分发生扭转剪切变形，应变不断上升。当材料被挤出扭转通道后，受到背压作用发生镦粗变形，应变再次出现累积，随着背压冲头施加的力达到最大值而保持恒定，各区域应变保持缓慢上升趋势。

图8为0.5道次往复挤扭镦终态应变分布云图。等效应变沿外缘部分向中心呈递减趋势，这是由于试样在经过扭转通道时发生了剪切变形，且距离中心越远的区域剪切作用越强烈，累积的变形量越大，最后经历镦粗变形后应变呈梯度式分布。由图8b可知，和截面的径向应变要大于截面的，这是由于金属越靠近背压冲头，受到摩擦力作用会越大，金属变形越加困难，应变累积减少。

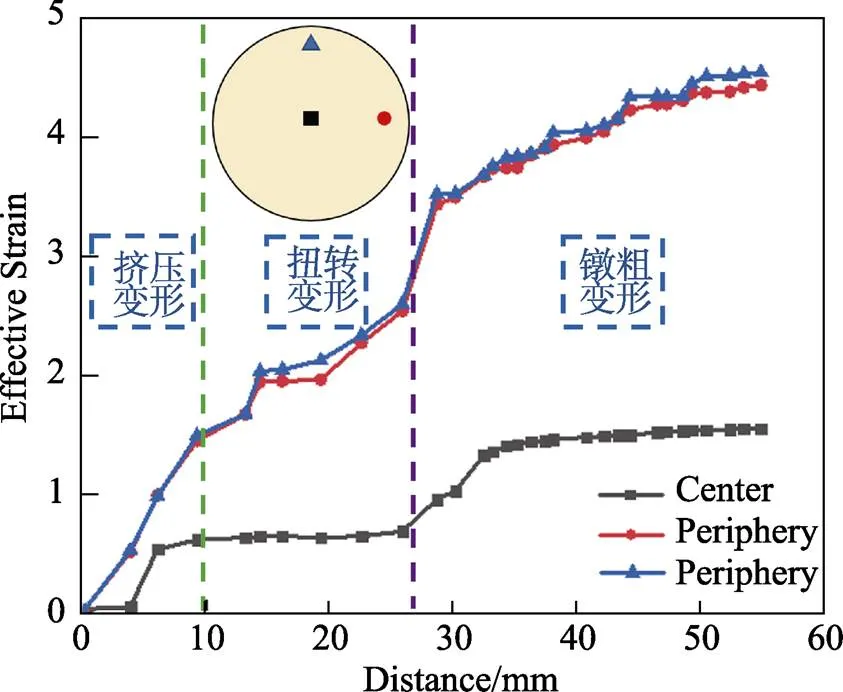
图7 往复挤扭镦变形点追踪应变变化规律

图8 0.5道次往复挤扭镦终态应变分布云图

图9为往复挤扭镦3个道次后纵截面应变分布云图。3个道次的应变分布特征几乎一致，只存在应变累积大小的差别，因此主要分析1道次变形过程，由于只改变了缩颈区形状，其变形轨迹与往复挤压变形轨迹类似。I区金属是由0.5道次变形后的镦粗段外缘部分经历了挤压+扭转+镦粗变形后形成的，其累积应变最大，变形程度最高。Ⅱ区来源于缩颈区，累积应变最小。Ⅲ区是镦粗段靠近背压冲头的区域经历挤压+扭转变形得来的，累积应变较小。Ⅳ区是镦粗段中心再次经历挤压+轻微扭转+镦粗变形得来的，累积应变较大。

图9 往复挤扭镦3个道次后纵截面应变分布云图

2.3 应变分布特征分析

为了探究2种工艺对试样应变分布均匀性的影响，引入非均匀性参数F[14]，该参数值越小，表示均匀性越高，其计算公式如式（1）所示。

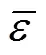
图10为CEC和SETE计算F值的纵截面选取位置，由于CEC变形后，应变沿中心轴呈对称分布，绕中心轴各截面的应变分布几乎一致，可用某一纵截面代替整体，因此选取图10a中截面。而SETE变形后，过中心轴的竖直截面应变分布不一致，且其扭转角度为90°，故选取图10b中¢、¢、¢、¢等4个纵截面，每个截面间隔45°，分别计算出各截面的F并取其平均值来反映SETE应变分布均匀性。

图10 纵截面位置

图11为所选截面各道次下的F变化趋势。可以看出，随着道次的增加，各截面的F减小。1道次变形后，CEC的F略低于SETE的，但随着多道次的进行，SETE的F下降得更快，其应变分布比CEC的更加均匀。截面¢与¢、截面¢与¢的F在各道次几乎一致，即SETE试样中相互垂直的任意截面的应变分布均匀性相同。

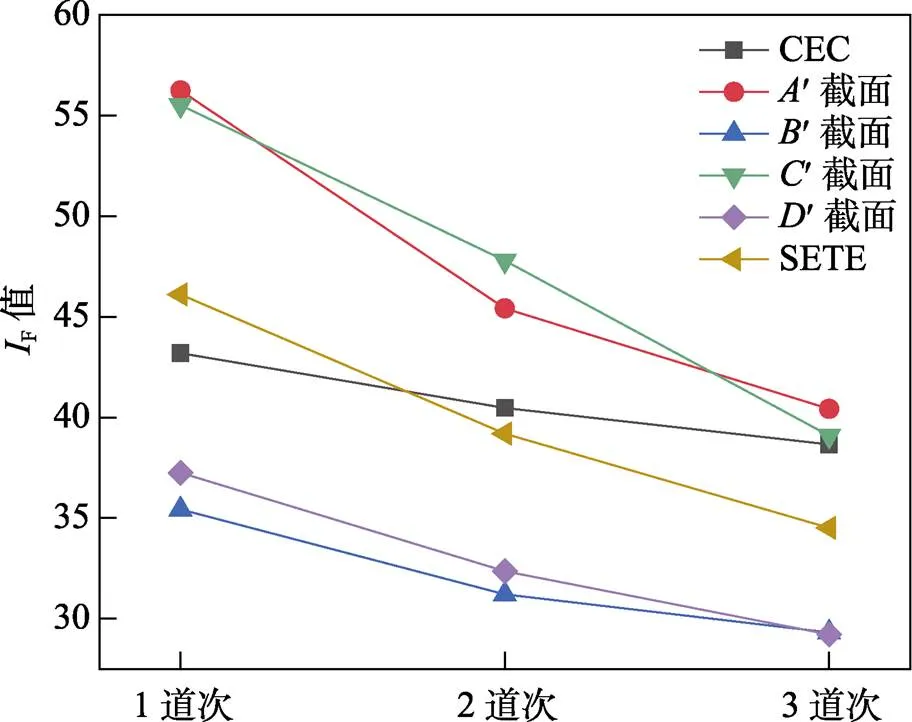
图11 各截面IF变化趋势

图12为2种工艺下各道次的等效应变值。可以看出，随着多道次的进行，两者的应变呈递增趋势，且SETE下各道次等效应变值分别比CEC下的应变大2.47、5.06、7.84，说明当缩颈区为挤扭通道时，材料在发生挤压变形的同时还受到扭转剪切变形，因此SETE较纯挤压变形能更好地累积应变。

图12 2种工艺下各道次等效应变变化趋势

3 试验验证

根据模拟结果可知，2种工艺下各道次的应变分布特征几乎一致，但多道次变形后，金属流动较为复杂，难以确定变形方式、变形历史对组织和性能的影响规律，因此0.5道次变形后的镦粗段更能体现2种工艺变形效果的区别。CEC变形后应变沿轴向变化不大，而SETE变形后应变呈梯度分布，为了反映总体微观组织的区别，可选取两者镦粗段中部的横截面（图4a中的截面）作为研究对象。在试样表面上以1.5 mm为间隔等距测量获得显微硬度，试验设备为MH–3显微硬度计，加载载荷为200 g，保压时间为15 s。

图13为变形前后的金相照片，图13a为明显的回火马氏体组织。SETE变形后，在剪切力的作用下，部分板条组织沿扭转方向被拉长，呈涡旋状分布，而心部应变量较小，且几乎未经历扭转变形，无晶粒拉长现象，其晶粒尺寸较边缘尺寸大。CEC变形后，其晶粒尺寸较初始态尺寸要小，但无SETE细化效果明显，且心部晶粒比边缘晶粒更为粗大。由图13b和13c可知，边缘应变高于心部应变，且单道次SETE对晶粒的细化效果要高于CEC的，该结论验证了有限元模拟的准确性。

图13 变形前后金相照片

图14为2种工艺变形后镦粗段中部横截面的硬度云图。CEC变形后，硬度呈圆环分布，且沿半径方向向外递增，而SETE变形后，硬度沿中心线呈对称分布，且越靠近外缘，硬度越高。SETE变形后的平均硬度值比CEC的高6.1HV，这是由于SETE变形累积的应变量较大，位错密度更高，试样产生了加工硬化[15]，硬度上升幅度大。2种工艺下变形后的硬度分布规律与模拟结果中的应变分布规律大致匹配，进一步验证了数值模拟与物理试验的准确性。

图14 横截面硬度云图

4 结论

1）CEC与SETE都能实现多道次变形累积应变，且各道次变形后，边缘等效应变都要高于心部应变，其中SETE下单道次累积应变量更大，各道次等效应变分别比CEC下的应变大2.47、5.06、7.84。

2）1道次变形后，CEC与SETE下的应变均匀性相差不大，但随着道次的增加，SETE下的应变分布更加均匀。SETE下相互垂直截面的F变化趋势几乎一致，应变分布均匀性相同。

3）0.5道次变形后，CEC与SETE下的边缘晶粒尺寸较心部尺寸细小，且SETE的细化程度更高。CEC变形后硬度呈圆环状分布，且沿半径方向向外递增，SETE变形后硬度沿中心线呈对称分布，且越靠近外缘，硬度越高，其平均硬度值比CEC的高6.1HV。

[1] LOWE T C, VALIEV R Z. Overview and Outlook for Materials Processed by Severe Plastic Deformation[J]. Springer Netherlands, 2000, 26(4): 187-195.

[2] 史庆南, 王效琪, 起华荣, 等. 大塑性变形的研究现状[J]. 昆明理工大学学报, 2012(2): 23-38.

SHI Qing-nan, WANG Xiao-qi, QI Hua-rong, et al. Research Status of Severe Plastic Deformation[J]. Journal of Kunming University of Science and Technology, 2012(2): 23-38.

[3] FURUKAWA M, HORITA Z, LANGDON T G. Factors Influencing Microstructures Development in Equal-channel Angular Pressing[J]. Metals and Materials International, 2003, 9: 141-149.

[4] SEGAL V M. Materials Processing by Simple Shear[J]. Materials Science & Engineering A, 1995, 197(2): 157-164.

[5] VALIEV R Z, KOZLOV E V, IVANOV Y F, et al. Deformation Behaviour of Ultra-Fine-Grained Copper[J]. Acta Metallurgica et Materialia, 1994, 42(7): 2467-2475.

[6] RICHERT M, LIU Q, HANSEN N. Microstructural Evolution over a Large Strain Range in Aluminium Deformed by Cyclic-Extrusion-Compression[J]. Materials Science & Engineering A, 1999, 260(1/2): 275-283.

[7] LEE S W, YEH J W. Microstructural Evolution and Superplasticity of Al-5.8Mg-0.23Mn Alloys Processed by Reciprocating Extrusion[J]. Metallurgical & Materials Transactions A, 2005, 36(8): 2225-2234.

[8] LIN J, WANG Q, PENG L, et al. Microstructure and High Tensile Ductility of ZK60 Magnesium Alloy Processed by Cyclic Extrusion and Compression[J]. Journal of Alloys & Compounds, 2009, 476(1/2): 441-445.

[9] SHE J, PENG P, TANG A T, et al. Novel On-Line Twist Extrusion Process for Bulk Magnesium Alloys[J]. Materials & Design, 2019(182): 108-111.

[10] TOMASZ, BULZAK, ZBIGNIEW, et al. Technological and Construction Aspects of the Process of Hot Extrusion of Twist Drills Science Direct[J]. Journal of Manufacturing Processes, 2019(45): 123-137.

[11] BEYGELZIMER Y, VARYUKHIN V, SYNKOV S, et al. Useful Properties of Twist Extrusion[J]. Materials Science and Engineering A, 2009, 503(1): 14-17.

[12] 王成, 李萍, 薛克敏, 等. 纯铜挤扭工艺数值模拟与实验研究[J]. 中国有色金属学报, 2011, 21(12): 3071-3075.

WANG Cheng, LI Ping, XUE Ke-min, et al. Numerical Simulation and Experimental Research on Pure Copper by Twist Extrusion[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(12): 3071-3075.

[13] 李萍, 朱慧玲, 严思梁, 等. 低活化马氏体钢热变形行为及机理型本构建模研究[J]. 原子能科学技术, 2020, 54(10): 1904-1911.

LI Ping, ZHU Hui-ling, YAN Si-liang, et al. Hot Deformation Behavior and Physically Based Constitutive Modeling of Low Activation Martensitic Steel[J]. Atomic Energy Science and Technology, 2020, 54(10): 1904-1911.

[14] RAFIZADEH E, MANI A, KAZEMINEZHAD M. The Effects of Intermediate and Post-Annealing Phenomena on the Mechanical Properties and Microstructure of Constrained Groove Pressed Copper Sheet[J]. Materials Science & Engineering: A, 2009, 515(1/2): 162-168.

[15] 薛克敏, 盛杰, 严思梁, 等. 模压变形低活化马氏体钢沉淀相对其力学性能的影响[J]. 金属学报, 2021, 57(7): 903-912.

XUE Ke-min, SHENG Jie, YAN Si-liang, et al. Influence of Precipitation of China Low Activation Martensitic Steel on Its Mechanical Properties after Groove Pressing[J]. Acta Metallurgica Sinica, 2021, 57(7): 903-912.

Comparative Study on Strain Characteristics and Microstructure Analysis of Different Large Plastic Deformation Based on Finite Element Method

HU Qing-hang, TIAN Wen-chun, LI Ping

(School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

The work aims to investigate the deformation characteristics of CEC and SETE, and study the metal flow behavior and strain distribution after single pass deformation. With low activation steel as material, the finite element simulation analysis of the deformation processes under CEC and SETE was carried out, and the equivalent strain cloud diagram of CLAM steel after three passes of deformation was obtained. At the same time, relevant tests were carried out to verify the accuracy of finite element simulation. Both CEC and SETE could realize multi-pass cumulative strain, in which the single pass cumulative strain of SETE was greater, and the equivalent strain of each pass was 2.47, 5.06 and 7.84 higher than that under CEC respectively. After 0.5 pass deformation, the average hardness value under SETE was 6.1HV higher than that under CEC. After each pass deformation under CEC and SETE, the edge equivalent strain is higher than that of the center, and the strain uniformity after 1 pass deformation has little difference, but the strain distribution under SETE is more uniform with the increase of passes. After 0.5 pass deformation, the grain size at the edge under CEC and SETE is smaller than that at the center, and the refinement degree under SETE is higher.

strain distribution characteristics; finite element simulation; deformation behavior; large plastic deformation

10.3969/j.issn.1674-6457.2022.09.002

TG376.2

A

1674-6457(2022)09-0010-08

2022–01–19

国家自然科学基金（51875158，51975175）

胡晴航（1997—），男，硕士生，主要研究方向为精密塑性成形新工艺。

李萍（1973—），女，博士，教授，主要研究方向为晶体塑性、人工智能和精密塑性成形工艺。

责任编辑：蒋红晨