一种基于信息熵的城市轨道交通列车运行控制系统运维分析方法
李靖兰,谭力天,王志伟
(湖南中车时代通信信号有限公司,湖南 长沙 410005)
0 引言
列车运行控制(简称“列控”)系统中,基于通信的列控系统(communication based train control,CBTC)以及全自动驾驶系统的列控系统在城市轨道交通(简称“城轨”)运输中获得越来越广泛的应用。在其正常运行过程中,各子系统间进行数据实时交互,每个子系统都会产生大量的运维数据用以支撑运维工作。随着智慧城轨的发展,列控系统的应用规模及其复杂度不断增加,其运行环境从封闭环境延伸到复杂网络化环境,导致系统运维过程产生大量混杂数据,不易被直观分析[1]。
针对列控系统投入运营后的运维工作研究主要是集中在:(1)轨道交通列控系统可靠性计算与运维策略优化研究,以可靠性建模、综合保障运维策略为依据,为系统主动运维提供理论支撑[2‐3];(2)部署大量传感监测设备用于实时监控、健康状态预测和故障诊断等[4]。对于列控系统运维工作的开展、评判和优化,更多是凭借相关的经验、知识和数据进行相应的处理并根据处理结果做出评判,与系统客观真实情况存在一定偏差。目前,缺乏独立于系统设计,只根据真实运维数据就能直观反映系统运维过程的大数据特性及有序性并能对系统进行客观、综合和量化评判的指标,以及缺乏对系统进行优化、改进的依据和方法。
本文基于大量列控运维数据和信息熵对列控系统进行研究,对系统中个体事件进行量化,以便找出系统事件间的相关性和差异性,消除系统运维过程中的无序性;通过研究不同信息对系统的影响,以便支撑系统的改进优化。
1 列控系统的构成及典型故障事件
1.1 列控系统构成
列控系统通常由列车自动防护(automatic train protection,ATP)系统、列车自动运行(automatic train operation,ATO)系统、区域控制(zone controller,ZC)系统、联锁(computer interlocking,CI)系统、列车自动监控(automatic train supervision,ATS)系统、数据通信(data communications system,DCS)系统和轨旁设备等[5‐7]构成,其互联关系如图1所示。
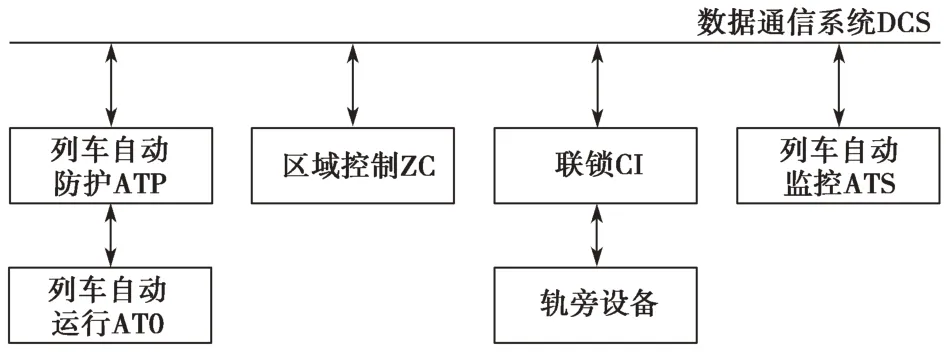
图1 列控系统互联关系Fig.1 Association of the train control system
1.2 列控系统典型故障事件
列控系统子系统间的耦合性较强,需要相互协作才能保障列控系统以高效率正常运行。其中,车载ATP系统与ZC系统为强相关子系统。
涉及车载ATP的故障主要有:(1)ATP‐ZC通信故障;(2)ATP‐ATS 通信故障;(3)ATP‐CI 通信故障;(4)ATP‐ATO 通信故障;(5)列车升级CBTC 级别失败;(6)ATP控制列车运行计算异常;(7)除上述6条外的ATP软件运行异常;(8)ATP硬件故障。
涉及ZC 的故障主要有:(1)ZC‐ATP 通信故障;(2)ZC‐ATS 通信故障;(3)ZC‐CI 通信故障;(4)ZC‐相邻ZC通信故障;(5)ZC控制列车升级CBTC级别失败;(6)ZC 控制列车MA 计算异常;(7)除上述6 条外的ZC软件运行异常;(8)ZC硬件故障。
2 列控系统运维信息熵
在列控系统运维中,工作人员通过分析各个子系统记录的数据来解决系统运行中的问题。从信息理论的角度来看,单条运维数据可以表征系统某一时刻的特征信息,而大量运维数据组成的信息集合可以表征系统的大数据特性及有序性。通过对列控系统子系统的事件进行描述及对熵值的大小问题进行分析和评价,明确运维当中需要关注的地方并给出应对措施,对系统运行具有指导意义。本文以车载ATP、ZC 运维数据建立信息熵模型,以列控系统仿真系统为依据,验证信息熵运维分析方法。
2.1 信息熵及其度量方法
熵[1,8‐9]这个概念用于表示一个系统所具有的有序性的程度或奇异性。这种有序性越低,其熵值就越高;反之亦然。熵值越高,说明系统分布越均匀,奇异性越低;熵值越低,说明分布越不规则,奇异性越高[10‐13]。信息熵主要采用量化的形式表达系统的有序程度,从而度量系统信息的大数据特性及有序性。
2.1.1 信息熵模型
假定任意一个列控系统问题事件并以X表示,认为该问题事件可能的取值为x1,x2,…,xn共n个事件,假设问题事件的概率为P(x),则对应的信息熵H(X),可以表示为

信息熵H(X)与事件X的可能离散事件取值x相关。
根据条件概率问题统计学模型特点[14‐15],考虑实时性与存储空间成本,本文采用二元条件概率论模型分析列控系统运维问题。已知列控系统问题事件Y已发生,并且事件Y的所有离散事件y1,y2,…,yn都与事件X的所有离散事件x1,x2,…,xn条件相关,称其为联合概率分布。在事件Y取不同值的前提下,事件X的信息熵被称为条件熵,可以表示为

式中:H(X|Y)表示条件熵;P(x,y)表示事件x与y一同发生的联合概率分布;P(x|y)表示事件x在事件y已发生前提下的条件概率。
2.1.2 信息熵的度量方法
为方便计算和度量熵值,首先需要获得已知的联合概率分布,在实际应用中需要近似估计概率分布。常见的概率分布或熵度量方法包括:直方图度量法和高斯核函数度量法等。直方图度量法简单、直观,可以快速、清晰地了解信息熵值;但应用于二维以上空间时,其所近似的概率分布与真实的分布情况存在一定的差异[10]。本文采用二元条件概率,从而应用直方图度量法。
直方图度量是根据大数定理,以获得的经验样本数据为依据,获得样本中的概率近似分布。列控系统问题事件x的概率P(x)可以表示为

式中:e(x)为问题事件x计数函数;k为采样样本的数量。
在样本中以相同方式获得二元联合概率分布,则问题事件x与y的联合概率分布P(x,y)可以表示为

式中:e(x,y)为问题事件x与y一同发生的计数函数。
根据式(3)和式(4)及条件概率定义,问题事件x在问题事件y已发生前提下的条件概率P(x|y)可以表示为

2.2 列控系统运维信息熵计算方法
以车载ATP 运维数据为依据,对应车载ATP 主要故障事件为:(1)x11为ATP‐ZC通信故障,y11为列车转为安全态;(2)x12为ATP‐ATS 通信故障,y12为列车通信故障报警;(3)x13为ATP‐CI 通信故障,y13为列车站台联动等操作无响应;(4)x14为ATP‐ATO 通信故障,y14为列车无法进入自动驾驶模式;(5)x15为列车升级CBTC级别失败,y15为列车运行限速及效率低;(6)x16为ATP 控制列车运行计算异常,y16为列车转为安全态;(7)x17为ATP 软件运行异常,y17为列车转为安全态;(8)x18为ATP硬件故障,y18为列车转为安全态。
以ZC 运维数据为依据,对应ZC 主要故障事件为:(1)x21为ZC‐ATP 通信故障,y21为ZC 向列车发送特殊控制信息;(2)x22为ZC‐ATS 通信故障,y22为ZC通信故障报警;(3)x23为ZC‐CI 通信故障,y23为ZC 通信故障报警;(4)x24为ZC‐相邻ZC通信故障,y24为ZC通信故障报警;(5)x25为ZC控制列车升级CBTC级别失败,y25为与ZC通信列车始终无法升级模式和级别;(6)x26为ZC 控制列车MA 计算异常,y26为ZC 控制列车MA终点异常;(7)x27为ZC软件运行异常,y27为ZC转为安全态;(8)x28为ZC 硬件故障,y28为ZC 转为安全态。
为方便展示运维信息熵计算方法,验证方法的可行性,本文以列控仿真系统为例进行说明,系统运维数据来源为对应仿真系统。采用式(3)~式(5)对车载ATP 主要故障事件、ZC 主要故障事件进行概率统计,并对故障概率分布进行相应的统计学处理,获得的车载ATP主要故障事件概率分布如图2所示,ZC主要故障事件概率分布如图3所示。

图2 车载ATP 主要故障事件概率分布拟合曲线Fig.2 Fitting curve of ATP probability distribution of major failure events

图3 ZC 主要故障事件概率分布拟合曲线Fig.3 Probability distribution fitting curve of ZC major failure events
本文统计数据样本为该列控仿真系统运行产生的运维数据。
根据式(1)与式(2),结合统计获得的概率P(x)与概率P(x|y),计算相应的熵值,其中:
(1)车载ATP主要故障事件信息熵为

(2)车载ATP主要故障事件条件熵为

(3)ZC主要故障事件信息熵为

(4)ZC主要故障事件条件熵为

3 运维信息熵实例分析
以列控系统的仿真系统为例,并以直方图度量方法为准进行运维分析,对本文方法进行应用验证。通过对车载ATP 主要故障事件、ZC 主要故障事件进行测试,直方图度量方法结果如图4所示。图4描述的信息熵为不考虑条件概率的信息熵,条件熵为考虑条件概率的信息熵。

图4 车载ATP 与ZC 故障事件信息熵直方图度量Fig.4 Histogram metric diagram of ATP and ZC fault event information entropy
通过直方图信息熵计算结果可以看到,本方法将系统运行数据转化为量化指标,可以直观反映系统特性,其中车载ATP 主要故障事件信息熵为2.773,车载ATP 主要故障事件条件熵为2.145,ZC 主要故障事件信息熵为2.495,ZC 主要故障事件条件熵为1.922。车载ATP 的信息熵和条件熵均大于ZC 的。根据熵值概念,熵值越高,则有序性越低;系统分布越均匀,奇异性越低。计算结果表明本文所采样数据中,车载ATP运维数据的有序性低于ZC 的,奇异性低于ZC 的。同一系统的条件熵小于其信息熵,表明对系统事件相关性的加深了解可以降低系统信息熵。同时车载ATP条件熵较其信息熵降低22.65%,ZC 条件熵较其信息熵降低22.97%,ZC 条件熵对其信息熵的改善程度优于车载ATP 的,但差距不大,两个系统事件相关性差距不明显。
因此,对两个系统的优化可以优先集中在车载ATP 系统,特别是列车升级CBTC 级别、ATP‐ZC 通信和ATP‐ATS 通信3 个方面;而对ZC 系统的优化,可以在ZC 控制列车升级CBTC 级别、ZC‐ATP 通信和ZC‐ATS通信3个方面。
通过对仿真系统的问题跟踪发现,车载ATP较ZC问题更多,且其中最突出的问题是列车升级CBTC 级别失败,与信息熵计算结果一致。
4 结语
本文提出了一种基于信息熵的城轨列控系统运维分析方法,通过信息熵直方图度量方法与统计学方法建立模型,对列控仿真系统运维数据中车载ATP和ZC的主要故障事件信息熵及条件熵进行了量化计算、比对及分析。结果表明,该方法及模型可以有效应用于列控系统运维量化分析中,且可以根据运维数据获得客观、综合和量化的熵信息,直观反映列控系统运维过程中的特性,并根据熵的结果对系统优化提供依据和方向参考。
在智慧轨道交通建设中,城市轨道交通的智能化运维是一种趋势,而本方法量化评价列控系统运维的大数据特性、有序性、直观性、客观性及广泛的适用性,在实现列控系统运维大数据分析、大系统集成以及综合统筹方面,是有效的手段。但是当考虑二维以上空间时,由于考虑的场景更加细化,涉及的事件变量更多,直方图度量方法所近似的概率分布与真实的分布情况会存在一定的差异。
为此,下一步将对系统高维空间信息熵进行分析研究,在本文方法基础上应用高斯核函数度量方法或其他方法对实际线路列控系统的运维数据进行分析。

