基于改进帝国竞争算法的光伏阵列多峰值最大功率点跟踪研究
臧晓笛,刘 璐
(中车株洲电力机车研究所有限公司,湖南 株洲 412001)
0 引言
光伏阵列表面被云、雾和建筑物等局部遮蔽时,其输出特性功率‐电压(P‐V)曲线存在多个峰值。此时若采用传统的电导增量法[1‐2]和扰动观察法[3‐4],则容易陷入局部极值状态,无法准确地跟踪最大功率点,造成功率损失和能源的浪费。为此,国内外学者提出了利用智能群体算法的最大功率点跟踪(maximum power point tracking,MPPT)策略,并取得了一些成效。比如,文献[5]采用数权重因子和随机差分变异策略优化传统鲸鱼算法的SVR(支持向量机回归)参数,论证了鲸鱼算法在MPPT中的适用性。文献[6]通过引入自适应学习因子改进了鸽群算法,结合算法重启策略构建了MPPT 仿真模型,并讨论了改进鸽群算法在光伏组件MPPT 的应用。文献[7]着眼于收敛速度,提出了一种动态缩减搜索范围的细菌觅食算法,并利用仿真模型探索了细菌觅食算法在多峰值下MPPT 中的应用可行性。文献[8]基于迭代次数的变化,给出了利用非线性变异率改进的粒子群算法,尝试进行多峰值下光伏阵列的MPPT。文献[9]通过引入疫苗库和新型运动方程,搭建了基于免疫萤火虫算法的MPPT 模型,证明了免疫萤火虫算法在MPPT 中的有效性。此外,针对光伏组件P‐V特性存在多峰值的情形,文献[10‐15]的研究成果,论证了天牛须算法[10]、布谷鸟搜索算法[11]、树种算法[12]、蛙跳算法[13]、灰狼算法[14]和蚱蜢算法[15]在局部遮蔽下光伏阵列MPPT中的有效性。但上述研究受算法特性的限制,难以解决跟踪过程的局部最优问题。
根据没有免费午餐定理(no‐free‐lunch theorem,NFL)的理论,各种智能算法在不同的应用领域所表现出的性能完全不同[16],也就是说,抛开应用背景来评述算法的优劣和适用性是没有意义的。帝国竞争算法(imperialist competitive algorithm,ICA)是近年提出的一种新型社会启发式算法,其具有参数配置简单和收敛性好的优点,在解决调度和机械设计等优化问题时表现出较好的性能。但目前已有的研究成果中缺乏ICA 在光伏组件MPPT 的应用中的应用探索。综合考虑NFL 理论和ICA 的优异性能,有必要对其在局部阴影遮蔽下光伏阵列的MPPT 进行深入研究。为此,本文尝试将ICA 引入光伏阵列的MPPT 中。首先,分析标准ICA 在阴影遮蔽下光伏阵列MPPT 中的适用性;接着,针对标准ICA 的不足,从收敛速度和计算精度的角度出发,研究标准ICA 的改进策略,以提高全局寻优能力,加快收敛速度;最后,构建仿真模型,对算法改进前后的跟踪指标进行对比,以进一步论证改进ICA 在局部阴影遮蔽下光伏阵列MPPT 中的快速性和准确性。
1 局部阴影下遮蔽光伏阵列多峰值情况
实际工作时,多采用将若干光伏组件串、并联的方式构成光伏阵列,以提高系统的输出功率。由于光伏组件的输出电流受其表面接收光照强度的影响极大,当局部阴影存在时,组成阵列的光伏组件输出电流各不相同。若光伏串联支路的输出电流大于组成该串联支路的某一组件最大输出电流,则该组件转换为消耗功率的负载,形成“热斑效应”,这会缩短设备使用寿命,甚至损坏组件[17]。
在光伏组件两端并联旁路二极管是一种防止热斑效应的有效手段;但旁路二极管会改变串联支路光伏组件的输出特性,导致该串联支路的输出特性呈现多峰值现象。
为进一步阐述光伏阵列遮蔽现象与输出特性的关系,选取3×1 光伏阵列模拟3 种不同遮蔽情况,具体如图1 所示。图中以颜色区分组件的光照强度,白色表示1 000 W/m2,浅蓝色表示800 W/m2,深蓝色表示600 W/m2。

图1 光伏阵列遮蔽情况示意Fig. 1 Shading diagrams of photovoltaic array
标准工况下,该组件的参数如下:短路电流为1.11 A,开路电压为85 V,最大功率点电压为6.06 V,最大功率点电流为0.89 A,工作温度均为25 ℃。不同场景下光伏阵列的I‐V特性如图2所示。由图可知,场景b和场景c 均存在多峰值现象,且峰值的数量与光照强度的分布相关。多峰值现象的存在极大地增加了跟踪最大功率点的复杂度和难度,而传统的电导增量法和扰动观察法却无法应对。为此,本文拟探索基于ICA的局部阴影遮蔽下光伏阵列MPPT。

图2 光伏阵列输出功率曲线Fig.2 PV array output power curves
2 标准ICA建模及其在MPPT中的适用性分析
ICA 通过模拟帝国殖民地竞争机制建立数学模型[18],主要过程如下:
(1)初始国家形成
在问题的解空间内随机生成m个国家,每个国家由n个优化变量组成,则第i个国家的成本为

式中:z(·)——优化问题中的目标函数,即当前的输出功率值;Pi,n——解空间内的优化变量。
(2)初始帝国的建立
根据成本划分殖民国家和殖民地,采用规范化成本计算第n个帝国的规范化势力,即

式中:c(n)——第n个殖民国家规范化成本。
(3)帝国内部同化
殖民地向其殖民国家的方向移动,实现二者之间的相互影响和学习过程,满足
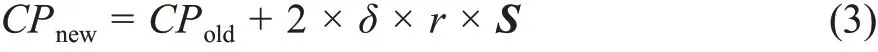
式中:CPold和CPnew——同化前和同化后的殖民地位置;δ——同化系数,本文设δ=2;r——[0,1]内的随机取值;S——殖民地向殖民国家的移动向量。
(4)帝国内部革命
利用内部革命机制保证种群多样性并防止算法局部收敛,则第n个帝国内革命的国家数量为

式中:λ——革命率,一般取λ=0.3[19];Co(n)——第n个帝国内的国家总数。
(5)帝国间合并与竞争
将总成本最大的个体作为势力最弱的帝国,并被势力强大的帝国瓜分。采用轮盘赌的方式给出势力最弱帝国的选择概率:

式中:Ft(n)——利用成本计算所得的每个帝国规范化的势力。
概率最大的帝国获得殖民地。如果最弱的帝国殖民地被全部瓜分,则帝国崩溃。将此帝国删除,并更新帝国的位置和成本,直至算法收敛。
利用标准ICA模型,将电压作为优化变量,组成各个国家集合。将优化目标设为光伏组件输出功率,即成本函数。通过迭代优化至唯一殖民国家,其成本函数即为最大功率值。通过上述分析可以看出,标准ICA算法在局部遮蔽下光伏阵列的MPPT 中是适用的。但采用标准ICA的MPPT也存在着迭代次数较多和计算时间较长的弊端,有必要对其进行改进和优化,以得到更好的MPPT性能。
3 ICA的改进研究
标准ICA 的同化和革命为帝国内部的更新,可能出现帝国内部殖民国家长时间不变的情况,导致帝国内的各变量逐渐趋于相似,影响其寻优性能。下面拟对ICA中的同化和革命过程进行改进,以提升帝国内变量的多样性,进而增强光伏阵列全局极值点的跟踪效果。
3.1 二进制交叉改进同化过程
采用模拟二进制交叉的学习方式对同化过程进行改进,以提高算法的全局寻优能力。具体如下:
(1)选择成本最低的殖民地作为最优殖民地,其余殖民地依次向殖民国家a1或最优殖民地a2学习。为给出殖民地h的学习对象,根据总成本ca1和ca2分析选择的概率:

式中:Pa——优化过程中向最优殖民地学习的概率。
(2)若r<Pa,则殖民地h向殖民国家学习;否则,向最优殖民地学习。如果该殖民地为最优殖民地,则向殖民国家学习。学习的过程为
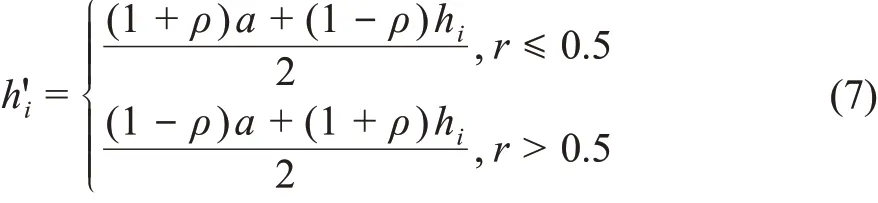
式中:hi——更新前的殖民地位置;h'——更新后的殖民地位置;a——殖民国家或最优殖民地的位置;ρ——位置更新的介质因子,其取值如式(8)所示。
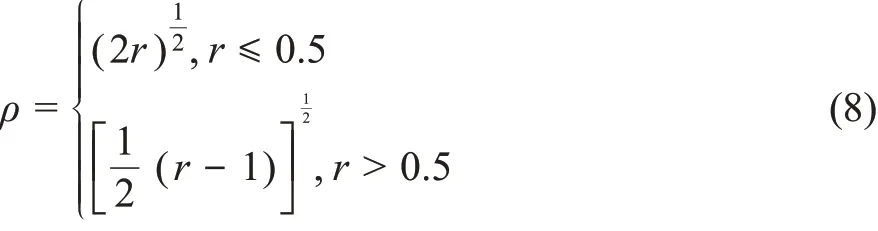
(3)学习完成后,比较各殖民地与最优殖民地和殖民国家的成本关系。若优于原始解,则替换;否则,继续进行革命。
3.2 构造自适应因子优化革命过程
为丰富变量的多样性,采用自适应革命因子对其进行改进,并引入第n个帝国第d次迭代的革命因子:

式中:Fmax——最大的帝国规范化势力;dmax——最大迭代次数。
3.3 择优机制的确定
为提高算法的收敛速度,需在同化和革命过程结束后增加择优机制,以达到在保留初始帝国优秀因子的同时缩短ICA 收敛时间的目的。将各殖民地和殖民国家相结合并对其成本进行排序,选择成本较小者作为新帝国。根据新帝国内部个体的势力值选择最强的个体作为殖民国家,并更新帝国的位置和总成本。
改进后的ICA通过模拟二进制交叉的同化学习方式增加了帝国内部殖民地的多样性,采用自适应的革命方式提升了算法的局部搜索能力,引入最优值选择机制保留了原始帝国优秀基因的同时加快了算法的收敛速度。改进后的ICA整体流程如图3所示。
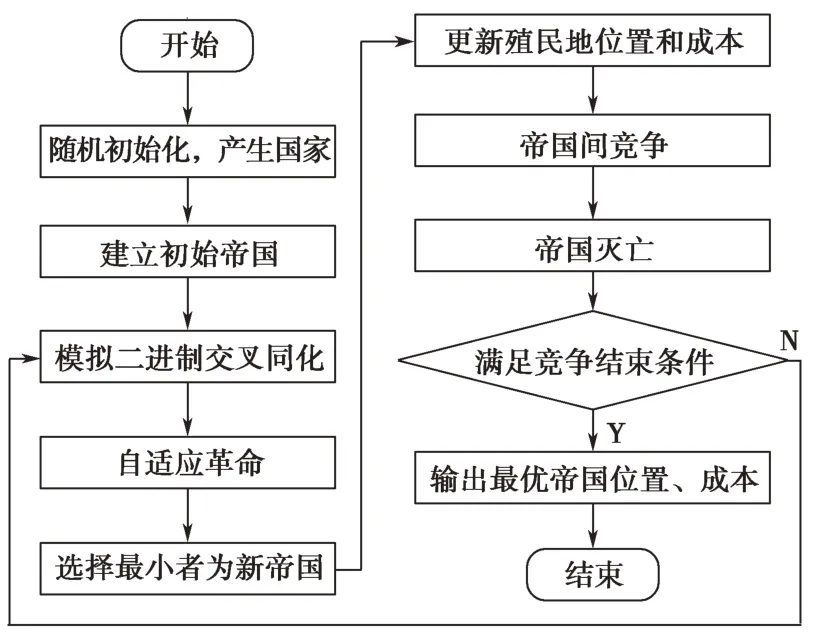
图3 改进ICA 流程图Fig.3 Flowchart of the improved ICA
可见,改进ICA进一步提高了收敛速度、增强了全局搜索能力,提升了优化问题的求解精度,不仅同样适用于局部遮蔽下光伏阵列的MPPT,且有望获得更好的最大功率点跟踪效果。
4 仿真对比分析
为进一步验证标准ICA及所提的改进ICA方法在局部阴影遮蔽下MPPT 中应用的可行性和优越性,构建了如图4所示的仿真模型,并利用S‐fun函数编写算法的MPPT程序;基于图1所示的遮蔽分布,采用标准ICA和改进ICA分别进行静态和动态仿真分析。
4.1 静态对比分析
为验证改进ICA 的性能,首先将整个优化群体设置为30个国家,每个国家由优化变量即光伏阵列电压形成,其中初始帝国为随机初始形成的国家中光伏阵列功率较大的4个;然后,设置最大功率点跟踪过程中的dmax=20。
根据图4所示模型,对图1(a)支路在标准工况下的光伏阵列(各光伏组件接收的光照强度皆为1 000 W/m2)进行MPPT 仿真分析,得到标准ICA 和改进ICA 下的MPPT曲线,如图5所示。由图可知,虽然采用标准ICA和改进ICA 均能得到最大功率位置,但是前者需迭代9 次才能得到最优值,而后者只需迭代3 次即可,大大减少了迭代次数,加快了收敛速度。这证明了所提改进方案的可行性。

图4 光伏MPPT 仿真模型Fig.4 Photovoltaic MPPT simulation model

图5 标准工况下不同算法下的MPPT 进化曲线对比Fig. 5 Comparison of MPPT evolution curves of different algorithms under the standard conditions
为进一步证明该算法在局部阴影遮蔽工况下的最大功率点跟踪效率,对图1(b)支路的局部阴影遮蔽工况(光伏阵列中组件A和组件B的光照强度为1 000 W/m2,组件C 的光照强度为800 W/m2)进行仿真分析。标准ICA和改进ICA的性能仿真过程如图6所示。
图6(a)和图6(c)分别为ICA 的电压和功率跟踪仿真结果,图6(b)和图6(d)为改进ICA的电压和功率跟踪仿真结果。采用改进ICA 在静态局部阴影遮蔽工况下能有效寻得最大功率点,跟踪的时间为0.18 s;相对标准ICA,其收敛速度加快了0.17 s,且输出功率的波动性更小。因此,改进后的算法能够在静态局部阴影遮蔽工况下准确、稳定地跟踪最大功率点。


图6 静态MTTP 结果对比Fig. 6 Comparison of static MTTP results
此外,需要说明的是,在算法寻优得到准确的最大功率点后,采用图4 所示模型进行仿真分析时,由于图4 模型采用的是电导增量法追踪最大功率点,因此在最大功率点附近仍然具有一定的波动性,波动幅值和图4 模型中占空比的步长有关。本文给定的步长较小,并且为直观描述寻优过程的波动情况,作图时选取的纵坐标尺度较大。如图6(a)中局部放大图所示,光伏组件在达到最大功率点后仍存在极小幅度的波动。其他MPPT 过程也存在此现象,但此波动对MPPT 的结果不产生影响,因此未在其他作图中进行标注。
4.2 动态对比分析
为模拟实际运行时光照强度发生变化时的情况,进一步分析此类动态扰动对所提算法的影响效果,设置如下场景:
(1)0 ~ 1 s 时刻,光伏组件接收的光照强度如图1(b)所示,阵列出现局部阴影,组件A和组件B的光照强度为1 000 W/m2,组件C的光照强度为800 W/m2。
(2)1~2 s时刻,局部阴影情况如图1(c)所示,各组件所接收的光照发生变化,组件A光照正常,组件B和组件C的光照强度分别为800 W/m2和600 W/m2。
按照上述光照强度的变化情况,标准ICA 和改进ICA 动态仿真模拟的输出功率变化情况如图7所示。
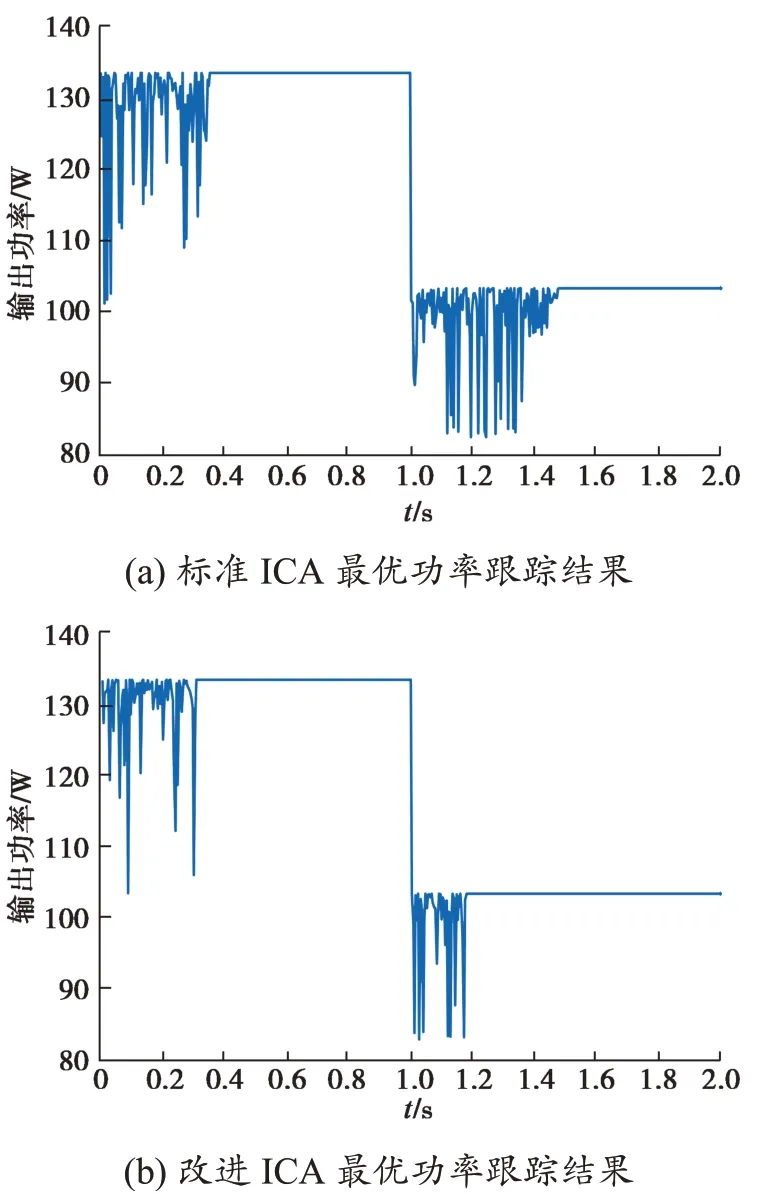
图7 动态局部阴影遮蔽工况下功率跟踪结果对比Fig. 7 Comparison between dynamic local shadow power tracking results by standard ICA and the improved ICA
由图7可知,在光照强度变化的工况下,采用改进算法后的追踪时间为0.19 s,而采用标准算法时所用追踪时间为改进算法的2倍以上;最大功率由133.46 W降为103.27 W,变化完成后的输出功率与最大功率理论计算值[20]的误差为0.9%。综上,改进后的ICA 不仅能够对不同阴影条件下的光伏阵列实现快速、准确的跟踪,而且在光照强度变化的情况下缩短了动态响应时间。
可见,采用标准ICA 能够实现局部阴影遮蔽工况下光伏阵列的MPPT;同样,所提改进ICA算法同样适用于局部阴影遮蔽工况下光伏阵列的MPPT,且具有更好的跟踪精度和更快的响应时间。
5 结语
本文在探索了标准ICA在阴影遮蔽工况下光伏阵列MPPT 中适应性的基础上,提出了一种基于ICA 的最大功率跟踪方法,其在算法的同化和革命环节引入了模拟二进制交叉学习方式和自适应革命因子,并在革命完成后增加了最优值选择机制。改进ICA 增强了算法前期的全局寻优能力和后期的局部搜索性能,提高了迭代速度。同时搭建了MPPT仿真模型,并分别对光照强度不变的静态工况和光照强度突变的动态工况进行了仿真验证。改进ICA 在不同局部阴影遮蔽工况下,MPPT 精度高、速度快,跟踪时间为标准ICA 的50%左右。在光照动态变化的环境下,能显著缩短响应时间,减少能量浪费。后续,可尝试将所提方法与其他元启发算法相结合,以给出更高效、更准确的跟踪策略。

