固体火箭发动机加压固化压强优化设计①

缪求文，申志彬*，崔占鑫，崔辉如

(1.国防科技大学，长沙 410073;2.空天任务智能规划与仿真湖南省重点实验室，长沙 410073;3.陆军工程大学 国防工程学院，南京 210007)

0 引言

相对于装填式固体火箭发动机而言，贴壁浇注式固体火箭发动机具有制作工艺简便、装填量大等优点。但由于发动机壳体与推进剂药柱热膨胀系数相差一个数量级左右，药柱在固化降温载荷下会产生较大的残余应力应变。随着发动机装填分数的进一步提升，加上长期贮存期间推进剂化学老化的影响，固化降温载荷对发动机的药柱结构完整性影响愈加显著。

为降低固化降温载荷对药柱结构完整性的影响，引入了加压固化成型技术。所谓的加压固化法，就是在推进剂固化时通过对药浆加压，使壳体产生初始膨胀，并在固化后降温过程中按照一定路径撤销内压，以实现壳体卸压变形与药柱降温变形的匹配，进而消除部分壳体对药柱表面的变形限制。美国Pratt &Whitney's固体火箭公司在某型号固体火箭发动机制造时，在推进剂固化过程中，采取了对发动机壳体施加内压的工艺用以提高发动机性能。法国学者DAVID在计算推进剂在贮存和飞行载荷下的粘弹性响应时，考虑了加压固化工艺的影响。目前，国内对加压固化技术展开了初步的研究。宗路航等对加压固化的理论压强进行了推导并提出了一种适用于加压固化有限元仿真的两步分析法；刘仔等在考虑药柱脱模等因素的基础上对某发动机进行了理论推导和仿真分析；梁党通等完成了国内首次固体推进剂加压固化试验，明确了加压固化成形技术的有效性；CUI等分析了不同压力值和不同降温降压速率对残余应力应变的影响。现有文献表明，国内研究主要通过体积收缩量计算加压压强，存在较多的经验参数取值，且并未深入分析壳体卸压收缩对加压固化效果的影响。而现有的仿真分析方法未考虑药柱的初始变形，与实际工艺尚有偏差。总的来说，现有的加压固化研究尚不能很好地满足工程应用需求。

本文基于现有加压固化数值分析方法，提出一种能够考虑药柱初始变形的三步分析法；并在已有研究的基础上，从消除壳体对药柱外表面的变形约束出发，分析壳体的轴向变形和径向变形在固化降温过程中对药柱结构完整性的影响；最后对某型发动机的最优加压压强进行优化设计，并总结了基于数值分析的固体发动机最优加压压强设计方法。

1 加压固化原理

加压固化工艺可分为三步：第一步，加压固化浇注阶段，与常压浇注的区别在于药浆浇注完成后，通过加压设备在药浆表面加压，壳体将在压强作用下发生膨胀；第二步，保温保压固化阶段，发动机内保持硫化温度与稳定内压，直至固化反应完成；第三步为卸压降温阶段，在推进剂固化反应完成后，在药柱冷却至室温过程中，按照既定速率进行卸压。加压固化工艺流程如图1所示。

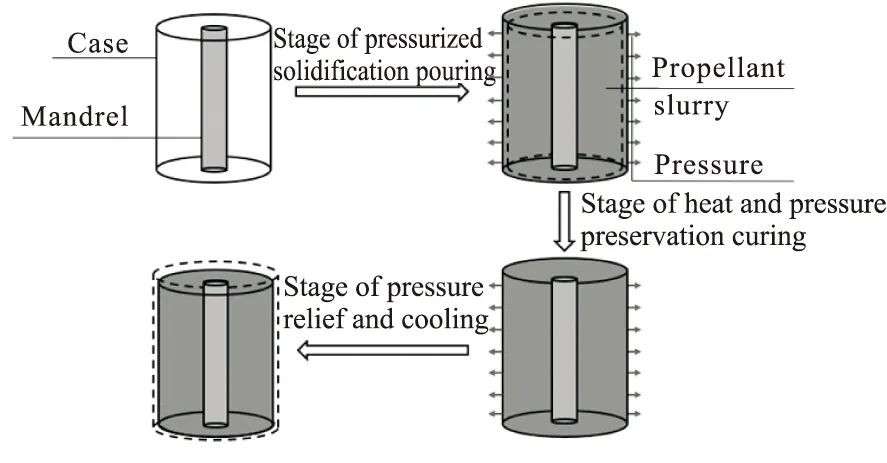
图1 加压固化工艺流程图Fig.1 Flow chart of pressure curing process

2 加压固化仿真分析

2.1 三步分析法

为准确分析加压固化过程的药柱结构完整性，基于原有的两步分析法进行改进，提出一种能够考虑发动机初始变形且适用于自动化分析的仿真分析方法。

基于实际的加压固化工艺流程，确定加压固化载荷下的发动机仿真分析基本步骤如下：第一步，建立加压固化浇注阶段的壳体模型，基于发动机初始几何构型建立壳体有限元模型，并在壳体外表面施加大小为-的压强，记录加压膨胀后的壳体外形参数；第二步，建立保温保压固化阶段的发动机模型，基于第一步的壳体外形参数，利用参数化建模技术，构建考虑药柱体积变化的发动机有限元模型；第三步，建立卸压降温阶段的仿真模型，对第二步构建的模型在壳体外表面施加大小为的压强并施加降温载荷。其仿真流程图见图2。

图2 加压固化仿真流程图Fig.2 Flow chart of pressure curing simulation

2.2 常压固化仿真分析

以某长径比为3.0的翼柱形药柱固体发动机为研究对象，对其进行固化降温载荷下的仿真分析。根据发动机的循环对称性，建立1/18模型，考虑到网格无关性以及计算时间成本，将其划分六面体网格，数量控制在40 000左右，几何模型如图3所示。图3中，点为壳体直线段与头部椭圆段交界点，点为壳体直线段中点。其中，轴向位移约束设置在壳体点所在横截面处。

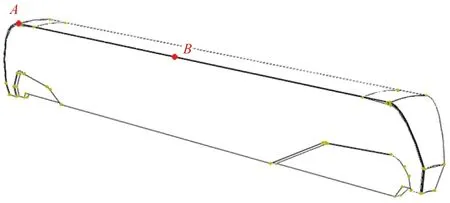
图3 发动机几何模型示意图Fig.3 Geometric model schematic diagram of the SRM

壳体、绝热层和药柱的原始材料参数如表1所示。衬层与药柱材料属性相同，用Prony级数形式表征粘弹性推进剂的松弛模量，如式(1)所示。推进剂前4阶参数如表2所示。

表1 发动机材料参数Table 1 Material parameters of the SRM

表2 推进剂模量Prony级数Table 2 Prony series of propellant modulus

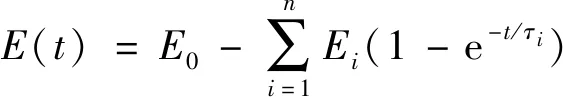
(1)

推进剂材料的时间-温度等效因子的WLF方程见式(2)：

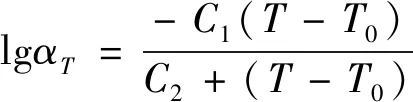
(2)

式中、为材料常数，由材料自身特性决定，=4.971，=156.1；为参考温度，=293.15 K。

本文取零应力温度为58 ℃，对模型施加从58～20 ℃的降温载荷，分析其常压固化后的力学响应。结果显示，药柱中最大主应变为5.205%，最大主应力大小为0.083 6 MPa。

将壳体线膨胀系数修改为与药柱相同后，药柱中最大主应变为0.178%，相比于前，下降了96.58%，药柱中最大主应力为0.008 36 MPa，下降了90.00%。药柱整体趋近于零应力状态，仍存在残余应力的原因在于绝热层的线膨胀系数并不一致。

此时壳体点处径向变形为Δ=-2.689 mm，轴向变形为Δ=-7.137 mm，称此变形为壳体的理想变形条件。

2.3 加压固化仿真分析

为分析加压固化下壳体收缩变形与需求变形之间的关系，先单独对加压固化背景下的壳体变形进行分析。取点进行分析，壳体在不同压强下加压固化时，其径向变形由温度变形、机械变形两部分组成。即

Δ=Δ+Δ

(3)

式中 Δ为点径向总变形；Δ为降温导致的径向变形；Δ为外力导致的径向变形。

为得到点径向变形在不同加压条件下的数学表达式，分别对固体发动机模型单独在降温载荷和卸压载荷以及联合作用下进行仿真分析。结果表明，Δ与温度变化Δ呈线性关系，在既定降温条件下为固定值。而对发动机模型的壳体外表面单独施加随时间线性变化的压强载荷时，发现Δ与加压压强基本呈线性关系，通过计算得到壳体径向变形与加压压强的比例系数，代入式(3)得

Δ=-0394-1236

(4)

同理，对点轴向变形而言有

Δ=-0940-0539

(5)

式中为加压压强，且≥0。

联立式(4)、式(5)得壳体卸压变形关系式：

Δ=1762+2293Δ

(6)

其中，Δ≤-0.940 mm，将卸压变形路径与理想变形点绘制于图4。

图4 B点卸压路径示意图Fig.4 Schematic diagram of pressure relief path at point B

由图4可得，对于该型发动机而言，加压固化工艺无法使壳体达到理想变形条件，只能消除部分壳体对药柱表面的变形限制。当径向变形满足理想变形条件时，轴向变形不满足；当轴向变形满足理想变形条件时，径向变形不满足。

这意味着在加压固化过程仅改变加压压强时，只能消除部分壳体对药柱外表面的变形约束，无法使药柱的结构完整性达到无约束的最佳情况。

3 加压固化压强分析

3.1 加压压强估算

在无法满足理想变形条件的情况下，为确定最优的加压压强，就需要确定壳体在何种变形状态下药柱的残余应力应变最小。首先进行药柱最大主应变关于壳体轴向变形和径向变形的灵敏度分析。

本节中的灵敏度分析借助参数化建模技术，利用正交试验优化设计方法进行，共获得481组不同壳体轴向与径向变形条件药柱中最大主应变数据。其中，不同模型的建立和结果提取使用统一的脚本进行，尽可能降低人工介入导致的误差，灵敏度分析三维曲面图如图5所示。

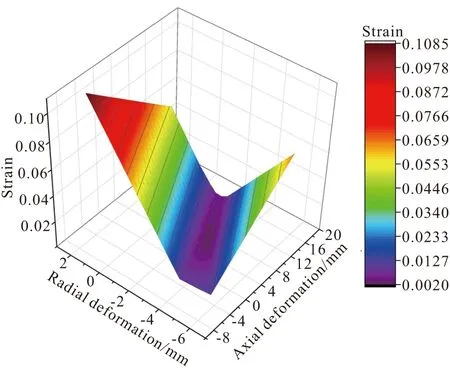
图5 壳体变形-最大主应变三维示意图Fig.5 Three-dimensional schematic diagram of case deformation vs maximum principal strain

从图5可以看出，壳体的轴向和径向变形都能对药柱结构完整性产生较大的影响。相对而言，壳体径向变形的影响更为显著，其原因可能是前后两侧脱粘层的存在已经消除了部分壳体对药柱的轴向变形限制。因此，在确定固化加压的压强时，可通过径向变形进行初选。

将壳体的理想径向变形代入式(4)，初选加压压强为1.857 MPa。此时，壳体在卸压过程中的径向变形为2.720 mm，轴向变形为1.952 mm，药柱中出现的最大主应变为1.217%，与常压固化相比，降低了76.62%，药柱中的最大主应力为0.024 4 MPa，与常压固化相比，降低了70.81%。

3.2 最优压强确定

Evol优化算法作为典型的全局优化算法之一，通过模拟自然进化的方式引导种群进化，具有较高的鲁棒性和广泛的适用性。为确定加压固化的最优压强，利用Evol优化算法，以加压压强为优化设计变量，药柱中最大主应变最小为优化设计目标，对此发动机进行分析。优化分析数据如图6所示。

图6 最大主应变-加压压强关系Fig.6 Maximum principal strain vs pressure curve

由图6可得，随着压强的增加，药柱中出现的最大主应变先减小再增大，在压强为1.922 MPa处取得最小值。此时，壳体径向变形为-2.793 mm，轴向变形为-1.983 mm，药柱中的最大主应变为1.085%，与常压固化相比降低了79.15%，药柱中的最大主应力为0.023 3，与常压固化相比，降低了72.11%。

综上，对某型发动机确定加压压强时，可以根据壳体径向满足理想变形条件进行初选，即

Δ+Δ=

(7)

联立式(4)，得初选压强计算公式：

=(Δ-Δ)

(8)

再基于此压强进行优化分析，快速确定使药柱结构完整性达到最佳的加压压强。

4 结论

(1)壳体的轴向和径向变形是影响加压固化效果的主要因素。由于加压固化过程中壳体无法同时满足两个方向的变形需求，因此加压固化工艺只能消除部分残余应力应变。

(2)对于发动机的药柱结构完整性而言，壳体的轴向和径向变形都会对其造成影响，并且壳体径向变形的影响会更加明显，其原因可能是人工脱粘层已解除了大部分轴向变形的限制。

(3)某型发动机最优加压压强为1.922 MPa，与常温固化相比，加压固化能使药柱中最大主应变下降79.15%。实际工程中，可以先通过径向变形条件估算加压压强，再基于此压强进行优化分析，确定最优加压压强。