横向过载下固体火箭发动机内弹道特性研究①
田忠亮,李军伟*,黄 刚,王向港,王宁飞
(1.北京理工大学 宇航学院,北京 100081;2.四川航天系统工程研究所,成都 610199)
0 引言
随着地空、空空导弹的发展,对导弹的机动性提出更高要求。导弹在空中进行加速、机动飞行时,会产生一定的轴向、横向过载,导致推进剂装药燃速增加,燃面退移偏离设计状态,发动机内弹道性能发生显著改变,绝热层提前暴露在高温燃气中,严重时导致内绝热防护失效。几十年前美国的AIM-9L格斗导弹就已经达到了机动过载35;近年来,美国的AIM-9X、中国的霹雳10等导弹机动过载能力达60,这就要求发动机在大过载作用下仍能稳定工作。因此,掌握横向过载对发动机工作过程的影响规律,对发动机内弹道性能进行有效地预示,对新型高机动战术导弹研制具有重要意义。
过载对发动机工作性能影响的本质是过载改变了推进剂燃速。目前,使用最多、最广泛的过载燃速模型为GREATRIX的多参数燃速增加模型,根据推进剂配方及相关燃气参数,得到较为普适的多参数过载燃速模型。后来,国内学者万章吉、包轶颖等先后采用GREATRIX燃速增大模型对特定配方的推进剂进行了研究计算,得出了不同过载大小、不同方位角下的燃速变化规律。在对燃速研究的基础上,国内外学者对过载下发动机内弹道性能进行了大量的研究。其中,GREATRIX等研究了横向过载下固体火箭发动机工作过程,预测了横向过载下发动机内弹道性能;NORTHAM等利用离心机,在不同加速度下进行了点火和终止燃烧试验,确定了不同情况下燃烧特性;李桢等利用数值计算和试验对横向过载下内端燃、内外燃两种燃烧方式下发动机内弹道进行了分析;曹军、郭颜红等利用level-set算法对小过载下组合装药内弹道进行了研究;刘中兵等根据几次典型的飞行试验数据,结合喷喉烧蚀情况,总结了飞行过载对发动机内弹道的影响。国内外学者对此进行了很多研究,但是它们大都是对横向过载下管型装药内孔、内外燃,旋转过载下星孔装药进行研究,对横向过载下星孔装药燃烧研究的过载量级较小,小的横向过载对内弹道特性影响不大。目前,对三维复杂药型燃面退移计算方法有Pro/E实体造型法、level-set算法、动网格方法。其中,Pro/E实体造型法不适用不等速的燃面退移;level-set算法是目前对燃面退移模拟最常用的方法,它采用初值形式将一个纯几何问题转变为用偏微分方程描述的数学问题,在燃面退移过程中需解微分方程组,对空间进行离散,计算量非常大,计算精度难把握;动网格技术则是在初始药型上生成非结构网格,利用当地燃速进行退移,再利用网格重构获得新的燃面,通用性较好,但是在处理燃面交汇、分离等拓扑变化的稳定性不好把握。
本文从简单管型装药内孔燃烧拓展到复杂星孔药形,采用数值计算方法,从横向过载(0~150)下装药燃面退移出发,建立了典型装药非均匀燃烧的燃面退移模型,分析了横向过载下发动机的内弹道性能,计算速度快,通用性较好,可为发动机设计人员提供参考。
1 计算方法
1.1 几何模型
本文采用的发动机结构如图 1所示,内径为90 mm。推进剂装药采用管型、星孔两种药型,一个端面和外表面包覆,内表面和另一个端面燃烧。横向过载与发动机轴线方向垂直。

图1 横向过载发动机示意图Fig.1 Schematic for SRM lateral overload
1.2 过载下固体推进剂燃速模型
通常来说,过载会使推进剂燃速增加,但是不同配方推进剂燃速对加速度敏感性不同,导致在燃烧过程中有很大差异。本文使用的推进剂为文献[16]的推进剂,配方为AP/HTPB/Al=75∶15∶10。相关参数如表1所示。

表1 推进剂参数Table 1 Propellant parameters
表1中,为推进剂的燃速系数,得出燃速与加速度的多项式关系如下:

+2636×10×+1
(1)
式中为过载下推进剂的燃速;为推进剂的静态燃速;为过载加速度。
通常来说,推进剂燃烧过程中推进剂表面温度、燃气温度等是不断变化的,由于推进剂点火机制复杂,且点火时间为几十毫秒级,相比之下,本文更加关注的是过载对工作阶段压强的影响,探究过载对工作段压强变化的影响规律。因此,在进行燃速模型求解过程中,忽略了点火过程中推进剂表面温度和燃气温度的变化,燃气温度取推进剂绝热燃烧温度,仅考虑了燃烧过程中燃烧室压强和过载量级的变化对燃速的影响,得到上述过载下推进剂燃速模型。
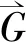
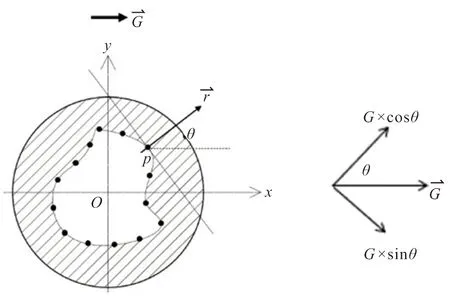
(a)Schematic diagram of lateral overload (b)Exploded diagram of lateral overload图2 横向过载分解示意图Fig.2 Section diagram of lateral overload
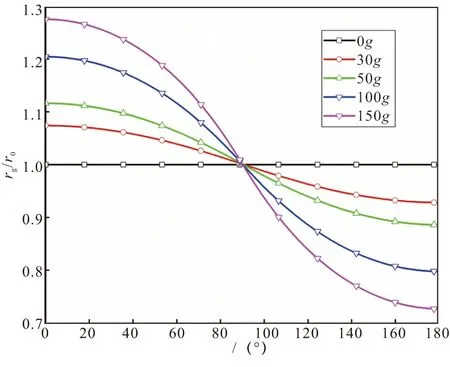
图3 不同过载不同方位角下的燃速情况Fig.3 Burning rate under different overload and azimuth angle
1.3 燃面退移离散坐标求解方法
装药燃面退移离散坐标计算即将整个装药燃面离散成有限多个数据点,把燃面退移问题转化成点的平移问题,对复杂内型面的装药分析起来比较容易。将每个数据点按照该点的燃烧速率平移得到新数据点,并连接成线,得出不同燃烧时间的燃面形状。
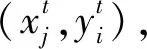
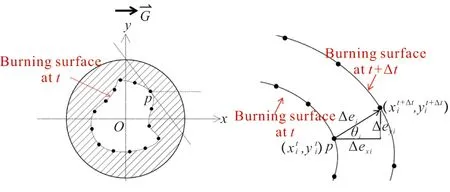
图4 离散点退移示意图Fig.4 Schematic diagram of discrete point regression

(2)
Δ=·Δ
(3)
Δ=Δ·cos
(4)
Δ=Δ·sin
(5)
则在Δ时间内第个数据点的坐标变化为

(6)
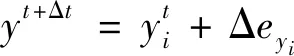
(7)
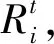
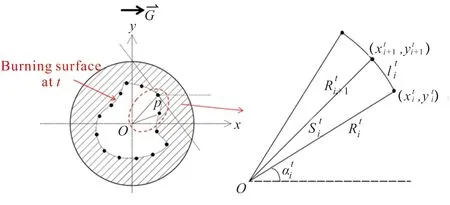
图5 一个计算微元的示意图Fig.5 Schematic diagram of a calculated micro unit
则有

(8)
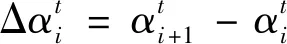
(9)

(10)
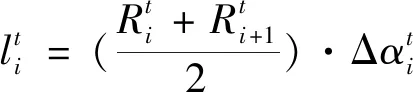
(11)
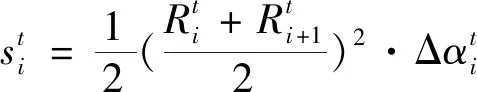
(12)
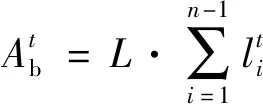
(13)
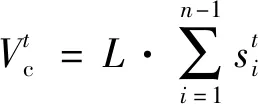
(14)
但是,当存在横向过载时,不同位置燃速差异,使整个装药表面发生偏心,燃烧过程分成几个阶段。其中,内孔燃烧的圆管型装药分成两个阶段。第一个阶段如图6(a)所示的增面燃烧,从开始燃烧到燃速最大处燃烧完毕,、可以直接采用式(8)~式(14)进行求解;第二个阶段为图6(b)所示的减面燃烧,燃速最大处燃烧完毕至装药全部燃烧完。在燃烧完毕区域=0,=/2,未燃烧完的区域仍然按照与第一阶段相同的计算方法。
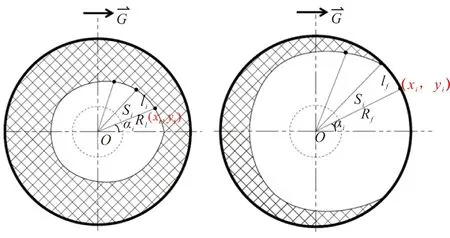
(a)First stage calculation model (b)Second stage calculation model图6 计算模型示意图Fig.6 Schematic diagram of calculation model
1.4 内弹道计算模型
燃烧室压强是固体火箭发动机一个十分重要的参数,是保证发动机工作稳定、正常的必要条件。本文所使用的发动机燃烧室内径为70 mm,结构尺寸很小,燃烧室内燃气流速很小,故把燃烧室内压强看作是均匀的,即“零维”内弹道问题。根据燃气的质量守恒,得出“零维”内弹道下燃烧室压强计算模型:
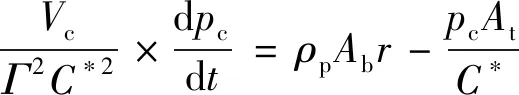
(15)
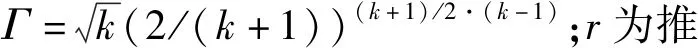
式(15)中,针对的是整个燃面的面积和该所对应的燃速。当不存在过载作用时,和是总体对应的;而在横向过载下,各个位置处的燃速是不同的。因此,在计算过程中,需要将和一一对应。如图5所示,在一个扇形计算微内,对应角度为Δ,认为Δ计算微元内燃速是恒定不变的,则有
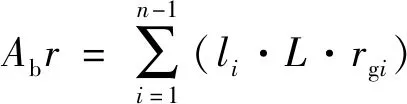
(16)
这样,把每一个微元下的燃速和燃面面积相对应,然后对整个装药进行求和,代入到内弹道求解方程中求解计算。
本文主要探索横向过载对发动机内弹道特性的影响规律,计算过程中使用的发动机内径为90 mm,结构尺寸较小,在计算过程中认为燃烧室内的压强是均匀的,且燃烧过程中每处的燃速是相同的,忽略了侵蚀燃烧的影响。因此,在燃烧过程中将推进剂看作是普通的二维药柱,认为其不具有三维特征。
2 结果与讨论
2.1 方法验证
采用三种不同的验证方式对该计算方法进行验证,分别为level-set水平集方法、国防科大李桢的数值计算方法及轴向过载下的发动机点火试验。
Level-set水平集算法,比较有代表性的为哈工程王革等对二维界面、复杂三维药型的燃面退移模拟。采用文献[20]中的二维方孔、星型的界面参数,将该方法与level-set计算结果及三维UG软件退移结果进行对比,结果如图7所示。由图 7的对比结果可以发现,本文计算方法和level-set方法及三维软件建模方法得到的结果吻合较好,燃烧过程中整体误差在5%以下,与level-set算法计算得到的结论一致,在界面退移即将结束时,误差变大。
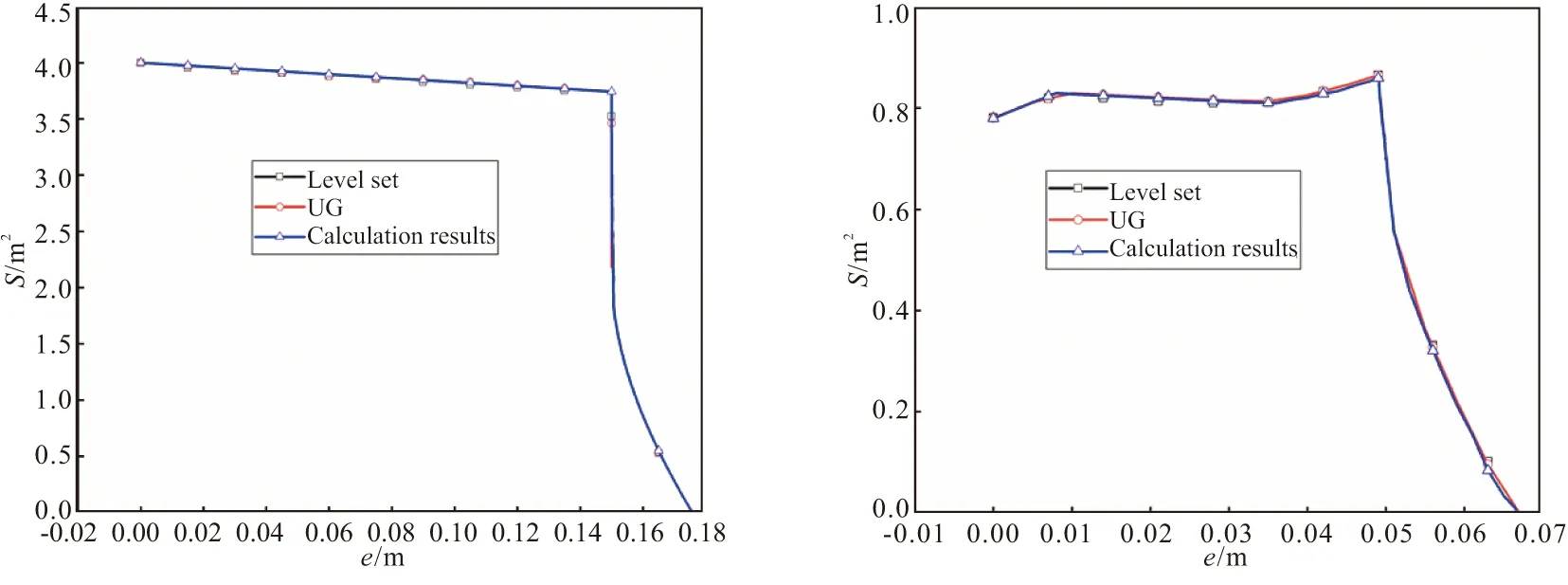
(a)Square hole grain (b)Star grain图7 界面面积变化曲线Fig.7 Change curves of interface area
同时,利用国防科大李桢的几何计算模型对该计算方法进行验证。推进剂采用圆管型装药,外表面和一个端面包覆,内孔+另一个端面燃烧。横向过载下内端燃管型装药,横向过载与端面燃烧方向的夹角为90°,故端面燃速始终为静态燃速,在Δ时间内,装药长度变为-·Δ。“零维”内弹道方程中的可以分成内孔燃面和端面两部分。
端面的燃面面积用式(12)求解:
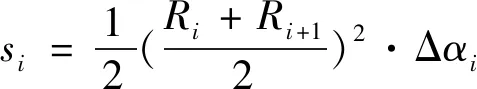
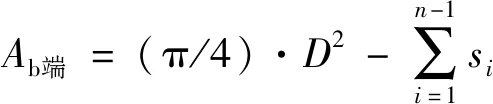
(17)
整个燃面:

(18)
求解得到的燃面面积和内弹道对比分别如图 8、图9所示。可以发现,本文燃面面积的计算结果与文献中结果吻合,验证了该燃面退移求解方法的准确性。在图9中的内弹道曲线对比中,本文计算在整个工作段与文献中的结果相吻合,同时也较好地预测了横向过载下内弹道的拖尾现象,与文献结果整体误差在5%以内,验证了内弹道求解模型的正确性。
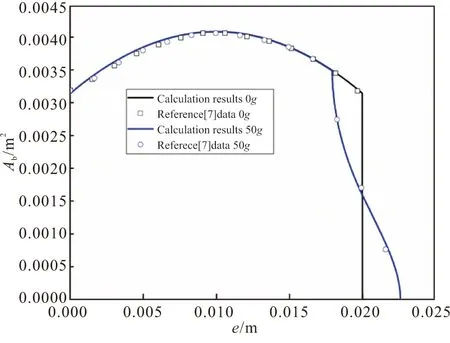
图8 燃面面积对比图Fig.8 Fig.8 Comparison of burning surface area

图9 内弹道对比图Fig.9 Comparison of interior ballistics
同时,开展了管型装药内外燃+一个端面燃烧轴向过载下的点火试验,试验过载工况为10和20,试验与计算结果对比情况如下图10所示。试验验证中0.18 s之前存在偏差,但是大部分工作时间段(0.2~0.8 s)计算结果与试验结果吻合较好,预测了过载下发动机的内弹道特性,尤其是工作段的压强变化。
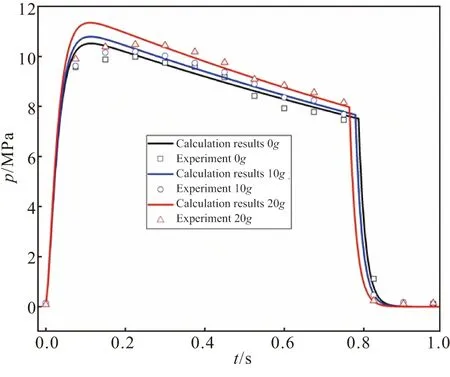
图10 试验计算对比图Fig.10 Comparison of experimental and calculations
采用level-set水平集方法、李桢的计算方法及过载下的发动机点火试验,与本文的计算方法进行对比,验证了计算方法的准确性。下面针对横向过载下管型装药、星孔装药两种不同结构药型内孔燃烧的内弹道特性进行分析。
2.2 算例
2.2.1 管型装药内孔燃烧的内弹道求解
管型装药尺寸如图11所示,装药内径20 mm,外径80 mm,长80 mm,外表面和一个端面包覆。
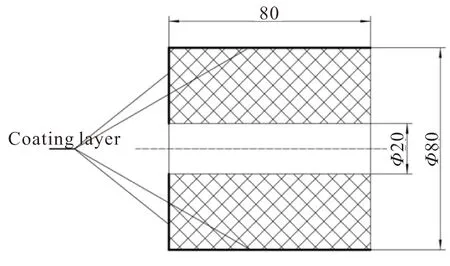
图11 装药尺寸示意图Fig.11 Schematic diagram of grain size
(1)100横向过载下管型装药内弹道求解
根据式(1)的过载燃速模型,对该结构装药进行燃面退移计算,燃面变化情况如图12所示。
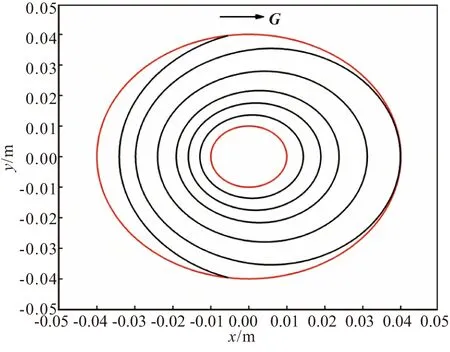
图12 100g过载下管型装药燃面退移示意图Fig.12 Schematic diagram of burning surface regression of tube grain under 100g overload
横向过载导致内孔燃烧管型装药燃面在轴线上发生了偏心,燃速最大位置处燃烧完后,装药变成一个月牙形,燃面面积的变化分成两个阶段。根据图5,<90°的数据点位于第一象限,>90°位于第二象限。如图13所示,在初始时刻,每个微元弧长是相等的,不同,不同位置处的燃速不同,燃速大的位置燃烧肉厚大,对应弧长也大。随着燃烧的进行,第一象限内的燃面逐渐消失。利用式(16)将图13和图14中的数据对应相乘并求和,得到过载下整个燃面的。

图13 100g 过载下装药横截面不同微元的长度Fig.13 Length of different micro elements in grain cross section under 100g overload
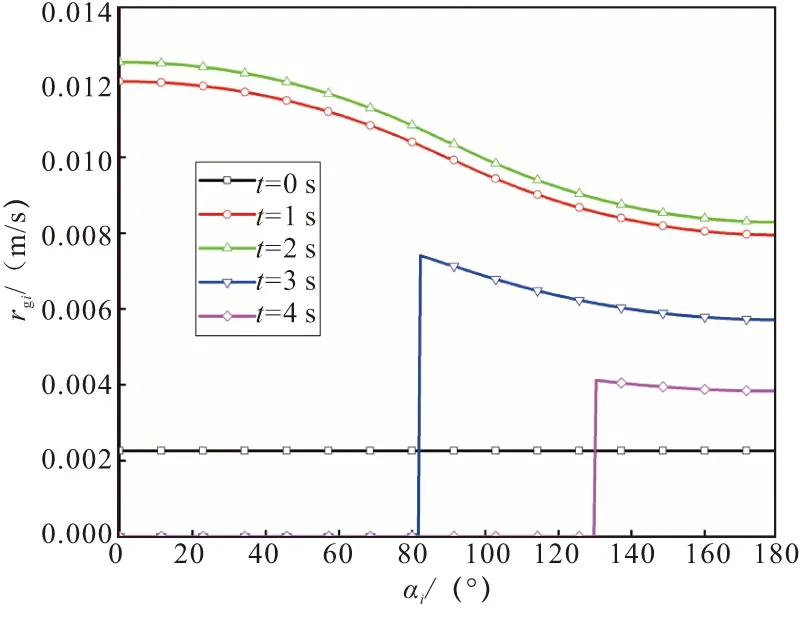
图14 100g 过载下装药横截面不同位置的燃速Fig.14 Burning rate at different positions of the cross section of the grain under 100g overload
(2)不同横向过载下管型装药内弹道求解
按照上述的求解方法,进行0~150不同横向过载下燃面面积和内弹道计算,如图 15、图 16所示。由于燃烧方向与横向过载呈90°位置处的燃速等于静态燃速,即无论过载存在与否,该点的燃面退移情况都是相同的;为便于和无过载的情况进行对比,定义90°方向上的燃烧肉厚为Δ,根据不同角度下的燃速差异,得出其他位置处燃烧肉厚变化情况。
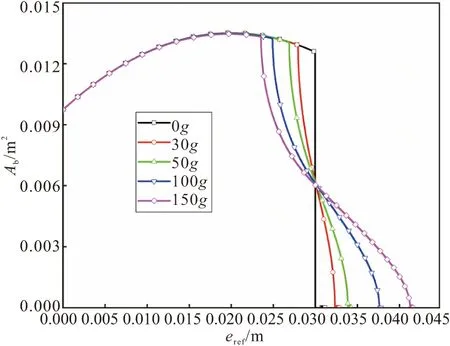
图15 管型装药内孔燃烧的燃面面积变化曲线Fig.15 Burning surface area change curves of tube grain

图16 管形装药的内弹道曲线Fig.16 Interior ballistic of inner of tube grain
从图 15可以发现,受偏心的影响,燃面面积变化分成了两个阶段。在分离点出现之前,过载对燃面面积影响不大,过载导致燃面面积峰值出现时间提前;在分离点之后,燃烧过程变成了一个减面燃烧,整个装药燃烧时间变长。
由图 16可知,相同时刻,燃烧室压强增加,压强峰值出现时间提前;过载导致药柱相对于发动机轴线发生偏移,压强的下降点提前,其中100过载下,下降点提前0.4 s,压强峰值降低了1.2 MPa,燃烧明显拖尾,整个装药的燃烧时间变长;且过载越大,对上述影响越大。
2.2.2 星孔装药内孔燃烧的内弹道求解
星孔装药参数示意图如图 17所示。装药参数如表2所示。

表2 装药参数Table 2 Parameters of the grain
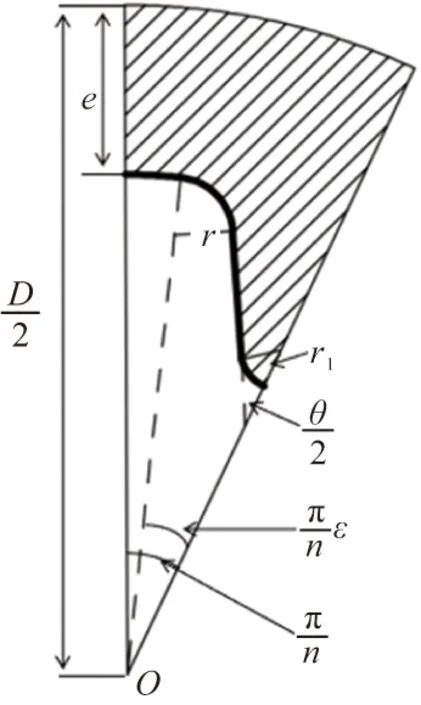
图17 星孔装药参数示意图Fig.17 Schematic diagram of star hole charging parameters
利用式(1)的过载燃速模型,得到的横向过载下的燃面退移规律如图 18所示,横向过载下星孔装药的燃面面积变化曲线如图 19所示。由两个图可以发现,与圆管形装药类似,横向过载导致推进剂燃烧发生明显偏心,燃烧出现分段现象,在分离点出现之前,横向过载对燃面面积影响不大;而下降阶段随着过载的增大时间逐渐变长,管型装药内孔燃烧的下降过程只有一个阶段,而星孔装药在过载大于一定的数值时,会出现明显的分段现象。

(a)0g (b)30g (c)100g图18 不同过载下的燃面退移情况Fig.18 Burning surface recession under different overload
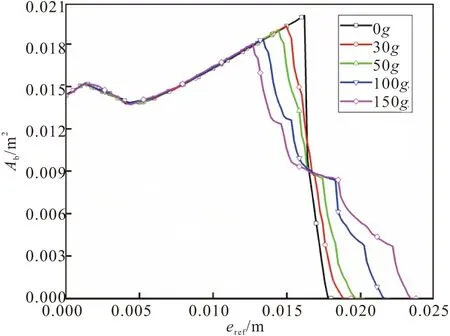
图19 横向过载下星孔装药的燃面面积变化曲线Fig.19 Change curves of burning surface area of star hole lateral overload
为更清晰地表达不同横向过载对燃面退移的影响,对不同过载下,相同燃烧时间燃面情况进行分析。如图20所示,可以发现水平向右的横向过载使得整个燃面在退移的过程中向右偏心,并且过载值越大,偏心程度越大。
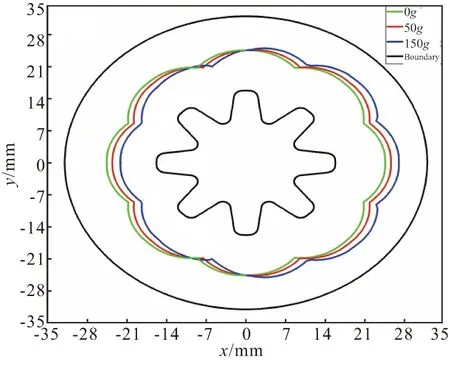
图20 不同过载下1 s时的燃面现状Fig.20 Status of grain burning surface at 1 s under different overload
采用上述计算方法,对横向过载下星孔药型内弹道进行求解,结果如图21所示。从开始燃烧到分离点出现之前,压强变化规律一致,过载使燃烧室压强略微增大,压强峰值减小,出现时间提前,100过载下,压强峰值减小0.8 MPa,时间提前0.3 s;到达分离点后,压强出现下降段,压强下降段也会分成与燃面面积类似的几个部分。压强峰值点就是燃烧分离点,即=0°处燃烧完毕,在这个点处,绝热层将暴露在高温燃气流中,一直到燃烧完毕。所以,过载增加了绝热层的暴露时间。
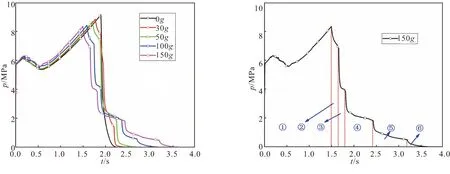
图21 不同过载下的内弹道曲线 图22 150g下星孔装药的内弹道曲线Fig.21 Interior ballistic curves under different overload Fig.22 Interior ballistic curves of star hole grain at 150g
选取如图22分段比较明显的150下内弹道曲线进行研究,分析分段产生原因。150横向过载压强下降段分成5个阶段,由于星角存在,在燃烧的过程中,每个星角处的余药在燃烧过程中也会偏心,每个星角处余药不会同时燃烧完毕。每个星角处余药不同,导致燃面下降阶段就会按照星角数分成不同阶段,结合图 23来分析每个阶段燃烧过程。

(a)t=0~1.49 s (b)t=1.50~1.65 s (c)t=1.66~1.79 s
图 23(a)为 位置(燃速最大的位置、圆弧1上方位角为0°的点)燃烧完毕,压强上升和压强下降分离点,也是绝热层开始暴露的时间点;图 23(b)对应图22中第二阶段,即从绝热层开始暴露到圆弧2上燃速最快的点燃烧完毕,圆弧1的燃烧过程;图 23(c)对应图22中第三阶段,圆弧2燃烧过程;图 23(d)对应图22中第四阶段,圆弧3燃烧过程;图 23(e)对应图22中第五阶段,圆弧4燃烧过程;图 23(f)对应图22中第六阶段,圆弧5燃烧过程。
横向过载对绝热层暴露时间影响最大,定义绝热层暴露时间为绝热层开始暴露到压强下降到压强峰值10%所需要的时间,将几种过载下绝热层暴露时间进行对比,如图 24所示。随着横向过载的增加,绝热层暴露时间近似线性增长,当过载在0~150变化,时间从0.21 s增加至2.29 s,暴露时间增加约10倍,这对发动机的热防护提出了很高的挑战。

图24 不同过载下的绝热层暴露时间Fig.24 Insulation exposure time under different overload
3 结论
(1)横向过载使装药表面上每个点燃速都有差异;通常来说,横向过载使燃烧室压强略有增大,压强峰值减小,出现时间提前,绝热层率先暴露。
(2)横向过载会使推进剂在燃烧过程中产生偏心,燃烧过程出现分段现象;对星孔装药,当燃烧至分离点后,其燃烧过程会由于余药不同继续分成几个阶段,分段数等于星角数/2+1。
(3)燃面下降段几个分段受横向过载大小及推进剂燃速敏感性的影响;星孔装药的下降段的分段数受星角数的影响,燃速增量越大,现象越明显。
(4)本文所使用的离散点计算方法适用于内孔型面为任意形状的装药。

