一种曲面压缩高超声速进气道的设计及流场快速求解方法①

王 鑫，袁化成，刘甫州，张锦昇

(南京航空航天大学 能源与动力学院，南京 210016)

0 引言

进气道是吸气式高超声速推进系统的关键部件之一，直接影响着推进系统和飞行器的综合性能。据分析，对=5～7一级的碳氢燃料飞行器，进气道的压缩效率每提高1%，可使推进系统比冲增加3%～5%，而进气道流量捕获能力则直接影响着发动机推力的大小。因此，高超声速进气道的设计即要满足推进系统在飞行包线内的流量需求，还要保证尽可能小的总压损失。

从20世纪50年代以来，高超声速进气道已发展出多种形式，如二元式进气道、侧压式进气道、轴对称进气道以及三维内转式进气道等。其中，二元混压式进气道兼具外压式进气道和内压式进气道的优点，具有起动能力好、总压恢复系数高、外阻力小等特点，工程应用相对较广，如美国的X-43A、X-43B试验机以及ATR进气道等。早期的二元混压式进气道外压段设计通常为一级或多级压缩，之后张堃元教授提出了以曲代直的设计思路，以弯曲激波代替多级斜激波形成了二元曲面压缩进气道。随后研究表明，曲面压缩进气道在降低总压损失、提升压缩效率、缩短长度、避免附面层分离、改善非设计点性能等方面均存在优势。

针对二元曲面压缩进气道的设计方法大致分为正向设计和逆向设计两类。其中，正向设计通常指定曲面压缩几何规律来研究弯曲激波流场特性，如二次函数形式的压缩曲面，给定沿程曲率或压缩角变换规律的压缩型面，或者是通过压迫等熵压缩型面获得弯曲激波压缩型面的设计方法。总的来看，正向设计方法在本质上是几何设计方法，易于实现，但是设计参数大多没有较为明确的气动意义，不能够直接达到所需的性能需求。而逆向设计方法则是根据性能需求来逆设计压缩型面，此类方法简单精确、适用性广并且针对设计需求的不同发展出了多种实现途径，如基于出口参数分布的逆设计方法、指定压缩面压力分布或者马赫数分布的逆设计方法以及给定激波形状的型面逆设计方法。其中，基于激波形状的型面逆设计方法可以根据需要同时调整几何尺寸、增压比以及激波压缩和等熵压缩的比例，多被应用于进气道和前体的一体化设计中，而基于壁面参数分布的型面逆设计方法能够合理控制压缩面沿程压力分布或沿程马赫数分布，有利于改善压缩面附面层的稳定性，从而有效缩短外压缩段的长度。目前，针对不同逆设计方法的优势已有较多研究。因此，可将不同的设计方法相融合，整合优势，从而获得更为灵活，适用性更广的进气道设计方法。

在高超声速进气道的设计阶段中，通常需要根据进气道流场及性能参数进行大量迭代来实现构型的优化设计。因此，对于进气道流场的高效求解尤为重要。邓隆范和周建兴等曾基于斜激波理论及经验公式对二元混压式进气道进行了性能快速评估和优化设计，但精度相对较低。王宏涛等采用无旋特征线法对进气道压缩段性能进行了快速评估研究，但仅能适用于=4以下进气道，应用范围较窄。目前，对于高超声速进气道流场及性能的求解主要依靠CFD方法，而CFD方法在优化迭代过程中计算耗时相对较长。因此，有必要提出一种进气道流场的快速求解方法，与CFD方法配合使用，完成预研阶段进气道原型方案的快速优化设计。

基于上述分析，本文在高超声速进气道气动设计中，将基于激波形状和基于壁面参数分布的逆设计方法相融合，形成了一套能够同时满足几何限制和气动需求的曲面压缩高超声速进气道设计方法。而后，基于有旋特征线法提出了一种高效的进气道流场求解方法，据此可实现进气道无粘性能的快速求解。

1 进气道型面设计方法

根据弯曲激波压缩进气道的结构特点，本文采用一道弯曲激波+唇罩激波及其反射激波系来减速增压高超声速来流。如图1所示，进气道型面设计也相应的被分为外压段曲压缩面设计、内压缩段设计以及隔离段设计。由于曲面压缩后内压段入口气流速度的方向和大小并不均匀，经过内收缩段后主流区内可能仍然存在较大速度梯度，因此需要在隔离段内继续掺混，从而在进气道出口获得速度大小方向基本一致的高品质气流。

图1 进气道压缩波系配置Fig.1 Schematic of inlet compression model

1.1 外压缩段设计

在高马赫数进气道外压缩段的型面设计过程中，本文将基于弯曲激波形状和基于壁面减速规律这两种型面逆设计方法相融合，如图2所示。当外压缩段长度和进气道捕获高度一定时，通过三次函数关系设计出满足约束条件的弯曲激波形状。然后，根据基于弯曲激波形状的壁面逆设计方法，便可反设计出压缩型面段。之后，根据气动需求指标，调整点至外压段出口截面间的壁面沿程马赫数分布，结合已求解得到的左行特征线，运用基于壁面参数分布的型面逆设计方法，便可反设计出压缩型面段，从而达到调控外压缩段收缩比及唇口截面性能参数的目的。

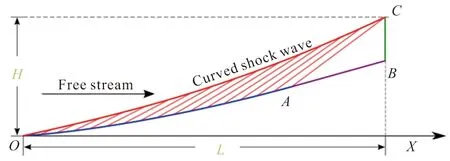
图2 外压缩段型面设计Fig.2 Schematic of inlet external compression section design

基于上述论述，本文采用三次曲线来描述弯曲激波的形状，式(1)为曲线的一般函数表达，对上式求导可得曲线的沿程斜率变化如式(2)所示，其物理含义表示弯曲激波沿波面的激波角变化规律。式中未知参数为、、和。

=+++

(1)

′=3+2+

(2)

在来流条件已知的情况下，由来流马赫数和当地激波角可唯一确定波后的气流方向角。反之，若给定波后气流参数和来流条件，也可求得当地激波角的大小，从而确定三次曲线的沿程斜率变化。因此，通过设置三次曲线起始点的斜率，即可控制压缩型面的起始压缩角。同理，通过调整三次曲线结尾处的斜率，便可获得期望的波后马赫数的大小。如图3所示，在弯曲激波的流向长度为，纵向高度为的情况下，设定弯曲激波的起始点坐标为(0,0)。

图3 弯曲激波构造示意图Fig.3 Schematic of curved shockwave design

当均匀来流马赫数为，压缩型面的起始压缩角为时，由斜激波关系式(3)可解得弯曲激波的起始激波角。同时，由于弯曲激波在本质上是由斜激波与若干压缩波相交偏折形成的，在物理上表现为激波角逐渐增大，对应的数学含义为三次曲线的二阶导数恒大于零(如式(4)所示)。在起始压缩角、长度和高度一定的条件下，可解得的取值范围(如式(5)所示)。再根据斜激波前后马赫数关系式(6)，可确定曲激波端点波后马赫数的取值范围。因此，在外压段几何约束、起始压缩角和激波端点波后马赫数给定的条件下，联立求解式(7)，即可解得、、及的具体数值，从而获得满足几何约束和气动需求的弯曲激波形状。

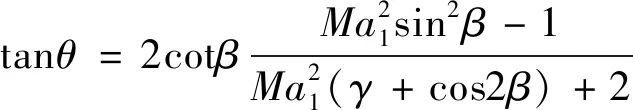
(3)

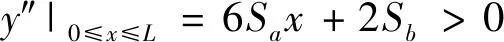
(4)

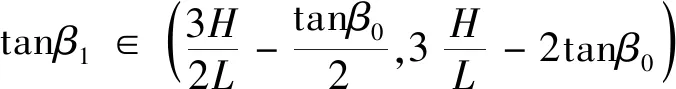
(5)

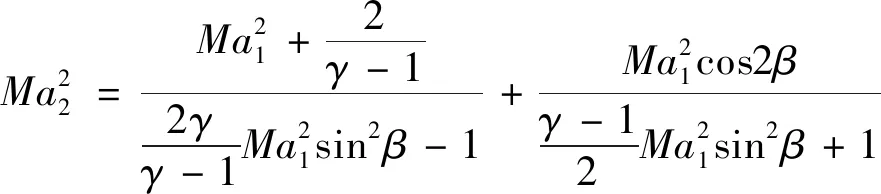
(6)

(7)

在获得弯曲激波形状后，本文采用文献[21]中给出的逆特征线法来反设计压缩型面，其内点单元求解如图4所示。与常规特征线法不同，待解点3点位于2点上游。因此，需根据2点发出的逆特征线确定。求解过程中运用到的特征线方程及相容关系如式(8)～式(12)所示。图5为给定弯曲激波形状求解压缩型面的推进求解过程。

图4 内点单元求解过程Fig.4 Schematic of MOC interior point solution

如图5所示，在已知弯曲激波面上的全部参数后，在每一层内从激波面开始沿流线向下游求解，至结尾特征线时结束，而后开始下一层的迭代求解。整个逆特征线法求解最终得到一个由流线和左行特征线组成的特征线网，其中,,,…,和点连线，即为当前弯曲激波对应的压缩型面。

图5 逆特征线法求解过程(基于弯曲激波)Fig.5 Shematic of inversed characteristic solution (based on curved shock profile)

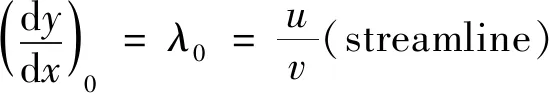
(8)

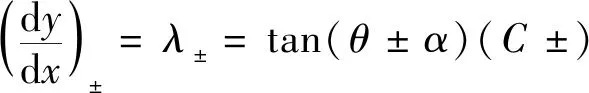
(9)

d+d=0(streamline)

(10)

d-d=0(streamline)

(11)

(12)

在完成图2中段的型线设计之后，通过给定点之后壁面马赫数分布规律后，可根据壁面发出的一簇左行特征线和结尾左行特征线发出的一簇右行特征线两两相交完成壁面(壁面流线)和结尾左行特征线影响域的求解。由于段长度相对较短，故采用如式(13)所示的线性分布规律，其中为点马赫数期望值。

(13)

如图6所示，在整个影响域内多次使用特征线内点单元求解过程，在壁面处采用壁面点求解方法，即可获得区域--内所有点的流场信息。将唇罩前端(弯曲激波封口点)点竖直向下投影至壁面点，便是唇口截面，便为基于壁面马赫数分布规律求解得到的压缩型面。至此便完成了进气道外压段的曲压缩面设计以及相应的流场求解。

图6 特征线法求解过程(基于壁面马赫数分布)Fig.6 Schematic of characteristic line solution (based on Mach number distribution)

1.2 内压段及隔离段设计

在内压段型线设计中，需要将经过外压段压缩流向发生偏转的气流继续压缩，且重新引导至水平方向，同时尽可能使喉道截面处的主流区速度分布均匀。如图7所示，内压段肩部型线的设计采用圆弧进行光顺过渡，唇罩压缩面的设计采用二阶贝塞尔曲线。二阶贝塞尔曲线路径上任意一点由给定点、、的函数()追踪(如式(14)所示)，通过调整点的位置，即可控制唇罩起始压缩角的大小、唇罩反射激波的强度以及唇罩激波反射点的位置，从而避免下壁气流在过大的逆压力梯度下分离。喉道截面处上下壁面均保持水平，且通道面积变化率为零，考虑到进气道在实际工况下的起动问题，喉道高度的取值参考KANTROWITZ等极限起动判据给出。隔离段采用等直隔离段设计，为获得较好的隔离段出口性能及承受反压能力，隔离段长度参考文献[28]中针对等直隔离段的相关研究给出。

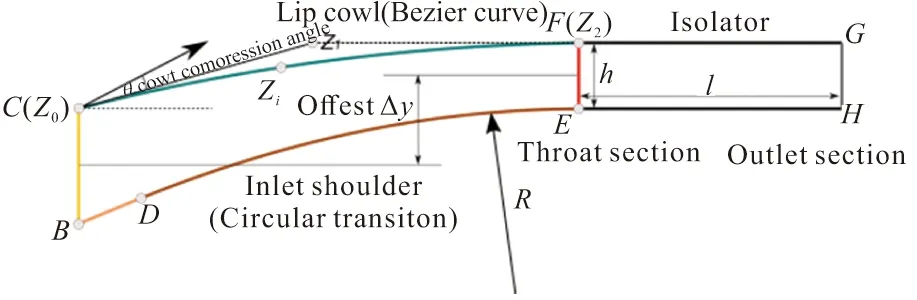
图7 进气道内压段及隔离段设计Fig.7 Schematic of inlet internal pressure and isolation section design

()=(1-)+2(1-)+,∈[0,1]

(14)

在给定喉道偏距的Δ(喉道截面中心与外压段出口截面中心的偏距)、喉道高度、圆弧半径及隔离段长度后，即可设计出相应的内通道几何型线。

2 进气道流场快速求解方法

2.1 设计点流场求解

在设计点工况下，进气道外压段型线是根据流线追踪得到。因此，在完成外压缩型面逆设计的同时，也即完成了相应的外压段流场求解；而对于进气道内通道的流场求解，则依赖图6中唇口截面的参数分布以及内通道型线的几何分布。具体的求解思路为运用有旋特征线法对通道内点、壁面点以及通道内激波点依次求解，其中壁面点单元求解和内点单元求解在文献[29]和文献[30]中有详细介绍。本节主要介绍唇罩激波及通道内反射激波系的求解方法。

如图8所示，根据外压段求解得到的截面的气动参数和肩部型线的几何坐标，采用内点单元求解过程及壁面点单元求解过程，可解得入口截面和内通道下壁面共同作用下的影响域(粉色区域)。在此基础上，考虑唇罩激波起始点处的流场结构，内压段入口气流在唇罩的强压缩作用下产生局部斜激波，然后不断向下游传递，最后终止于内通道下壁面点，从而形成流道内的唇罩激波。因此，在影响域求解完成的基础上，内通道的唇罩激波形状完全依赖于唇罩的几何构型，且唇罩激波起始段的求解精度会影响整个通道内唇罩激波的求解精度。

图8 进气道唇罩激波求解示意图Fig.8 Schematic of inlet lip cowl shockwave solution

考虑问题的一般性，以图9中的1点、2点分别代替图8中的点和唇罩壁面上点。在已知1点的位置坐标(,)、波后气流参数(,,,,)和2点位置坐标(,)的情况下，激波起始段13的求解需要通过双层循环迭代完成，其中内层循环用来确定3点信息，然后通过外层循环迭代更新2点气流参数，当2点气流参数收敛后完成求解。具体求解步骤如图10所示。

图9 唇罩激波点求解过程Fig.9 Schematic of lip cowl shockwave point solution

图10 激波起始段求解步骤Fig.10 Schematic diagram of the solution of the shock start segment

在完成唇罩激波起始段的求解之后。沿壁面发出的右行特征线和唇罩激波发出的左行特征线交替向下游求解至唇罩激波与下壁面的交点发出的结尾左行特征线(如图8所示)。在此期间，多次运用壁面点单元、内点单元以及激波点单元求解过程，即可确定区域--内的流场参数。此外，在流场计算的步进过程中，若某区域需要加密计算，可以适当增加计算网格点。同理，按照上述计算方法可完成通道内反射激波系的求解，当求解至进气道出口截面时，即完成了内通道流场的求解。

2.2 非设计点流场求解

在给定高超声速进气道的设计指标和几何约束后，通过上文介绍的型面设计及流场求解方法进行多次迭代求解，可获得进气道的几何型面。当飞行工况处于非设计点时，首先根据非设计点来流条件完成进气道外压段的流场求解。如图11所示，在亚额定工况中，进气道前缘弯曲激波将不会封口于唇罩处。因此，在型面和激波间沿特征线推进求解，求解区域能够包含唇口截面。在获得唇口截面的气流参数分布以后，根据2.1节中的内通道流场求解方法，可完成亚额定工况下进气道流场求解。

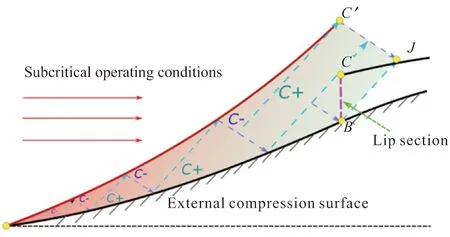
图11 亚额定工况下进气道流场求解Fig.11 Solution of inlet flow field under sub- standard operating conditions

在超额定工况中，前缘弯曲激波直接打入内压段与唇罩相交，通过外流场的求解无法全部获得截面的气流参数分布。因此，内通道流场求解方法不再适用，故本文仅对进气道的亚额定工况流场求解进行讨论。

3 方法验证

3.1 典型进气道构型设计

根据上文所述的进气道构型设计及流场计算方法，以=6、=30 km为设计点(表示飞行高度)，在几何约束给定的前提下，以出口总压恢复及出口马赫数为优化指标，完成图12所示的高超声速弯曲激波压缩进气道构型的初步无粘设计。主要设计参数如表1所示。

图12 亚额定工况下进气道流场求解Fig.12 Solution of inlet flow field under sub-standard operating conditions

表1 典型高超声速进气道主要设计参数Table 1 Main design parameters of Hypersonic inlet

3.2 无粘流场求解及精度验证

针对图12所示构型运用本文流场快速求解方法(MOC)进行求解，其中外压段流场边界约束相对较少，沿特征线的推进求解相对容易。内压段流场中存在唇罩激波、肩部膨胀区以及反射激波等多种复杂流场结构，求解边界约束较多，需要在内通道壁面及通道内激波间沿特征线反复推进求解。因此，在保证计算精度和准确性的前提下，从流场快速准确求解角度出发，本文选用100个节点来离散前缘弯曲激波，并在内压段入口截面段布置120个计算节点来保证内通道流场求解精度。进气道内压段的计算节点如图13所示。

图13 内压段计算节点分布(MOC)Fig.13 Node distribution of MOC in the internal compression segment

图14为MOC方法求解得到的进气道无粘流场压比云图(选用来流静压进行无量纲化处理)以及马赫数云图。从图14中可以看出，本文的流场快速求解方法能够很好的捕捉到进气道流场内的波系结构。在求解效率方面，在进气道构型相同的前提下，CFD方法从前处理网格划分到求解完成平均耗时约20min，而本文MOC方法平均耗时约4 s，与CFD方法相比，求解效率提升300倍左右。此外，依据本文MOC方法还可进行进气道无粘性能的快速评估，与进气道型面设计方法结合后，能够有效缩短进气道设计迭代周期。

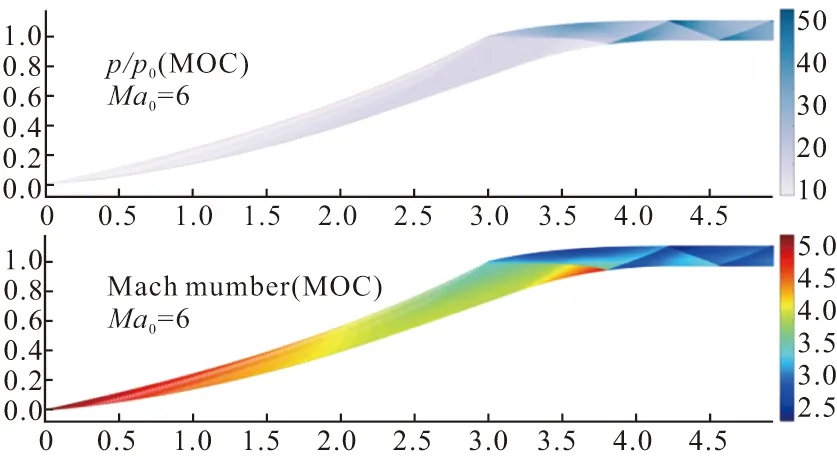
图14 无粘流场压比云图及马赫数云图(MOC)Fig.14 Pressure ratio contour and Mach number contour of inviscid flow field(MOC)

为验证上述无粘流场快速求解方法的计算精度，选用CFD无粘数值仿真结果进行对比验证。CFD仿真基于有限体积法的密度基求解器完成，其中对流通量的插值计算采用二阶迎风Roe格式，时间推进采用隐式LU-SGS方法。当计算残差收敛至1×10以下时求解完成。CFD仿真中使用的计算网格及边界条件设置如图15所示，网格量约25 000。设计工况下的CFD仿真结果如图16所示。

图15 网格划分及边界条件设置(CFD)Fig.15 Mesh division and boundary conditions

对比图14和图16可以看出，本文采用MOC方法计算得到的进气道流场参数分布与CFD结果十分符合。同理，分别采用CFD方法和MOC方法对亚额定工况=5和=4°条件下的进气道流场进行计算(表示攻角)，得到图17、图18中所示的压比参数分布云图，从图中可以发现，在亚额定工况下，MOC结果和CFD结果同样吻合较好。

图16 无粘流场压比云图及马赫数云图(CFD)Fig.16 Pressure ratio contour and Mach number contour of inviscid flow field(CFD)

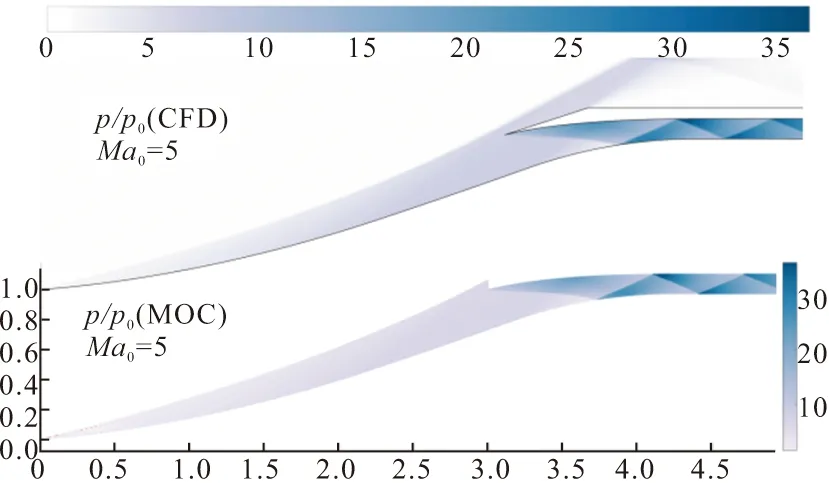
图17 亚额定工况下压比云图对比(CFD&MOC,Ma0=5)Fig.17 Comparison of pressure ratio contours under sub- standard operating condition(CFD&MOC,Ma0=5)

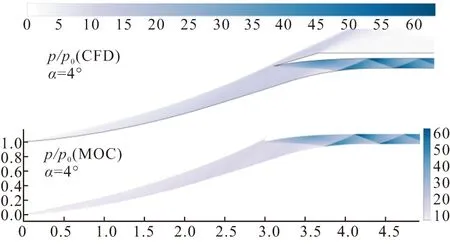
图18 亚额定工况下压比云图对比(CFD&MOC,α=4°)Fig.18 Comparison of pressure ratio contours under sub- standard operating condition(CFD&MOC,α=4°)

为了更加直观地验证本文提出的流场快速求解方法的准确性，选取上述设计工况=6、亚额定工况=5以及=4°条件下的进气道下壁面压比分布作对比校验。如图19所示，使用特征线法计算得到的壁面沿程压力分布与CFD计算结果完全吻合，沿程的压力阶跃位置也与CFD计算结果符合较好，表明本文的快速流场计算方法能够精确地捕捉到通道内的唇罩激波及激波反射点的位置。此外，从图19(b)中可发现，MOC方法计算得到的激波前后压升幅度更大，峰值区域也更为尖锐，而CFD计算得到的压力峰值区域更为光滑，这主要是由CFD方法中网格尺度和对流通量格式人工耗散导致的。一方面，网格尺度问题会导致CFD方法对激波的捕捉精度下降；另一方面，对流通量格式在激波附近降为1阶精度，导致耗散增加，从而使得CFD捕捉到的激波存在一定量宽度。而特征线法在激波位置判断上不存在宽度，因此CFD方法得到的压力阶跃位置相比MOC方法得到的压力阶跃位置存在滞后性，这与文献[26]的结论一致，表明特征线法的计算结果可更好地对内通道无粘流场进行模拟。

(a)0

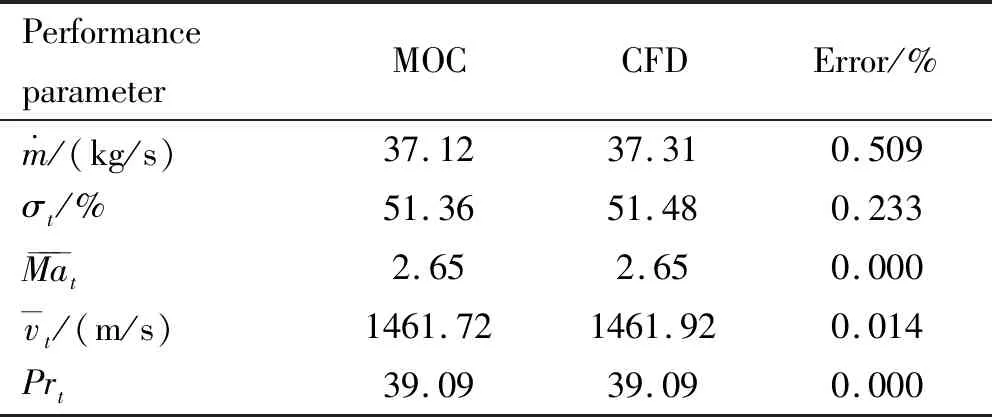
3.3 无粘性能精度验证

(15)

(16)

式中为不同的进气道截面，为0时表示来流远场截面，为时表示进气道喉道截面，为1时表示进气道出口截面；为气流与当前进气道截面的夹角；、、、、分别为气流密度、压力、速度、总压、马赫数；d为当前截面的积分线元。

表2给出了设计点工况下，基于MOC方法与基于CFD方法的进气道喉道截面性能参数对比。从表2中可以看出，基于本文MOC方法得到的喉道性能与CFD无粘仿真结果相近,最大误差小于2%。其中，截面流量和增压比的误差相对较大，这主要是因为在高马赫数条件下，进气道对气流的增压作用较强，喉道处气流的绝对压力值较高，导致计算误差在内通道流场推进求解过程中不断累积，并且不易消除，从而在喉道截面性能中呈现出相对较大的压力误差和流量误差。

表2 设计工况下进气道喉道性能对比(MOC&CFD)Table 2 Comparison of throat section performance parameters at design point(MOC&CFD)

参照设计点性能对比，亚额定工况=5以及=4°条件下的进气道性能对比由表3以及表4给出。从中同样可以看出，基于本文MOC方法和基于CFD方法得到的截面性能符合较好，最大截面性能误差小于2%。

表3 亚额定工况下进气道喉道性能对比(MOC&CFD,Ma0=5)Table 3 Comparison of throat section performance under sub- standard operating condition(MOC&CFD,Ma0=5)

表4 亚额定工况下进气道喉道性能对比(MOC&CFD,α=4°)Table 4 Comparison of throat section performance under sub- standard operating condition(MOC&CFD,α=4°)

4 结论

(1)将基于激波形状的型面逆设计方法与基于壁面参数分布规律的型面逆设计方法相结合，给出了一种兼顾几何约束与气动需求的进气道参数化设计方法，该方法型面控制参数简单，物理含义明确，可实现几何和气动兼容下的进气道型面快速设计。

(2)提出了一种基于有旋特征线法的高超声速进气道流场快速求解方法(MOC)，可对前缘弯曲激波、唇罩激波、肩部膨胀区以及激波反射等流场进行准确捕捉求解，实现了对高超声速进气道设计与亚额定工况下流场的快速求解。与无粘CFD方法相比，本文MOC方法求解效率提升300倍左右，喉道截面性能参数求解误差不超过2%。

(3)将高超声速进气道快速设计及型面快速求解方法相结合，在获取进气道设计方案的同时，可快速获取进气道不同工况下的无粘气动性能，也可为进气道自动优化设计提供支撑。