基于坐标融合的大型壳体壁厚自动测量方法研究
吴 桐,高 越,刘 柯,郭力振,鲍晨兴,孙增玉
(北京航天计量测试技术研究所,北京 100076)
1 引 言
大型薄壁柱段壳体为箭体典型结构件,其结构特点为:尺寸大,高度不等;结构复杂,采用上、下端框加中间内网格柱段结构,其中,上、下端框结构不对称,尺寸不等,内形网格蒙皮厚度不等,筋宽不等,网格、凸台大小及分布位置不均,窗口及下陷大小不等,且位置呈不对称分布;尺寸精度高,网格蒙皮壁厚精度要求为±0.20 mm。 壳体网格蒙皮壁厚是设计关键尺寸之一,传统的壁厚测量方法包括手动弓形量具壁厚测量法、三坐标壁厚测量法和超声波壁厚测量法,如图1 所示。

图1 传统壁厚测量方法Fig.1 Conventional wall thickness measurement methods
采用弓形量具壁厚测量法测量时,需要两位检验员在壳体内外配合测量,完成数百个网格测量工作需要约1 ~2 天,检验人员劳动强度较大,而且,测量精度依赖百分表法向位置,需双人协作,精度较低,一致性较差;采用三坐标测量机测量,虽然单点坐标测量精度高,但单点式测量点云密度低,形面特征拟合精度低,测量效率低,自动化测量耗时约1天,由于此类产品数量较大,势必会长时间占用坐标测量机,影响其它型号产品的正常生产;目前主要采用手持式超声波测厚仪,由检验人员逐格、逐点测量,单点测量动作包括涂耦合剂、测量、读数、记录,完成一件产品的网格壁厚测量耗时约1 天,而现场一般两人同时配合,分别负责检验和记录,劳动强度同样比较大,同时,在测量前需要针对不同材料制作标准试块,且材料内部缺陷和手持测头的法向控制手法对测量结果准确度都会产生影响。
本文针对壳体类产品尺寸的批量、高精度、快速测量需求,设计了一套基于机器人的光学三维扫描测量系统。 该测量系统可以自动快速获取壳体外形轮廓三维点云数据,通过坐标标定与数据融合,无需外部拼接参考标志点即可实现零件不同部位三维点云数据的高精度拼接,建立高精度零件整体外形轮廓三维点云模型,并在软件中对其壁厚等尺寸进行分析计算,并生成测量报告,有效缩短测量时间,提高了测量效率。
2 机器人光学三维扫描测量原理
机器人光学三维扫描测量系统主要由六自由度工业机器人、光学扫描测头、定位转台、控制柜、工作站、数据处理及解算分析软件等组成,如图2所示。 其中,光学扫描测头由激光投影仪与立体视觉相机组成。 光学扫描测头固定在机器人第六轴法兰末端,激光投影仪在壳体表面投射光栅条纹,立体相机拍摄条纹图案并通过相位解算,以点云方式获取壳体轮廓坐标数据;工业机器人搭载扫描测头,代替人手实现扫描测头的快速、精确定位;精密定位转台搭载被测壳体,将壳体不同象限区域辅助定位到扫描测头同一测量站位。 转台与机器人联动,不仅能有效扩展机器人的作用范围,还能减少机器人运动次数,提高测量效率;测量系统在软件支持下基于壳体设计模型自动生成扫描路径,并完成壳体内外轮廓遍历扫描;扫描结束后使用数据处理及解算分析软件,基于壳体设计模型进行点云坐标数据的形位误差分析,并自动生成检测报告。

图2 机器人光学三维扫描测量系统组成示意图Fig.2 Composition diagram of robot optical three⁃dimensional scanning measurement system
光学扫描测头的单场检测范围有限,无法只通过一次扫描建立壳体内外轮廓整体点云模型,需要扫描测头变化不同位置和角度进行多站位扫描,并将测头不同站位下的扫描测量数据进行拼接。 传统的多站位扫描数据拼接方法为:利用外部双目光学跟踪器实时跟踪光学测头,采集测头位姿坐标,将测头不同站位的位姿坐标统一到固定不动的跟踪器世界坐标系中,实现多站位扫描数据拼接。 但采用该方法测量壳体内部时,由于遮挡导致跟踪器无法追踪测头;此外,在零件表面或者专用测量工装表面粘贴参考标志点,在标志点建立的全局控制场的基础上实现多站位扫描数据拼接,虽然该方法拼接误差不受拼接次数的影响,但是贴点和控制场标定过程复杂,无法满足批量零件的快速检测需求。
将多坐标系测量系统进行坐标精密综合标定,实现坐标统一。 自动化扫描测量过程中,无论是调整测头位姿,还是旋转被测壳体,都可以将每次测量数据转换到一固定的世界坐标系中,以此实现多站位扫描数据的拼接。 此外,坐标统一也是实现基于壳体CAD 设计模型扫描路径自动规划与路径虚拟仿真的前提条件。
3 测量系统坐标系标定与统一
测量系统坐标系包括扫描测头坐标系K、壳体轮廓测量点云坐标系K、自定位转台坐标系K和机器人世界坐标系K,如图3 所示。 为了完整地描述被测对象的几何特性,必须把测头各个位置下的测量数据统一到固定坐标系中,为了实现坐标统一,需通过坐标标定获得各个坐标系之间的转化关系,即旋转变换矩阵M。
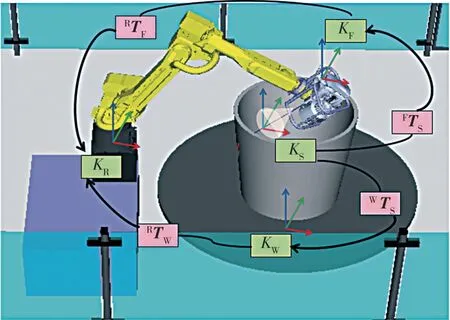
图3 机器人光学三维扫描测量系统坐标系组成及转换示意图Fig.3 Schematic diagram of coordinate system composition and transformation of robot optical three⁃dimensional scanning measurement system
K由机器人本体结构决定,本文三维扫描测量系统置于地面固定后,K相对于大地固定不动,因此可将其作为固定坐标系。 将测头各站位测量数据转换到K中,以此实现多站位测量数据的坐标统一,即数据拼接。 数据拼接模型为

式中:T——K与K的转换矩阵;T——K与K的转换矩阵;T——K与 K的转换矩阵;T——K与K的转换矩阵。
所有转换矩阵都为4 ×4 矩阵,可由旋转矩阵R和平移向量T表示为

3.1 壳体点云坐标系KS 与转台坐标系KW 的标定
被测壳体轮廓三维点云数据反映的是真实的零件外形,一旦被测壳体被固定在转台台面上,则T即被唯一确定。 实际测量过程中,通过定位销与定位销孔,实现被测壳体与转台台面的同心精确定位,并通过压紧装置防止测量过程中壳体与台面发生相对窜动。 因此,可认为K与K重合,即T=1。 若被测零件为非回转体结构,或者零件回转轴线与转台回转轴线不重合,则T≠1,具体值可由三维设计软件计算获取。
3.2 转台坐标系KW 与机器人世界坐标系KR 的标定
本文利用激光跟踪仪作为测量装置完成K与K的标定。 标定方法为:
(1)利用水平气泡,精密调平定位转台;
(2)在靠近定位转台台面边缘的位置固定一个直径3.81 cm(1.5 in)的靶球;
(3)转台回零后,激光跟踪仪测量第一个点的三维坐标值,如图4 所示;
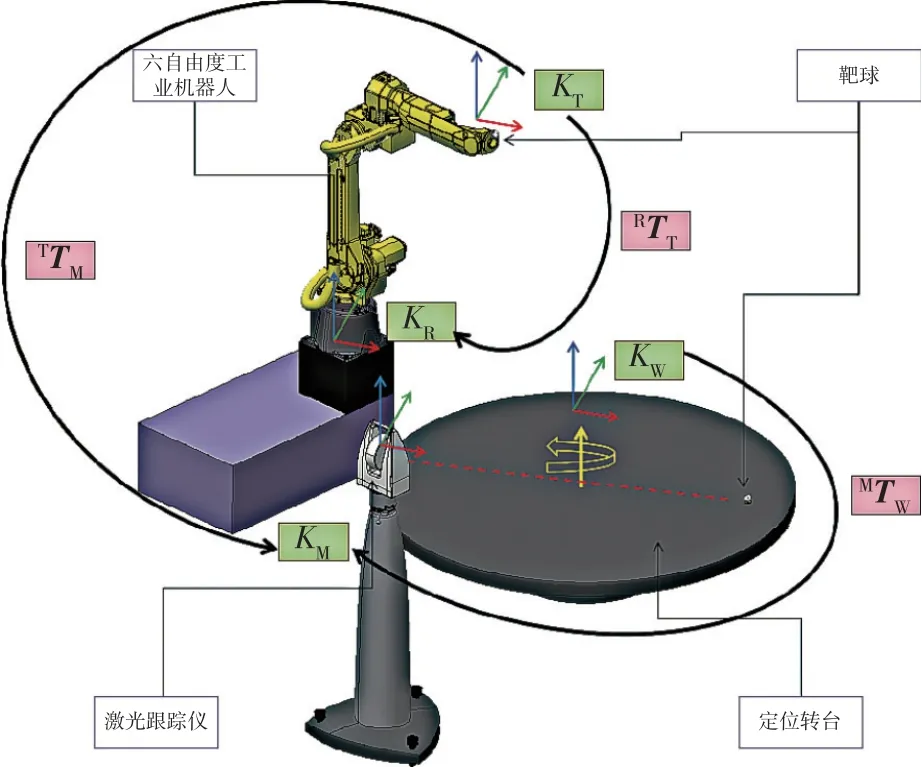
图4 转台坐标系标定示意图Fig.4 Shematic diagram of turntable coordinate system calibration
(4)控制转台每旋转30°静止后,测量靶球中心点的三维坐标P(x,y,z),其中,i =1,2,…,12;利用最小二乘法将测量的12 个点拟合成空间圆。

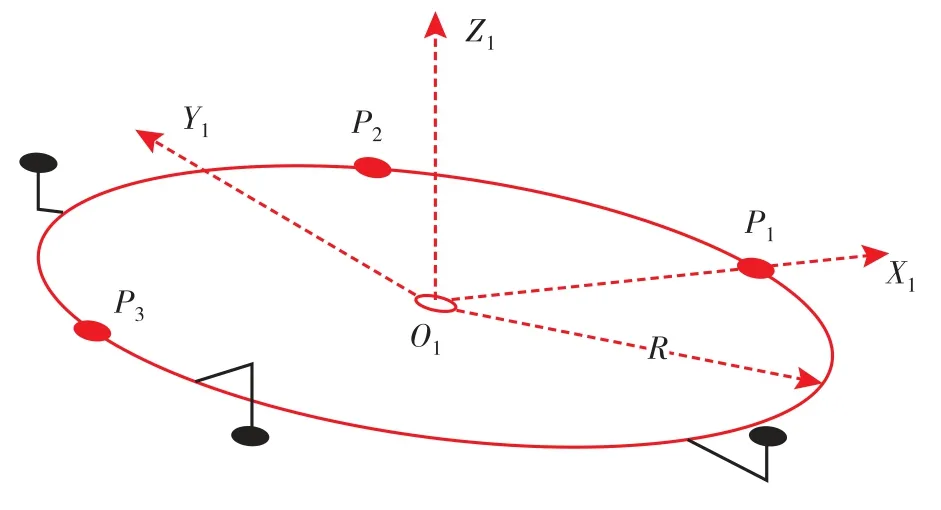
图5 转台坐标系建立示意图Fig.5 Schematic diagram of turntable coordinate system establishment
(5)激光跟踪仪位置保持不动,机器人末端第六轴法兰面边缘位置固定一个直径3.81 cm(1.5 in)的靶球;
(6)机器人所有运动轴回零后,激光跟踪仪测量第一个点的三维坐标值,如图6 所示;
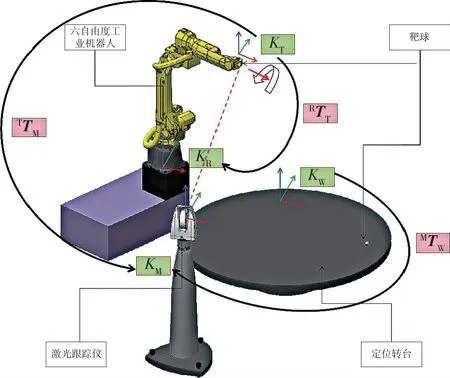
图6 机器人工具坐标系标定示意图Fig.6 Schematic diagram of robot tool coordinate system calibration
(7)控制机器人末端第六轴每旋转30°静止后,测量靶球中心点的三维坐标Q(x,y,z),其中,i =1,2,…,12。


图7 机器人工具坐标系建立示意图Fig.7 Schematic diagram of robot tool coordinate system establishment
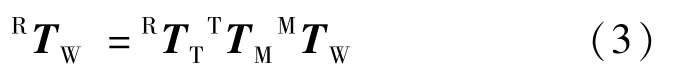
3.3 壳体点云坐标系KS 与扫描测头坐标系KF 的标定
利用专用标定板,对扫描测头的双目视觉测量单元进行标定获取CCD 相机的内、外参数,对光栅投影测量单元进行标定获取像素坐标与世界坐标的关系,扫描测头的标定技术和方法已经相当成熟,本文不再赘述,通过对扫描测头的综合标定计算得到K与K的转换矩阵T。
3.4 扫描测头坐标系KF 与机器人世界坐标系KR标定
本文采用“手—眼”标定法,标定计算K与K的转换矩阵T,所使用的标定物体为不规则多面体,如图8 所示,以其中四个面为测量面,标定流程为:
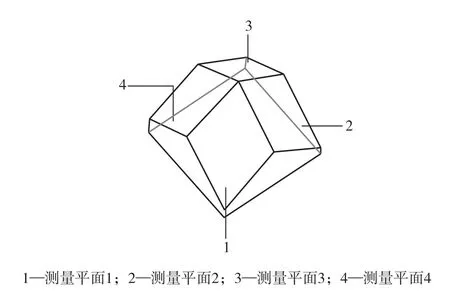
图8 不规则多同体结构示意图Fig.8 Schematic diagram of irregular polyhedron structure
(1)使用机器人示教器,手动调节扫描测头与对齐块的空间位置,测量对齐块,通过相位解算,得到站位1 下对齐块测量点云数据;
(2)对齐块位置不变,扫描测头变化位置,测量对齐块,同理得到站位2 下对齐块测量点云数据;
(3)C表示对齐块坐标系,K和K分别表示站位1、站位2 下扫描测头坐标系。 根据3.3 节的标定结果和第(2)、(3)步的测量数据,可以分别得到K、K与C的转换矩阵,用A 和B 表示。 可通过对齐块特征点云数据的最佳拟合,得到K与K的相对位姿关系,用T 表示,则
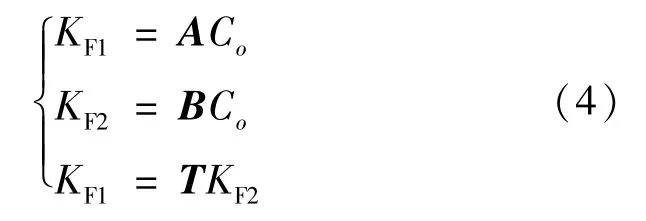
(4)K和K分别表示扫描测头站位1、站位2下机器人工具坐标系,由机器人示教器面板读数,可计算得到K和K的转换矩阵,用F 表示,则

(5)用T表示K与K的转换矩阵,由于扫描测头固定在机器人末端的法兰上,因此K与K,K与K之间的转换矩阵都为T,则

由公式(4)~(6),得TT =FT,其中,T 和F已知,即可求得T,T为4 ×4 矩阵,由旋转矩阵R和平移向量矩阵T组成,即

则

其中,T为K与K的转换矩阵,可由机器人示教器控制面板读出。
通过第3.1 ~3.4 节的坐标标定过程,实现了机器人光学三维扫描测量系统各个坐标系的统一,测量过程中,测量系统采集到的K可实时转换到固定的K下,完成多站扫描测量数据的高精度拼接。
4 壳体自动化测量应用
4.1 测量结果及数据分析
利用机器人光学三维扫描测量系统,对某型号锥形壳体进行了测量试验,通过点云数据拼接和封装处理,得到被测产品的三角网格测量模型,如图9所示。
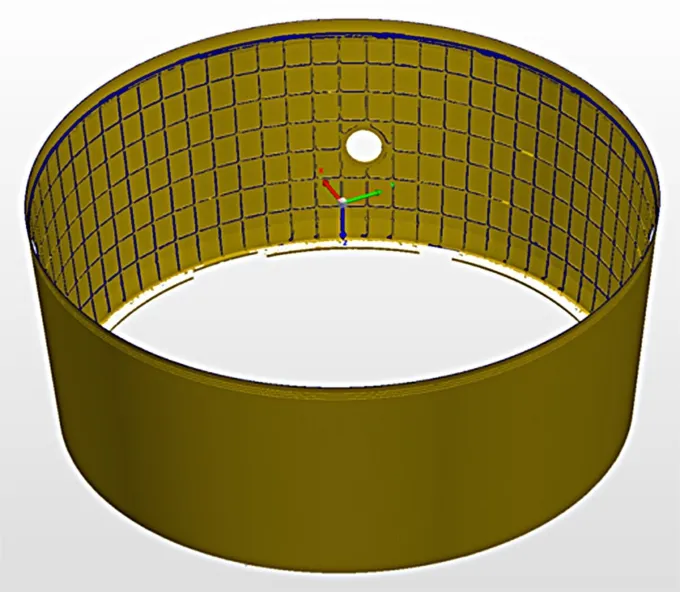
图9 锥形壳体测量三角网格模型Fig.9 Triangular mesh model of conical shell measurement
在Polyworks 软件中,以色差彩图的形式直观地表征零件的整体加工壁厚分布,如图10 所示,可通过壁厚彩图快速检查零件实际壁厚分布情况,也可检测指定点的壁厚值。
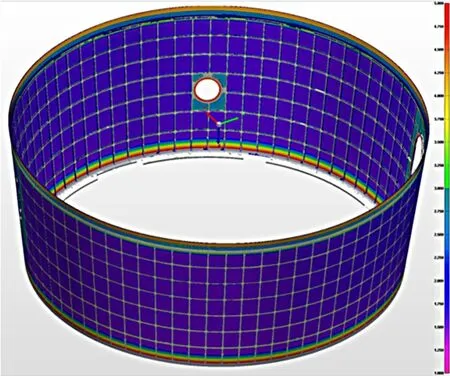
图10 锥形壳体壁厚检测彩图Fig.10 Color map of thickness distribution of conical shell
对锥形壳体进行6 次重复扫描测量试验,解算得到产品的三维网格模型,基于此模型,自动解算488 个栅格中心位置6 次重复测量的壁厚值,并与计量型三坐标测量机测得的壁厚值进行比较,所有壁厚值偏差≤±0.05 mm,测量数据见表1。
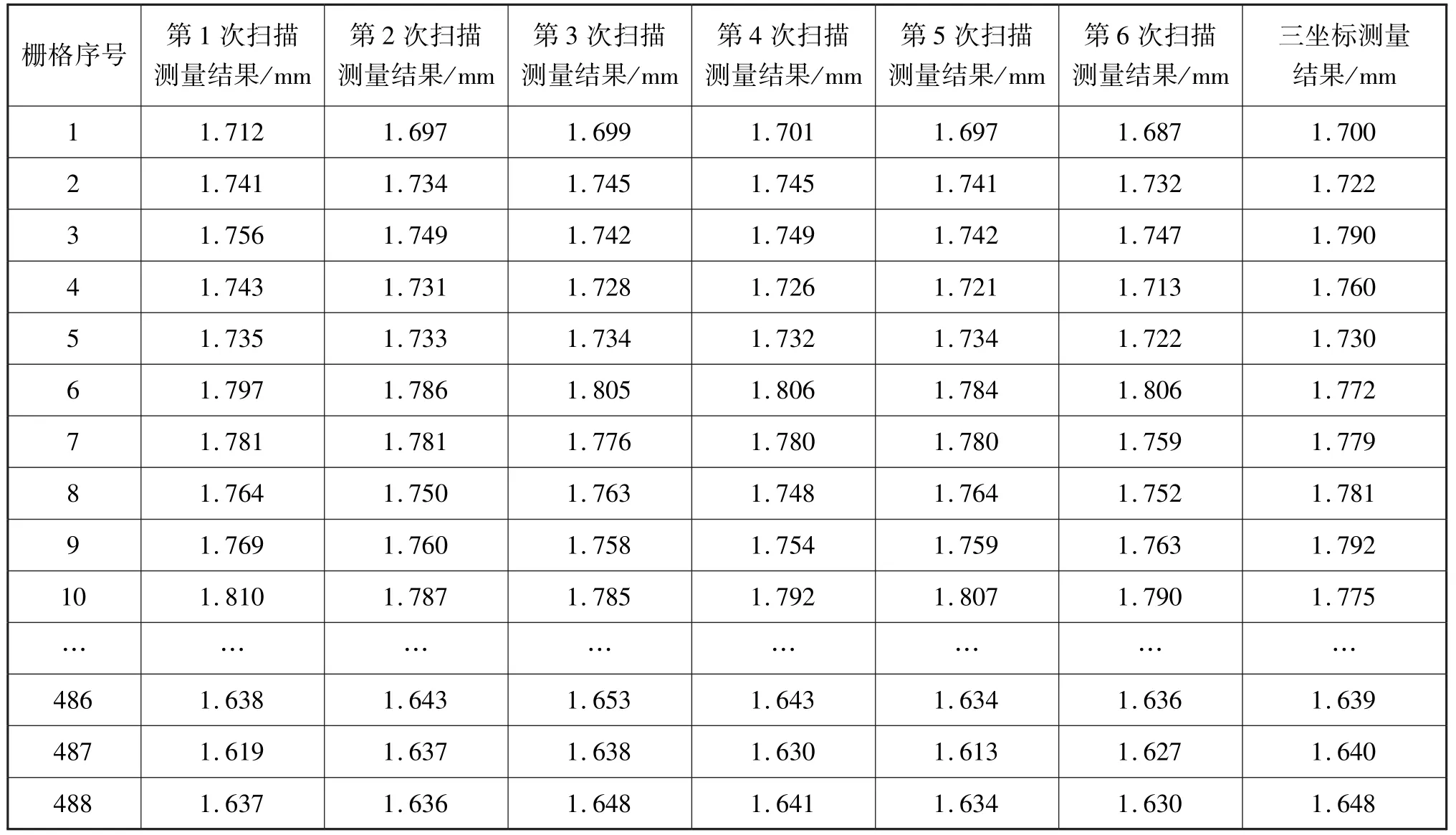
表1 锥形壳体重复扫描测量壁厚值与三坐标测量壁厚值Tab.1 Wall thickness measured of conical shell by epeated scanning measurement and three coordinate measurement
利用贝塞尔公式(9)计算每个位置壁厚实测值的标准偏差s(A),壁厚实测值标准偏差统计结果见表2。
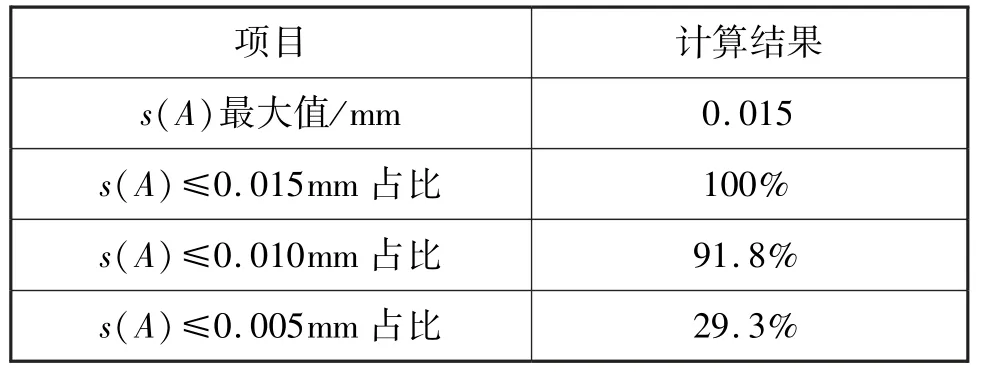
表2 锥形壳体重复测量壁厚实测值标准偏差统计结果Tab.2 Statistical results of standard deviation of measured values of repeated thickness measurement of conical shell
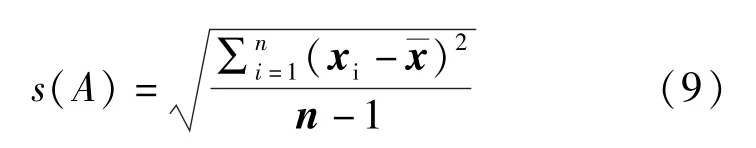
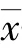
4.2 测量不确定度分析与评定
按照《JJF 1059.1-2012 测量不确定度评定与表示》的要求,对测量系统的壁厚测量不确定度进行分析评定。
4.2.1 测量模型
由测量原理和方法,得到测量模型,

式中:e——第i 次测量壁厚误差,mm;x——第i 次测量壁厚值,mm;d——第i 次测量壁厚标准值,mm。
4.2.2 标准不确定度分量来源和说明
标准不确定度分量来源和类别见表3。

表3 标准不确定度分量来源和分类Tab.3 Source and description of standard uncertainty component
4.2.3 标准不确定度分量计算
(1)机器人光学三维扫描测量系统测量不确定度引入的不确定度分量u
根据机器人光学三维扫描测量系统校准证书,测量系统测量不确定度U =0.01 mm +1.5 ×10L(k =2),按B 类不确定度处理,则
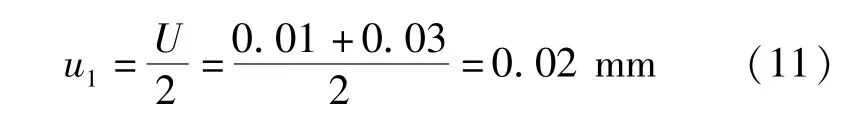
(2)测量重复性引入的标准不确定度分量u

由表2 可知,s(A)=0.015 mm,因此,
u=0.015 mm
(3)合成不确定度u
测量系统的壁厚测量合成标准不确定度u按公式(13)计算。
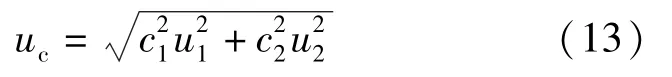
式中:c,c——灵敏系数,c=1,c=1,因此,

(4)扩展不确定度U
测量系统的壁厚测量扩展不确定度U 按公式(14)计算,k =2,
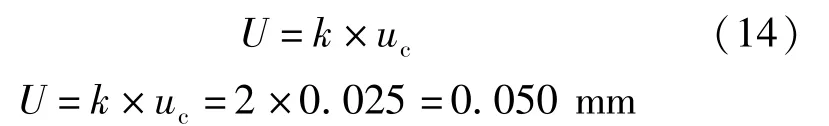
5 结束语
通过对基于坐标融合的大型壳体类零件壁厚光学测量方法的研究,实现了大尺寸壳体类零件壁厚的自动化扫描测量,与多站位扫描测量数据的高精度拼接。 研究表明,测量系统对壳体壁厚的测量不确定度≤0.05 mm,满足壁厚尺寸的测量要求;此外,自动化测量代替手工检测,将检测时间由原来的两人工作24 h 缩短到现在的1.5 h,检测效率显著提高,降低了检测人员的劳动强度,且易于实现规范化检测,避免了检测结果因人而异、重复性差等负面影响,提升了产品的检测水平。

