基于UKF的FADS/INS融合大气数据估计
蒋保睿,刘 鹏,肖地波
(成都信息工程大学控制工程学院,成都 610225)
1 引 言
对于高速飞行器而言,大气数据包括空速(V)、攻角(α)、侧滑角(β)、总压(q)、静压(p)等参数,其测量精度和可靠性影响飞行器控制系统的正常工作及性能发挥,关系到飞行安全和质量。目前普遍使用探针传感技术测量大气数据,凸出的空速管和风向标不仅在高速飞行时测量数据不够准确,还会影响飞行器的机动和隐身性能。 为了解决上述问题,人们开始寻找更为可靠的测量方法。嵌入式大气数据传感系统(Flush Air Data Sensing System,FADS)采用嵌入在飞行器前端不同位置上的压力传感器阵列测量飞行器表面的压力分布,根据测得的压力值,按照一定的算法解算得到大气数据。美国Dryden 飞行研究中心在20 世纪60年代开始对FADS 进行研究,在理论上证明了该系统可满足现代飞行器对飞行速度、机动性等方面的要求。
惯性导航系统(Inertial Navigation System,INS)短时间的导航精确度高于FADS,但其突出缺点是受到漂移误差影响,导航的精度随时间的增长而降低。 为解决这些问题,将大气数据系统、惯导系统组合使用是较为常见的一种方式。 上世纪末,FADS 被首次应用在飞行器上,标志着系统的可行性;近年来,陆辰等人提出了一种基于FADS 的扩展卡尔曼滤波(Extended Kalman Filtering,EKF)实时估计大气参数的方法,验证了大气数据系统的测量范围和可靠性;Karlgaard 等人在研究火星探测器着陆阶段的空气数据估计时,使用全状态(速度和姿态)惯性量的辅助,与原有的大气数据处理算法相比,精度得到了提升。
为了提升算法在复杂飞行状态时对参数的估计能力、进一步降低误差,本文提出一种基于无迹卡尔曼滤波(Unscented Kalman Filtering,UKF)的大气数据和全状态惯导数据估算真空速、攻角和侧滑角的方法。 该方法利用INS 测量惯性数据,同时FADS 测量大气数据,最后通过UKF 滤波,解算出精度更高的攻角、侧滑角、真空速等大气参数。 另外,本文FADS 解算部分提出了一个快速求解动静压的方法,在减少迭代步骤、提高计算速度上取得了良好的效果。
2 系统设计
基于UKF 的FADS/INS 融合大气数据估计系统包括惯性导航系统、用于测量气压值的FADS 系统和信息融合估计算法。 本章介绍惯导系统和FADS 的数据解算、UKF 滤波算法以及根据滤波输出值求解大气数据的方法。
2.1 惯导系统数据解算
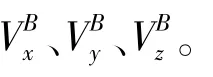
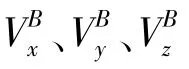
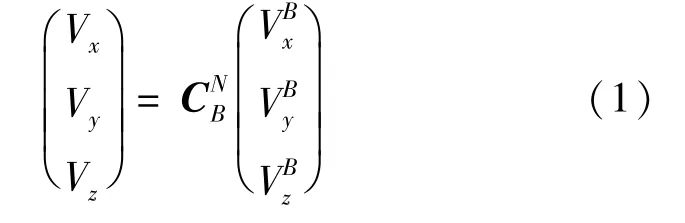
其中,旋转矩阵的值完全由当前时刻的姿态角决定,求解公式为

2.2 FADS 模型解算
FADS 通过飞行器表面特定区域的压力分布反推得到飞行参数,解算顺序一般为:动静压、攻角侧滑角、马赫数和气压高度。
已知测压孔的位置参数和每个孔的压力值,可列写如下方程求解动静压:

式中:σ——第i 个孔对应的气流方向,p——第i 个测压孔在当前时刻所测压力,f——一个单调增函数,其自变量为动静压之比,因变量为修正系数,用于修正不同马赫数下测压孔数据,可由实验或牛顿理论确定。 当孔的数量为5 时,式中n =5,即用五个方程组成的方程组求解动压q与静压P两个未知数。 如果直接利用计算机求数值解,不仅耗时长、计算繁琐,而且精度不高。 利用伪逆,公式(3)可化简为

经迭代即可求解q与P,经测试,在结果精度相同的情况下,改进算法的运行时长比原算法减少约70%。
分别选择竖直对称轴和水平对称轴的三个测压孔数据,得到局部攻角与局部侧滑角,具体表达式为
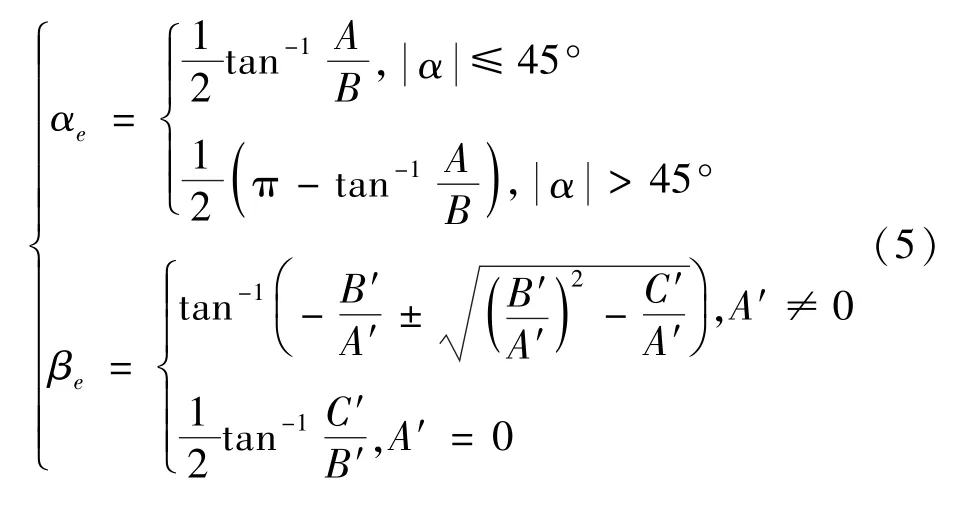
其中,A、B 用于求解攻角,利用垂直的测压孔数据,与竖直分布的测压孔数据有关;同理A′、B′、C′用于求解侧滑角,与水平分布的测压孔数据有关。
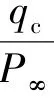

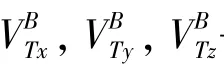
2.3 UKF 方程设计
在适用于非线性系统的改进卡尔曼滤波算法中,常用方法有EKF 和UKF。 相较于EKF,UKF 采用无迹变换(Unscented Transformation,UT),在状态预测时采用非线性传播方式,避免了EKF 在使用线性逼近非线性变换时的截断误差,滤波结果更加准确,且避免了繁琐的雅克比求解工作。
选取飞机的真空速、加速度、姿态角、姿态角角速度作为状态量,即
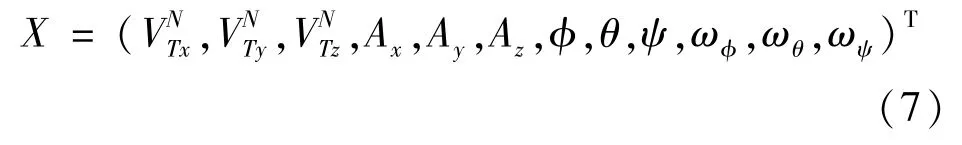

因为大气紊流的时间短、速度及其改变量小,
所以可以认为地速与真空速的加速度一致,即
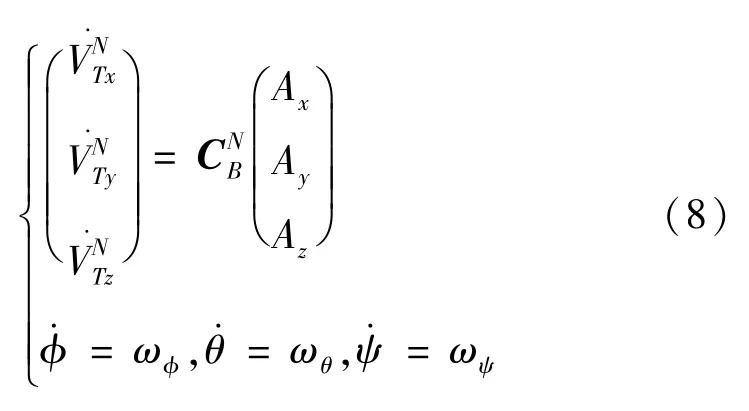
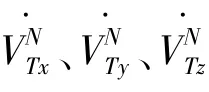
经整理可得状态方程
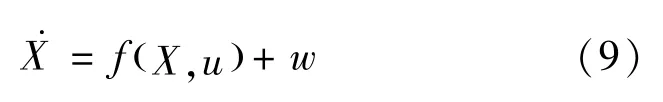
式中:u =(A,A,A,ω,ω,ω)——输入量;w——系统噪声向量。
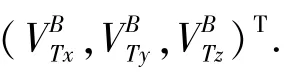
由公式(4) ~公式(8)可得真空速V、攻角α、侧滑角β,基于此三个大气数据,按公式(6)求得地面坐标系下的空速分量,即观测方程为

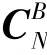
2.4 滤波计算
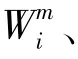

其中,a 的选择控制了采样点的分布,通常取一个不大于1 的正数,此处取0.2;b 是一个非负的权系数,对于高斯分布,可以从理论上证明b =2 是最优的;n 为维数,根据系统状态量X 的形式,此处取n =12;λ =n(a-1)。
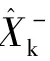
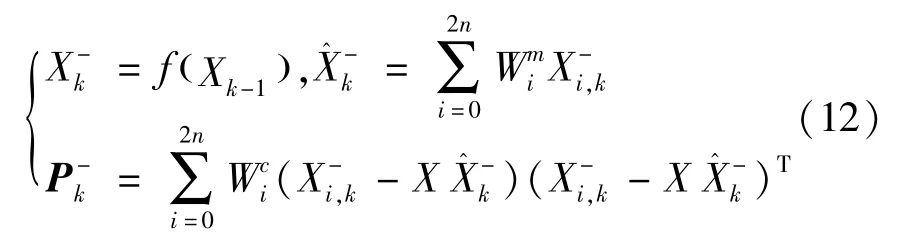
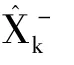
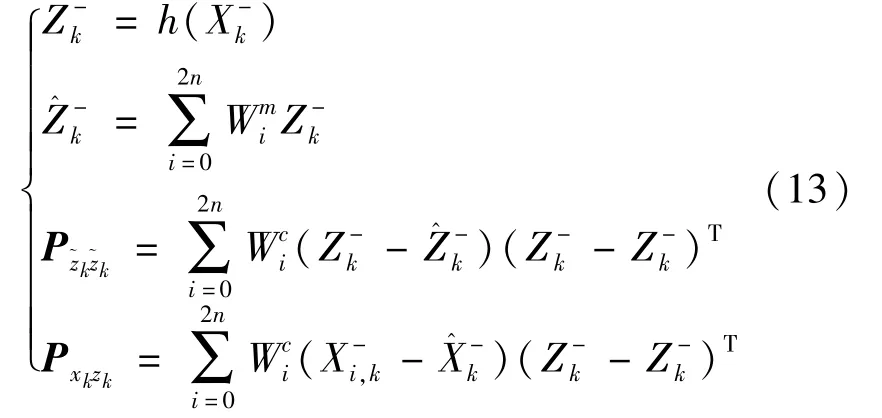
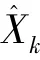
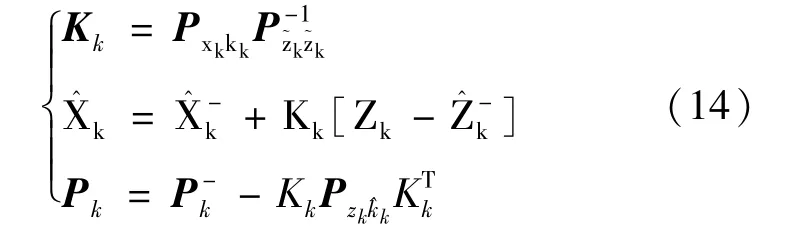
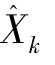
大气数据中的真空速V、攻角α、侧滑角β 均可由滤波的输出值经公式(6)计算得到。 马赫数是真空速与当地声速的比值,即


3 仿真实验
本文设计FADS/INS 的UKF 算法目的在于提高飞行器大气数据的估计精度,开展仿真实验验证算法性能,将滤波前测量结果的误差、EKF 算法误差和本文提出的UKF 滤波的误差进行对比。 模型由数据生成、单传感器信息预处理、EKF/UKF 传感器融合、飞行参数解算等部分组成。 整体框图如图1 所示,在对比仿真中,除滤波算法,模型的参数设置均相同。
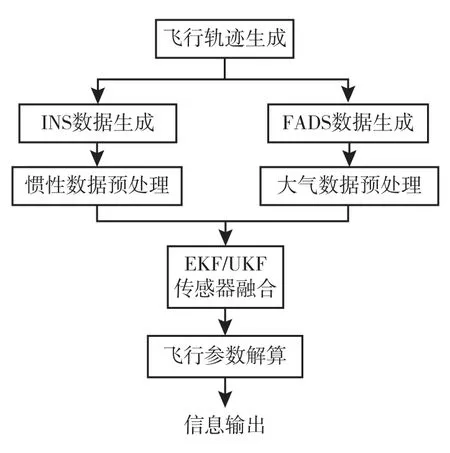
图1 仿真模型整体框图Fig.1 Overall block diagram of simulation model
飞行仿真条件如下:飞行高度起始值为3 km,上升段上升至20 km,巡航300 s 后下降至3 km;飞行马赫数上升段段从0.1 提升至7,下降段再由7下降为0.1;初始位置记为地面坐标系的(0,0,0)点,地面坐标系的X 轴朝向正东,Y 轴指向正北,由右手坐标系确定Z 轴垂直向下。 初始航向角0°,初始时刻飞行器坐标系与地面坐标系朝向相同,飞行器坐标系0 点位于地面坐标系的(0,0, -1000 m)处。 飞行总时长600 s,采样间隔1 Hz。
对惯性元件的误差建模,使用一阶高斯——马尔科夫过程,并且设定相关时间系数和标准差两个参数。 相关时间系数越小,一阶高斯—马尔科夫过程越趋近于白噪声表现(变化迅速)。 反之,系数越大,越趋近于随机游走表现(变化缓慢)。 标准差在一定程度上由测量设备的精度决定,仿真测试时设置加速度计的相关时间系数为0. 9,标准差为0.02 m/s,陀螺仪对角加速度的测量误差包括刻度因数误差、零偏、随机噪声与耦合误差,刻度因数误差和零偏误差可在装置内部进行一定精度的补偿,耦合误差因为数值很小通常忽略不计。 各孔压力数值由马赫数、攻角、侧滑角等参数的实际值求解并添加噪声而得,噪声服从一阶高斯——马尔科夫过程,相关时间系数0.5,标准差约为20 Pa。
3.1 真空速各轴分量估计结果
运行程序,EKF 与UKF 直接估计飞行器的三轴速度分量结果如图2 所示。

图2 滤波前后三轴速度分量对比Fig.2 Comparison of three⁃axis velocity components before and after filtering
两种滤波方法对速度均有很好的量测性和收敛性,随着迭代次数的增加,UKF 的实时性一直可以得到保证,但是EKF 的输出结果抖动较大,是在线性化过程中泰勒展开导致强非线性部分数据丢失的体现。
对比滤波前(仅INS)、EKF 和UKF 输出速度的大小,在600 s 的采样时间内,滤波前各轴速度平均误差之和为10.18 m/s,EKF 各轴速度平均误差之和为0. 98 m/s,UKF 各轴速度平均误差之和为0.38 m/s,不同方法滤波后各轴速度分量的误差随时间变化曲线如图3 所示。

图3 滤波后速度误差分量对比Fig.3 Comparison of velocity error components after filtering
因为飞行速度基数大,所以分析X 轴的速度——时间曲线,发现EKF 和UKF 的估计误差均较大,但两者相比,UKF 的误差比EKF 的小。 在Y和Z 轴分量上,UKF 的滤波效果明显好于EKF。
3.2 攻角、侧滑角估计误差
滤波后输出的各轴速度值由公式(6)计算可得攻角α 和侧滑角β 的估计值。 图4 和图5 给出了采用EKF 与UKF 得到的攻角和侧滑角随时间变化曲线,在整个仿真阶段,由UKF 估计的攻角和侧滑角误差小,且振荡幅度低。
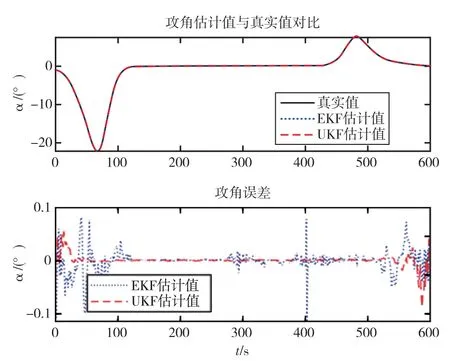
图4 不同方案估计攻角的值与误差Fig.4 Estimated angle of attack values and errors of different schemes
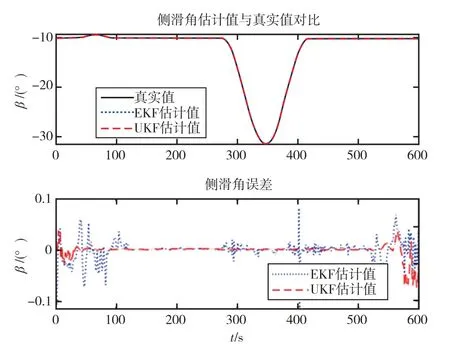
图5 不同方案估计侧滑角的值与误差Fig.5 Values and errors of side slip angle estimated by different schemes
α 和β 误差统计特性见表1。

表1 不同方案估计α、β 的误差结果对比(单次)Tab.1 Comparison of error of different schemes for estimating α and β(single time)
设定每次飞行时间500 s,运行100 次飞行仿真程序,不同方案估计α、β 的误差结果对比见表2。
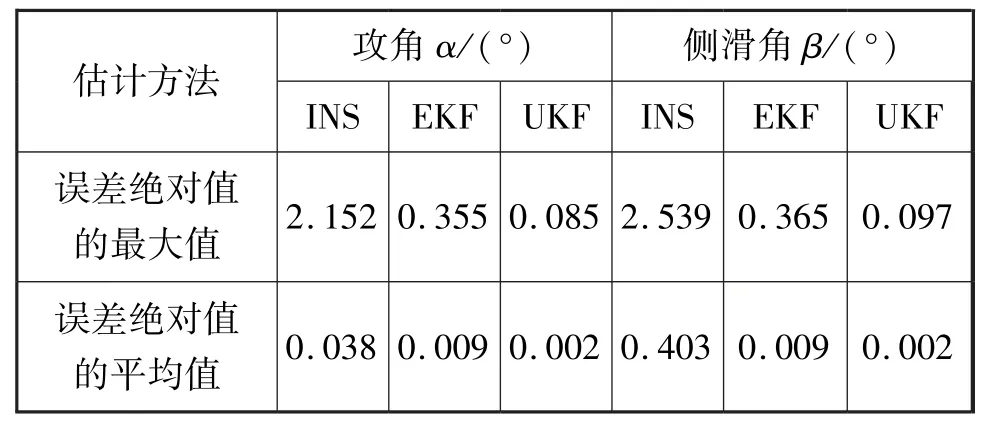
表2 不同方案估计α、β 的误差结果对比(100 次)Tab.2 Comparison of error of different schemes for estimating α and β(100 times)
从表1 和表2 数据可以得到结论:INS 直接估计的各项指标都是最差的,从数值上判断其估计效果最差,UKF 估计的效果最好,EKF 介于两者之间。
4 结束语
本文针对超音速飞行器在飞行时估计飞行数据时遇到的精度差、可靠性低等问题,提出了一种基于多传感器融合的大气数据估计算法。 经数据预处理、信息融合、飞行数据计算等步骤,输出马赫数、攻角和侧滑角。 仿真结果表明,采用UKF 的FADS/INS 融合估计方法与单传感器估计和EKF 估计方法相比,具有较高的精度和良好的稳定性,可为精确估计飞行器的大气参数提供支持,避免因参数估计错误而引起的事故。
但是本UKF 估计方法也具有一定的缺陷:没有分析非球形或楔形飞行器机头FADS 的模型结算方法,针对特殊形状的机头应单独进行空气动力学建模;其次,系统对风速建模时选择的是定常风,若大气紊流和突风较大,可能会影响算法的精确度,若能对模型进行改进,将更加有效地适用于各种飞行状态下的大气数据估计。

