最大似然估计法的教学设计与实践
赵小艳, 李继成, 段启宏
(西安交通大学数学与统计学院,西安 710049)
1 引 言
生活、工程、科学技术中碰到的很多量都是随机的,概率论与数理统计是高校各专业学生必修的一门基础课程.当前中学数学教材中包含了概率及运算、正态分布、统计图表、一元线性回归等一些概率统计课程内容,学生会计算相关的概率.然而,中学的应试教育使得学生对概率统计课程的思想方法掌握的不够,对运用概率知识解决实际问题了解的不够深入.
在互联网飞速发展的今天,大量数据的涌现使得概率统计的思想与方法成为各行业人员不可缺少的知识素养.因此,大学的概率统计课程应根据授课学生的情况重新设计教学内容,加强学生掌握概率统计的思想与方法,强化课程的应用.
概率统计的知识点比较多,学生不容易记忆并掌握.教师在讲各种方法时,一方面可以挖掘这些方法的产生过程、前后因果关系等,比如原来的方法在一类实际应用中不能满足需求,因此出现了另一种统计方法等;另一方面加强课程应用,将课本内容与当前的工程技术、科学技术相结合,设计应用案例,给教学不断注入新的血液,激发学生的学习热情.
概率统计中的最大似然估计法是参数估计的一种重要方法[1-4],参考文献[1-2]分别给出了最大似然估计的教学设计,通过引例给出最大似然估计法,说明该方法在实际生活中的应用等.然而以上这些教学设计中缺少该方法的产生过程、在科学技术中的具体应用等.
本文挖掘最大似然估计的产生过程、在机器学习中的应用等,重新设计最大似然估计的教学内容,目的是加强学生理解并掌握最大似然估计法的思想与方法,同时拓展学生知识视野,培养学生创新思维能力,深刻体会概率统计课程“源于生活,用于生活”的特点,学会用概率统计思想与方法指导学习与生活.
2 最大似然估计法的教学设计
本教学设计通过介绍现实生活中的例子,最大似然估计思想的产生过程,最大似然估计在机器学习中的应用,以及一代代数学家对最大似然估计概念内涵的不断深入挖掘的完整过程等,帮助学生体会最大似然估计理论的不断深化、应用场景的不断增多等事实,加强学生对最大似然估计思想与方法的理解与应用.
2.1 引例
频率学派认为,如果一次试验中随机事件A发生,则A发生的概率取大值比取小值合理.对一次随机抽到的样本值,要由此样本值估计未知参数,那么参数的取值应使得该样本出现的概率最大,这就是最大似然估计法的思想.
上面的描述学生不易理解,教师可以举一些生活中的例子,生动形象地来解释这一思想.
例1[3]一个老猎手和徒弟去打猎,看到一只兔子,每人打一枪,结果兔子被打中.后来发现兔子中了一枪,试问这一枪是谁打中的比较合理?
该例是经典案例,生活中经常使用这种方法思考并解决问题.在数学上,该方法有一个专业名称:最大似然估计法或极大似然估计法.
由于不同的参数对应不同的总体,最大似然估计法也可以看成是推断所得样本来自哪个总体或者总体分布.下面构造例2来说明这点.

2.2 最大似然估计
若离散型总体X的分布律为P{X=x}=p(x;θ1,θ2,…,θl),或连续型总体X的概率密度为f(x;θ1,θ2,…,θl)(对其他总体X,记其分布函数为F(x;θ1,θ2,…,θl)),其中θ1,θ2,…,θl是未知参数.
要估计总体中的未知参数θ1,θ2,…,θl,需要从总体X中抽取简单随机样本(X1,X2,…,Xn),且θ1,θ2,…,θl的取值应使得样本(X1,X2,…,Xn)出现的概率最大,为此,需计算样本(X1,X2,…,Xn)出现的概率.
对离散型总体X, (X1,X2,…,Xn)出现的概率是其分布律
(1)
对连续型总体X,要样本(X1,X2,…,Xn)出现的概率最大即要(X1,X2,…,Xn)的概率密度最大.(X1,X2,…,Xn)的概率密度为
(2)
固定(x1,x2,…,xn),将L(x1,x2,…,xn;θ1,θ2,…,θl)看成是参数θ1,θ2,…,θl的函数,称为θ1,θ2,…,θl的似然函数,简记为L(θ1,θ2,…,θl).

(3)
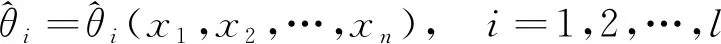
为求解(3),可以利用微积分的知识,对似然函数L(θ1,θ2,…,θl)求导并令其等于零,求得未知参数的表达式,并判断其是否是似然函数的最大值点,进而求得参数的最大似然估计.
然而,似然函数是样本的分布律或概率密度,是用连乘形式表示的,为了求解方便,数学上通常对似然函数L(θ1,θ2,…,θl)取对数得到lnL(θ1,θ2,…,θl),将乘积形式转化成求和形式,称lnL(θ1,θ2,…,θl)为对数似然函数.由于对数似然函数和似然函数具有相同的最大值点,因此对对数似然函数求导并令其等于零,解得参数θi的最大似然估计.
需要注意的是,求导数的方法并不总是奏效的,这时需要回到问题(3),运用其他方法求参数的估计值使得似然函数L(θ1,θ2,…,θl)取值最大.
2.3 最大似然估计法的产生过程
18世纪之前,天文学是运用数学最多的领域之一,天文学家依据天文数据建立模型,进行数据拟合等,解决了很多天文学问题.到18世纪,如何处理数据中的观测误差成为一个很棘手的问题.人们在数据处理中经常对数据取平均,经验表明算术平均值能够消除误差,提高精度.这样就产生下列问题:
(i) 测量中的误差应该服从什么概率分布?
(ii) 算术平均的优良性和误差分布有怎样的密切联系?
很多天文学家和数学家开始寻找误差分布曲线,伽利略、辛普森、拉普拉斯等先后讨论了随机误差的分布问题,得到了一些结论,然而这些结论都不能完美回答以上问题.
为了计算1801年1月天文学界出现的一颗从未见过的星(现在被称为谷神星)的轨迹,德国数学家高斯也研究了误差分布问题.高斯在1809年的著作《绕日天体运动的理论》的末尾一节“数据结合”中,用开创性的方法给出误差服从正态分布这一重要结论[5-6].那么高斯是如何推导出误差分布的呢?
为了确定参数θ的真值,对θ进行n次独立重复观测,测量值记为(x1,x2,…,xn),测量的误差记为ei=xi-θ,i=1,2,…,n.假设误差ei,i=1,2,…,n的概率密度为f(x),则测量θ得到观测值x的概率与f(x-θ)成比例,因此观测值(x1,x2,…,xn)出现的概率与f(x1-θ)f(x2-θ)…f(xn-θ)成比例.故可以取(x1,x2,…,xn)的概率分布为
L(θ)=f(x1-θ)f(x2-θ)…f(xn-θ) .
(4)
为了得到误差的概率密度,高斯提出以下两个开创性的方法:



高斯第一个开创性的方法就是最大似然估计的思想,第二个方法是把问题反过来思考:既然算术平均是一个好的估计,那么由第一个方法解出的参数估计值就应该是算术平均值.这两个创造性的想法充分展现了高斯的数学天才,最终高斯通过严谨的理论推导得出误差服从正态分布,又通过此分布的概率密度对处理数据的最小二乘法给了一个漂亮的解释[5-6].
虽然最小二乘法随后成为科学界处理数据的重要方法之一,可惜高斯提出的第一个方法在当时并没有引起数学界的重视.一直到1912年,英国统计学家Fisher在文章《关于拟合曲线的一个绝对准则》中再次提出了该方法,并命名为最大似然法.1922年Fisher又发表文章《理论统计学的数学基础》,证明了最大似然估计的一些性质.现在一般将最大似然估计法的发现归功于Fisher.
2.4 最大似然估计法在机器学习中的应用
在用机器学习[7]解决具体问题时,所包含的数据往往是无限的,不可能获取所有数据,因此也无法确切知道具体的数据分布.通常的做法是抽取训练数据集x=(x1,x2,…,xn),用训练数据的分析结果推测真实数据的性质.
为了对新的数据进行分析预测,需要基于训练数据集和对问题的元知识建立模型pmodel(x;θ).所建模型pmodel(x;θ)中含有未知参数θ,因此需要对θ进行估计.由于最大似然估计法能充分利用总体分布类型的信息,因此机器学习中经常计算θ的最大似然估计
(5)
或
(6)
关于机器学习中建立模型的方法论和高效求解最大似然估计的各种当代算法,请见参考文献[8]的详细介绍.
在最大似然估计教学中教师可以根据自己的思路,补充以上内容,加深学生对最大似然估计的思想与方法的理解与掌握.最大似然估计法在其他工程领域中也有很多应用,教师可以鼓励学生去发现和发掘.
3 教学实践与总结
作者于2020-2021学年在本校的电子、电气等专业教学大班进行此教学设计的实践,学生反映很好.从平常作业与期末考试试卷可以看出,90%的同学对最大似然估计法掌握的比较好.部分学生在教务处评教系统中留言:“课外补充形象”“特别善于举例”“举例仔细恰当”“开阔思路”等.也有学生留言,希望老师多讲一些概率统计方法的发展过程与实际应用.
在本节课后,部分同学和教师私下交流心得体会,感叹数学王子高斯的天才想法,创新的不易,甚至讨论如果没有高斯,是否也有其他学者提出该方法等.教师趁机鼓励学生,在学习和工作中要敢于质疑,有意识地培养学生的创新思维能力和大胆猜测小心求证的探索精神.
在讲解最大似然估计法、贝叶斯公式等在机器学习、通信技术等中的应用时,教室当时唏嘘一片,学生感觉有点不可思议.这个应用实例让学生深刻感受数学的重要性,教师趁机解释“数学无处不在,概率统计无处不在”,一些“高大上”的技术背后都是数学,要想解决“卡脖子”技术,提高我国科学技术水平,必须学好数学,用好数学,鼓励学生树立远大目标.
概率统计课程教学内容在科学技术和生活中都有很多应用,概率统计的思想与方法可以有效帮助我们做出合理的决策.教学中教师应将知识传授、课程应用与价值引领深度融合,充分挖掘课程的内涵,创新教学内容,加强课程应用,提高课程质量.
致谢非常感谢审稿人提出的建设性意见,感谢相关文献对本文的启发.

