具有小Gelfand-Kirillov维数Poisson Operad的商
王之梁,魏思凡,赵志兵
(安徽大学 数学科学学院, 安徽 合肥 230601)
Operad理论源于20世纪70年代Boardman-Vogt和May关于同伦论的研究, 与拓扑学、代数学、组合数学和数学物理等诸多领域都有着紧密联系[1-3]. 近年来, Operad理论在代数的结构理论、上同调理论与形变理论中的应用得到了代数学家们广泛的关注[4-7]. 粗略来说, Operad理论主要研究的是“运算”, 每一个Operad对应着一类代数系统. 例如, 控制结合代数的Ass、控制交换结合代数的Com、控制Lie代数的Lie、控制Poisson代数的Pois.从代数学角度来说, Operad本身也构成一个代数系统, 而它作为代数系统的结构性质与其控制的代数类的性质有着密切关系[2].
为了研究Operad的增长性质, 文献[6]中引入了Operad的Gelfand-Kirillov维数(简称GK维数)的概念. 论文通过Poisson Operad的截面理想来研究Poisson Operad的商的GK维数, 从而对GK维数分别为1,2,3,4的Poisson Operad的商进行了分类, 并给出了相应理想的具体形式.
1 预备知识
设n>0,k1,k2,…,kn≥0为正整数, 记
m1=0,mj=k1+k2+…+kj-1,m=k1+k2+…+kn,Bi=(mi+1,mi+2,…,mi+ki),
其中:2≤j≤n, 1≤i≤n.对任意的σ∈n,σi∈ki, 有下面的自然映射[3]
ϑn;k1,…,kn:n×k1×…×kn→m,
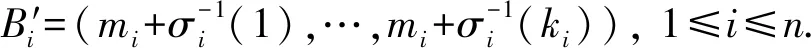
定义1[8]设P=(P(n))n≥0是右-模,1∈(1).若对任意的整数n>0,k1,k2,…,kn≥0, 有如下复合映射
∘:P(n)×P(k1)×…×P(kn)→P(k1+…+kn),

且满足下面3条公理:
(OP1) 对任意的θ∈P(n), 有
θ∘(1,…,1)=θ=1∘θ.
(OP2) 对任意的θ∈P(n),θi∈P(ki),θij∈P(lij),n>0,ki≥0,lij≥0,j∈{1,2,…,kj},i∈{1,2,…,n}, 有
θ∘(θ1∘(θ11,θ12,…,θ1k1),…,θn∘(θn1,θn2,…,θnkn))=
(θ∘(θ1,θ2,…,θn)∘(θ11,θ12,…,θ1k1,…,θn1,θn2,…,θnkn),
其中:若ki=0,则θi∘()=θi.
(OP3) 对任意的θ∈P(n),θi∈P(ki),σ∈n,σi∈ki,n>0,ki≥0,i∈{1,2,…,n}, 有
(θ*σ)∘(θ1*σ1,…,θn*σn)=(θ∘(θσ-1(n),…,θσ-1(n)))*ϑn;k1,…,kn(σ,σ1,…,σn),
则称P为对称Operad, 简称Operad, 其中1称为单位.
Operad有着多种形式的等价定义. 通常称定义1为Operad的经典定义 (classical definition), 有时使用下面Operad的偏定义(partial definition)会更加方便.
定义1′[8]设P=(P(n))n≥0是右-模,1∈P(1).若对任意的整数m>0,n≥0,1≤i≤m, 有如下偏复合映射
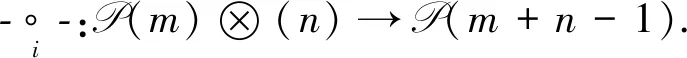
且满足以下3条公理:
(OP1′) 对任意的θ∈(n), 1≤i≤n, 有
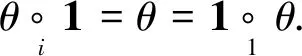
(OP2′) 对任意的λ∈P(l),μ∈P(m),v∈P(n), 有
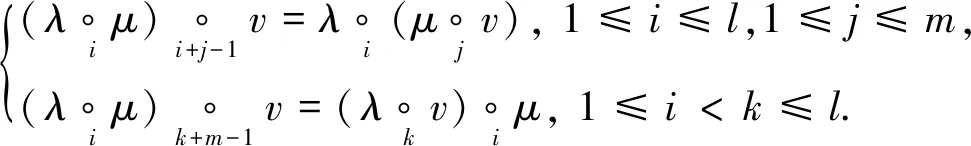
(OP3′) 对任意的μ∈P(m),v∈P(n),σ∈n,φ∈m, 有
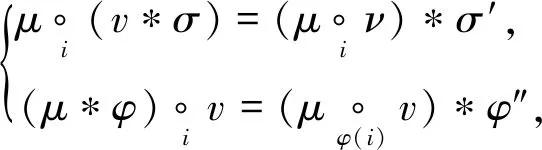
其中
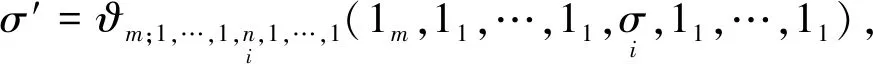
则称P为Operad.
Operad的经典定义与偏定义是等价的,参见文献[8]. 事实上, 复合映射与偏复合映射有如下转换关系[1]
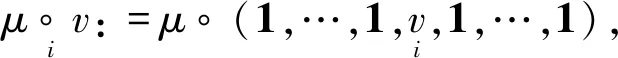
设I=(I(n))n≥0是Operad P=(P(n))n≥0的右-子模. 若对任意m>0,n≥0,1≤i≤m, 有
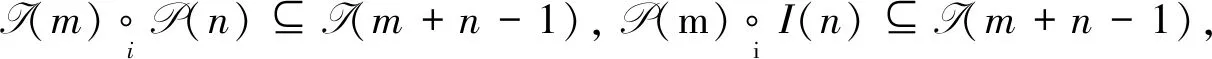
则称I为P的理想[1].显然, 对于理想I, 右-模P/I作成一个Operad, 称P/I为 关于理想I的商Operad, 简称商Operad.
定义2[6]设P是Operad, 单位记为1, 有时记为11,有:
(2) 设P是酉Operad. 若存在12∈P(2), 满足对任意的θ∈P(n),有
12∘(θ,10)=θ=12∘(10,θ),
则称P为2-酉Operad, 称12为2-单位.
(3) 如果P(1)=11, 则称P为连通的.
(4) 若P为2-酉Operad, 对任意正整数n≥3, 归纳定义
1n=12∘(1n-1,11),1′n=12∘(11,1n-1),
若1n=1′n, 则称1n为n-单位.
记集合[n]:={1,2,…,n}.设P是酉Operad. 对于I⊆[n], 称映射

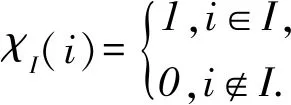
若I={i1,i2,…,is},1≤i1 定义3[6]设P是酉Operad,k是正整数,kr=(kr(n))n≥0为P的-子模, 其中 约定0rP=P. 容易验证krP是P的理想, 称krP为P的第k个截面理想. 定义4[6]设P=(P(n))n≥0是Operad,有: (1) 若每个P(n)都是有限维的, 则称P为局部有限的. (2) 若P是局部有限的, dimP(n)=dn,n≥0,则称(d0,d1,…,dn,…)为P的维数序列. 记 称GKdimP为P的GK维数. 设P是局部有限的, I是P的理想,kr是P的第k个截面理想, 记 b={b0,b1,b2,…} 为a的二项式变换. 命题1[3]设数列{fI(n)}是数列{dimI(n)}的二项式变换, 则 GKdimI=max{k|fI(k)≠0}+1, Poisson Operad是指控制Poisson代数的Operad, 记为Pois.设E=12⊕τ为右2-模, 其中模作用为 12*(12)=12,τ*(12)=-τ. 则Pois可由{10,12,τ}按如下关系生成 显然, Pois(0)=10, Pois(1)=11, Pois(2)=E, Pois(3)有-基{13,θ1,…,θ5}, 其中 不难验证Poisson Operad具有以下性质: (1) Pois是连通的2-酉Operad, 且1n=1′n. (2) 对每个n≥0,Pois(n)是右n-正则模, 即Pois(n)≅n. 下面考虑Poison Operad上截面理想的一些性质 引理1设kr是Pois的第k个截面理想. 则1r=2r=〈τ〉, 其中〈τ〉为由τ生成的理想. 所以有k-向量空间分解 Pois(n)=1n⊕〈τ〉(n). 任取θ∈2r(n),n≥3, 设θ=a1n+θ′, 其中a∈,θ′∈〈τ〉(n).由2r的定义知, 对任意的1≤i≤n,有 故a=0, 从而θ=θ′∈〈τ〉(n).因此2r=〈τ〉. 引理2设I是Pois的真理想,kr为Pois的第k个截面理想,则I⊆3r或者I=2r. 证明首先, 断言若I是Pois的真理想,则I⊆2r.事实上, 若I⊄2r, 则存在θ∈I(n),n≥1,i∈[n], 使得πi(θ)=a11≠0,a∈.此时,11∈I(1), 故I=Pois, 这与I是真理想矛盾, 故I⊆2r. 其次, 若I⊄3r, 则存在θ∈I(n),n≥2, 1≤i πi,j(θ)∈I(2)⊆2r(2), 以及引理1可知,πi,j(θ)=bτ≠0,b∈.从而τ∈I(2).因此I=2r. 引理3设kr为Pois的第k个截面理想,θ∈Pois(n),n是整数且n≥k≥0,则: (1)τ∘(θ,11)∈k+1r(n+1)当且仅当θ∈kr(n). (2)12∘(θ,τ)∈k+2r(n+2)当且仅当θ∈kr(n). 证明(1) 设θ∈Pois(n)满足τ∘(θ,11)∈k+1r(n+1), 则对任意的J⊆[n+1],|J|=k,有πJ(τ∘(θ,11))=0.任取I⊆[n],|I|=k-1, 令J=I∪{n+1}, 则 τ∘(πI(θ),11)=(τ∘(θ,11))∘(1χJ(1),…,1χJ(n),1χJ(n+1))=0, 故πI(θ)=0.由I的任意性可知,θ∈kr(n). 反之, 设θ∈kr(n).任取I⊆[n+1],|I|=k.当n+1∉I时,有 πI(τ∘(θ,11))=τ∘(θ∘(1χI(1),1χI(2),…,1χI(n)),10)=0. 当n+1∈I时, 记I′=I∩[n],|I′|=k-1.因为θ∈kr(n), 所以 πI(τ∘(θ,11))=τ∘(πI′(θ),11)=0, 因此τ∘(θ,11)∈k+1r(n+1). (2) 设θ∈Pois(n)满足12∘(θ,τ)∈k+2r(n+2),则对任意的J⊆[n+2],|J|=k+1,有 πJ(12∘(θ,τ))=0. 任取I⊆[n],|I|=k-1, 令 J=I∪{n+1}∪{n+2}, 则 12∘(πI(θ),τ∘(11,11))=0, 故πI(θ)=0.由I的任意性可知,θ∈kr(n). 反之, 设θ∈kr(n).任取J⊆[n+2],|J|=k+1, 记I=J∩[n].当n+1∈J,n+2∈J时, 因为θ∈kr(n), 所以 πI(12∘(θ,τ))=12∘(πI(θ),τ)=0. 当n+1∉J,n+2∈J或n+1∈J,n+2∉J时,有 πI(12∘(θ,τ))=12∘(πI(θ),0)=0. 引理4设kr为Pois的第k个截面理想,I是Pois的非零理想,k是正整数,则: (1) 对任一k≫0, 有I∩kr≠I∩k+1r; (2) 对任一k≥2, 有kr≠k+1r. τ∘(θ,11)∈k0+1r(n+1),τ∘(θ,11)∉k0+2r(n+1), 即I∩k0+1r≠I∩k0+2r.由归纳法可知对所有的k≥k0有I∩kr≠I∩k+1r. (2) 根据(1)和τ∈2r,τ∉3r可知,当k≥2时, 有kr≠k+1r. Gelfand-Kirillov维数(或称为GK维数)是研究-分次代数和Operad的重要工具, 它可以来描述Operad的增长性质. 若Operad P的GK维数有限, 则有限生成的P-代数的GK维数都是有限的, 且Operad P的GK维数和P-代数A的GK维数之间有如下关系 GKdimA≤GKdimP+r-1, 其中:r为P-代数A的生成元的个数[6]. 关于2-酉Operad及其商的GK维数, 文献[6]给出了下面两个重要结果. 命题2[6]设P是2-酉Operad, I是P的理想, 则rP/I≅rP/(rP∩I). 命题3[6]设P是2-酉Operad, 则GKdimP<∞当且仅当存在正整数k, 使得krP=0,且 GKdimP=max{k|kr≠0}+1=min{k|kr=0}. 下面给出文章的主要结果. 定理1设I是Pois的理想, 记P=Pois/I,kr和rP分别是Pois和P的第k个截面理想,k是正整数,则GKdimP≤k当且仅当kr⊆I.特别地,有 证明由命题3可知GKdim≤k当且仅当krP=0.因此由命题2可得GKdim≤k当且仅当kr⊆I.结合命题1,2,可得 GKdim(Pois/kr)=max{n|fPois/kr(n)=dimnrPois/kr(n)=dim(nr/(nr∩kr))(n)≠0}+1. (1) 由于截面理想是降链[1], 由引理1,4可知 1r=2r3r…nr…, (2) 因此,当k=1时,有 故GKdim(Pois/1r)=1.因为1r=2r, 所以GKdim(Pois/2r)=1.若k≥3, 由命题1知 因此,对所有的l≠1,有fPois(l)≠0, 故dimk-1r(k-1)≠0.由(2)知, 当n≥k时,有 fPois/kr(n)=dim(nr/(nr∩kr))(n)=dim(nr/nr)(n)=0, 当n=k-1时,有 fPois/kr(k-1)=dim(k-1r/(k-1r∩kr))(k-1)=dimk-1r(k-1)≠0, 因而,GKdim(Pois/kr)=k-1+1=k. 下述定理给出了Poisson Operad的商Operad在GK维数小于等于4时的分类. 定理2设I是Pois的一个理想. 记P=Pois/I, GKdimP=n,kr和krP分别是Pois和P的第k个截面理想, 则: (1) 当n=1时, P=Pois/1r; (2)n的值不为2; (3) 当n=3时, P=Pois/3r; (4) 当n=4时, P=Pois/4r. 证明(1) 因为GKdimP=1, 所以由定理1可知1r⊆I且PoisI.根据引理2得 I=2r=1r. (2) 因为 fP(1)=dim1rP(1)=dim2rP(1)=0且P=Pois/I, 所以,由命题1可知GKdimP=1或者GKdimP≥3. (3) 因为GKdimP=3, 所以由定理1可知3r⊆I且PoisI.根据引理2得I=2r或者 I⊆3r.若I=2r, 则GKdimP=GKdim(Pois/2r)=1, 这与GKdimP=3矛盾, 故I⊆3r.于是I=3r. (4) 因为P是酉Operad, 所以 fP(0)=dim0rP(0)=dimP(0)=dimP(1)=1. 由GKdimP=4可知fP(3)≠0,fP(k)=0, 其中k≥4, 且I≠2r, PoisI.根据引理2知I⊆3r, 因此I(2)=0, 于是 dimP(2)=dim(Pois/I)(2)=dimPois(2)-dimI(2)=2. 因为{fP(n)}是{dimP(n)}的二项式变换, 所以 因此fP(1)=0,fP(2)=1.易知3r(3)=k1θ4+k2θ5, 其中k1,k2∈,因此3r(3)是个单模. 因为I(3)是3r(3)的子模, 所以I(3)=3r(3)或者I(3)=0.若I(3)=3r(3), 则 dim(3)=dimPois(3)-dimI(3)=4. 因为 所以fP(3)=0, 这与fP(3)≠0矛盾, 因此I(3)=0,fP(3)=2.同理可知 从而有dimI(n)=dim4r(n).由定理1可知4r⊆I, 因此I=4r. 对GK维数为5的Poisson Operad的商Operad,有如下的断言. 定理3设I是Pois的理想.记PI=Pois/I,kr和krPI分别是Pois和PI的第k个截面理想, 则至少存在两个非同构的PI,使得GKdim=5. 证明根据引理1可知, 当k≥4时, Lie(k)是右k-模kr(k)的真子模, 因此4r(4)有非零4-真子模M.因为Pois(1)=11, 所以对任意的v∈Pois(1),m∈M,有其中1≤i≤k.由文献[6]命题3.2可知 krM(n)={μ∈kr(n)|πI(μ)∈M,∀I⊆[n],|I|=k} 是Pois的理想. 可以通过M的选择使得4r4rM5r, 因此 GKdim(Pois/5r)=5=GKdim(Pois/4rM) 因为4rM和5r的维数序列不同, 所以Pois/5r和Pois/4rM不同构.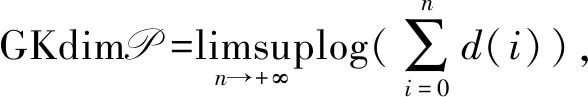
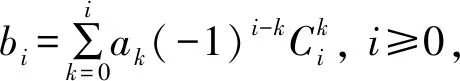
2 Poisson Operad的截面理想
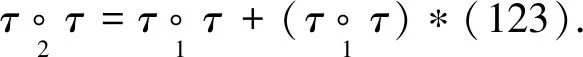
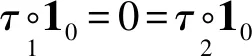
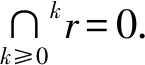
3 Poisson Operad的商

