双重逆极限空间中极限跟踪性与弱Specification性的研究
冀占江,张更容
(1.梧州学院 大数据与软件工程学院,广西高校图像处理与智能信息系统重点实验室,广西 梧州 543002;2.湖南第一师范学院 数学与计算科学学院,湖南 长沙 410205)
在动力系统(X,f)的研究中,由于连续映射f不一定是同胚的,因此系统(X,f)是不可逆的.为了克服这种不可逆性,学者在逆极限空间中引入与f相关的移位映射σf,由于移位映射σf是同胚的,这就为研究移位映射σf的动力学性质带来了很大方便,很多学者通过研究逆极限空间上移位映射σf的动力学性质来揭示原空间X上自映射f的动力学性质,至今为止逆极限空间的理论已经非常成熟[1-5].随着动力系统的发展和问题研究的深入,人们发现逆极限空间中有限个符号已经难以解决生活中的实际问题.文献[6-7]将逆极限空间的概念推广到双重逆极限空间,双重逆极限空间上的理论尚不完善,有待进一步研究.跟踪性和弱Specification是在动力系统中非常重要的概念,不仅与系统的稳定性密切相关,也与其他学科的发展联系紧密[8-15].论文受文献[8-9]研究思路的启发,给出双重逆极限空间上极限跟踪性和弱Specification性的概念,利用自映射f∘g与移位映射σf∘σg之间的关系,得到如下结果:映射f∘g具有极限跟踪性当且仅当移位映射σf∘σg具有极限跟踪性,映射f∘g具有弱Specification性当且仅当移位映射σf∘σg具有弱Specification性.从而推广和改进了文献[8-9]的结果,为极限跟踪性和弱Specification性在其他学科的应用提供了理论支撑.
1 基本概念
定义1设X,Y是拓扑空间,称f是一个同胚映射,如果f:X→Y是一个一一映射,并且f和f-1都是连续的.
定义2[6]设(X,d)是紧致度量空间,f:X→X,g:X→X连续映射,f∘g=g∘f,记集合


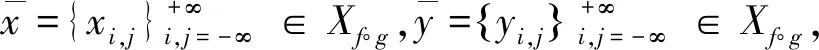
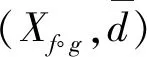
定义移位映射σf∘g:Xf∘g→Xf∘g为
则σf∘g是同胚映射,并且σf∘σg=σg∘σf,i,j∈.
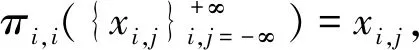
定义3设(X,d)是度量空间,f:X→X连续,称f具有极限跟踪性,如果对任意的极限伪轨{xi}i≥0,存在y∈X,y极限跟踪{xi}i≥0.


定义5设(X,d)是紧致度量空间,f:X→X,g:X→X为同胚映射,
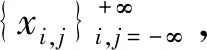
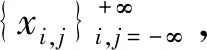
定义7[9]设(X,d)是紧致度量空间,f:X→X连续,称f具有弱Specification性,如果∀ε>0,∃M=M(ε)>0,任取X中序列{xi}i≥0,任取满足0≤ai≤bi 注2仿照f具有弱Specification性的定义,下面给出双重映射f∘g有弱Specification性的概念. 定理1设(X,d)是紧致度量空间,f:X→X,g:X→X都是同胚映射,且f∘g=g∘f,则f∘g具有极限跟踪性当且仅当σf∘σg具有极限跟踪性. 证明假设f∘g具有极限跟踪性.由于X是紧致度量空间,故X是有界的,令M=diam(X).对任意的ε>0,存在m1>0,n1>0满足 由f和g一致连续性知,对ε>0,存在0<δ1<ε,对任意的0≤i≤2m1和0≤j≤2n1,当d(u,v)<δ1时,有 d(figj(u),figj(v))<ε. (1) 则存在N1∈+,当s,t>N1时,有 故对δ1>0,存在N2∈+,当s,t>N2时,有 由(1)式知,当s,t>N2,0≤i≤2m1,0≤j≤2n1时,有 (2) figj(yh,k)=figj(fm1-hgn1-k(x))=fm1-(h-i)gn1-(k-j)(x)=yh-i,k-j, 当|h|>m1或|k|>n1时,有 当|h|≤m1,|k|≤n1时,令m1-h=i,n1-k=j,则0≤i≤2m1,0≤j≤2n1,有 故当s,t>N2时,由(2)式有 因此,当s,t>N2时,∀h,k∈,有 假设σf∘σg具有极限跟踪性. ∀η>0,存在m2>0,n2>0,满足 由f和g一致连续性知,对η>0,存在0<δ2<η,对任意的0≤s≤2m2和0≤t≤2n2,当d(u,v)<δ2时,有 d(fsgt(u),fsgt(v))<η. (3) d(fg(yi,j),yi+1,j+1)<δ2. 由(3)式知,当i,j>N3,0≤s≤2m2,0≤t≤2n2时,有 d(fs+1gt+1(yi,j),fsgt(yi+1,j+1))<η. (4) 易知 当|h|>m2或|k|>n2时,有 当|h|≤m2,|k|≤n2时,令m2-h=s,n2-k=t,则0≤s≤2m2,0≤t≤2n2,并且有 故当i,j>N3时,由(4)式有 则当i,j>N3时,∀h,k∈,有 定理2设(X,d)是紧致度量空间,f:X→X,g:X→X都是同胚映射,且f∘g=g∘f,则f∘g具有弱Specification性当且仅当σf∘σg具有弱Specification性. 证明设f∘g具有弱Specification性.由于X是紧致度量空间,故X是有界的,令T=diam(X).∀ε>0,∃m1>0,n1>0,满足 由f和g一致连续性知,对ε>0,存在0<δ<ε,对任意的0≤k≤2m1和0≤h≤2n1,当d(u,v)<δ时,有 d(fkgh(u),fkgh(v))<ε. (5) 由(5)式知,当0≤k≤2m1,0≤h≤2n1时,对任意的i,j∈,ai≤m≤bi,cj≤n≤dj,有 (6) figj(ys,t)=figj(fm1-sgn1-t(xm1,n1))=fm1-(s-i)gn1-(t-j)(xm1,n1)=ys-i,t-j, 当|s|>m1或|t|>n1时,有 当|s|≤m1,|t|≤n1时,令m1-s=k,n1-t=h,则0≤k≤2m1,0≤h≤2n1,再结合(6)式可得 故对任意的i,j∈,ai≤m≤bi,cj≤n≤dj,有 则σf∘σg具有弱Specification性.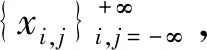
2 主要结果
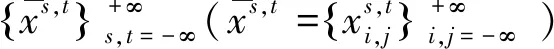
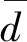




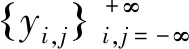


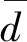
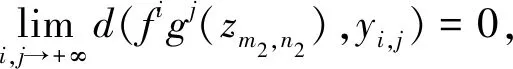
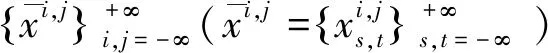


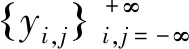
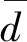
3 结束语


