(α,β)-γ-正则开集和(α,β)-γ-极不连通空间
吴耀强
(宿迁学院 文理学院,江苏 宿迁 223800)
自从文献[1-2]引入半开集和算子概念以来,许多拓扑学者先后定义了一些不同形式的近似开集.如文献[3-4]分别给出了两种推广型开集——α-开集、γ-开集,并进一步研究了它们相应的连通性、分离性;文献[5-6]分别提出双算子开集;文献[7]给出多算子开集并得到一些新的结果. 此外,文献[8]提出极不连通空间概念后,极不连通空间也成为拓扑学者研究的课题之一[9-15]. 论文继续基于(α,β)-γ-开集给出多算子正则开集概念,进一步研究(α,β)-γ-极不连通空间和(α,β)-γ-超连通空间,并利用(α,β)-γ-正则开集得到(α,β)-γ-极不连通空间的拓扑刻画.
论文中X是非空集合,(X,T)是拓扑空间(或简称X是拓扑空间),并用P(X),T,F分别表示X的幂集族、开集族与闭集族.设A⊂X,用cl(A),int(A)分别表示为A的闭包与内部.论文未申明的概念与记号均引自文献[1,7].
定义1[2]设X是拓扑空间,设α:T→P(X), 若对于任意V∈T,均有V⊂α(V),则称α为在集合X在T上的一个算子,或简称α为T的一个算子.
定义2[3,5,7]设X是拓扑空间,α,β,γ为T的算子,A,B,C⊂X,有
(1) 若∀x∈A,总存在U∈T,使得x∈U且α(U)⊂A,则称A是α-开集,并记Tα为α-开集族;
(2) 若∀x∈B,总存在U∈Tβ,使得x∈U且α(U)⊂B,则称B是(α,β)-开集,并记T(α,β)为(α,β)-开集族;
(3) 若∀x∈C,总存在U,V∈Tγ,使得x∈U,x∈V且α(U)∪β(V)⊂C,则称C是(α,β)-γ-开集,XC是(α,β)-γ-闭集.记T(α,β)-γ,F(α,β)-γ分别为(α,β)-γ-开集族和(α,β)-γ-闭集族,cl(α,β)-γ(C)=∩{F|F∈F(α,β)-γ,且C⊂F},int(α,β)-γ(C)=∪{U|U∈T(α,β)-γ,且U⊂C},并称cl(α,β)-γ(C),int(α,β)-γ(C)分别为C的(α,β)-γ-闭包与(α,β)-γ-内部.
由上述定义易知α-开集族、(α,β)-开集族、(α,β)-γ-开集族均保持集合的并运算.
定义3[2]设X是拓扑空间,α为T的算子,若x∈X,对于任意U,V∈T,其中x∈U,x∈V,总存在W∈T且x∈W,使得α(W)⊂α(U)∩α(V),则称α为T的正则算子.
定义4设X是拓扑空间,α,β,γ为T的算子,若x∈X,对于任意U,V∈Tγ,其中x∈U,x∈V,总存在W∈Tγ且x∈W,使得α(W)⊂α(U)∩α(V),则称(α,γ)为T的正则双算子.
命题设X是拓扑空间,α,β,γ为T的算子,(α,γ),(β,γ)均为T的正则双算子,对于∀C1,C2∈T(α,β)-γ,则C1∩C2∈T(α,β)-γ.
证明设C1,C2∈T(α,β)-γ,对于∀x∈C1∩C2,有x∈C1且x∈C2.由定义2(3)知,存在Ui,Vi∈Tγ,使得x∈Ui,x∈Vi且α(Ui)∪β(Vi)⊂Ci(这里i=1,2),有
(α(U1)∩α(U2))∪(β(V1)∩β(V2))⊂(α(U1)∪β(V1))∩(α(U2)∪β(V2))⊂C1∩C2.
(*)
既然(α,γ),(β,γ)均为T的正则双算子,根据定义4可知,存在W1∈Tγ且x∈W1,使得α(W1)⊂α(U1)∩α(U2),以及存在W2∈Tγ且x∈W2,使得β(W2)⊂β(V1)∩β(V2),根据(*)可得α(W1)∪β(W2)⊂C1∩C2,故C1∩C2∈T(α,β)-γ.
定理1[7]设X是拓扑空间,α,β,γ为T的算子,A,B⊂X,则下列结论成立:
(1)x∈cl(α,β)-γ(A)⟺∀C∈T(α,β)-γ且∀x∈C,有C∩A≠∅ ;
(2) int(α,β)-γ(A)⊂A⊂cl(α,β)-γ(A) ;
(3)A⊂B⟹cl(α,β)-γ(A)⊂cl(α,β)-γ(B),int(α,β)-γ(A)⊂int(α,β)-γ(B) ;
(4)A∈F(α,β)-γ⟺cl(α,β)-γ(A)=A;B∈T(α,β)-γ⟺int(α,β)-γ(B)=B;
(5) cl(α,β)-γ(cl(α,β)-γ(A))=cl(α,β)-γ(A), 即 cl(α,β)-γ(A)∈F(α,β)-γ;int(α,β)-γ(int(α,β)-γ(B))=int(α,β)-γ(B), 亦即 int(α,β)-γ(B)∈T(α,β)-γ;
(6) 设(α,γ),(β,γ)均为T的正则双算子,∀C∈T(α,β)-γ,有cl(α,β)-γ(A)∩C⊂cl(α,β)-γ(A∩C),∀D∈F(α,β)-γ,有int(α,β)-γ(B)∪D⊂cl(α,β)-γ(B∪D);
(7) 设(α,γ),(β,γ)均为T的正则双算子,有cl(α,β)-γ(A∪B)=cl(α,β)-γ(A)∪cl(α,β)-γ(B),int(α,β)-γ(A∩B)=int(α,β)-γ(A)∩int(α,β)-γ(B);
(8) cl(α,β)-γ(XA)=Xint(α,β)-γ(A),cl(α,β)-γ(A)=Xint(α,β)-γ(XA),int(α,β)-γ(XA)=Xcl(α,β)-γ(A),int(α,β)-γ(A)=Xcl(α,β)-γ(XA).
定义5设X是拓扑空间,α,β,γ为T的算子,D⊂X,若cl(α,β)-γ(D)=X,则称D为X的一个(α,β)-γ-稠密子集.
定义6设X是拓扑空间,α,β,γ为T的算子,U,V⊂X,有:
(1) 若U=int(α,β)-γ(cl(α,β)-γ(U)),则称U为X的一个(α,β)-γ-正则开集;
(2) 若V=cl(α,β)-γ(int(α,β)-γ(V)),则称V为X的一个(α,β)-γ-正则闭集.
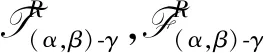
注1(α,β)-γ-正则开集与正则开集是两个独立的概念.

定理2设X是拓扑空间,α,β,γ为T的算子,U,V⊂X,有
(1)U⊂cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U)))⟺cl(α,β)-γ(U)=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U)));
(2)V⊃int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(V)))⟺int(α,β)-γ(V)=int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(V))).
证明仅证结论(1) ,结论(2)可类似给出证明.
“⟹”.设U⊂cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U))),知U⊂cl(α,β)-γ(U)⊂cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U)));另外,易知int(α,β)-γ(cl(α,β)-γ(U))⊂cl(α,β)-γ(U),由定理1可得cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U)))⊂cl(α,β)-γ(U),从而cl(α,β)-γ(U)=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U))).
“⟸”.由于U⊂cl(α,β)-γ(U),显然可得U⊂cl(α,β)-γ(U)=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U))).
推论设X是拓扑空间,α,β,γ为T的算子,U⊂X,有
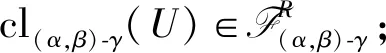
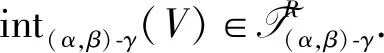
引理1设X是拓扑空间,α,β,γ为T的算子,U,V⊂X,有


证明仅证结论(1) ,结论(2)可类似给出证明.
一方面,由于int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U)))⊂cl(α,β)-γ(int(α,β)-γ(U)),显然可得
cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U))))⊂cl(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U)))=cl(α,β)-γ(int(α,β)-γ(U)).
由int(α,β)-γ(U)⊂cl(α,β)-γ(int(α,β)-γ(U))可得
int(α,β)-γ(int(α,β)-γ(U))⊂int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U))),
即int(α,β)-γ(U)⊂int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U))),故
cl(α,β)-γ(int(α,β)-γ(U))⊂cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U)))),
故
cl(α,β)-γ(int(α,β)-γ(U))=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U)))),
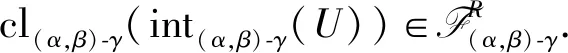
引理2设X是拓扑空间,α,β,γ为T的算子,(α,γ),(β,γ)均为T的正则双算子,U,V∈T(α,β)-γ,则有如下结论:
(1) int(α,β)-γ(cl(α,β)-γ(U))∩int(α,β)-γ(cl(α,β)-γ(V))=int(α,β)-γ(cl(α,β)-γ(U∩V));
(2) cl(α,β)-γ(int(α,β)-γ(U))∪cl(α,β)-γ(int(α,β)-γ(V))=cl(α,β)-γ(int(α,β)-γ(U∪V)).
证明仅证结论(1) ,结论(2)可类似给出证明.
利用定理1(6),(7)知
int(α,β)-γ(cl(α,β)-γ(U))∩int(α,β)-γ(cl(α,β)-γ(V))=int(α,β)-γ(cl(α,β)-γ(U)∩cl(α,β)-γ(V))⊂
int(α,β)-γ(cl(α,β)-γ(U∩cl(α,β)-γ(V)))⊂int(α,β)-γ(cl(α,β)-γ(cl(α,β)-γ(U∩V)))=int(α,β)-γ(cl(α,β)-γ(U∩V)).
另外,由于cl(α,β)-γ(U∩V)⊂cl(α,β)-γ(U)∩cl(α,β)-γ(V),可得
int(α,β)-γ(cl(α,β)-γ(U∩V))⊂int(α,β)-γ(cl(α,β)-γ(U)∩cl(α,β)-γ(V))=
int(α,β)-γ(cl(α,β)-γ(U))∩int(α,β)-γ(cl(α,β)-γ(V)),
从而得证.
引理3设X是拓扑空间,α,β,γ为T的算子,(α,γ),(β,γ)均为T的正则双算子,若X中任意两个无交的(α,β)-γ-开集的(α,β)-γ-闭包无交当且仅当X中任意两个无交的(α,β)-γ-正则开集的(α,β)-γ-闭包无交.
证明“⟹”显然.


1 (α,β)-γ-极不连通空间
定义7设X是拓扑空间,α,β,γ为T的算子,若 ∀U∈T(α,β)-γ,有cl(α,β)-γ(U)∈T(α,β)-γ,则称X为(α,β)-γ-极不连通空间.事实上,也可以给出(α, β)-γ-极不连通的等价定义:若 ∀V∈F(α,β)-γ,有int(α,β)-γ(V)∈F(α,β)-γ.
定理3设X是拓扑空间,α,β,γ为T的算子,(α,γ),(β,γ)均为T的正则双算子,则下列条件等价:
(1)X为(α,β)-γ-极不连通空间;
(2) ∀U,V∈T(α,β)-γ,若U∩V=∅,则cl(α,β)-γ(U)∩cl(α,β)-γ(V)=∅;
(3) ∀U∈T(α,β)-γ,D⊂X,若U∩D=∅,则cl(α,β)-γ(U)∩cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(D)))=∅.
证明(1)⟹(2).∀U,V∈T(α,β)-γ,且U∩V=∅,易得cl(α,β)-γ(U)∩int(α,β)-γ(V)=∅,进而cl(α,β)-γ(U)∩V=∅,从而int(α,β)-γ(cl(α,β)-γ(U))∩cl(α,β)-γ(V)=∅,故cl(α,β)-γ(U)∩cl(α,β)-γ(V)=∅.
(2)⟹(1).设U∈T(α,β)-γ,易知int(α,β)-γ(cl(α,β)-γ(U))⊂cl(α,β)-γ(U),且XU∈F(α,β)-γ,即int(α,β)-γ(XU)∈T(α,β)-γ,当然U∩int(α,β)-γ(XU)=∅.可得cl(α,β)-γ(U)∩cl(α,β)-γ(int(α,β)-γ(XU))=∅,根据定理1可知cl(α,β)-γ(U)∩cl(α,β)-γ(Xcl(α,β)-γ(U))=∅,即cl(α,β)-γ(U)∩(Xint(α,β)-γ(cl(α,β)-γ(U)))=∅,所以cl(α,β)-γ(U)⊂int(α,β)-γ(cl(α,β)-γ(U)).于是cl(α,β)-γ(U)=int(α,β)-γ(cl(α,β)-γ(U)),即cl(α,β)-γ(U)∈T(α,β)-γ,从而X为(α,β)-γ-极不连通空间.

定理4设X是拓扑空间,α,β,γ为T的算子,(α,γ),(β,γ)均为T的正则双算子,则下列条件等价:
(1)X为(α,β)-γ-极不连通空间;
(2) ∀U,V∈T(α,β)-γ,有cl(α,β)-γ(U)∩cl(α,β)-γ(V)=cl(α,β)-γ(U∩V);
(2*) ∀U*,V*∈F(α,β)-γ,有int(α,β)-γ(U*)∪int(α,β)-γ(V*)=int(α,β)-γ(U*∪V*);
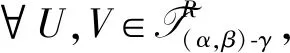
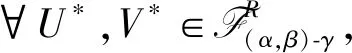
(4) ∀U,V∈T(α,β)-γ,有int(α,β)-γ(cl(α,β)-γ(U))∪int(α,β)-γ(cl(α,β)-γ(V))=int(α,β)-γ(cl(α,β)-γ(U∪V));
(4*) ∀U*,V*∈F(α,β)-γ,有cl(α,β)-γ(int(α,β)-γ(U*))∩cl(α,β)-γ(int(α,β)-γ(V*))=cl(α,β)-γ(int(α,β)-γ(U*∩V*)).
证明(1)⟹(2).由于X为(α,β)-γ-极不连通空间,则∀U,V∈T(α,β)-γ,有cl(α,β)-γ(U),cl(α,β)-γ(V)∈T(α,β)-γ,且cl(α,β)-γ(U∩V)∈T(α,β)-γ,进而int(α,β)-γ(cl(α,β)-γ(U))=cl(α,β)-γ(U),int(α,β)-γ(cl(α,β)-γ(V))=cl(α,β)-γ(V),则int(α,β)-γ(cl(α,β)-γ(U))∩int(α,β)-γ(cl(α,β)-γ(V))=cl(α,β)-γ(U)∩cl(α,β)-γ(V),又由引理2知int(α,β)-γ(cl(α,β)-γ(U))∩int(α,β)-γ(cl(α,β)-γ(V))=int(α,β)-γ(cl(α,β)-γ(U∩V))=cl(α,β)-γ(U∩V), 故cl(α,β)-γ(U)∩cl(α,β)-γ(V)=cl(α,β)-γ(U∩V).
(2)⟹(1) .设U∈T(α,β)-γ,则XU∈F(α,β)-γ,且int(α,β)-γ(XU)∈T(α,β)-γ,由条件(2)可得,cl(α,β)-γ(U)∩cl(α,β)-γ(int(α,β)-γ(XU))=cl(α,β)-γ(U∩int(α,β)-γ(XU))=cl(α,β)-γ(∅)=∅.此外,由定理1可知,cl(α,β)-γ(U)∩cl(α,β)-γ(int(α,β)-γ(XU))=cl(α,β)-γ(U)∩(Xint(α,β)-γ(cl(α,β)-γ(U))),故cl(α,β)-γ(U)∩(Xint(α,β)-γ(cl(α,β)-γ(U)))=∅.从而cl(α,β)-γ(U)⊂int(α,β)-γ(cl(α,β)-γ(U)).另一方面,显然有int(α,β)-γ(cl(α,β)-γ(U))⊂cl(α,β)-γ(U),进而int(α,β)-γ(cl(α,β)-γ(U))=cl(α,β)-γ(U),这样便有cl(α,β)-γ(U)∈T(α,β)-γ,即证X为(α,β)-γ-极不连通空间.
(2)⟺(2*).对于∀U*,V*∈F(α,β)-γ,显然XU*,XV*∈T(α,β)-γ,由条件(2)可知cl(α,β)-γ(XU*)∩cl(α,β)-γ(XV*)=cl(α,β)-γ((XU*)∩(XV*))=cl(α,β)-γ(X(U*∪V*)).此外,由定理1得cl(α,β)-γ(XU*)∩cl(α,β)-γ(XV*)=(Xint(α,β)-γ(U*))∩(Xint(α,β)-γ(V*))=X(int(α,β)-γ(U*)∪int(α,β)-γ(V*)),又cl(α,β)-γ(X(U*∪V*))=Xint(α,β)-γ(U*∪V*),有
int(α,β)-γ(U*)∪int(α,β)-γ(V*)=int(α,β)-γ(U*∪V*).
(2)⟹(3).显然.

另外,由于U,V∈T(α,β)-γ,故U=int(α,β)-γ(U),V=int(α,β)-γ(V),且U∩V=int(α,β)-γ(U∩V),这样cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U))))∩cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(V))))=cl(α,β)-γ(int(α,β)-γ(U))∩cl(α,β)-γ(int(α,β)-γ(V))=cl(α,β)-γ(U)∩cl(α,β)-γ(V).另一方面,cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U∩V)))=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U∩V))))=cl(α,β)-γ(int(α,β)-γ(U∩V))=cl(α,β)-γ(U∩V),因此cl(α,β)-γ(U)∩cl(α,β)-γ(V)=cl(α,β)-γ(U∩V).
(3)⟺(3*).∀U*,V*∈F(α,β)-γ,令U=XU*,V=XV*.
(2*)⟺(4*).显然.
(1)⟹(4).由于X为(α,β)-γ-极不连通空间,则∀U,V∈T(α,β)-γ,有cl(α,β)-γ(U),cl(α,β)-γ(V)∈F(α,β)-γ,由(2*)知
int(α,β)-γ(cl(α,β)-γ(U))∪int(α,β)-γ(cl(α,β)-γ(V))=int(α,β)-γ(cl(α,β)-γ(U)∪cl(α,β)-γ(V))=
int(α,β)-γ(cl(α,β)-γ(U∪V)).
(4)⟹(1).对于∀U*,V*∈F(α,β)-γ,则int(α,β)-γ(U*),int(α,β)-γ(V*)∈T(α,β)-γ,由条件(2)可得,int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U*)))∪int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(V*)))=int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U*)∪int(α,β)-γ(V*)))=int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(U*∪V*)))=int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U*∪V*)))).根据引理1知
int(α,β)-γ(cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U*∪V*))))=int(α,β)-γ(cl(α,β)-γ(U*∪V*))=int(α,β)-γ(U*∪V*).
此外,由定理1可知
int(α,β)-γ(cl(α,β)-γ(U*))∪int(α,β)-γ(cl(α,β)-γ(V*))=int(α,β)-γ(U*)∪int(α,β)-γ(V*),
故
int(α,β)-γ(U*)∪int(α,β)-γ(V*)=int(α,β)-γ(U*∪V*),
根据(2*)即证X为(α,β)-γ-极不连通空间.
(4)⟺(4*).∀U*,V*∈F(α,β)-γ,令U=XU*,V=XV*.
2 (α,β)-γ-超连通空间
定义8设X是拓扑空间,α,β,γ为T的算子,若X的任意非空(α,β)-γ-开集U均为X的(α,β)-γ-稠密子集,则称X为(α,β)-γ-超连通空间.
注2由定义8易知X为(α,β)-γ-超连通空间,则X为(α,β)-γ-极不连通空间.

证明“⟹”.事实上,X的(α,β)-γ-正则空间中仅有两个元素∅,X.否则,假设存在(α,β)-γ-正则开集D⊂X(即D=int(α,β)-γ(cl(α,β)-γ(D))),这里D≠∅,D≠X.易知D为(α,β)-γ-开集,由假设知X为(α,β)-γ-超连通空间,因此int(α,β)-γ(cl(α,β)-γ(D))=int(α,β)-γ(X)=X,这样D=X,故矛盾.

cl(α,β)-γ(U)=cl(α,β)-γ(int(α,β)-γ(cl(α,β)-γ(U)))=cl(α,β)-γ(X)=X,
即U为X的(α,β)-γ-稠密子集,故X为(α,β)-γ-超连通空间.

