砂土与混凝土桩接触界面强度离散元研究

贾 佳

(中铁十九局集团有限公司,北京 100176)

0 引 言

在城市隧道工程、岩土边坡工程及水利工程设计及施工中,桩土相互作用问题常常困扰岩土工作者。针对单一材料,混凝土桩具有强度高、抗变形能力强的特点;由土体材料组成的工程边坡稳定性一般较差。在混凝土桩加固砂土情况下,由于混凝土与砂土存在不连续变形,其力学机制传递极其复杂。桩土界面承担了传递混凝土桩的支护力及砂土变形,对桩土接触面的变形及受力进行研究很有必要。

混凝土桩与砂土接触面目前并无统一法则,国内外学者研究主要集中在室内试验(直剪试验、单剪试验及环剪试验)研究,部分学者进行了理论本构推导及数值模拟。胡黎明等[1]进行了大量混凝土与黏性土剪切面试验,研究了不同粗糙度接触界面力学及变形特性,并提出了离混凝土一定距离剪切带概念。王伟等[2]研究了不同含水率的接触界面剪切应力-剪切位移曲线,建立了法向应力与剪切应力关系,研究发现,法向接触界面满足摩尔库伦定律。殷宗泽等[3]通过升级直剪试验设备,加入位移细观观测装置,研究了混凝土与黏性土接触界面裂纹发展规律,发现桩土界面处裂纹起裂往往从边缘向内部发展。刘杰等[4]针对桩土相互作用,提出了接触界面强度三折线软化模型。任宇[5]通过开发有限元子程序,通过有限元模拟了接触界面变形及受力特性,得到一些可观的结果。石熊等[6]通过室内直剪试验,得到混凝土与红粘土接触界面应力、变形及裂纹扩展模式。杨有莲等[7]研究了直剪过程中,混凝土结构对土体颗粒摩擦属性,发现接触界面会产生一定范围泥皮,对力学及变形影响大。高俊合等[8]建立了混凝土与土体相互作用有限元模型,研究了接触界面应力传递及变形传递规律。

局限于试验设备,目前室内对于砂土与混凝土桩接触面研究主要集中于剪切应力或法向应力-剪切位移研究。传统的有限元主要集中在桩土界面宏观、小变形问题层面,在研究桩土细观、大变形层面局限性较大。颗粒离散元PFC能很好地从细微观及大变形角度揭示岩土体相互作用机制。本文基于颗粒离散元理论,建立混凝土桩与砂土接触面直剪模型,从宏细观、大变形角度,揭示桩土接触面力学传递机制及变形特性。

1 颗粒离散元理论及标定

1.1 颗粒离散元理论

在颗粒离散元理论中,其核心由三部分组成,分别为圆颗粒(ball)、墙单元(wall)及接触(contact)。由于实际工程中,颗粒轮廓线和可破碎性对力学及变形影响很大,学者基于圆球颗粒分别提出了不考虑变形考虑形状不规则性的刚性簇单元(clump)以及既考虑变形破坏又考虑形状的不规则性的柔性簇单元(cluster)。

颗粒离散元理论中,颗粒或簇单元之间满足牛顿第二定律;接触(颗粒与颗粒接触,颗粒与墙单元接触)之间需满足力-位移准则。

(1)力-位移准则

颗粒离散元模型中,作用于接触模型的力由切向接触力和法向接触力组成:

结合本构模型,可得到作用于颗粒上的合力及合力矩。

(2)运动法则

通过力-位移准则确定了作用于颗粒上的合力和合力矩,而后,根据运动法则,可建立颗粒平移和旋转运动方程:

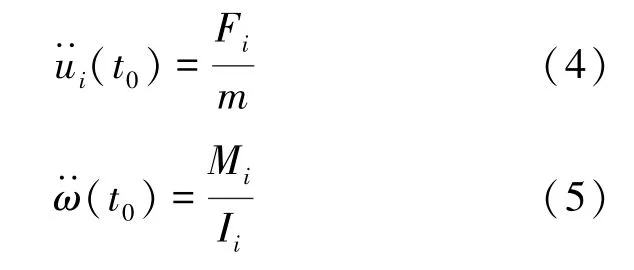
线性接触模型力学响应见图1,颗粒在上一时步的力的作用下产生位移,结合力-位移准则及接触的本构模型计算得到作用于颗粒上的新的合力及合力距;有了颗粒上的合力及合力矩,通过运动法则,建立平行加速度及角速度与合力及合力矩关系,可得到颗粒的更新后的位置及旋转信息,如此反复计算,实现模型的大变形破坏[9]。

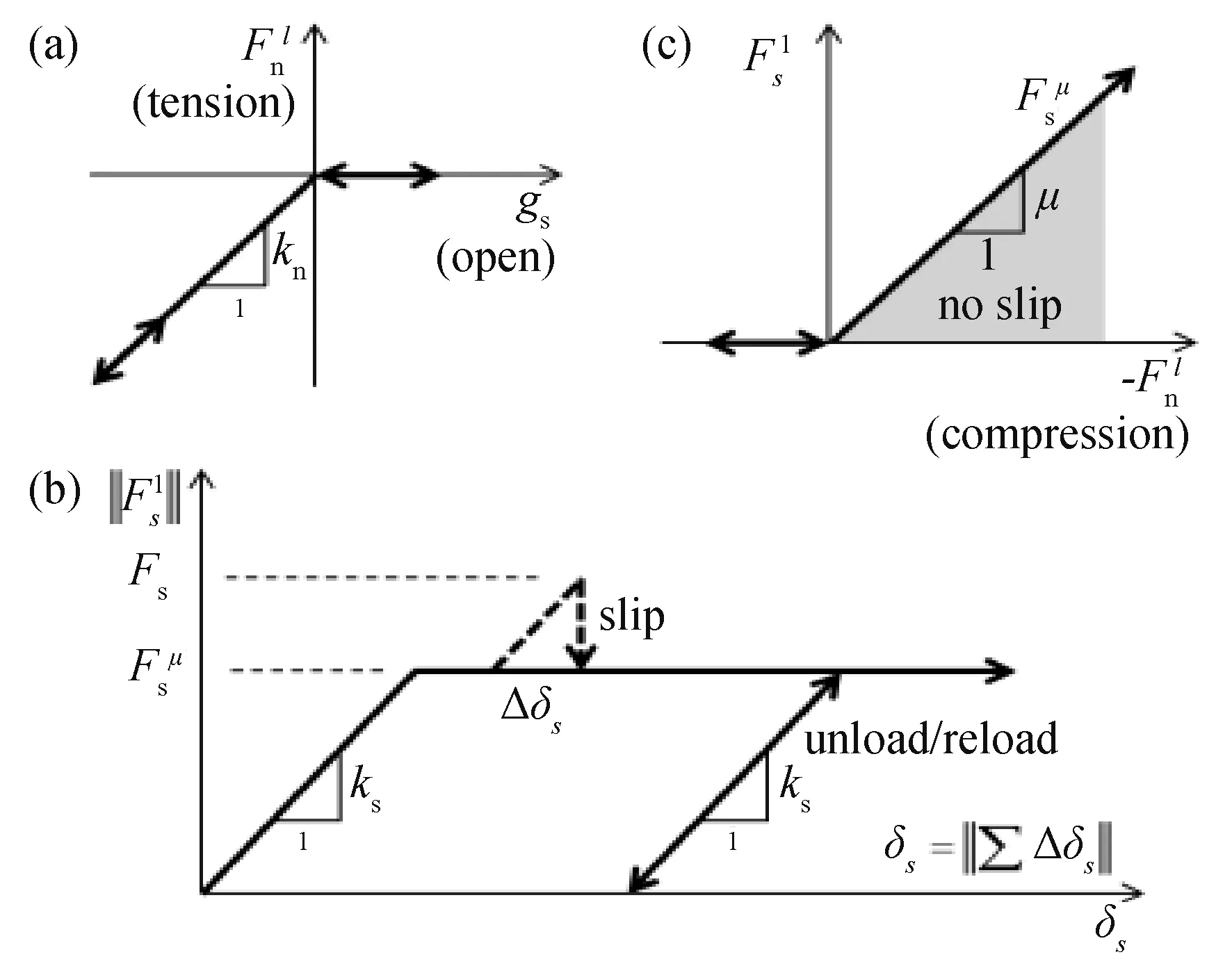
图1 线性模型接触本构

1.2 细观接触参数确定

通过PFC2D双轴试验确定砂土细观强度参数,DEM试样尺寸、物理参数如下:建立100 mm×50 mm的DEM双轴压缩试样,综合考虑计算效率,选取最大颗粒径、最小颗粒粒径分别为0.98 mm、0.30 mm,试样密度为1.98 g/cm3,孔隙比为0.15,级配曲线见图2。

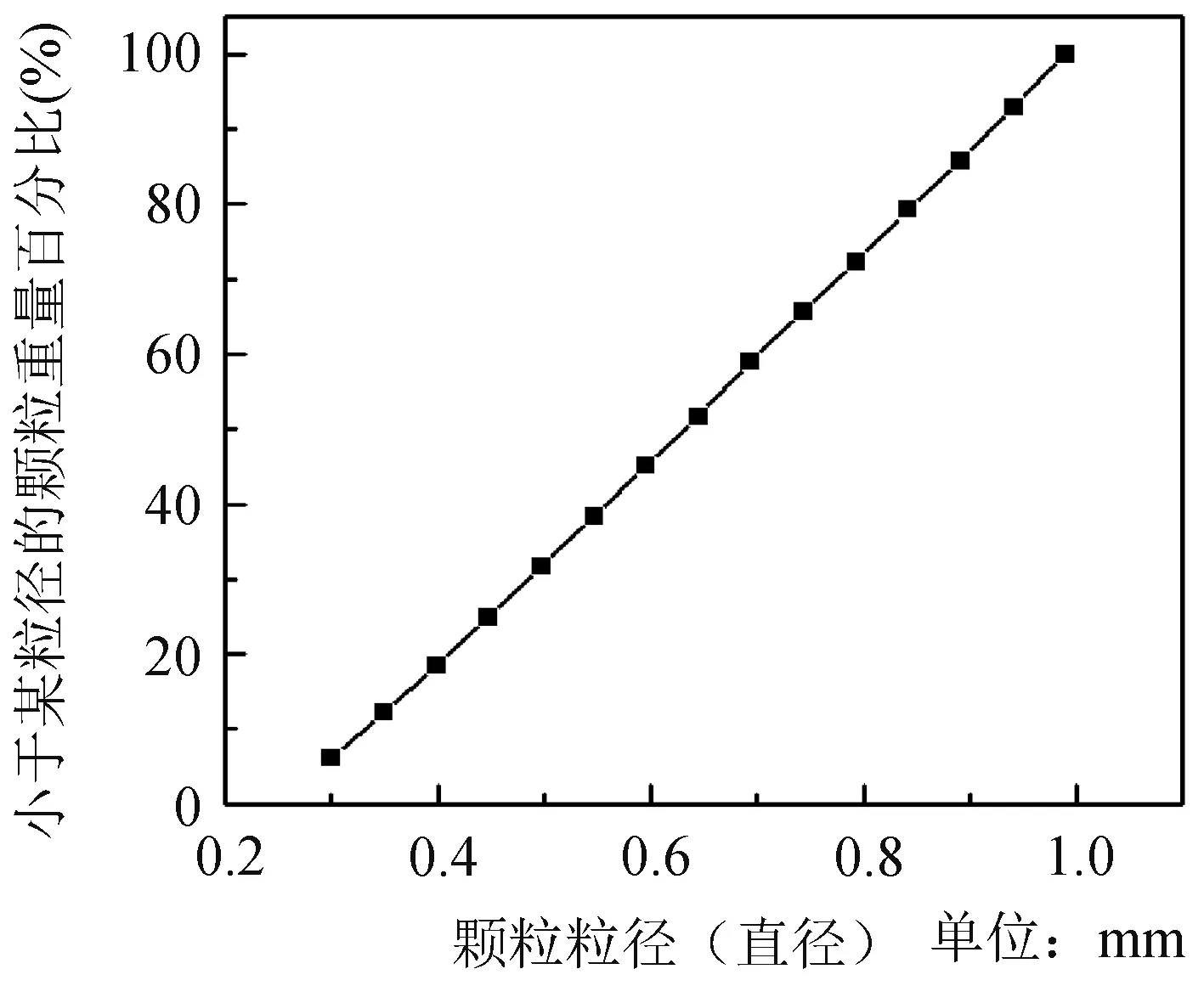
图2 砂土颗粒级配曲线

砂土、混凝土界面采用线性接触模型,需确定的细观参数有接触模量、法向接触刚度、切向接触刚度及摩擦系数。学者研究发现,线性模型接触模量及法向接触刚度与宏观弹性模量细观性较高,主要影响砂土的变形;切向接触刚度与摩擦系数与宏观的内摩擦角相关性较高,主要影响剪切曲线峰值[9]。

双轴试验围压分别为50 kPa、150 kPa及300 kPa,砂土双轴破坏模式及应力-应变曲线见图3,双轴模型剪切破坏呈双剪破坏模式,砂土局部滑动严重。通过双轴压缩试验得到混凝土桩及砂土的线性模型细观参数,见表1。

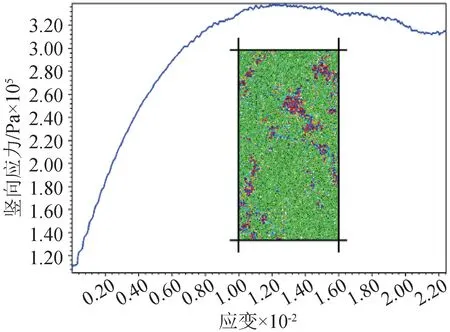
图3 砂土双轴破坏模式及应力-应变曲线

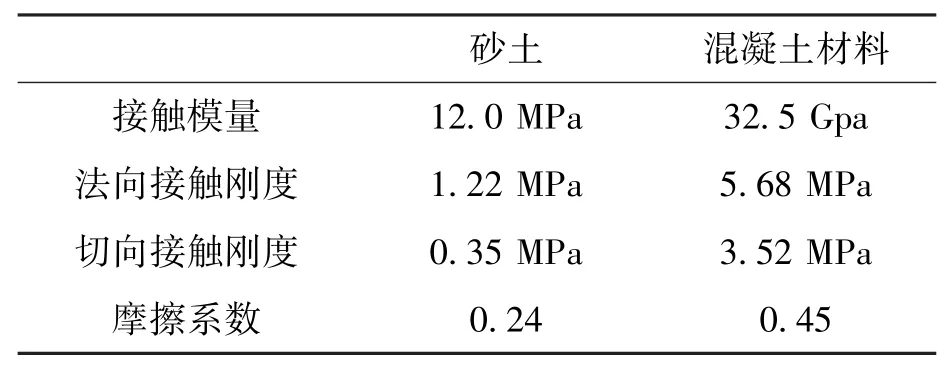
表1 土体及混凝土结构细观强度参数

2 直剪离散元模型建立

建立的混凝土桩与砂土相互作用直剪模型见图4。模型长200 mm×高100 mm,直剪模型中,桩基采用不考虑其变形及破坏属性的clump模拟;上部墙体通过伺服加载模式,上覆荷载为100 kPa。建模过程及直剪试验过程如下:

(1)混凝土桩建模,通过PFC2D内置fish语言,遍历桩基颗粒pebble位置及半径信息,基于clump template 生成桩基模板,赋予上述标定的线性模型参数,还原混凝土桩强度属性;

(2)上覆荷载施加,基于颗粒离散元理论,通过不断检索上部加载墙体刚度及应力,不断更新上部墙体施加速度,即伺服作用,实现伺服荷载在直剪过程中保持100kPa目标值不变;

(3)设置监测变量,监测混凝土桩剪切应力及剪切位移。在直剪模型中间位置,沿混凝土桩高度10 mm、20 mm、30 mm、40 mm、50 mm设置水平位移监测点hdisp_1、hdisp_2、hdisp_3、hdisp_4、hdisp_5,见图4。并全局设置测量圆,监测应力及最大、最小主应力;

(4)桩基以0.01 mm/min水平速度剪切。通过设置的监测点,得到接触界面宏细观、大变形下的力学机制、变形情况,下述从剪切应力-剪切位移曲线、位移矢量及应力矢量等揭示桩土相互作用力学机制及变形情况。

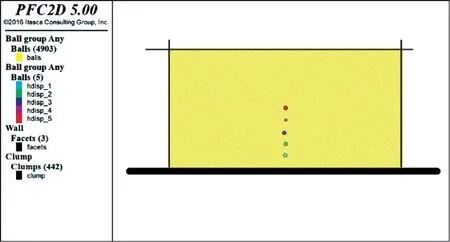
图4 直剪DEM模型及位移监测点

3 直剪计算结果分析

3.1 数值模拟与试验结果对比

图5为不同上覆荷载下数值模拟剪切应力-剪切位移曲线。当上覆荷载为50 kPa时,剪切峰值约为32 kPa,随着剪切位移继续增加,峰值出现软化。由于本文砂的粗糙度偏低,在荷载较小时,加载后期颗粒发生偏转,剪切应力有所降低,因而曲线出现软化现象。当上覆荷载为100 kPa时,峰值强度约为115 kPa,颗粒抗转动能力增加,峰后曲线呈现平曲线形态,滚动摩擦效应明显。当上覆荷载为200 kPa时,峰值荷载达到约160 kPa,峰后硬化现象明显。综上所述,剪切应力随着上覆荷载增大而增大,颗粒抗偏转效应增强。

图6为不同上覆荷载下室内试验剪切应力-剪切位移曲线。随着上覆荷载增加,剪切强度增大,峰值位移向后推移,规律与数值模拟基本一致。当上覆荷载为50 kPa、100 kPa、200 kPa时,室内试验与数值模拟剪切峰值强度相差分别为7.2%、8.3%、8.8%,数值模拟与室内试验结果基本一致,说明颗粒离散元PFC模拟桩土剪切合理性。

图5 不同上覆荷载下数值模拟剪切应力-剪切位移曲线

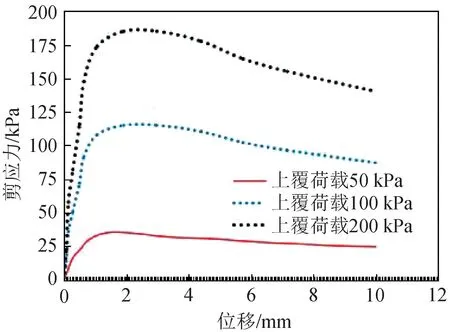
图6 不同上覆荷载下室内试验剪切应力-剪切位移曲线

3.2 混凝土桩基剪切应力-剪切位移特性分析

混凝土桩剪切应力-剪切位移曲线见图7,曲线有匀速增长、减速增长及下降三阶段,分别对应弹性变形阶段、硬化阶段及软化阶段。下述从接触界面层面分析三阶段对应的力学机制及变形情况。

(1)弹性变形阶段。当剪切位移较小时,在上覆荷载作用下,土体试样竖向压密,图8为土体竖向位移-剪切位移曲线,在剪切位移较小(0.26 mm内)时,上部墙体向下压密试样。小剪切变形阶段,混凝土桩与砂土接触界面在静摩擦作用下,剪切应力随剪切位移线性增长,此时砂土颗粒旋转较小。

(2)强度硬化阶段,当剪切位移达到0.3 mm时,随着剪切位移增大,剪切强度增长速率降低,同时上部墙体向上运动,表现为典型剪涨作用,图9为砂土颗粒旋转作用云图,可以发现在强度硬化阶段,桩土接触界面处颗粒旋转作用明显,并且旋转由接触面向砂土内部传递,离混凝土桩较近距离处砂土旋转角度普遍在5°左右。当剪切位移在0.3~0.8 mm之间时,砂土出现硬化现象。

(3)强度软化阶段,当剪切位移大于0.8 mm时,剪切强度开始下降,剪切位移达到1.60 mm时,剪切强度降低到一个稳定值32 kPa。从竖向位移-剪切位移曲线可知,此时砂土仍处于剪涨状态。由于接触界面处砂土颗粒在较大剪切变形作用下,从动摩擦状态转化为旋转状态,导致界面剪切应力快速降低,同时旋转对上部土体挤压作用明显,带动了离混凝土桩一定距离砂土旋转。当剪切位移达到1.60 mm时,离混凝土桩接触界面一定范围内砂土在混凝土桩带动下,摩擦效应基本被颗粒旋转效应代替,剪切应力维持在较小稳定值。

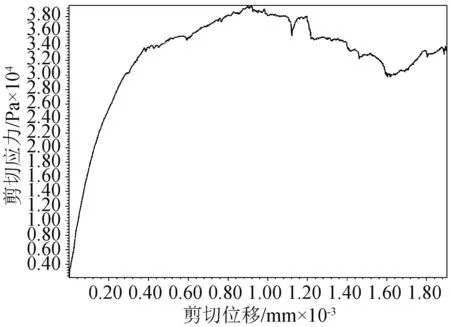
图7 剪切应力-剪切位移曲线

图8 竖向位移-剪切位移曲线

图9 竖向位移-剪切位移曲线

3.3 颗粒位移矢量特性分析

下文从位移矢量角度揭示接触界面变形特性,剪切过程中,桩土接触界面位移矢量见图10。当剪切位移为0.15 mm时,砂土处于弹性变形阶段,砂土主要以水平位移为主,上部砂土保持较小的向下运动趋势,对应竖向位移-剪切位移曲线压密阶段,桩土并未发生相对运动。在静摩擦作用下,混凝土桩带动离桩焦较小距离砂土运动。当剪切位移达到0.70 mm时,离混凝土桩较近处砂土位移达到0.61 mm。混凝土桩处砂土位移以水平位移为主,离桩一定距离位置,以向上竖向位移为主,试样剪涨作用明显。当剪位移达到1.90 mm时,砂土最大水平位移达到1.52 mm,砂土向上运动作用明显,桩土接触界面处砂土旋转作用明显。

图10 剪切过程位移矢量图

沿混凝土桩高度方向水平位移-剪切位移曲线见图11。在小剪切位移状态下,不同高度范围处砂土水平位移差别不大,试样处于静摩擦状态,当剪切位移达到0.40 mm时,离混凝土桩越远,其水平位移越小,桩对砂土的水平约束作用越小。

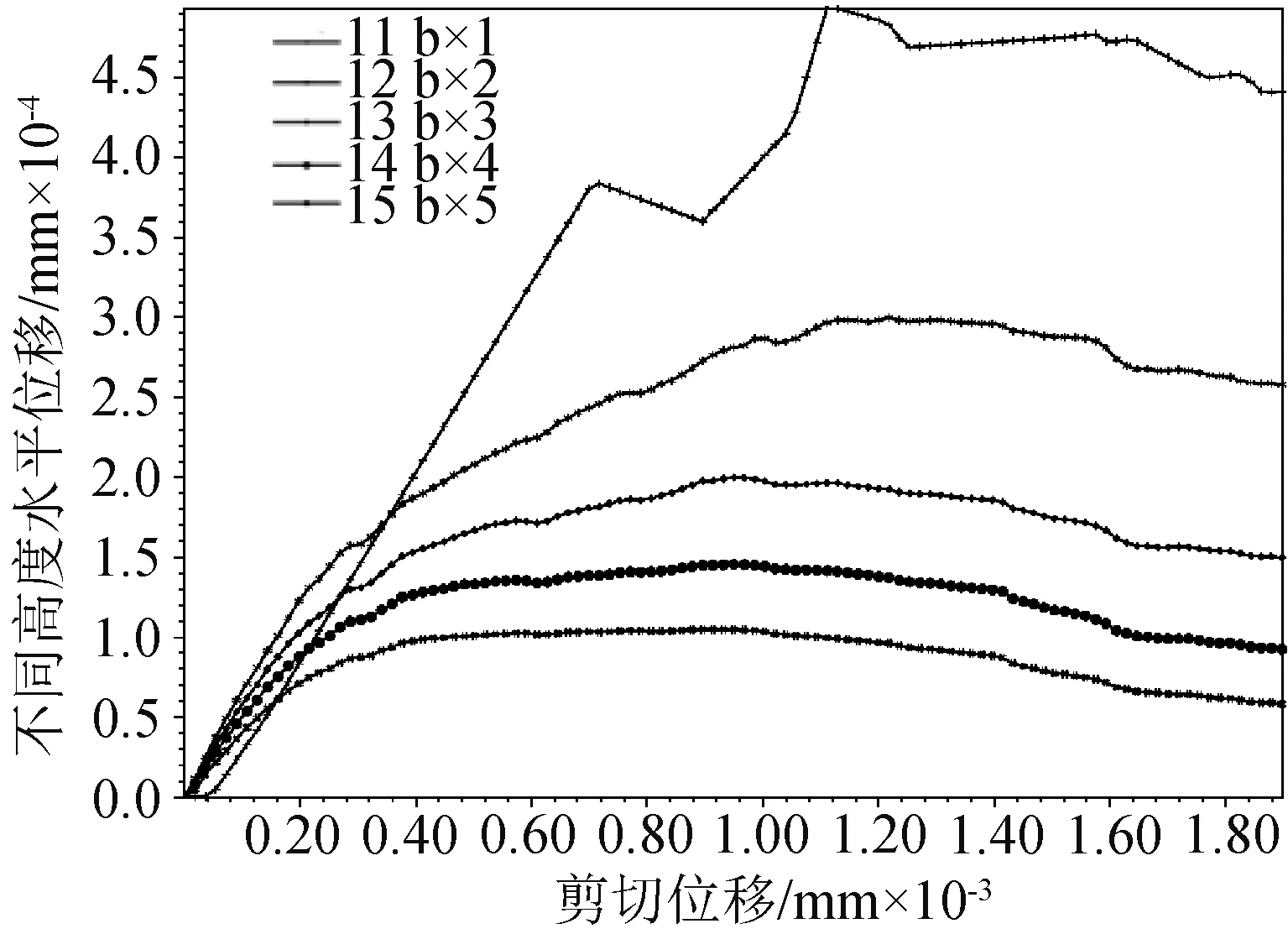
图11 沿高度方向水平位移-剪切位移曲线

综上所述,小剪切位移状态下,混凝土桩与砂土界面相对变形较小,接触界面在静摩擦作用下随桩发生弹性变形。随着剪切位移增大,桩与砂土界面出现滑动,砂土出现较大剪涨作用。剪切位移达到1.90 mm时,桩土接触处颗粒出现旋转,混凝土桩剪切运动对砂土剪涨作用影响明显,对砂土内部颗粒水平位移影响有限。3.4 力学特性分析

砂土内部最大、最小主应力矢量见图12。当剪切位移为0.15 mm时,在上覆荷载作用下,最大主应力主要沿竖直方向,最小主应力沿水平方向。当剪切位移达到0.70 mm时(试样处于强度硬化阶段),最大主应力与水平方向成10°,在剪切方向端部出现应力集中现象,剪切方向后部应力偏转效应较弱。当剪切进入软化阶段时,剪切端部应力进一步集中,最大、最小主应力有一定程度降低。

图12 剪切过程最大最小主应力矢量图

4 结 论

(1)基于颗粒离散元理论,确定了混凝土桩、砂土线性接触细观参数,应用于桩土剪切模型中,得到了剪切应力-剪切位移曲线弹性变形、强度硬化、强度软化三阶段破坏特性。

(2)剪切过程中,小剪切位移状态下,桩土接触界面在静摩擦作用下处于弹性变形状态。随着剪切位移增大,桩与砂土界面出现滑动,砂土出现较大剪涨作用。随着剪切位移增大,砂土从动摩擦状态转化为旋转状态,导致界面剪切应力快速降低,对土体剪涨作用明显。

(3)剪切过程中,最大主应力由竖直方向向水平方向偏转。在剪切方向端部出现应力集中,剪切方向后部应力偏转效应较弱。当剪切进入软化阶段时,剪切端部应力进一步集中,最大、最小主应力有一定程度降低。