新常态下的均衡汇率和央行干预——兼论汇率失衡的动态演变机制

杨杰 冯芸

内容提要：伴随着人民币汇率形成机制改革的逐渐深化和国际国内经济环境的复杂变化，基于不变系数的行为均衡汇率模型的均衡汇率研究已然无法反映经济结构的动态变化。鉴于传统回归均值系数的不足，通过分别建立半参数变系数形式的行为均衡汇率模型和半参数变系数部分线性形式的误差修正模型，依次深入分析了各基本经济因素的时变影响和人民币汇率自我调节能力的动态变化。并进一步通过平滑转移自回归模型实证检验了央行干预与人民币汇率失调的关系，并创新地采用非齐次隐马尔可夫自回归模型深入研究了人民币汇率失调的动态演化机制。研究结果表明：人民币汇率不存在较大程度的失调，变系数模型能更好地反映各经济变量因素的动态影响；人民币汇率的自我调节修正能力表现出周期性振荡起伏的趋势，审慎择时的汇率机制改革能够有效地强化人民币汇率的自我调节能力；在绝大部分时间央行干预推动了人民币汇率均衡，促进人民币汇率逐步回归经济基本面；人民币汇率失调存在显著的不对称性，人民币汇率均衡态的自维持概率呈现出不断增加的趋势。

一、 引 言

在开放经济下，汇率一方面作为重要的涉外经济变量影响一国的对外收支平衡，另一方面也作为国家宏观经济的主要调控手段和经济杠杆影响国民经济发展。中共十八大以来，随着中国经济进入“新常态”时代，人民币汇率在汇率波动限制放宽和汇率中间价的形成方式改革的影响下，出现了人民币贬值预期膨胀、双向波动和升贬值阶段性交替出现的新态势(田开兰等，2017；许从宝等，2020)。汇率的走势受到其比价属性的约束，在比价属性下，其他宏观经济变量，例如货币供给量、国际收支等会影响汇率水平。一个判别汇率是否高估或者低估的方法是估计实际汇率和均衡汇率的差，只有充分地了解均衡汇率的变动趋势才能更有效地进行汇率管理。

尽管中国央行明确表示汇率政策的目的在于保持人民币汇率在合理均衡水平上基本稳定，但美国财政部仍多次将中国列为“汇率操纵国”，最近的一次发生在2019年8月，这种“政治化”的认定和指控属于任性的单边主义和保护主义行为，严重破坏国际规则，对中美两国贸易乃至全球经济金融都产生了重大影响。“汇率操纵国”是指不顾本国经济基本面，人为操纵汇率以达到牺牲别国利益从而使本国贸易受益的行为。而中国央行干预仅是为了实现一个健康的、不脱离基本面并围绕均衡水平波动的汇率动态调整机制，这是反击“汇率操纵国”指控的有力事实。因此测算人民币汇率失调程度，并在此基础上研究央行干预和汇率间的关系，深入探讨人民币汇率失调和均衡的内部动态演化机制就显得格外重要。

均衡汇率是指在无过度失业、国际贸易和资本流动无特别限制或鼓励的前提下使得国际收支达到均衡的汇率，均衡汇率对一国宏观经济的稳定运行和可持续发展有着至关重要的意义。在早期研究中，均衡汇率大多基于购买力平价(PPP)理论进行测算。随后均衡汇率理论的研究得到了长足的发展，且自成体系，像重视内外均衡的基本要素均衡FEER理论(Williamson，1983)、单一简约方程的行为均衡汇率BEER理论(Clark和MacDonald，1999)、针对中长期汇率的自然均衡汇率NATREX理论(Stein，1994)以及强调发展中国家转型经济特点的均衡实际汇率ERER理论(Edwards，1989；Elbadawi，1994)等等。其中，BEER模型由于其可操作性、灵活性以及更贴近现实的指导意义，受到很多学者的青睐。国内学者中，最早采用BEER模型对人民币均衡汇率进行测算的是张晓朴(1999)，他结合了FEER和BEER两个方法的基本思想，发现人民币汇率在1984年初至1985年末及 1989年初至1990年末被高估，而1987年初至1988年末及1998年上半年被低估。随后很多国内学者都通过BEER模型对均衡汇率进行了探讨，比如吴丽华和王锋(2006)、黄万阳(2013)、姚宇惠和王育森(2016)等等，此类文献较多，不再一一列举。

值得注意的是，上述文献中均采用均值系数回归的协整方程测算均衡汇率，得到的是经济因素对均衡汇率的平均影响。随着人民币汇率形成机制改革的不断深化，这种传统的计量模型已经不足以反映诸影响因素变化对均衡汇率的动态影响，不过这个方向的研究甚少。项后军和潘锡泉(2010)认为宏观经济政策的改变会使得汇率数据生成过程发生结构性突变，直接忽略结构突变进行的均衡汇率测算会存在偏误，因此他们运用Bai-Perron内生多重结构突变检验方法和结构突变协整方法对均衡汇率和汇率失调程度进行测算，并在向量误差修正模型中引入代表结构突变点的虚拟变量，仍发现汇率自我修正动态调整机制的存在；孙章杰和傅强(2014)建立了反映中国经济结构动态变化的时变系数BEER模型，通过在线性协整方程中引入状态空间结构，得到了各主要经济影响因子对人民币汇率的动态影响。虽然孙章杰和傅强(2014)构建的状态空间BEER模型已达到了考察各个经济因素长期动态影响的目的，但是他们设定的状态方程服从一阶AR过程，这种严格的模型设定形式可能会限制研究各自变量对均衡汇率的非线性影响，这也是状态空间模型在模型设定时存在的不足之处。

其次，鲜有文献在汇率失调的测算结果上，进一步深入研究人民币汇率失调的时变转换机制。陈华(2013)认为央行干预对汇率失调存在U型效应，使用ESTAR模型实证检验了人民币汇率错位程度的变化过程。他发现，人民币汇率失调程度存在着两个性质截然不同的区制：在“非均衡”区制下，央行干预对人民币汇率的均衡产生阻碍，汇率错位程度不断扩大；而在“均衡”区制下，人民币汇率收敛于均衡水平，央行干预促使人民币汇率更加均衡。文中指出除少数时间点外，在绝大部分时期央行干预对人民币汇率均衡都起到了积极的促进作用。不过考虑到他研究时所采用的数据已较为久远，仅至2013年，另一方面他也并未进一步深入探究人民币汇率失衡内部的动态演化机制，因此本文一方面在最新数据集上检验近些年来央行干预对人民币汇率均衡的促进作用，另一方面进一步创新地采用非齐次隐马尔可夫自回归模型深入探究汇率低估、高估和均衡之间的时变转换过程。

本文将在BEER模型的协整方程基础上引入半参数变系数理论，就我们所知，在研究人民币均衡汇率的领域本文是最早应用该方法的。通过这种更加灵活的半参数模型，可以准确地刻画各个宏观经济变量在不同时期对人民币汇率的动态时变影响，并且经过该改进模型所测算出的均衡汇率和汇率失调程度也更加准确严谨，符合现实的经济分析。同时在以往的人民币均衡汇率的误差修正模型中，通常也是以不变系数考察人民币汇率的自我修正能力，这其实是不太准确的，随着中国经济结构的变化和汇率体制改革的不断深化，人民币汇率对短期偏离的修正能力并不是一成不变的，因此本文将采取半参数部分线性形式的误差修正模型，以改进现有研究的缺陷。进一步地，基于最新的数据集，本文通过指数型平滑转移自回归模型检验和评价了央行干预在汇率均衡和汇率失调两区制之间所起的关键作用，并以央行干预指数作为外部协变量，创新地采取非齐次隐马尔可夫自回归模型详细审视了人民币汇率失衡的动态演化机制，这为研究汇率失调提供了一个全新的视角，可为之后的相关研究提供借鉴。

本文随后的行文安排如下：第二节介绍模型设定以及相关变量的选择，第三节测算人民币汇率错位程度并进行相关的详细分析，第四节检验央行干预对人民币汇率的促进作用，第五节研究人民币汇率失衡的动态演化机制，第六节给出研究结论和相关的政策建议。

二、 模型设定和变量选择

1.BEER半参数变系数模型设定

行为均衡汇率理论(Behavioral Equilibrium Exchange Rates)是1998年Clark和MacDonald基于基本要素均衡汇率理论(FEER)提出的，BEER模型采用一个简约单方程来测算均衡汇率，它解决了FEER模型过于理想化，可操作性差的缺陷。

行为均衡汇率模型区分了均衡汇率影响因素中的长期、中期和短期成分，其基本表达式为：

(1)

其中，qt是实际有效汇率(Real Effective Exchange Rate，REER)，X1，X2，T分别是长期、中期和短期影响因素，β1、β2和β3是各简约式系数的向量，εt是随机扰动项。

根据估计出的系数，可以计算长期的均衡实际汇率(Equilibrium Real Exchange Rate，ERER)：

(2)

定义总汇率失调水平(Total Misalignment，tm)为：

(3)

从式(3)可以直观地发现，长期汇率失调被分解成了三个部分：长中期经济因素自身的失调、短期临时性因素和随机性因素。这样的定义使得BEER模型在实际操作中，可以方便而快速地认清汇率失调的性质，便于政府决策对症下药。

一般地，通过下式对汇率错位(Exchange Rate Misalignment，MIS)程度进行测算：

(4)

本文将通过半参数变系数模型对BEER模型进行拓展。Hastie和Tibshirani(1993)提出了半参数变系数模型：

(5)

其中E[εi|Xi,Zi]=0，变系数函数β(Z)=(β1(Z),β2(Z),…,βp(Z))是q维向量Z未知向量值光滑函数，Xi=(Xi1,Xi2,…,Xip)T，第一个分量为1，在X影响Y的过程中Z起到了调节作用。在BEER模型中，可以选取时间作为变量Z。

变系数模型通常采用局部多项式的估计方法，其中比较常用的是局部线性估计，与高阶多项式相比，其待估参数较少，且效果并不输于高阶多项式。一般而言，核函数的选择对估计结果影响较小，因此本文选取常用的Gaussian核函数，而且在估计过程中，最佳窗宽通过最小二乘交叉验证法(Least Squares Cross-validation，LSCV)来确定。

2.变量选择

本文在借鉴Clark和 MacDonald(1999)提出的解释变量的基础上，参考国内学者研究，并根据中国国情需要加入部分变量，但对不可得变量采用剔除或替代的方法，最后选择出初始变量集，简介如下。

人民币实际有效汇率指数(REER)：为了衡量人民币实际汇率，选取国际清算银行(BIS)测算发布的宽口径指数作为人民币实际有效汇率，为被解释变量。该指数每月更新一次，且根据贸易信息等对汇率的权重进行了适当的调整，更加符合国内的经济情况。BIS对汇率采用间接标价法，因此实际有效汇率的上升(下降)意味着人民币的升值(贬值)。

劳动生产率(GDP/TNT)：劳动生产率的提高会使本国商品在国际上的相对价位降低，增强本国商品的国际竞争力，致使商品的出口更加容易；随着本国贸易收支状况的改善，会使本国的实际汇率升值。因此劳动生产率对实际有效汇率会产生正向影响。劳动生产率指标常被分为直接指标和间接指标。直接指标直接衡量生产率增长的趋势，但中国缺少相关的权威统计数据，因此大部分学者选择使用替代变量，诸如：GDP、人均GDP、中国人均GDP/美国人均GDP(经过汇率换算)、GDP增长率等等。本文选取月度GDP作为衡量劳动生产率的直接指标，月度GDP数据通过Litterman 频率转换方法(张春华等，2017)对季度GDP数据插值得到。间接指标试图抓住体现Balassa-Samuelson效应(以下略称“B-S效应”)的贸易品部门与非贸易品部门生产率增长的差异。理论上该指标需要非贸易品和贸易品的价格指数去计算，但在实际操作中我们无法得到这两个价格指数。故遵从文献的普遍做法，使用生产者价格指数(PPI)或批发价格指数(WPI)来描述贸易品的价格变化,使用消费者价格指数(CPI)来描述非贸易品的价格走势，即TNT=CPI/PPI。

广义货币供应量(M2)：反映一国的货币政策和经济货币化的程度，一般而言货币供给增加会导致本币贬值。

贸易开放度(OPEN)：该变量反映了一国贸易自由化和对国际市场依赖的程度，我们用外贸依存度即进出口总额占GDP的比例来表示。一般而言,开放度与实际有效汇率成反向关系，开放度上升会使进口增加、经常账户恶化，为维持外部均衡，实际有效汇率贬值。

贸易条件(TOT)：本文以出口总额与进口总额之比表示，比值上升，则该国贸易条件改善，反之贸易条件恶化。贸易条件的改善对实际有效汇率的影响取决于其收入效应与替代效应，其最终的综合效应并不确定。

外商投资占GDP的比重(FDI)：FDI是中国资本金融项目顺差的主导因素，外商直接投资增加会导致本币升值。

政府支出占GDP的比重(GOV)：一般而言，政府财政支出增加时，对货币的需求也相应地增加，若货币供给不变，利率上升，实际汇率升值。

外汇储备(FORE)：外汇储备的增加，表明贸易顺差的增加，且该国可从外部获得更多的投资收益，这会增加经常账户盈余，因此预期外汇储备与实际有效汇率的变动正相关。

以上数据均来源于wind数据库。文章实证分析选取的时间跨度为2006年1月至2020年12月，样本容量共180个。本文使用月度数据克服了以往文献大都采取季度、年度数据容量过小，数据质量不高的缺点。所有变量均通过季节调整和取对数的处理。

三、 人民币均衡汇率和汇率错位实证研究

在对各变量进行协整检验之前，需要进行ADF单位根检验，检验结果见表1。

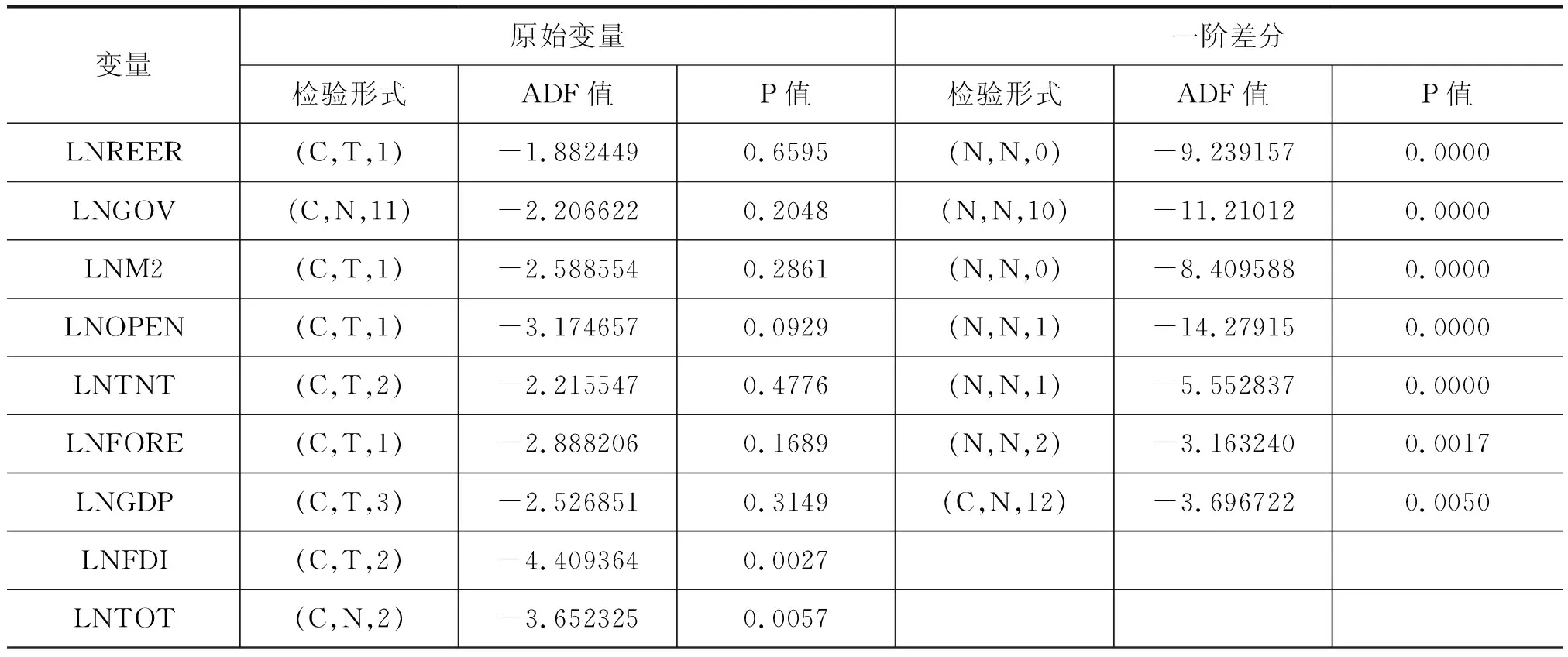
表1 ADF单位根检验结果

从表1检验结果可以看出，LNFDI和LNTOT原序列已平稳，其他变量的原序列均不平稳，但一阶差分序列在1%显著性水平下都拒绝原假设，即均为I(1)过程。因此排除掉LNFDI和LNTOT。同时还发现，LNGDP和LNTNT相关性较大，因此将LNGDP也删除。所以本文最终所采用的BEER实证分析模型是：

(6)

1.人民币实际汇率的传统BEER模型

在前文的基础上，可以进一步进行协整检验。基于各判别准则(FPE准则、AIC准则、SC准则和HQ准则等)可以确定VAR模型的最佳滞后期为2阶。对VAR(2)模型进行稳定性检验，见表2，可以发现没有单位根位于单位圆外，表明VAR(2)模型满足稳定性条件。建立VAR(2)模型后进行Johansen协整检验，检验结果见表3。

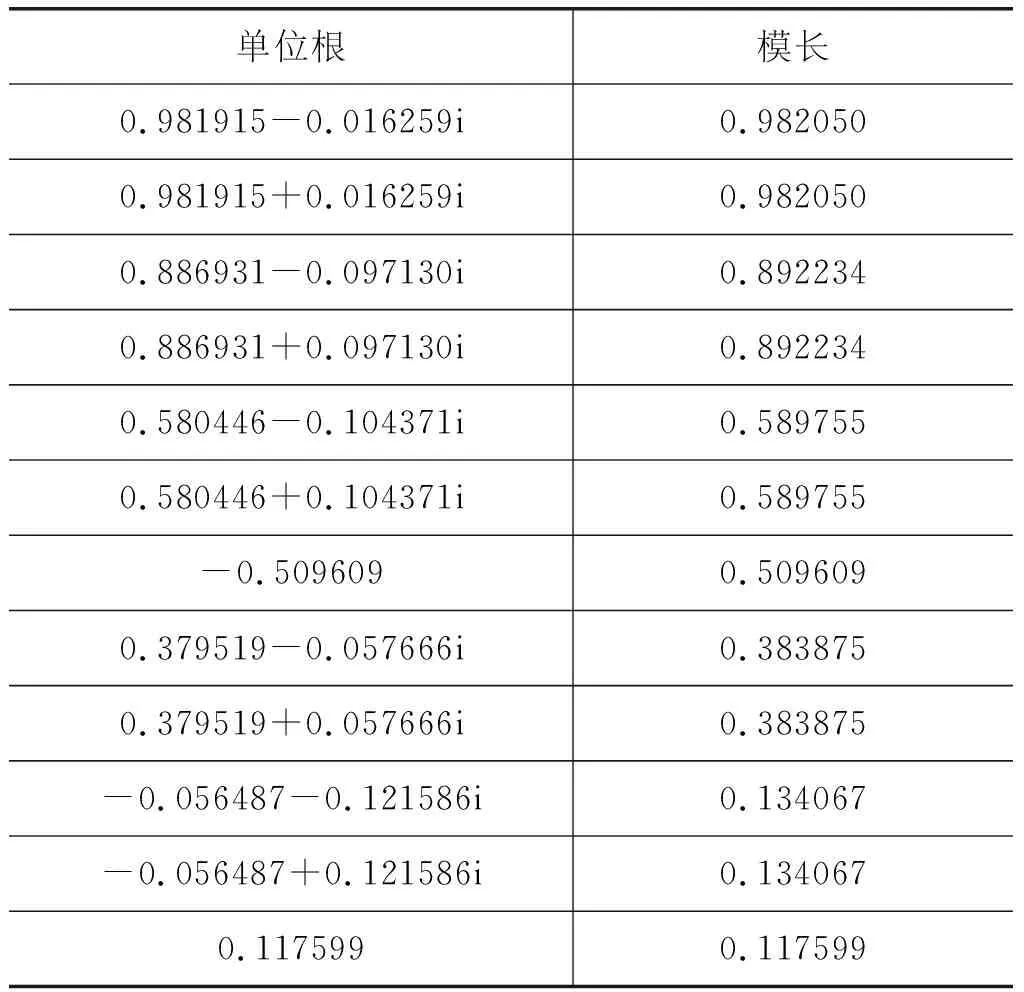
表2 VAR模型稳定性检验

协整检验结果显示，变量之间存在着长期稳定的协整关系，并且可以得到所估计的协整方程(系数下方圆括号中表示标准差，方括号中表示t值，下同)：

(7)

对协整方程的残差进行平稳性检验，发现残差已是平稳序列，并且在0附近波动，验证了协整关系的正确性。从上方方程中各变量的系数可以看出，系数的正负方向和之前预期分析的结果基本一致，即间接劳动生产率的提高、外汇储备和政府财政支出的增加会致使实际汇率上升；而货币供应量的增加和贸易开放度的提高会引起实际有效汇率的下降。

进一步建立描述人民币实际汇率动态调整机制的向量误差修正模型，估计结果如下：

(8)

其中，误差修正项ECM为：

ECM=LNREER(-1)-0.07271LNFORE(-1)-0.43636LNTNT(-1)+1.19999LNM2(-1)+0.04800LNOPEN(-1)-0.02663LNGOV(-1)-7.59950

(9)

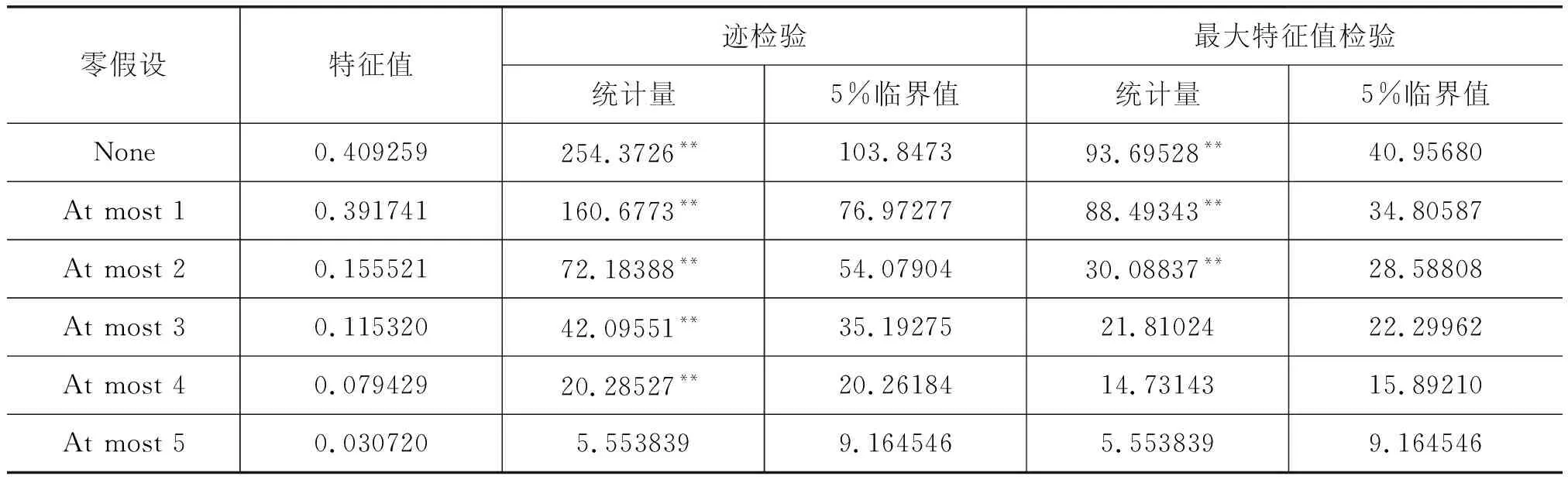
表3 Johansen协整检验结果

误差修正项ECM的系数的大小反映了人民币实际有效汇率偏离长期均衡值时，向长期均衡值调整的速度，即人民币汇率的自我修正能力。从估计结果中可以看到，ECM的系数为-0.01814，这表明在样本期间，人民币汇率具备一种在长期能够自我逐步返回平衡的负反馈机制，也就是说人民币汇率失调可以得到经济系统的自动修复。但是，可以看到该系数绝对值较小，说明人民币汇率误差修正机制的自我修正能力比较有限，当汇率低估或高估的程度较大时，一方面需要不断增强汇率的自我修正机制，另一方面也需加以政府的宏观调控，才能使实际有效汇率逐渐趋于均衡水平。

不过，正如前面所提到的，BEER协整方程中各经济因素的系数反映的只是样本期间的均值影响，无法体现出随着中国经济结构的改变和汇率体制改革的深化，各经济变量对人民币汇率的动态影响。同理，向量误差修正模型中误差修正项的系数也体现的是样本期间人民币汇率的平均自我修复能力，直觉上来说这种自我修复能力的大小也应当是随着中国经济发展和汇率改革而不断变化的。因此在下文，将分别在BEER协整方程和向量误差修正模型中引入半参数变系数理论和半参数部分线性模型，后者着重用来刻画人民币汇率自我修正机制随时间变化的趋势。

2.半参数变系数BEER模型

上文中已确认变量间协整关系的存在，接下来考虑在维持变量线性协整关系的基础上，引入半参数变系数结构，可以得到需要估计的半参数变系数协整方程如下：

LNREER=β1(t)+β2(t)LNFORE+β3(t)LNTNT+β4(t)LNM2+β5(t)LNOPEN+β6(t)LNGOV

(10)

上式(10)中选择时间t作为变系数的自变量，并且t经过min-max归一化处理。通过局部线性估计可以得到各自变量时变系数的估计。下图1给出各经济影响因素的时变系数图，其中纵轴方向的曲线，是由核密度估计得到的各时变系数的概率密度函数。

由图中可见，变系数模型中所有经济因素的影响水平随时间都发生了很大的变化，并且可以看出这些变化都是非线性的，说明在不同的经济发展阶段，随着汇率制度改革的不断深化，外汇储备、间接劳动生产率(B-S效应)、货币供应量、贸易开放度和政府支出对人民币实际汇率的影响程度不断发生变化。

显然，相比单纯的不变系数线性模型，半参数变系数模型提供了更加丰富的信息。观察图1可发现，外汇储备对人民币汇率的影响虽然在不同时间有所不同，但基本都保持在0.3以上，表明外汇储备的增加，给予了人民币汇率较大的升值压力；而反映B-S效应的间接劳动生产率的系数经历过初期短暂的负值之后基本稳定在0.2～1.2之间；广义货币供应量对实际汇率的影响一般而言是负的，不过图中曲线显示时变系数的走势是正负交替的，这与直觉上的预期不符，但这并非有误。管涛(2018)表示人民币并不存在因“货币超发”而必然贬值的逻辑，而且他认为中美两国M2的口径存在差异，并且两国M2总量差距的主要原因是融资结构的差异，因此使用M2并不如使用基础货币更具意义。另外郭莹莹(2014)认为伴随着中国金融规模的发展，货币的资本功能逐渐凸显，从而导致无法确定货币供给对汇率的影响方向，这最终取决于货币的一般功能和资本功能的强弱对比，当资本功能小于一般功能时，汇率随着货币供给的增加而贬值，反之，汇率随着货币供给的增加而升值；贸易开放度对人民币实际汇率的影响整体上是负向的，不过也可以看出近些年贸易开放度的负向影响程度逐渐减弱，并在最近一段时间逆转为正。考虑我们用来度量贸易开放度的指标是进出口贸易总和对GDP的比值，近些年中国贸易顺差不断增大，因此在衡量贸易开放度的代理变量中，出口因素起到的作用逐渐占据上风，最终致使贸易开放度增加对人民币有升值倾向的影响；政府财政支出对人民币实际汇率总体上是正向的影响，不过在少数时间也存在负向的关系，逄淑梅等(2015)认为，当政府支出的需求弹性大于税收的需求弹性时，政府支出的增加将导致本币升值，而政府支出的需求弹性小于税收的需求弹性时，政府支出的增加反而会导致本币贬值。因此可以看出中国在绝大部分时间，政府支出对需求的正向弹性是要大于税收的负向作用的。

除此之外，从纵轴方向的概率密度函数曲线还可以判断出，各时变系数正负的分布基本与原均值系数方程的一致。

表4分别是传统BEER模型和半参数变系数BEER模型估计出的人民币实际汇率预测值的均方根误差(Root Mean Squared Error，RMSE)，从表4中可以很明显地看出，半参数变系数BEER模型对实际汇率的预测有了较大幅度的改进。

表4 不同模型汇率预测值的RMSE对比

3.半参数变系数部分线性形式的误差修正模型

在前文中，已建立了传统的向量误差修正模型，误差修正项ECM的系数为-0.018144，表明人民币汇率存在负反馈的自我修正机制。但是基于中国市场经济结构和国际宏观环境不断变化的事实，人民币汇率这种自我调节的能力并不是一成不变的。因此考虑，在误差修正模型中引入半参数部分线性理论，更深入动态地考察人民币汇率的自我调节机制。

半参数变系数部分线性模型可以看成是上文中所使用的变系数模型的推广形式，在它的回归方程中仅把部分解释变量的系数设定为非参数时变的，保留了一些参数系数，本文中所构建的部分线性误差修正模型如下式(11)所示：

D(LNREER)=β0(t)ECM+β1D(LNREER(-1))+β2D(LNFORE(-1))+β3D(LNTNT(-1))+β4D(LNM2(-1))+β5D(LNOPEN(-1))+β6D(LNGOV(-1))

(11)

对于半参数变系数部分线性模型估计方法的研究已有很多，像Li等(2002)、Zhang等(2002)、Fan和Huang(2005)及Zhou和You(2004)等等。本文采用常见的三次均匀B样条估计方法来完成对上式的估计。考虑到主要关心的是误差修正项系数的变化趋势，并且限于篇幅，这里不再给出其他滞后变量所估计的系数。图2是误差修正项系数的走势图。

从图2可以看出，人民币汇率自我调节能力并不是一成不变的，呈现出周期性振荡起伏的态势。总体上绝大部分时间，误差修正项的系数都是负的，即表现为负反馈机制。进一步可以发现两个波峰的时间，一个是在2006年左右，一个是在2015年左右。有意思的是，这两个波峰恰好对应着两次重大的汇率改革：2005年7月21日人民币汇改和2015年8月11日人民币汇改。半参数形式的误差修正模型似乎捕捉到了人民币两次重大的汇率制度改革，根据波峰的时间点，和波峰之后到达谷底的走势，可以明确地看出，人民币汇率的自我修正调节能力是不断变化的，而且受到复杂多变的经济因素和国际因素的影响，在到达谷底后，人民币汇率自身的调节能力进而会逐渐变弱，不过政府审慎择时的汇率改革，能够增强这种能力，但是这种增强具有时效性，根据上图可以发现，在汇改的4至5年后，人民币汇率的自我调节能力会开始逐渐走弱，因此需要政府部门准确把握好汇率走势和经济态势，在恰当的时候施予人民币有效的适应性干预，以维持人民币汇率较高的自我调节弹性。

通过上面的分析，一方面可以看出，任由放任汇率自我调节将会产生不好的影响，这种调节能力会逐渐减弱，最终会由负反馈机制转向正反馈机制，而正反馈机制将会使偏离均衡水平的汇率走向更加偏离的轨道；另一方面也可以发现，中国不断深化的汇率改革和政府有关部门的审慎干预，确实起到了良好的效果，不仅维持了人民币汇率的自我修复能力，而且为人民币汇率弹性不断增强、呈现出双向小幅度波动的态势奠定了良好的基础。

4.人民币实际汇率错位程度测算

使用H-P滤波法提取各个宏观经济因素的长期趋势，带入到半参数变系数BEER方程中，可以得到人民币均衡汇率。再通过式(4)计算出人民币实际汇率的失调程度。图3给出了所测算的汇率失调程度的变化情况。

从图3可以看出，人民币汇率整体失调程度并不大，最大高估不超过9%，最大低估不超过6%，而且可以非常明显地发现，自2015年8月11日汇改以后，人民币实际汇率向均衡汇率逐渐收敛，最大失调程度无论高估还是低估都维持在4%以内，而且大部分时间不超过3%，人民币汇率呈现出围绕均衡汇率双向波动的新态势，并且人民币双向波动更迭的频率逐渐加快，汇率弹性明显增强。

根据本文测算的结果，在2015年8月11日汇改之前，人民币汇率被低估占据大多数，可以看出，至2006年上季度，人民币汇率呈现出短暂的小幅度高估，这应该和2005年7月21日汇改初期人民币实际汇率的大幅度升值相关，之后是持续到2008年7月的低估，其原因主要是中国经常账户顺差的急剧扩大。随后国际金融危机爆发，中国经济增长速度随之放缓，同时中国出口大幅减少并且出现了一定程度的资本外逃，这些因素抑制了均衡汇率的上升，但是世界物价水平的上涨态势致使人民币实际汇率随之上升，从而导致人民币汇率出现了较大程度的高估，最大达到9%。不过这场高估并未持续很长时间，随着金融危机影响的淡化和中国经济的复苏，在2009年6月转为低估，期间欧洲爆发债务危机，世界上各主要国际货币的币值不断下降，引起人民币实际有效汇率逐步下跌，再次加强了低估程度。后来随着中国经济的高速发展，人民币汇率于2011年10月再次出现小幅高估，然后一直到2014年2月，人民币汇率在此期间受2010年6月19日央行重启汇改的影响，已经初步表现出双向小幅波动的趋势。不过从2014年3月开始，人民币汇率出现了较大程度的低估，最大5.6%，这场低估结束于2014年年底，其原因主要在于一方面国际贸易顺差波动较大，2014年上半年甚至出现了贸易逆差，下半年对外贸易帐户逐渐改善，另一方面金融危机以来，国内的经济增长过于依赖房地产行业，市场对国内金融风险的担忧加大和美国QE3等发达国家非常规货币政策的逐步退出引发部分外资撤离中国市场。2015年年初，由于中国通货膨胀的不断加剧而均衡汇率的升幅低于实际汇率的升幅，人民币汇率再次出现高估，但紧接着2015年8月11日的汇改进一步完善了中国的汇率制度，随着中国贸易顺差的缩小、经济增速的放缓，人民币升值的经济基础逐渐淡化，而贬值预期却不断强化，导致高估程度逐渐缩小，并于2016年6月转为低估，且在2017年期间，美联储多次加息，特朗普被选举为美国总统，美元表现强劲，人民币实际有效汇率大幅下降。不过进入2018年后，随着中国央行加强资管监管，受益于美元指数阶段性走弱、国内经济基本面表现稳健等多重利好因素影响，人民币汇率再次出现小幅度窄区间的高估。随后，受国内因素和国际因素的综合影响，以及中国政府有关部门的适当干预调控，人民币汇率双向波动的态势已基本成熟，小幅度的高估和小幅度的低估互相更迭出现，人民币实际汇率围绕在均衡汇率附近波动，最大错位程度不超过2%，基本上处于合理的均衡水平。

可以看出，使用半参数变系数BEER模型测算出的汇率失衡能够很好地反映中国的经济发展状况，与现实相互印证，这表明所建立的模型具有较高的可信度。

四、 央行干预促进作用的检验——基于ESTAR方法

基于前文通过半参数变系数BEER模型测算出的人民币汇率失调，本文将进一步深入探究人民币汇率失调的动态转换特征。鉴于中国所采用的是“有管理的浮动汇率制度”，我们不禁会思考近些年来央行干预在人民币汇率失调和均衡的两区制转换上起着什么样的作用，以及人民币汇率的低估态、高估态和均衡态随着政府介入影响强度的不断改变呈现出怎样的动态演化机制。本节首先回答前面的问题，借鉴陈华(2013)的思路检验和评价近些年来央行干预是否保持了先前推动人民币汇率向均衡水平回复的作用，后一个问题放在下节进行研究。

依据Fiess和Shankar(2009)中对央行干预指数的定义，其测算公式如下：

(12)

其中ΔRt和ΔEt分别是外汇储备变动额和汇率变动额，σΔRt和σΔEt依次为外汇储备变动额和汇率变动额的标准差。当ΔEt等于0时，央行干预指数INTt等于1，此时属于维持固定汇率制度，央行干预最强。本文中为了更直观地体现央行干预指数，将INTt减1，即

(13)

当INTt等于0的时候，央行干预最强，偏离0时，央行干预较弱。

本文选取直接标价法下的人民币兑美元的月度期末汇率计算央行干预指数，图4给出了央行干预指数在样本区间2006年1月-2020年12月的变化情况。从图中可以发现，2008年金融危机发生之前，央行干预强度较小，这段时期正值中国加入WTO后对外贸易经济高速发展的时期，并且在2005年7月21日人民币汇率形成机制改革，人民币汇率不再钉住单一美元，开始实行“以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度”，而金融危机发生之后，央行干预强度最大，央行干预指数基本维持在0的附近，为防范化解经济运行中的风险隐患，中央迅速把宏观调控的首要任务从“防止经济增长由偏快转为过热、防止价格由结构性上涨演变为明显通货膨胀”调整为“保持经济平稳较快发展、控制物价过快上涨”，提出要实施积极的财政政策和适度宽松的货币政策。2010年6月19日汇改重启之后，央行干预强度相对之前表现出减弱的趋势，尤其在2015年8月11日的汇率机制改革之后，央行干预强度进一步减弱，这主要在于汇率改革的主要目的是进一步推进汇率的市场化形成机制。

央行干预对汇率失调的U型效应是指央行干预强度过大，也就是当INTt过于接近0时，会延缓或阻碍汇率均衡。考虑到指数型平滑转移自回归模型(ESTAR)拥有U型特征的指数型转移函数，因此可采用ESTAR模型进行实证检验，本文所建立的ESTAR模型如下：

(14)

G(INTt-d,γ,c)=1-exp(-γ(INTt-d-c)2)

(15)

其中，mist是测算出的人民币实际汇率失调程度，p是自回归的滞后阶数，可依据AIC准则进行选择，αi和βi(i=1,2,…,p)为各滞后项的系数，εt是独立同分布的误差序列，G(INTt-d,γ,c)是转移函数，本文中使用的是指数型转移函数，如上式所示。INTt-d是转移变量，d为转移位置，γ为平滑参数，表示一个区制到另一个区制的转换速度或者调整的平滑性，c是位置参数，表示不同状态下的门限值。

依据AIC准则，自回归的滞后阶数p取5，转移位置d取为1。然后对转移函数在c=0处进行泰勒展开并进行非线性检验，检验结果表明人民币实际汇率错位程度具有非线性变化的性质，且存在着两个区制，在两个区制间的状态转移特征可以通过央行干预指数决定的转移函数来捕捉和描述。采用Eviews可以得到ESTAR模型的估计结果如表5所示。

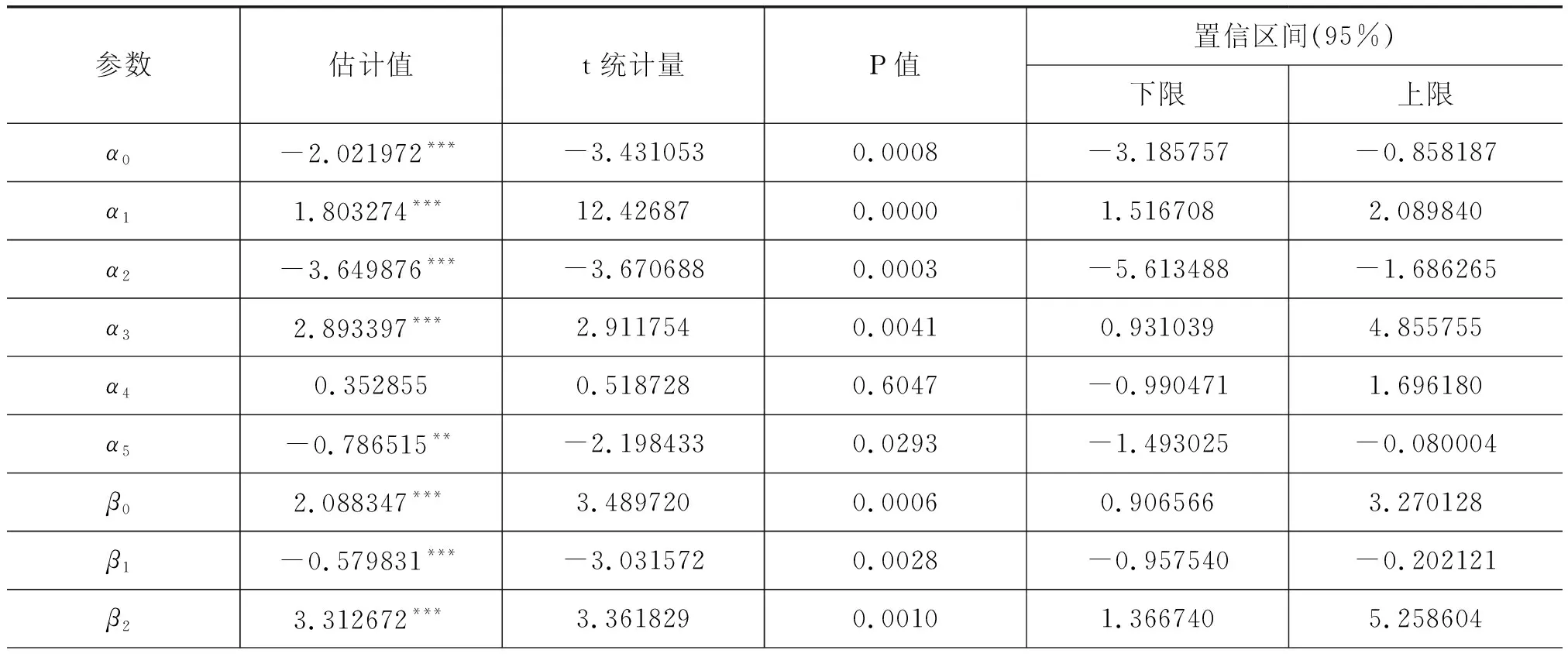
表5 ESTAR模型参数估计结果

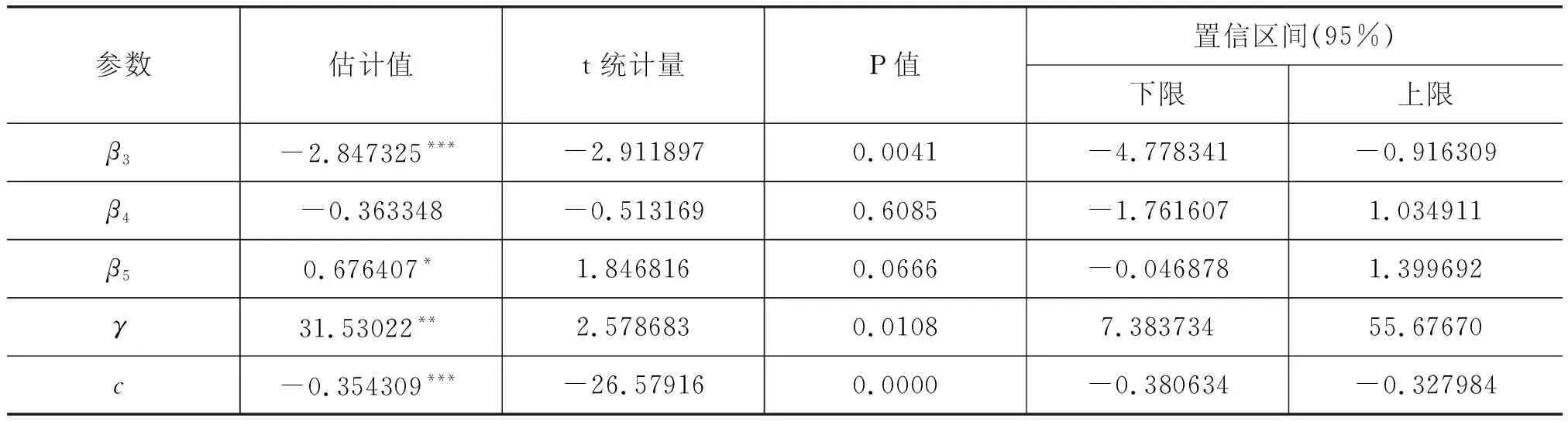
续表

根据表5，人民币汇率错位程度的演变过程可以表示为：

(16)

AR=-2.021972+1.803274mist-1-3.649876mist-2+2.893397mist-3+0.352855mist-4-0.786515mist-5

(17)

(18)

G(INTt-d,γ,c)=1-exp(-31.53022(INTt-1+0.354309)2)

(19)

然后，对模型的残差序列进行自相关和ARCH效应检验，如表6，表中的Box-Ljung Q统计量和ARCH-LM统计量表明残差序列不存在自相关和ARCH效应，验证了所估计模型的合理性。

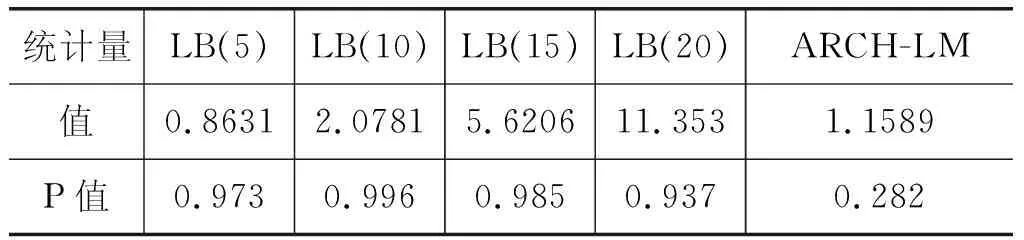
表6 残差检验

由上各式(16-19)，可以进一步推出人民币实际汇率失调的两个不同的区制：

区制0：

mist=-2.021972+1.803274mist-1-3.649876mist-2+2.893397mist-3+0.352855mist-4-0.786515mist-5

(20)

区制1：

(21)

图5分别给出了两个区制(Regime 0和Regime 1)的广义脉冲响应函数。很明显可以看出，在区制0，一个单位的正向脉冲在40期内对人民币实际汇率失调程度影响不大，但是40个月后会导致其发散扩大。在区制1，一个单位的正向冲击在前2个月会使得汇率失调程度扩大，即我们在这里发现了汇率失调的 “超调”特征，在此之后汇率失调程度不断减少，总体上衰减期为37个月，这个结果与陈华(2013)的36个月十分相似。据此可以发现，区制0和区制1分别属于人民币汇率的“非均衡”区制和“均衡”区制。

图6和图7分别给出了转移函数值和央行干预指数INTt之间的U型特征关系图以及转移函数值随时间变化的趋势图。人民币汇率在区制0和区制1之间的动态转换是由央行干预指数INTt决定的，图6中横坐标轴和纵坐标轴旁边分别是央行干预指数和转移函数值的箱型图，从图6可以看出，当央行干预指数在0附近时，人民币实际汇率失调程度趋向于区制0，即“非均衡”区制，而当央行干预指数偏离0时，人民币实际汇率失调程度趋向于区制1，即“均衡”区制。从图7可以看出，在样本区间绝大部分时间，转移函数值都等于1，即人民币实际有效汇率都处在“均衡”区制，只有在少数的时间点位于“非均衡”区制。同时，进一步观察近些年来的转移函数值表现，可以看出2017年以后也基本维持前面的结论，人民币实际汇率失调程度在绝大部分时间都是位于“均衡”区制的。以上均表明在2006年1月后的绝大部分时间，央行干预都推动了人民币更加均衡，也就是说，央行干预在绝大部分时间都促进了人民币汇率回归经济基本面。

总的来说，在不断变化的国际经济环境和国内经济结构转型升级的大背景下，人民币汇率稳定健康的走势得益于中国政府对汇率的适当调控：其一，审慎择时的汇率机制改革，能够显著地增强人民币汇率的自我调整能力，使人民币汇率拥有更强的弹性；其二，央行干预在绝大部分时间内都推动了人民币汇率向均衡水平收敛，促使人民币汇率体现出经济基本面的本质特征。

五、 汇率失衡的动态演变机制——基于NHMM-AR方法

1.非齐次隐马尔科夫自回归模型

通过前文分析，发现央行干预在人民币汇率“均衡”区制和“非均衡”区制的路径转移上起着至关重要的作用，接下来本文将基于非齐次隐马尔科夫自回归模型(Nonhomogeneous Hidden Markov Autoregressive Model, NHMM-AR)从一个全新的视角进一步探讨，在央行干预的影响下人民币汇率失衡内部的动态演变机制。

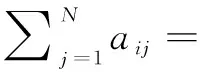
需要注意的是，标准的HMM有两个基本设定：其一，各隐状态间满足一阶马尔可夫性且状态转移概率矩阵不变，即齐次性设定；其二，当前的观测值仅仅依赖于当前的隐状态，并由发射概率分布决定，而观测值之间没有关系。

齐次性HMM假设模型的状态转移概率矩阵不受外部经济变量的影响，但在面对经济金融问题时，具体地像本文所讨论的人民币汇率低估、均衡和高估的问题，各个隐藏状态(低估、均衡和高估)之间的转移概率不可避免地会受到外部一些经济因素的影响，但是齐次HMM无法对这种影响作出更加准确细致的刻画，更无法深入细节地描述人民币汇率各状态间的动态演变机制，这就在一定程度上导致了信息的损失。因此为了降低这种信息损失的影响，本文将采用非齐次HMM(Banachewicz等，2008)来研究人民币汇率失调的动态变化。非齐次HMM的状态转移概率依赖于外部输入的协变量，前文我们已经通过ESTAR模型检验了央行干预在人民币汇率失调和汇率均衡之间所起到的关键作用，因此接下来继续采用央行干预指数作为影响状态转移概率的外部协变量。具体而言，状态转移概率具有如下的probit函数形式，

aij,t=P(St+1=j|St=i,Zt)=Φ(α′ijZt+βij)

(22)

其中Φ(x)为标准正态的累积分布函数，Zt是外部协变量，这里采取央行干预指数INTt，另外为了可识别，需要设定系数矩阵[αij]N×N和[βij]N×N每行元素中的一个为0，例如αii=0和βii=0。

其次，标准HMM假定观测值仅由当前隐状态和发射概率分布来决定，发射概率分布可采取离散分布或连续分布的形式。Hamilton(1989)提出使用ARMA模型来取代发射概率分布，通过ARMA模型对观测序列进行建模，能够更为准确地描述经济时间序列的短期相关关系。HMM-AR模型的观测序列模型定义如下：

(23)

其中，εt是白噪声。表7给出了前文测算的人民币汇率失调的Ljung-Box自相关检验，从表中可以发现各Ljung-Box Q统计量在1%的显著性水平下均拒绝不存在自相关的原假设，说明汇率失调序列存在短期的自相关线性关系，支持了我们使用AR过程来对观测序列进行建模的决定。

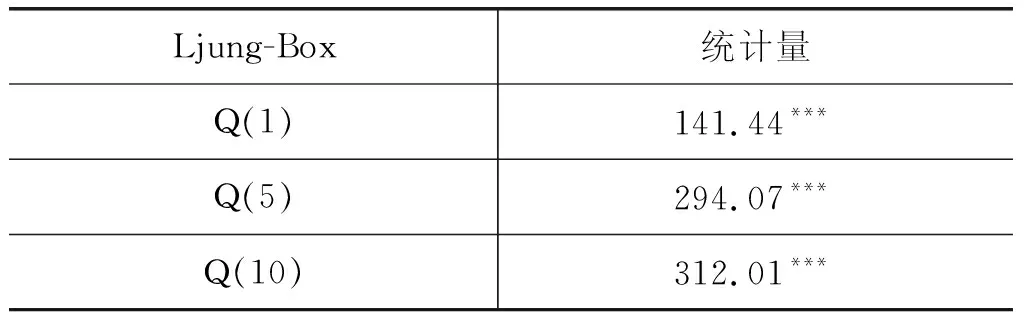
表7 人民币汇率失调的自相关检验

综上所述，本文将采用NHMM-AR模型来探究人民币汇率失调的时变演化机制。

2.人民币汇率失衡的动态演变机制

考虑到汇率所存在的低估、均衡和高估三种状态的经济意义，将NHMM-AR模型的隐藏状态数目设为3，而对于自回归AR模型，鉴于我们的数据量样本较小只有180个，为了避免引入太多待估参数，我们采用AR(1)过程描述NHMM模型的观测序列。考虑到EM算法对初值设置较为敏感，容易陷入局部极值，因此我们反复进行了多次试验，选择了相对较好的估计结果。通过Baum-Welch 算法迭代地求解出NHMM-AR模型的参数后，采用Viterbi 算法解码出人民币汇率失调的隐藏状态序列，图8是NHMM-AR模型训练过程的对数似然值曲线，可以看出模型训练最终达到了较好的收敛状态。图9是人民币汇率失调的全局解码图，图中不同的背景色表示不同的隐藏状态，白色是均衡态，浅灰色是低估态，深灰色是高估态，依次分别记为state1、state2和state3。从图中可以发现，除了少数状态的识别有误以外(比如初期极少数的状态识别结果出现了边缘效应)，整体而言，NHMM-AR模型都较好地推断出了汇率失调的不同隐藏状态。而图10是各隐藏状态在不同时期的平滑概率走势图。

表8是各隐藏状态对应的观测序列自回归过程的所估参数值，据此可以得到各状态下观测序列的脉冲响应图，见图11，由图可知，只有均衡态state1下的脉冲响应图呈现出快速收敛的趋势，而低估态state2和高估态state3的脉冲响应图均在40期左右呈现出发散的趋势。这与上节中“非均衡”区制的脉冲响应函数的表现基本一致。

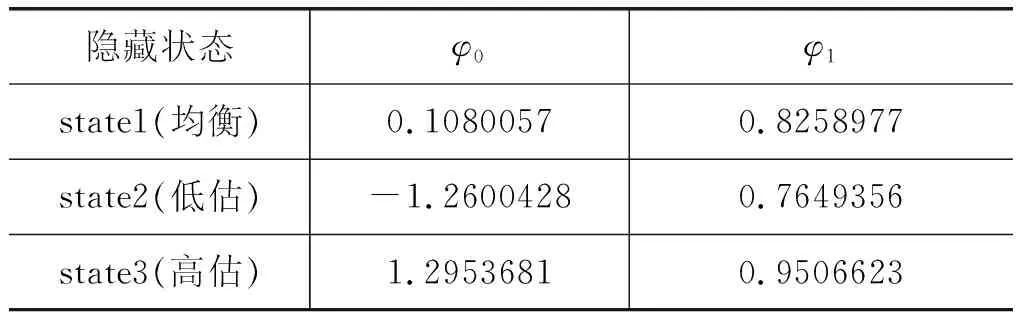
表8 各隐藏状态AR过程所估的参数值

接着考察不同隐藏状态下的各个参考指标，见表9，包括不同状态的均值、标准差、总持续时间(即子样本大小)、发生次数和平均每次持续时间，以及对各状态均值显著性进行检验的z统计量，z统计量定义为:

(24)

其中ui、σi和ni分别是各状态的均值、标准差和总持续时间。

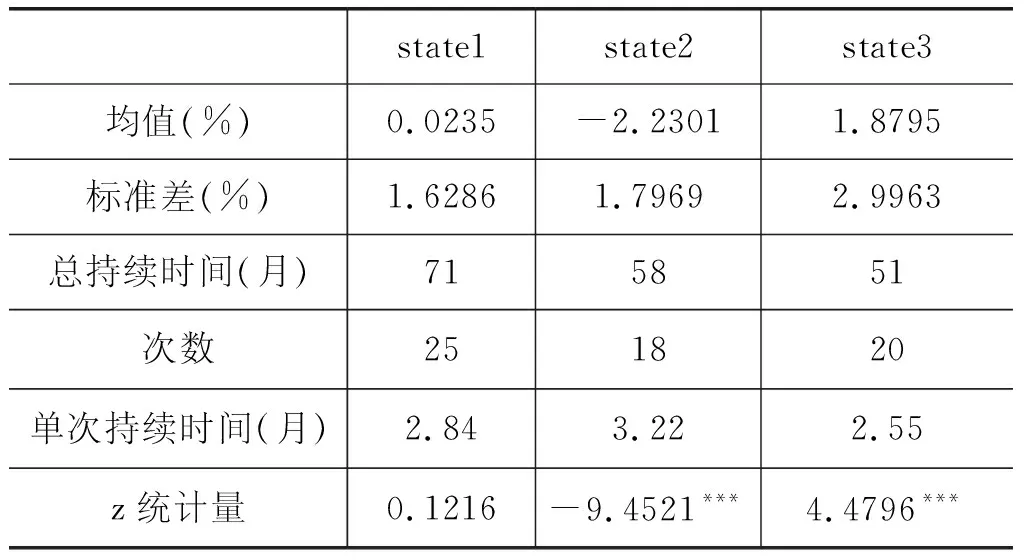
表9 各隐藏状态的参考指标

观察表9能发现，state1的均值只有0.0235%，而且z统计量未通过显著性检验，而state2和state3的均值分别是-2.2301%和1.8795%，而且z统计量均在1%显著性水平下拒绝原假设，进一步佐证了state1、state2和state3分别是均衡态、低估态和高估态，这里需要强调的是，我们将state2和state3分别命名为低估态和高估态，仅仅是出于统计指标大小上的区别，可以看出它们均值的绝对值大小处在2%上下，这充分表明中国汇率基本不存在较大的错位程度，而是围绕在均衡汇率附近双向波动。进一步可以看出，均衡态的标准差最小，这与直觉上对均衡概念的理解比较相符，而低估态和高估态的标准差都要大于均衡态，特别是高估态的标准差将近2倍于均衡态，应该主要与2008年期间人民币汇率出现了较大程度的高估相关。在总持续时间和发生次数两指标上，均衡态都要大于两个失调状态，不过对于单次平均持续时间，低估状态最大，为3.22个月。

最后要重点关注的是央行干预指数作为协变量的时变状态转换概率，其走势图见图12，同时图中给出了12个月的平滑值曲线，以方便进行观察分析，而表10则为时变状态转移概率在时间上的均值。首先观察转移概率的平均值，从表10可以知道，3个状态间持续性最高的是低估态state2，其自转移概率最大为0.6803792，而持续性最低的是高估态，自转移概率仅为0.49703468，不足0.5，这体现出人民币汇率所自有的鲜明特征。另外一个比较有意思的现象是，低估态向高估态转移的概率仅为0.04547024，但是反过来这个概率为0.2689299，即人民币汇率失调存在着显著的不对称性，相对而言低估态的力量要强于高估态。

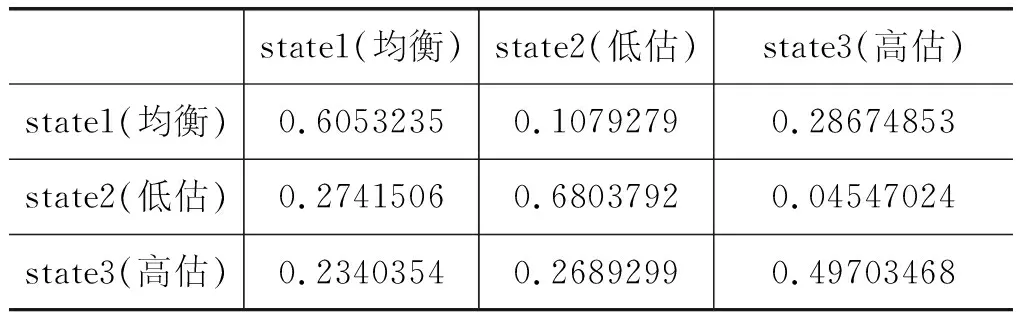
表10 各隐藏状态转移概率的平均值

平均值是从总体上来把握各隐藏状态间的转移关系，但是无法准确描述出转移概率的时变特性。观察图12可以总结出以下三点新的发现：① 近些年来，均衡态的自转移概率(state1->state1)呈现出不断增大的显著趋势，从2009年的0.55 左右增加到2020年的0.7以上，而低估态的自转移概率(state2->state2)和高估态的自转移概率(state3->state3)都不断减少，尤其以高估态最为明显；② 低估态和高估态向均衡态转移的概率(state2、3->state1)都表现出增加的趋势，而均衡态和低估态向高估态转移的概率(state1、2->state3)均显著下降；③ 2008年金融危机期间，均衡态的自转移概率(state1->state1)一度增加达到峰值，这可能与此时期中国政府干预的突然增强相关，从图4的央行干预指数的走势可知，这段时期央行干预程度达到最大，虽然根据前文的测算金融危机期间人民币汇率呈现出较大的高估，但这并不矛盾，为防范化解经济运行中的风险隐患，2008年中央迅速介入并提出要实施积极的财政政策和适度宽松的货币政策，从内在极大提升了人民币汇率的均衡自维持概率。结合①和②的发现，我们可以得出结论，近些年来人民币汇率均衡的持续性不断增大，也侧面折射出人民币汇率回复均衡水平的弹性不断增强，人民币汇率失调的发生概率不断降低。

六、 结 论

本文基于半参数变系数BEER模型对2006年1月到2020年12月的人民币均衡汇率和汇率失调程度进行了测算和详细的分析，并在此基础上，进一步通过ESTAR模型和NHMM-AR模型分别实证研究了央行干预在人民币汇率失调变化过程中起到的关键作用以及人民币汇率失调的动态演化机制。本文得到的主要结论如下。

第一，随着汇率机制改革的不断深化，在不同的经济发展阶段，各基本经济因素对人民币汇率的影响也不断变化，呈现出非线性的特征。相比传统的BEER模型，半参数变系数BEER模型提供了更加丰富的信息。

第二，向量误差修正模型的误差修正项的系数只能反映出人民币汇率的平均自我调节能力，而半参数变系数部分线性模型的引入能打破这种局限性。经过研究发现，人民币汇率的自我调整能力随时间呈现出周期性起伏的趋势，汇率机制的改革能够重新给予人民币汇率自我调整的活力，自我调节能力呈现出达到最大值(谷底)后再逐渐减弱的趋势。

第三，在样本区间内，人民币汇率没有出现较大幅度的失调。最大高估不超过9%，最大低估不超过6%，并且自2015年8月11日汇改以后，人民币汇率呈现出围绕均衡汇率双向波动的新态势，最大失调程度无论高估还是低估都维持在4%以内，而且大部分时间不超过3%，人民币汇率双向波动更迭的频率加快，汇率弹性明显增强，人民币汇率基本上处于合理的均衡水平。

第四，在样本区间的绝大部分时间内，央行干预使得人民币实际汇率基本处于“均衡”区制，央行干预推动人民币汇率向均衡收敛，使之更能展现经济基本面。

第五，人民币汇率失调存在着显著的不对称性，低估态的持续性要显著强于高估态，且高估态转向低估态的概率也显著大于低估态转向高估态的概率。

第六，近些年来人民币汇率均衡态的自维持概率不断增加，人民币汇率向均衡水平收敛的趋势较为明显。

本文的实证研究结果主要给我们以下三条启示：其一，调整对外贸易结构，推动中国进出口结构的转型升级，增强人民币汇率的抗风险能力，降低未来国际金融危机对中国汇率失调的影响程度；其二，审慎择时地进行汇率机制改革，汇率改革应准确把握人民币汇率运行的内在机制，增强人民币汇率的自我调整修复能力；其三，央行适时的干预促使人民币汇率更加均衡，中国政府在不同时间段对央行干预强度的把握比较准确。随着人民币汇率市场化程度的逐渐加深，中国应更为审慎且积极地利用市场干预防止人民币汇率出现较大的波动，使得人民币汇率保持在合理、均衡水平上，维持人民币汇率的均衡。