基于多智能体技术的舰炮备品备件配置方法

董正琼，唐少康，李晨阳，聂磊*，周向东，丁善婷，范宜艳

1 湖北工业大学，机械工程学院，湖北 武汉 430068

2 湖北省现代制造质量工程重点实验室，湖北 武汉 430068

0 引 言

在执行远离基地的海外任务时，舰船装备二级维修保障体系中的部队级是最及时且有效的保障途径。作为部队级维保基础，备品备件为维修活动提供物资，其存储量直接影响到保障任务的成功性[1-4]。但受到空间限制，舰船通常无法溢出式地携带备品备件，故在满足任务成功性的条件下合理地配置各类备品备件，对于提高舰船装备的部队级维修保障能力非常重要。

目前，已有许多学者针对装备备品备件等维修保障资源的优化配置方法开展了大量研究[5-7]。蔡芝明等[8]给出了一套装备备件重要程度的评价指标，利用该关键性参数可优化备件库存；阮旻智等[9]利用边际优化算法对随舰携带的备件数量进行了优化；朱亚红等[10]通过一种变精度粗糙集模型对多资源补给点的最快资源配置路径进行优化，以提高维修保障能力；Sun 等[11]基于贝叶斯方法对飞机故障时间和故障次数进行预测，从而方便订购合适数量的备品备件。Romeijnders 等[12]先对每种部件的修理次数和备件需要数量进行预测，进而对备件总体需求进行预测，最后实现了维修保障资源的优化配置。虽然上述研究通过各种算法对备品备件进行了配置优化及预测，但均存在过度依赖历史数据，无法考虑舰炮装备各个单元部件运行状态之间的相互影响，难以实现备件需求量的准确预测。

为此，本文将结合多智能体建模技术[13-14]，利用Anylogic 软件模拟舰炮装备关键子系统与单元部件的功能与运行状态，结合单元部件的失效率以及备品备件的需求率等信息进行蒙特卡洛重复性仿真试验[15-16]，并考虑资源补给不及时的若干情况。通过模拟舰炮装备的真实保障过程，同时统计与分析备件满足率、备件利用率等指标，实现随舰备品备件携带方案的评估与优化配置，进而提高舰炮装备的维修保障能力。

1 基于多智能体的舰炮装备维修保障模型分析

1.1 舰炮装备结构与保障流程

舰炮装备是一种复杂多层次的嵌套结构，如图1 所示，主要由补扬弹子系统、供弹子系统和发射子系统组成[17]，每个子系统又可细分为若干单元部件，单元部件的运行状态会逐层向上传递。

单元部件的运行过程和保障流程如图2 所示，装备发生故障进入队列后提出保障需求，接着排队等待维修资源保障库进行调配工作。若保障小组能满足故障单元的保障需求，则对设备进行故障检测，在进行换件维修时还需判断保障资源库中的剩余备品备件是否足够，若不足将导致维修失败；当保障小组不能满足保障需求时，需进一步判断等待时长是否超时，超时将导致维修任务失败，若在允许时长范围内，则继续入队等待维修。

图2 维修保障工作流程图Fig. 2 Flowchart of maintenance assurance work

1.2 舰炮装备多智能体的状态行为定义

智能体是一个既能独自思考，又能够与环境进行交互的抽象实体。本文利用多智能体建模技术可较为真实地模拟舰炮装备的运行状态和保障流程。仿真建模时，假设各单元部件的重要度相同，即按照维修请求的时间顺序进行；同种专业的保障人员具备相同的维修能力；未在规定时间内开展维修，会因超时导致维修失败。舰炮装备的维修保障仿真模型可分为子系统智能体、单元部件智能体和维修保障智能体3 种类型。3 种智能体的建立思想分别为：

1） 子系统智能体。子系统有2 种运行状态：正常工作和发生故障。前者对应智能体状态的行为是当前所有关键部件处于正常工作状态，子系统正常工作；后者的智能体状态行为是存在一个或者多个关键部件发生故障，子系统无法正常工作。图3 所示为子系统的可靠性框图示例，由6 个单元部件构成了混联系统。其中，串联的单元部件1～3 或6 发生故障将直接导致子系统故障，并联的单元部件4 和5 必须同时出现故障才会引起子系统故障。因此，子系统的运行状态通过可靠性框图进行判断，其状态转移过程如图4(a)所示。

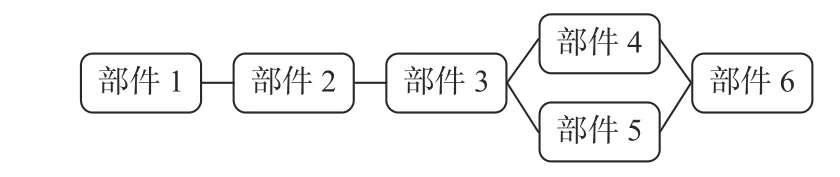
图3 子系统的可靠性框图示例Fig. 3 Example of the reliability block diagram for a subsystem

2） 单元部件智能体。单元部件的运行状态分为以下3 种：正常运行、故障发生和维修状态。对应的智能体状态行为分别为：当前处于正常工作的状态，向子系统智能体发送“运行正常”信息；发生故障，向子系统智能体发送“故障”信息，并进入故障队列，排队等待维修；接收到维修保障智能体对其发出的“开始维修”信息后，开始进行维修工作。图4(b)所示为单元部件的状态转移示意图：发生故障后，单元部件由正常运行转移至故障状态，在保障资源充足的前提下进入维修状态，否则进入排队等待状态，维修完成后返回正常运行状态。

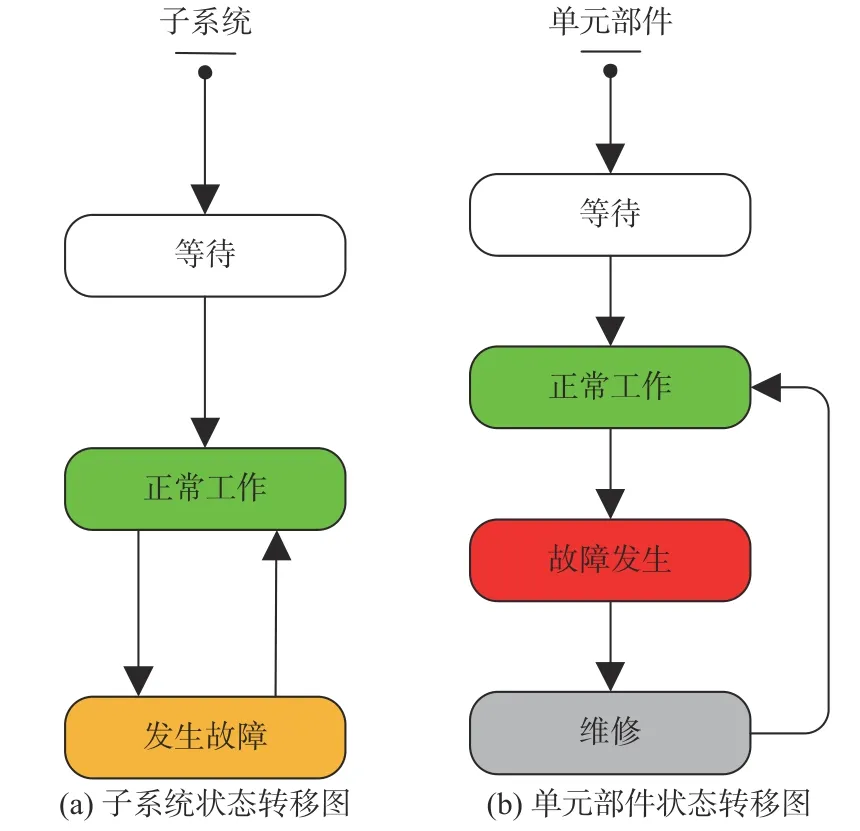
图4 状态转移图Fig. 4 State transfer diagram

3） 维修保障智能体。该智能体分为空闲和工作2 种状态。空闲状态：保障对象无故障发生，不执行保障活动；工作状态：收到装备维修请求后查询自身属性（保障小组与备品备件），判断是否满足故障单元的维修条件，并进行相应的资源调度。维修保障智能体的工作流程如图5 所示。

图5 维修保障智能体工作流程图Fig. 5 Workflow diagram of the maintenance assurance agent

2 舰炮装备备品备件配置分析

考虑到每发炮弹的发射时间很短暂，本文采用平均故障间隔发数(mean rounds between failure，MRBF)对其使用寿命进行描述[17]。在每次任务中，将平均故障间隔时间(mean time between failure，MTBF)的任务时间T与MRBF 的炮弹发射总次数N进行转换，并将转换系数 ξ的表达式定义为

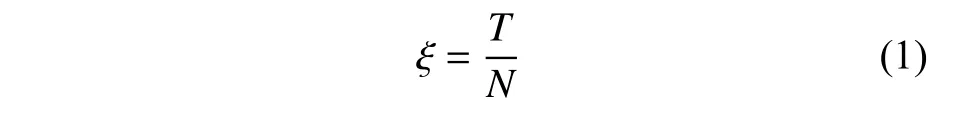
进一步，利用ξ 对装备失效率λR进行等效换算，如式(2)所示：

式中：λR为以发数为单位的失效率；λT为以时间为单位的失效率。

设舰炮装备各单元部件的使用寿命服从威布尔分布，其可靠度函数R(r)为

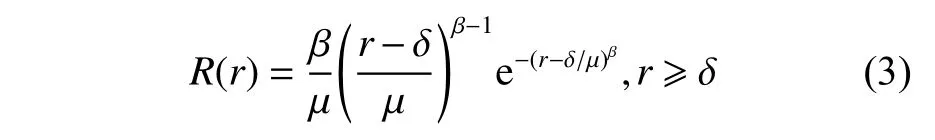
式中：r为炮弹发数；β 为形状参数；μ为尺度参数；δ 为位置参数。单元部件的累计失效率函数F(r)可表示为

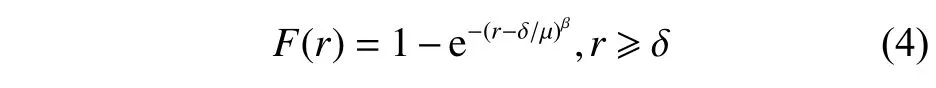
设单元部件的累计失效率为u，0≤u＜1，通过对u=F(r)求取反函数得：

式中，γ 为单元部件的使用寿命。

假设单元部件故障分为2 种类型，即需要和不需要换件修理，对应备品备件的需求量服从泊松分布[18]：

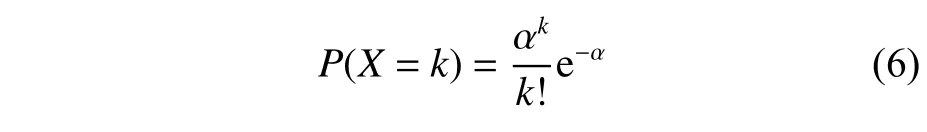
式中：k取值的范围为自然数集；α 为在一个任务时间T内需要进行换件修理故障发生的平均次数，其计算方法为：

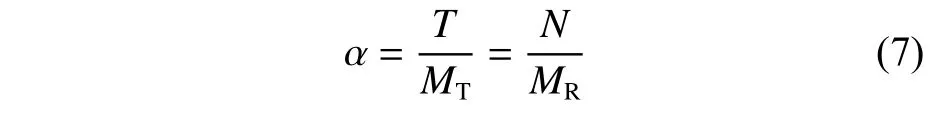
式中：MT为MTBF；MR为MRBF。

对于已知的累积失效率F(r)，利用式(5)和式(6)分别得到的使用寿命γ 和备件需求量X，即可进一步获取需要进行换件修理故障的发生概率p。

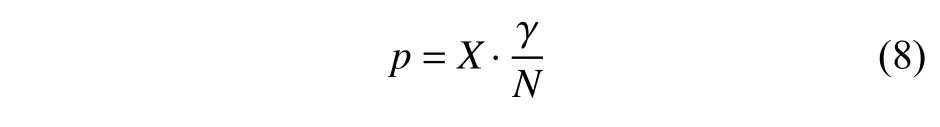
如图6 所示，根据各个单元部件的不同γ 与p，结合多智能体模型模拟装备的运行与保障过程，通过多次蒙特卡洛仿真统计备品备件的使用情况，得到备件满足率、备件利用率等评估指标以及备件需求量的累积分布函数，再根据规定的满足率要求对各个备品备件的携带数量进行更新，进而实现备品备件资源的优化配置。图6 中的4 个评估指标以及备件需求量累积分布函数的计算公式分别如式(9)～式(13)所示。

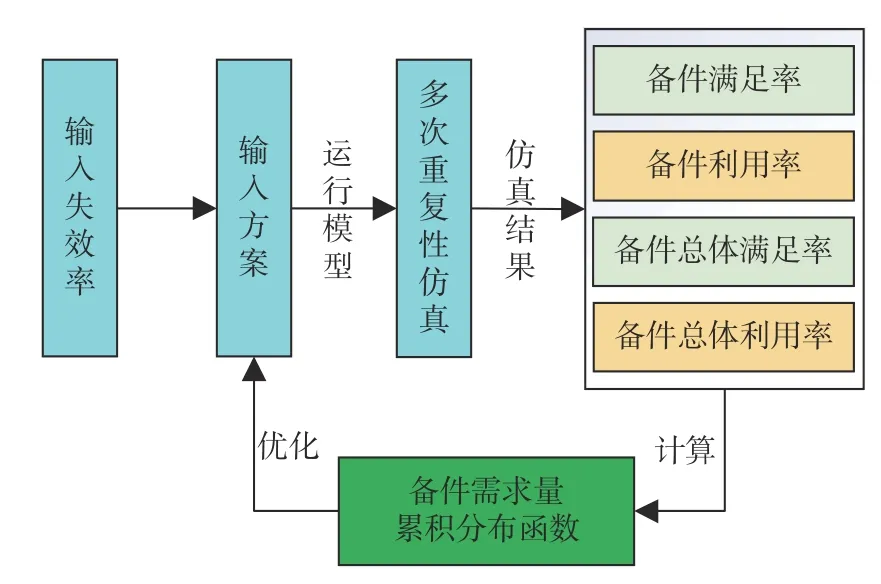
图6 维修保障仿真评估与优化流程Fig. 6 Simulation evaluation and optimization process for maintenance assurance

1） 备件满足率：

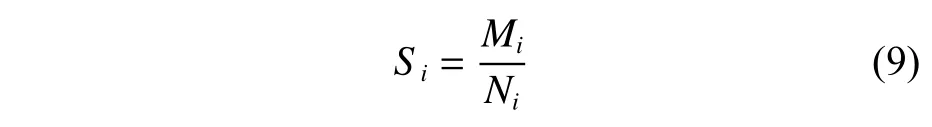
式中：Mi为第i种备品备件完成换件维修的次数；Ni为需求总数。

2） 备件总体满足率：

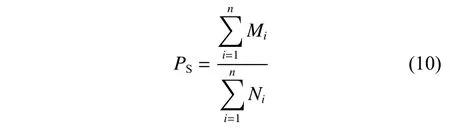
式中，n为备品备件的种类。

3） 备件利用率：

式中：Ui为第i种备品备件的使用数量；Ci为携带数量。

4） 备件总体利用率：

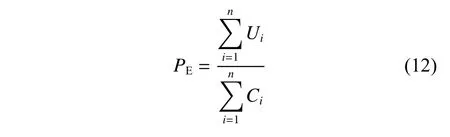
5） 备件需求量累积分布函数：

3 试验案例与结果分析

本文以单100 mm 舰炮为例，针对60 个单元部件进行分析，表1 所示为各单元部件的失效率[17]。

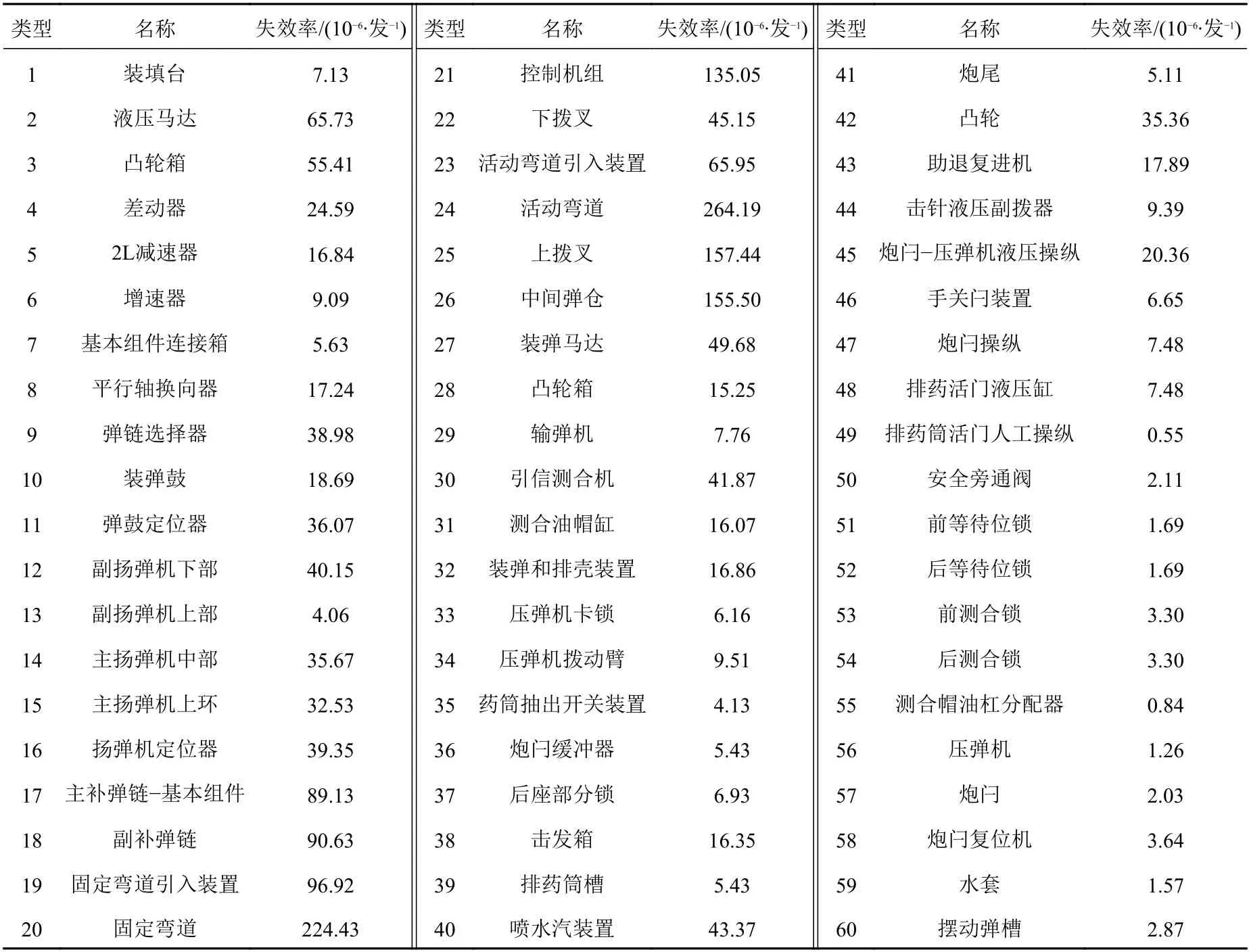
表1 单元部件失效率Table 1 Failure rate of the unit components

首先，通过少量的仿真次数初步统计60 个单元部件的备件需求量。图7 所示为仅15 次仿真模拟试验中，装填台（单元部件1）和液压马达（单元部件2）的备件需求表。若装填台的备件携带数量为0 个，则通过式(9)可计算得到其备件满足率为86%；液压马达的备品备件携带量为2 个时，备件满足率为80%。同样地，以备件满足率达到80%及以上为目的，计算得到其它单元部件的备品备件最少携带数量。表2 所示为根据上述分析结果得出的初始备件配置方案。

图7 舰炮备品备件需求情况Fig. 7 Demand of spare parts for naval guns

进一步地，通过大量仿真试验对备品备件的初始配置方案进行优化，优化目的是在不浪费资源的同时达到理想的备件满足率。进行舰炮维修保障模拟仿真时，将仿真次数设置为10 000 次，在初始备品备件配置方案下，统计备件总体满足率、备件总体利用率以及各类备件满足率等评估指标，并计算出各类备件需求数量的累积分布函数。图8 所示为装填台在10 000 次仿真中的需求情况，其初始方案的携带数量为3。根据式(9)计算得到对应的备件满足率为100%，根据式(13)计算得到在满足率达到90%的前提下，推荐的携带数量为1 个。类似地，以备件满足率达到90%及以上为目的，对其它59 类备品备件的需求量进行分析，优化后的备品备件配置方案如表3 所示。

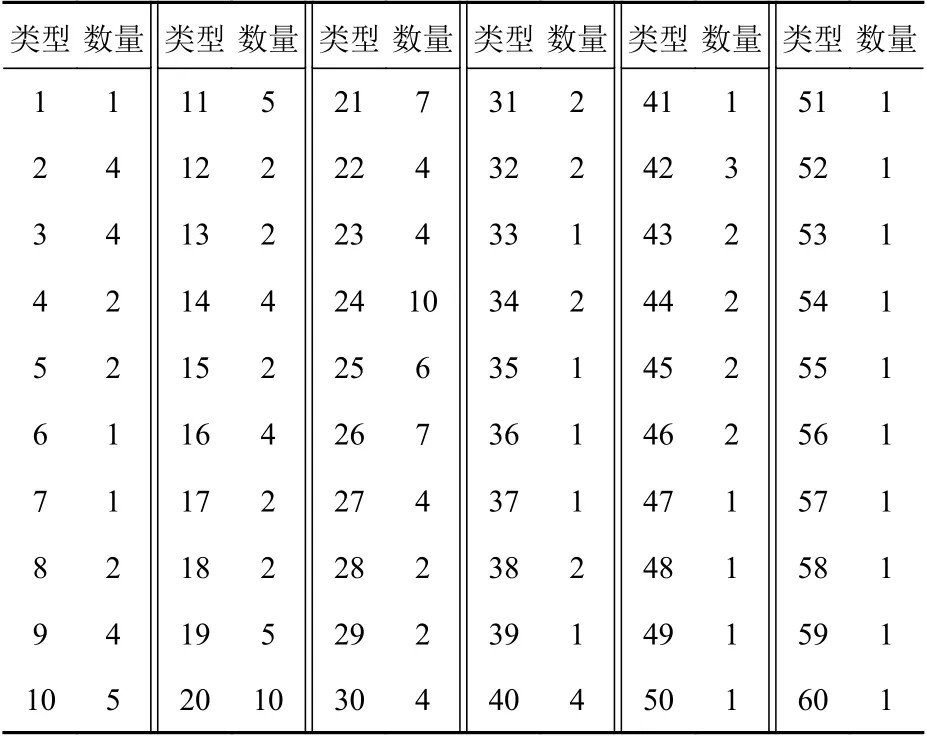
表3 优化的配置方案（数量：个）Table 3 Optimized configuration scheme

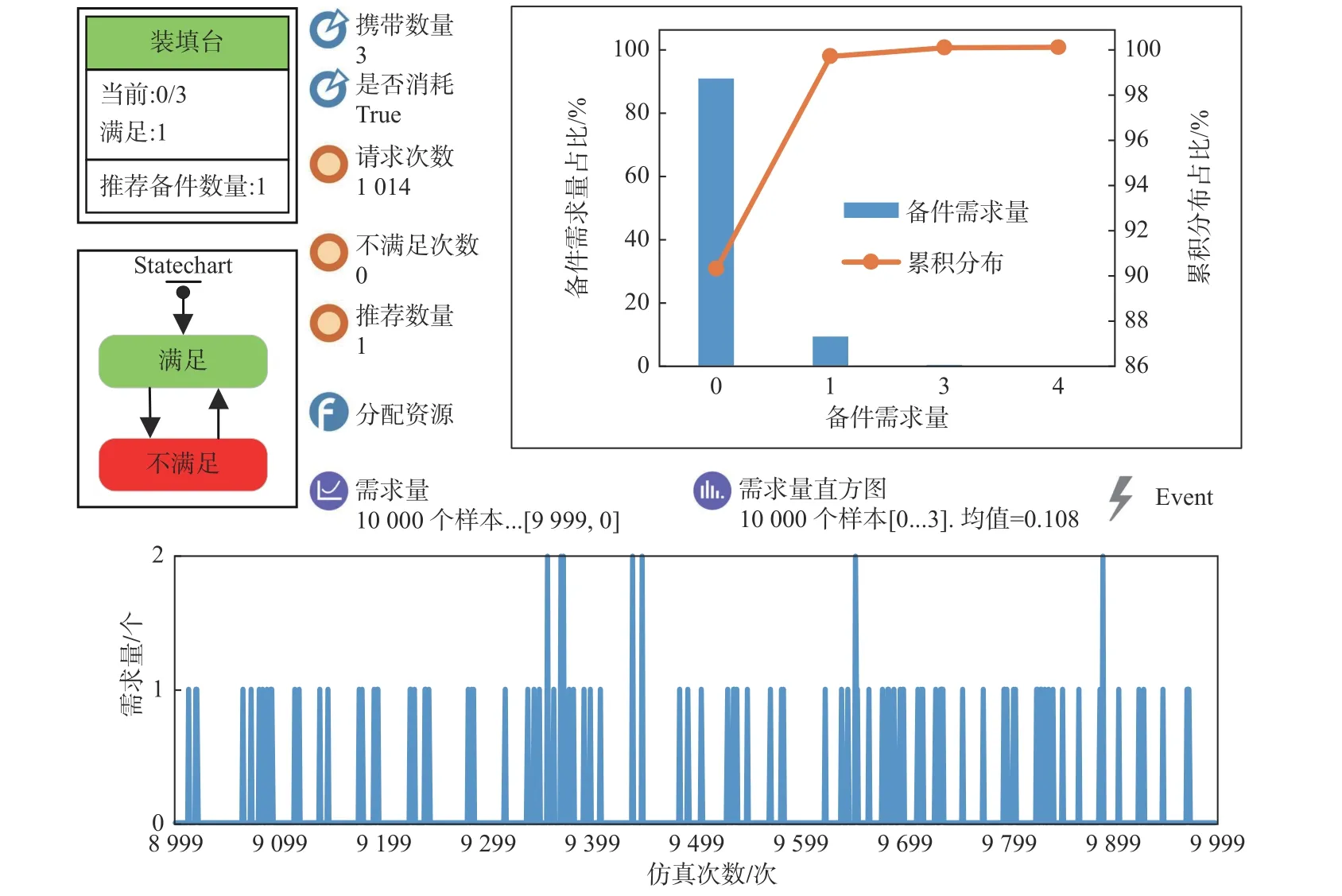
图8 装填台备件需求情况Fig. 8 Spare parts requirements for the loading platform

为证明本文所提方法的有效性，将初始方案和优化方案分别与表4 中的一、二、三等7 类基础式备品备件配置方案进行对比试验。仿真结果表明，备件总体满足率随基础式方案携带备品备件数量的增加而逐步上升，但备件总体利用率显著下降，难以实现资源最大利用与保障能力之间的最佳平衡；与之相比，初始方案在不浪费资源的同时，备件满足率高达94.9%；在初始方案的基础上，优化方案则进一步提高了备件满足率，与基础式方案六相比，其备品备件携带数量下降了约63%，备件利用率提高到基础式方案六的2.5 倍，且备件满足率几乎保持一致。

表4 不同备品备件配置方案仿真结果Table 4 Simulation results of different spare parts configuration schemes

4 结 语

针对舰船装备在执行任务时，备品备件不能及时得到补给，以及存储空间有限等问题，本文提出了一种基于多智能体技术的备品备件配置方法，可同时分析与评估备品备件在不同携带量下的满足率和利用率等指标，进而实现随舰备品备件的优化配置。以单100 mm 舰炮为例，分别建立了子系统、单元部件和维修保障智能体，并定义了三者之间的内部运行逻辑；根据给定的单元部件失效率，模拟其执行部队级保障的工作过程，统计分析获得了备件满足率和备件利用率等指标，进而得到了优化的备品备件配置方案。在备件满足率与基础式方案相近时，备品备件携带数量大幅降低。在后续工作中，将进一步扩大研究范围，增加考虑随舰维修工具的配置对保障能力的影响，并结合机器学习算法对舰炮装备维修保障资源配置进行优化。