基于双偶极向量场的欠驱动无人船目标跟踪制导方法

初庆栋，尹羿博，龚小旋，刘陆，王丹，彭周华

大连海事大学 船舶电气工程学院，辽宁 大连 116026

0 引 言

近20 年以来，海洋航行器已广泛应用于水文监测、生物检测、航道疏通以及搜索和救援等领域[1-4]，其制导和控制已经成为研究的热点问题。根据控制目标的不同，对单一无人船（USV）的运动控制可以分为3 类主要问题[5-6]：目标跟踪、轨迹跟踪和路径跟踪。其中，目标跟踪技术是提高其自主性面临的挑战之一。文献[7]提出了一种直线目标跟踪控制方法；文献[8]针对目标跟踪问题，结合李雅普诺夫稳定性理论和反步法使USV 跟踪到了目标点；文献[9-10]结合A 星路径规划方法，为USV 提供到达目标点的最优路径，实现了目标跟踪；文献[11]基于视觉检测，获得了USV 与目标间的方向及距离，进而跟踪到目标点。然而，传统的USV 目标跟踪技术也存在不足，原因在于：其一，现有技术是根据角度误差来调节制导角速度的，若初始的角速度误差较大，制导角速度会产生较大的暂态振荡和超调，从而影响系统暂态性能[12-13]，导致USV 的跟踪轨迹不够光滑；其二，现有制导方法在跟踪到目标点时会出现奇异点，即稳态时航向不能指定[14-15]。

鉴于上述不足，本文拟提出一种基于双偶极向量场的USV 目标跟踪制导方法。根据双偶极向量场原理，设计一种欠驱动USV 的前向速度和艏摇角速度的导引律。然后，通过稳定性分析，以证明控制系统的有界稳定性。最后，通过仿真与实验验证所设计的目标跟踪制导方法的有效性。

1 问题描述

1.1 欠驱动无人船

本文的研究对象为一种双桨推进的欠驱动USV。USV 的运动方程一般是基于地球坐标系和船体坐标系来表示，如图1 所示。欠驱动USV的运动方程由式（1）[1]描述。

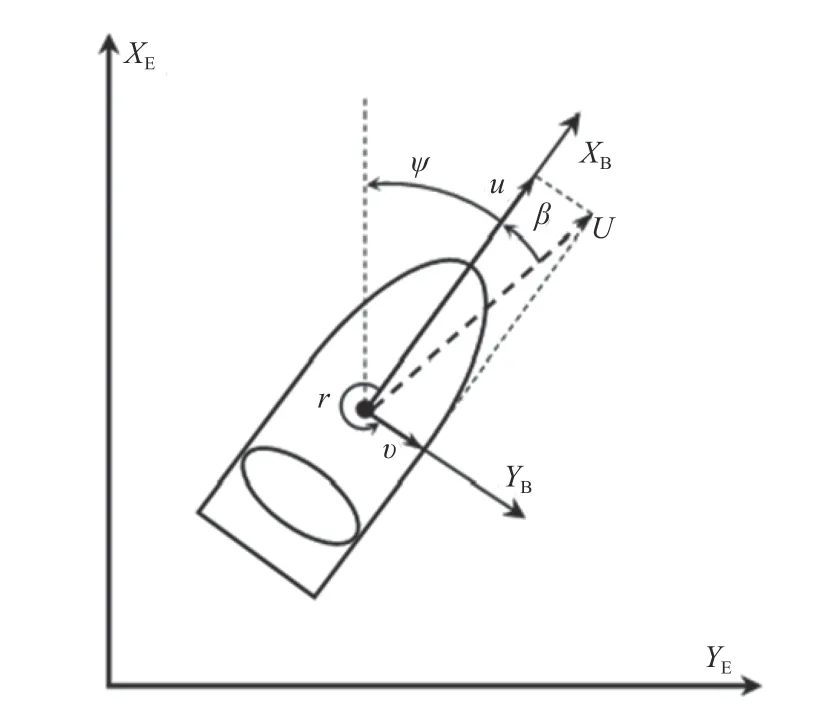
图1 无人船运动的地球坐标系和船体坐标系Fig. 1 Earth-fixed frame and body-fixed frame of AUV motion

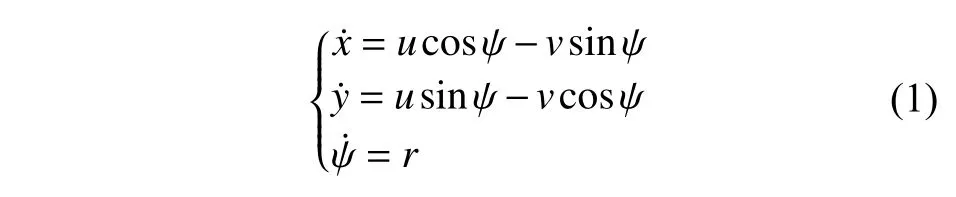
式中： (x,y)表示在地球坐标系（XE-YE）下的位置；ψ ∈(-π,π]， 表示USV 的航向；u,v,r为USV 的速度状态信息，分别表示USV 在船体坐标系（XBYB)中的前向速度、侧向速度、艏摇角速度。

定义USV 的实际运动速度U=(u2+ν2)1/2＞0，实际的运动方向 ψw=ψ+β（ β表示侧滑角），则其运动方程可表示为

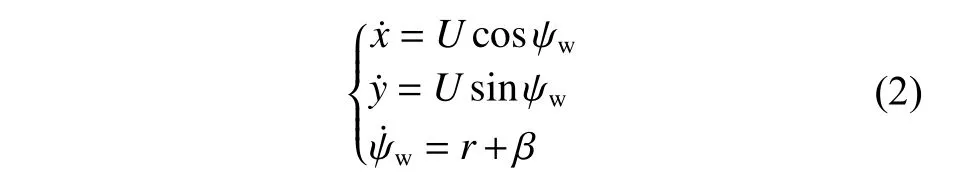
1.2 双偶极向量场

采用双偶极向量场的概念来设计导引律可以使处于向量场中的USV 跟踪到给定的目标点。图2 所示为USV 跟踪给定目标的示意图。F(p*)：R2→R2，采用如下形式表示：

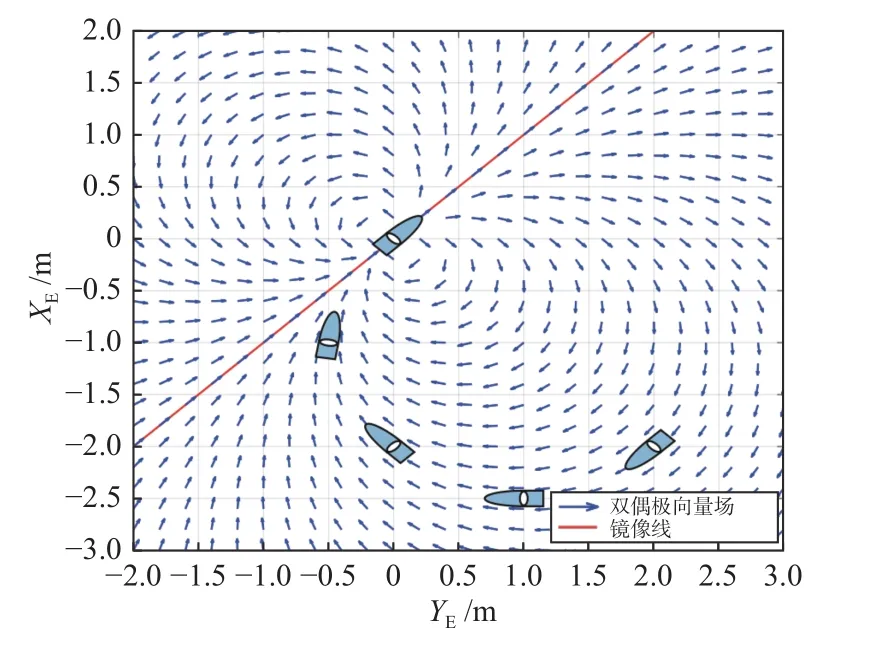
图2 双偶极向量场Fig. 2 Two-dimensional dipolar vector field

双偶极向量场的主要特点是：处于向量场F(p*)内任意一条场线均为一条至目标的路径，内部场线也都是目标点开始至目标点结束。处于双偶极向量场中的USV 都会沿着向量场内部场线到达双偶极向量场的目标点，即沿着光滑的场线跟踪到目标。如图2 所示双偶极向量场，其中，蓝线表示双偶极向量场，红线表示向量场的镜像线，USV 按照向量场的场线跟踪至目标点。

2 导引律的设计和稳定性分析

2.1 导引律设计

为使处于当前位置p的USV 跟踪到目标位置p*，需要设计基于双偶极向量场的导引律。双偶极向量场根据式（3）由下式表示。

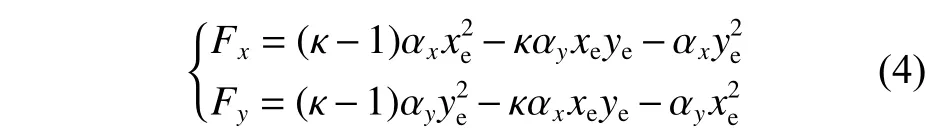
航向误差可表示为

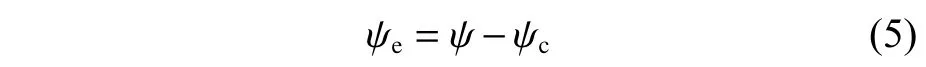
式中：USV 当前位置p的 航向 ψc=atan2(Fy,Fx)，即表示向量场在 (x,y)位置的方向，这里规定ψc=atan2(0,0)=ψ。

基于双偶极向量场的USV 前向速度与艏摇角速度，可设计如下导引律。

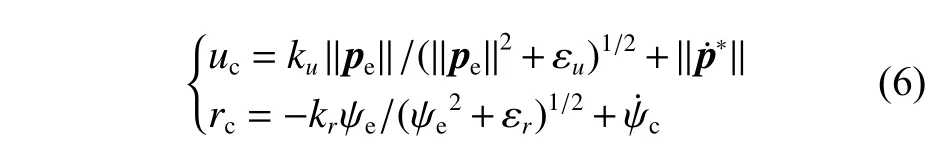
式中：uc，rc分别为前向速度和艏摇角速度的制导信号；ku,kr∈R+，为导引律参数，分别表示前向速度和艏摇角速度的制导增益； ψe为无人船航向与向量场方向间的航向误差； εu,εr为可避免制导信号饱和的参数。

图3 所示为基于双偶极向量场USV 的目标跟踪制导控制框图。

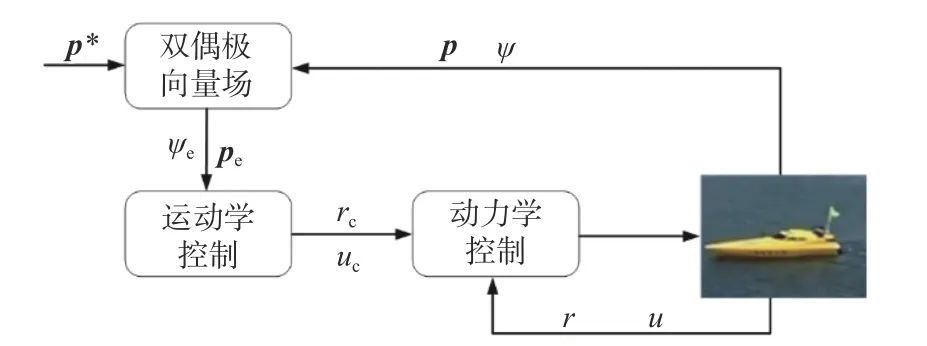
图3 整体控制框图Fig. 3 System structure

2.2 稳定性分析

本节将证明USV 沿着向量场的场线移动并与目标间的跟踪误差最终是一致有界的。

分别对等号两侧进行求导，可得

将航向误差和位置误差代入，可得

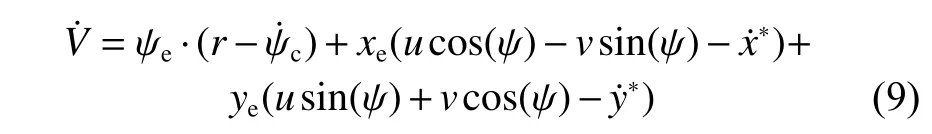
化简后，可得

此时，说明USV 正在接近目标位置参考点，故将其代入式（11），可得

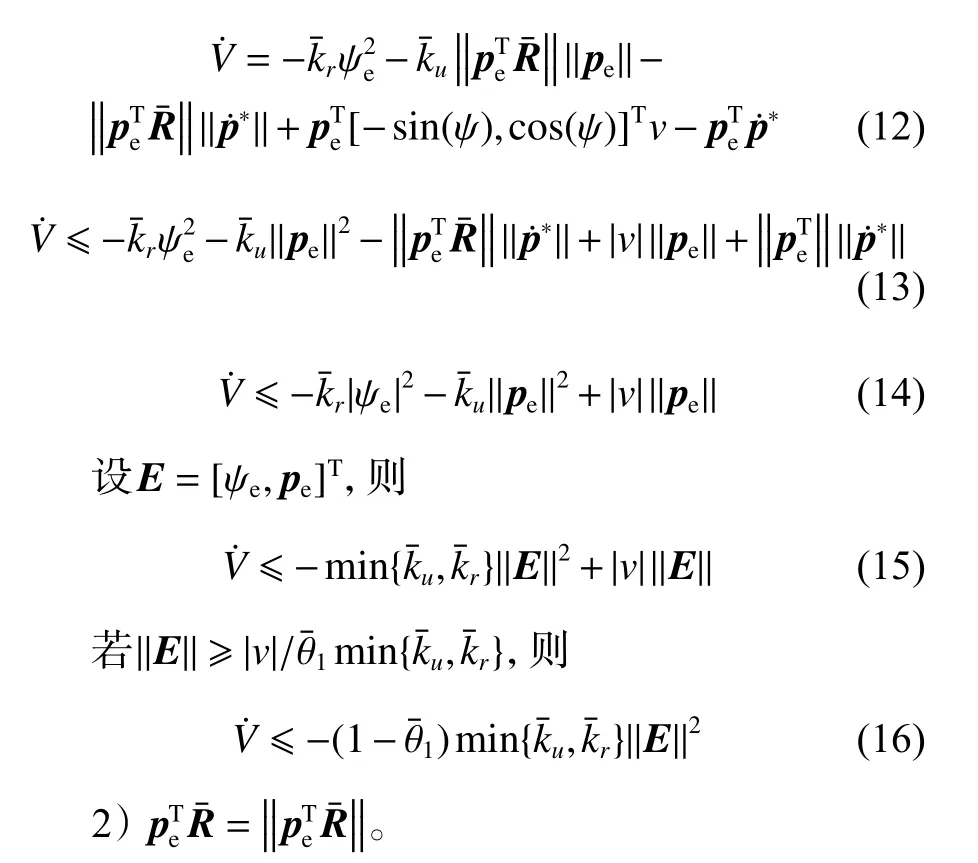
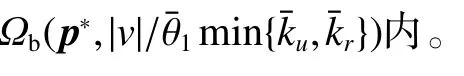
3 仿真结果

本节将给出仿真结果以验证所提方法的有效性。仿真使用Ardupilot 软件在环仿真（SITL+MAVProxy），所用程序即为最终实验程序。Ardupilot 固件本身已很完善，故未对其修改，而是直接作为底层使用，上层则为前文所述基于向量场的制导算法。在ubuntu16.04 系统上进行编译，加入对比仿真试验以验证所提方法的有效性。对比仿真的目标跟踪导引律如式（17）所示。

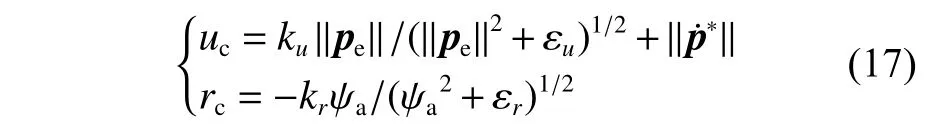
式中： ψa表 示无人船航向与实际方向间的误差，ψa=ψ-ψc，ψc=atan2(pey,pex)，pe=[xe,ye]T=p-p*。

仿真参数的取值说明如下：向量场参数 κ=2；参考点在半径为15 m 的圆形上移动，速度1.2 m/s；导引律参数ku=0.9，kr=1， εu=1 ， εr=1。仿真结果如图4～图7 所示。

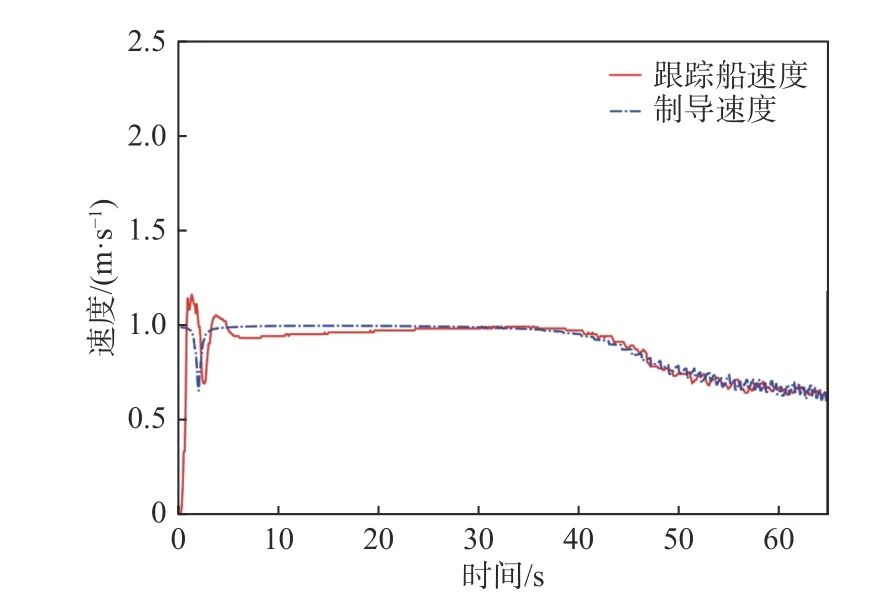
图7 目标跟踪制导时制导速度和跟踪船速度仿真结果Fig. 7 Simulations of velocity of guiding and follower with target tracking guidance

图4 所示为向量场制导和目标跟踪制导时的USV（即跟踪船）轨迹对比。由图可见，经过一段时间后USV 都可以跟踪到给定的目标位置点，但红线轨迹（即有向量场制导时的跟踪轨迹）更光滑，跟踪效果较好。

图4 USV 的仿真轨迹对比Fig. 4 Comparison of simulated trajectories of USV

图5 所示为向量场制导和目标跟踪制导时的USV 艏摇角速度对比。由图可见，在有向量场制导下，2 s 时刻USV 的角速度值达到最大-0.4 rad/s，随后逐渐减小，最终稳定在-0.1 rad/s，此时的USV按照固定的方向旋转，航向不会出现振荡； 在对比实验仿真中，目标跟踪制导时在1 s 时刻USV的角速度达到最大值0.9 rad/s，随后出现振荡，在5 s 时刻达到最小值-0.9 rad/s，在角速度振荡时，USV 的航向也会振荡，对应于图中USV 的轨迹不够光滑。经计算，有向量场制导时的超调量是目标跟踪制导时超调量的30%；

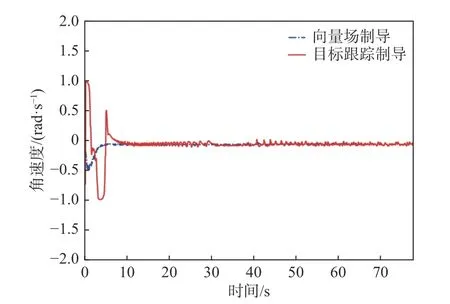
图5 USV 的仿真艏摇角速度对比Fig. 5 Comparison of simulated yaw angular velocity of USV

图6 和图7 分别给出了向量场制导和目标跟踪制导时的USV 速度对比。由图可见，USV 均可以在一段时间后跟踪到制导速度。

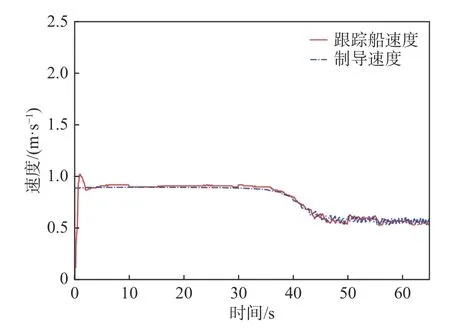
图6 向量场制导时制导速度和跟踪船速度的仿真结果Fig. 6 Simulations of velocity of guiding and follower with vector field guidance

4 实验结果

本文采用实验室的一艘USV 和一台中央监控计算机来验证所提方法的有效性，如图8 所示。USV（即图中跟踪船）的控制器采用的是Raspberry 4B 和Pixhawk，配 有GPS 接 收 器、2 个推进器、2 个电子调速器和WiFi 网桥等通信设备。Pixhawk 内置的姿态传感器可以获得USV 的艏摇角速度和偏航角信息，GPS 传感器可以获取USV 的位置信息和速度信息。2 个推进器用于提供动力。通过网桥组建局域网，与岸基监控系统进行通信，网络的工作频率是2.4 GHz。

图8 目标点跟踪无人船实验配置Fig. 8 Experimental configuration of USV for target point tracking

以下对前文参数在实验中的取值进行说明。由于算法是在软件在环（software-in-the-loop，SITL）中进行仿真，实验参数与仿真参数取值大致相同。向量场参数 κ=2； 导引律参数ku=1.2，kr=1，εu=1 ， εr=1。实验中，虚拟目标点由本地坐标系产生，不在地图上显示。虚拟目标点在半径为10 m的圆形轨迹上运动，速度为1.2 m/s。

图9～图13 所示为根据实验采集的数据绘制成的结果图。

图9 和图10 为目标跟踪制导和向量场制导时的USV 轨迹对比。由两图可见，经过一段时间后USV 都可以跟踪到目标点，但向量场制导的跟踪轨迹没有超调，跟踪效果较好。

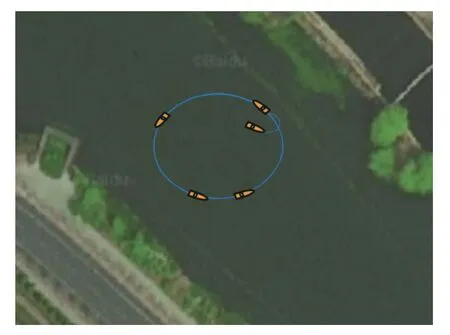
图9 目标跟踪制导时的实验轨迹Fig. 9 Trajectory in experiment with target tracking guidance

图10 向量场制导时的实验轨迹Fig. 10 Trajectory in experiment with vector field guidance

图11 所示为USV 的艏摇角速度对比。由图可见，在有向量场制导时，在3 s 时刻USV 的艏摇角速度值达到最大的-0.7 rad/s，随后开始减小，最终稳定在-0.15 rad/s 附近，且始终小于0，即USV会按照固定方向旋转，航向不会振荡；与实验采用目标跟踪制导时的艏摇角速度进行对比，可见USV 的艏摇角速度波动较大，在4 s 时刻达到最大值-0.96 rad/s，随后开始振荡，当艏摇角速度的符号改变时，USV 的旋转方向也会随之改变，并对应于图9 中的轨迹超调部分。经计算，在有向量场制导时，USV 的艏摇角速度超调量为目标跟踪制导时超调量的58%。

图11 无人船的艏摇角速度Fig. 11 Yaw angular velocities of USV

图12 和图13 所示为向量场制导及目标跟踪制导时的制导速度与USV 跟随速度（跟踪船速度）对比。由两个图可见，USV 的跟随速度均可以跟踪到给定速度，最终给定速度逐渐减小到约1.2 m/s，与目标位置点的速度相近。由于实验所在湖泊存在水草及分布不均匀的情况，在USV 经过水草密集区时，水草会缠绕在推进器上，影响了USV 的航行，这是产生误差的原因之一。总体上，误差是在可接受的控制范围内。

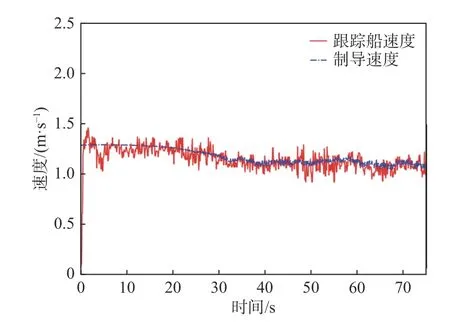
图12 向量场制导时的制导速度和跟踪船速度Fig. 12 Velocities of guiding and follower with vector field guidance

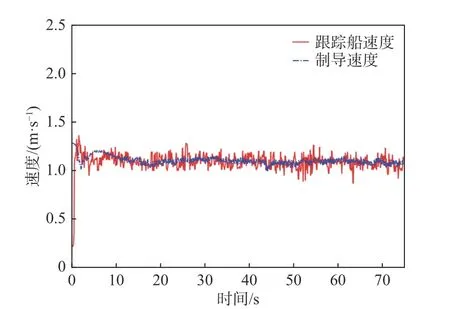
图13 目标跟踪制导时的制导速度和跟踪船速度Fig. 13 Velocities of guiding and follower with target tracking guidance

5 结 语

本文研究了欠驱动USV 的目标跟踪制导问题。首先，根据USV 的运动学模型，设计了一种基于双偶极向量场的艏摇角速度和前向速度导引律； 然后，通过稳定性分析证明了控制系统的有界稳定性； 最后，通过仿真和实验验证了所提设计方法的有效性。结果表明：与传统的目标点跟踪制导方法相比，所提方法因引入了双偶极向量场，USV 可以直接跟踪向量场方向，避免了初始的角度跟踪误差带来的USV 跟踪过程中的振荡和超调，减小了操纵过程中的抖动现象，显著提高了系统的暂态控制性能及航行安全性。同时，在跟踪目标时，能够保持期望的航向，使跟踪目标的轨迹曲线更为光滑，克服了现有方法中稳态航向不能指定的局限性。