欠驱动船舶自适应神经网络有限时间轨迹跟踪

张强，朱雅萍，孟祥飞，张树豪，胡宴才

山东交通学院 航运学院，山东 威海 264200

0 引 言

随着科学技术的发展，对海洋资源开发、运输和勘探的需求日益增加。水面船舶作为一种经济、有效的工具，在海洋工程中起着至关重要的作用。轨迹跟踪控制是船舶运动控制中一种典型的控制任务，它可以使水面船舶跟踪所需要的参考轨迹。随着对水面船舶的使用愈加广泛，轨迹跟踪的控制问题也受到了国内外学者的广泛关注。水面船舶在航行中会受到各种内部和外部的不确定性干扰，在设计轨迹跟踪控制方案时必须考虑上述复杂因素的影响，因此，各种先进的控制方法被应用于轨迹跟踪控制方案设计中。

针对水面船舶轨迹跟踪控制的问题，轨迹线性化控制方法[1]、基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应神经网络控制方法[2]、基于时变非对称障碍Lyapunov 函数的最小参数自适应递归滑模控制方法[3]等被应用于全驱动船舶的轨迹跟踪领域。以上方法解决的是具有不确定条件和未知参数的全驱动船舶的轨迹跟踪问题，并且提高了跟踪精度，但海面上是以欠驱动船舶为主，研究欠驱动船舶对降低成本、提高航运安全具有重要意义。针对欠驱动水面船舶的轨迹跟踪问题，孟威等[4]通过引入滑动平面设计控制律，解决了由模型参数不确定性和未知干扰带来的鲁棒性问题。沈智鹏等[5]提出了动态面自适应输出反馈控制，通过引入观测器，保证了船舶轨迹跟踪误差的最终一致有界性。柳晨光等[6]提出的模型预测控制是将模型近似线性化，但这种方法在外界干扰系数变大时其跟踪误差也会变大。文献[7-8]分别利用观测器和比例积分实现了鲁棒自适应控制，并且文献[8]还实现了进一步减少由滑模控制引发的振动问题。Dai 等[9]通过引入扰动观测器来估计未知干扰，Haseltable 等[10]通过引入神经网络逼近非线性函数，均进一步提高了轨迹跟踪的精度。

然而，以上文献都只有在系统时间趋于无穷大时才能得到一个渐近稳定的结果，没有考虑船舶在各种不确定性影响下能否实现有限时间的跟踪控制。王昱棋等[11]基于终端滑模控制引入分散控制器，提出了一种终端滑模控制方法，可使欠驱动水面船舶在有限的时间内较快地实现跟踪并保持期望的轨迹。Ning 等[12]首先将未知的参数动力学和不确定性封装成非线性函数，再通过自适应模糊逼近器在线识别非线性函数，得到了一种新的直接自适应模糊跟踪控制方法，可实现船舶在有限时间内的跟踪。Sun 等[13]提出了一种事件触发的鲁棒模糊自适应定性能有限时间控制方法。Zhao 等[14]针对具有上界未知干扰的刚性航天器，分别设计了有边界层和无边界层的自适应有限时间控制律，实现了在有限时间内的轨迹跟踪，并能消除抖振问题。

基于以上分析，本文拟设计一种受动态不确定性和未知时变干扰影响下的自适应神经网络有限时间轨迹跟踪控制方案。首先，利用径向基神经网络重构船舶的动态不确定性，并设计自适应律逼近未知扰动的上界。由于径向基神经网络对非线性函数有着高度的拟合关系，因此，提高逼近精度，并在控制方案设计中引入有限时间控制理论，以保证系统跟踪误差能在有限时间内收敛至一个比较小的区域内，提高系统误差的收敛速度。最后，进行仿真对比试验，验证该控制方案的跟踪效果。

1 船舶数学模型与问题描述

考虑如下形式的欠驱动水面船舶数学模型[15]：

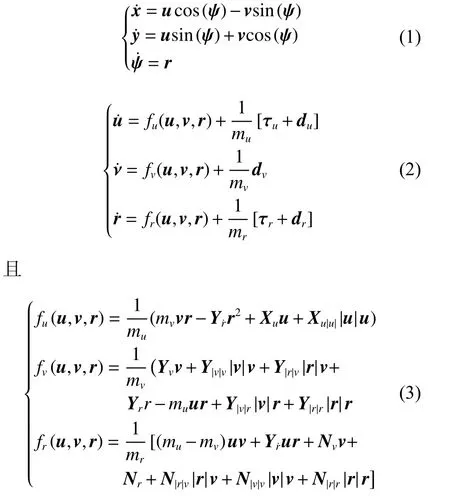
式中：x,y,ψ为水面船舶的实际跟踪轨迹，分别为横向位移、纵向位移、航向角；u,v,r为实际跟踪速度，分别为前向速度、横漂速度和转艏角速度；τu为 船舶纵荡控制力； τr为 艏摇控制力矩；mu，mv，mr为 附加质量；du，dr为 扰动；fu(u,v,r)，fv(u,v,r)，fr(u,v,r)为 未知动 态；Xu，Yv，Yr，Nv，Nr分别为水面船舶在前进、横漂和艏摇3 个维度上的线性阻尼；Xu|u||u|u，Y|v|v|v|v，Y|r|v|r|v，Y|v|r|v|r，N|r|r|r|r，N|r|v|r|v分别为水面船舶在前进、横漂和艏摇3 个维度上的非线性阻尼。

为了实现控制器的设计，现给出如下假设、定义和引理。

定义：非线性控制系统描述如下：

式中：x∈Rn为系统的状态变量； Ω0为包含原点的一个球域；f(x)为一个连续函数，对于任意初始条件x0， 如果存在一个常数 ζ ＞0和一个调节时间函数0 ＜T(0)＜∞，使 得 ‖x(t)‖≤ζ，t≥T(x0)，那么系统可以说是半全局实际有限时间稳定的[16]。其中，t为时间变量，T为初始条件下的时间。

引理1：考虑一个系统x=f(x)，f(0)=0，x∈Rn，其中f(x)为一个连续函数，假设存在一个连续的Lyapunov 函数V：D→R可以使如下条件满足：V是一个正定函数，存在实数ρ1＞0，ρ2＞0，η ∈(0,1)，以及一个原点附近的开环邻域满足V˙(x)+ρ1V(x)+ρ2Vη(x)≤0，则系统是有限时间稳定的，且稳定时间Tr为[17]

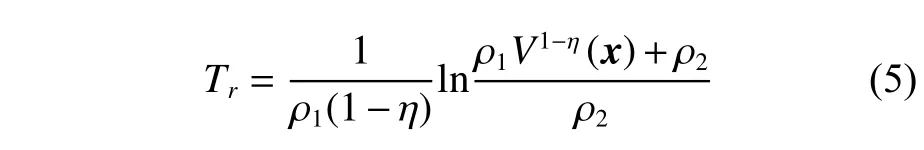
引理2：对于任意给定的定义在紧集 Ω ⊂Rn上的连续光滑函数h(x)[18-19]，有

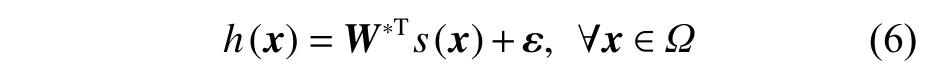
式中： ε为逼近误差，对于所有的x∈Ω，存在向量ε*＞0，且 满足 |ε|≤ε*；W*为理想条件下的权重向量；s（x）为中心函数。通常，理想的神经网络权重为未知向量，需要进行估计。可以理解为x∈Ω ⊂Rn上能使 |ε|最 小化的W，即

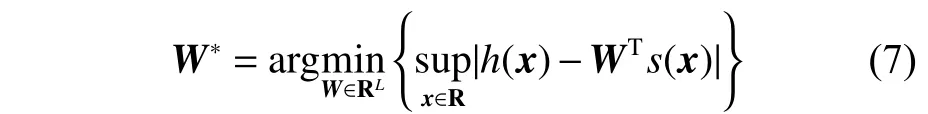
引理3：对任意的a＞0（a为常数）和x∈R，都满足如下的关系[20]：

2 控制器的设计

轨迹跟踪的控制流程如图1 所示。为解决欠驱动问题，采用文献[21]中的方法。首先，定义欠驱动水面船舶的跟踪误差：

图1 轨迹跟踪控制流程图Fig. 1 Trajectory tracking control flow chart

式 中：xl，yl， ψl分 别 为 跟 踪 过 程 中 的 期 望 横 向 位移、期望纵向位移和期望航向角；ul，rl分别为跟踪过程中的期望前向速度和期望转艏角速度。

令

对式(11)求导，可得

式中，k11，k12，k31，k32，δ 为可调参数。

根据式(13)设计期望的前向速度、转艏角速度和航向角：

式 中 ，ψl通 过ul=‖α‖反 解 得 到， αx，αy为 α在x,y方向上的分量。

对式(10)求导，可得

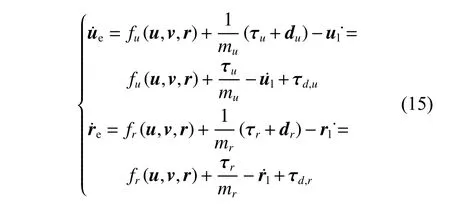
对于未知动态fu(u,v,r)，fr(u,v,r)，利用RBF 神经网络进行重构，即

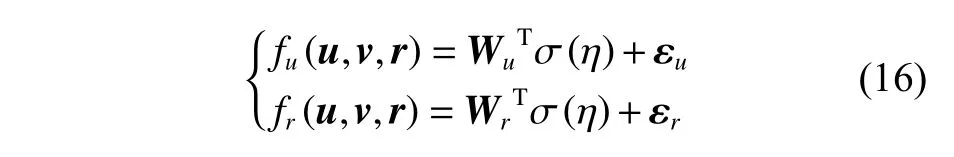
式中：网络输入信号 η=(x,y,ψ,u,v,r)T， σ(η)为神经网络权值自适应律中的中心函数；神经网络权值矩阵分别为Wu=(wu1,wu2,···,wuh)T，Wr=(wr1,wr2,···,wrh)T； εu， εr为神经网络逼近误差。

为稳定ue，re，设计控制律，如式(17)所示。

3 稳定性分析

为了验证欠驱动船舶控制器的稳定性，设计如式(20)所示的Lyapunov 函数。

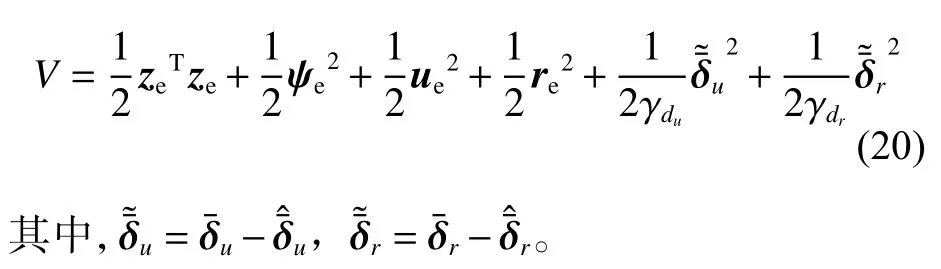
对式(20)求关于时间的导数，可得

其中：

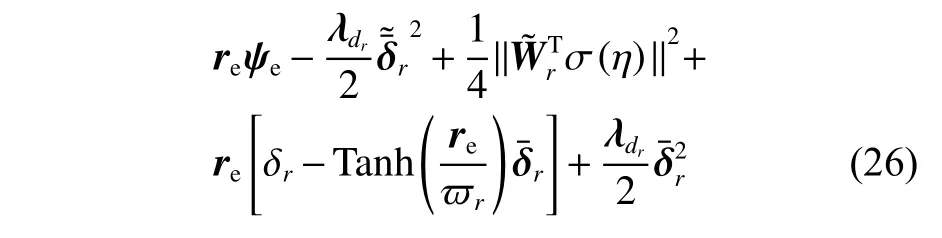
式中， λdu， λdr， ωu， ωr为设计自适应律中的可调参数。

根据引理3，可得

将式(24)、式(28)和式(29)代入式(21)，得

将式(31)代入式(30)，可进一步得出

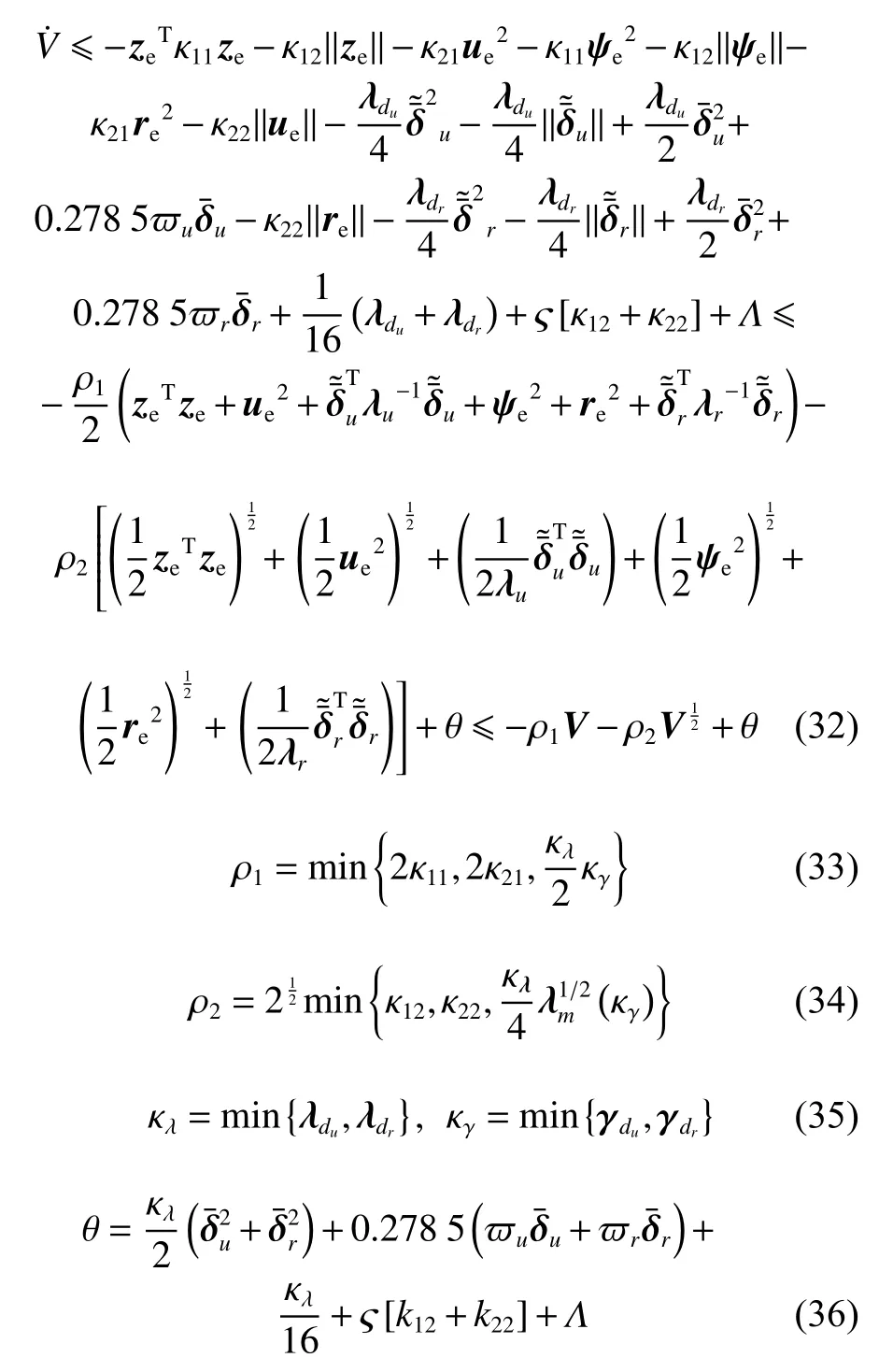
由式(32)，可以得出

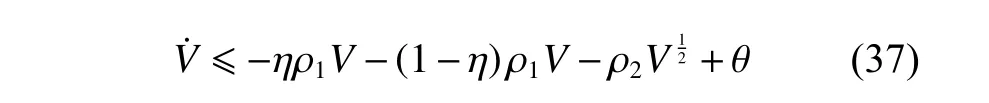
其中， η=min{η1,η2}，0 ＜η ＜1。

结合式(22)，以上计算证明对于 ∀t≥T，系统误差会在有限时间内收敛。

4 仿真研究

为了验证本文所设计控制方案的有效性，以挪威科技大学的Cybership 2船模为被控对象进行计算机仿真试验。该船模总长L= 1.255 m，质量m= 23.8 kg，其他水动力参数详见文献[22]。

在仿真分析中，将本文设计的控制方案与未采用有限时间的自适应神经网络控制方案进行对比。在仿真图中，将本文设计的控制律设为控制律1，用于对比的控制律设为控制律2，对比控制律的虚拟控制律、控制律和自适应律如式(40)～式(43)所示。

为了模拟海况，扰动采用式(44)：

在模型参数未知的条件下，设置参数k11=0.1，k12=0.1，k21=0.2 ，k22=0.1，k31=0.2，k32=0.05，k41=0.4，k42=0.05，γdu=0.1， γdr=1，λdr=1，γwu=γwr=200 ，λwu=λwr=0.002 5。仿真试验采用圆形轨迹方程，如式(45)所示。

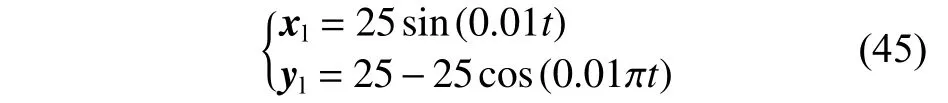
在圆形轨迹下，船舶的初始位置和初始速度为(x0;y0;ψ0;u0;v0;r0)=(0;10;0;0;0;0)。图2～图9 所示为圆形轨迹下的仿真结果。其中，图2 所示为控制律1 和控制律2 的实际轨迹与参考轨迹的轨迹跟踪对比，从中可以看出，本文控制方案下的实际轨迹在有限时间内更接近于参考轨迹。

图2 船舶在平面内的实际轨迹和参考轨迹Fig. 2 Actual and reference trajectories in ( x,y) plane

图3～图6 给出了船舶在不同控制律下的位置跟踪、航向角跟踪以及速度跟踪的对比。从中可以看出，本文设计的控制器可以保证在有限的时间内更接近于期望轨迹。

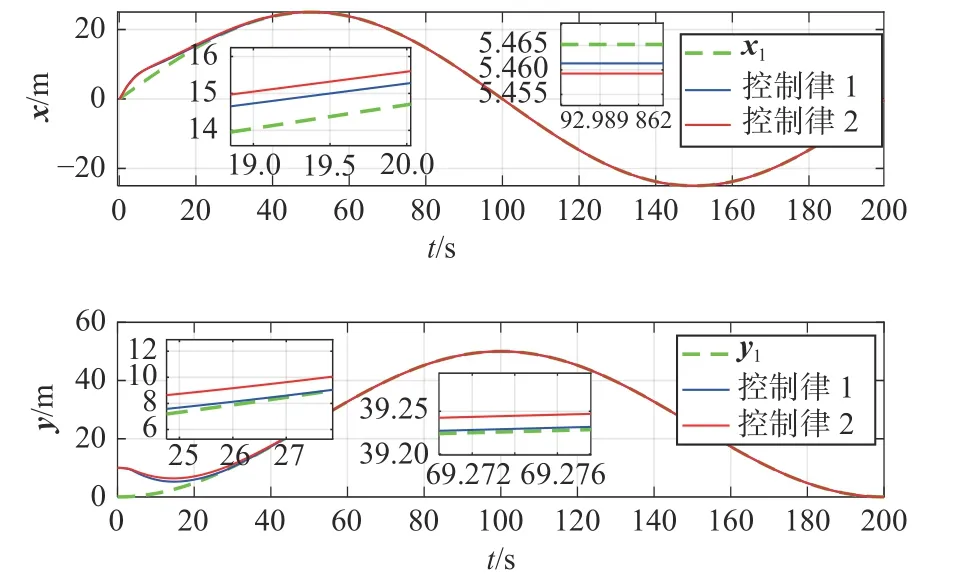
图3 实际位置和参考位置Fig. 3 Actual and reference positions

图4 实际航向角和期望航向角Fig. 4 Actual and reference yaw angles

图5 推进速度uFig. 5 Surge velocityu

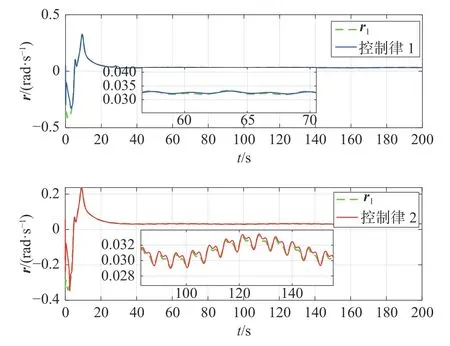
图6 转艏角速度rFig. 6 Yaw angle rate r

图7 所示为位姿误差时历曲线。从中可以看出，本文所设计控制方案误差的上、下界更小，并且在本文设计的有限时间控制方案下，xe和ye约在第29 s 处实现收敛， ψe约在第10 s 处实现收敛，而对比方案的位姿误差则分别约在第50，55 和28 s处实现收敛，可见本文控制方案的收敛速度更快。

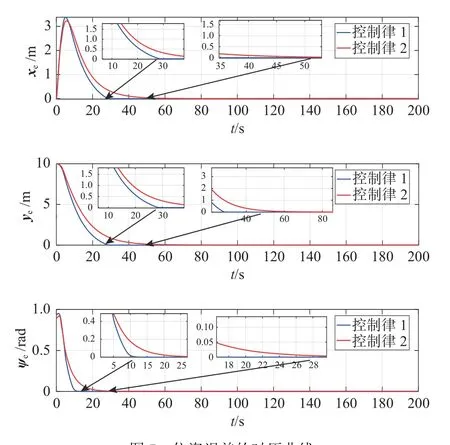
图7 位姿误差的时历曲线Fig. 7 Time history curves of the attitude error

由图8 所示的速度误差时历曲线可以看出，本文所设计控制方案速度误差的收敛性得到了一定程度的提高，其上、下界同样也更小。

图8 速度误差的时历曲线Fig. 8 Time history curves of the velocity error

图9 所示为控制输入随时间变化的曲线。从中可以看出，本文设计的控制律输入与对比控制律相比，没有明显的增加。

图9 控制输入τu，τrFig. 9 Control input of τu，τr

5 结 语

本文提出的自适应神经网络有限时间轨迹跟踪控制方案解决了欠驱动船舶在轨迹跟踪中存在的未知干扰和动态不确定问题，提高了系统的控制精度以及系统误差的收敛速度。利用径向基神经网络重构未知动态，设计了自适应律逼近外部干扰的上界。通过Lyapunov 理论，证明欠驱动船舶系统所有的信号都是有界的。经与未采用有限时间的自适应神经网络控制律进行仿真对比，表明本文设计控制方案的跟踪性能更好。下一步，将就如何在提高跟踪精度的同时简化算法的复杂程度方面进行研究。