基于门控循环单元神经网络的箱型梁结构裂纹损伤检测方法

骆撷冬，马栋梁，张松林，王德禹

上海交通大学 海洋工程国家重点实验室，上海 200240

0 引 言

船舶在生产和服役的过程中会受到例如焊接、疲劳等多种因素的影响而产生裂纹[1-2]，并且在海洋复杂的载荷作用下，裂纹还会扩展，最终使结构断裂，从而引发灾难性的事故。

为了及时发现船体结构损伤，避免安全隐患，学者们提出了多种损伤检测方法，其中结构健康监测技术（structural health monitoring，SHM）可以实现结构安全的实时在线检测。Lindemann 等[3]设计了一种基于概率方法的船体监测系统，完成了对船舶结构监测技术的初步探索。大连新船重工在国内首次设计出了船体应力监测系统，并安装应用到了300 000 t 级VLCC 上[4]。贾连徽等[5]基于船体结构应力实时监测系统，结合整船有限元分析和海况信息，给出了应力监测点的选取方法，并根据监测点的受力特点给出了传感器的布置方法。但随着计算机科学的发展，对船舶结构损伤智能化检测的要求越来越高，传统监测方法的性能已难以满足工程界的需求。

机器学习（machine learning，ML）已被成功应用于计算机视觉、自然语言处理等多个领域，具有非常强大的学习能力，因此许多学者尝试将机器学习应用到结构损伤检测领域，用以提高结构损伤检测能力。Zubaydi 等[6]使用多层感知机（multi-layer perceptron，MLP）检测加筋板的裂纹损伤，并将通过有限元法得到的加筋板振动响应自相关函数以及其一阶导数作为输入，较为有效地识别了损伤的位置和范围。Mehrjoo 等[7]将固有频率和模态振型作为输入，提出了一种基于MLP的损伤检测方法。Palomino 等[8]采用概率神经网络和模糊聚类分析来识别裂纹的位置，证明了该方法的可行性。虽然传统的机器学习与神经网络在损伤检测方面取得了一定的研究成果，但仍存在诸多不足，如收敛速度慢、检测精度低，且性能过于依赖输入特征，对噪声的敏感性较高等[9]。

近年来，深度学习（deep learning，DL）凭借其优秀的学习能力得到了许多研究者的关注，并被应用到了船体结构损伤检测领域。在众多深度学习模型中，循环神经网络（recurrent neural network，RNN）可以处理时间序列，并且有“记忆”的功能，因此在结构的实时损伤检测方面扮演着重要角色。长短期记忆（long short-term memory，LSTM）神经网络是一种改进的循环神经网络，其解决了可能出现的梯度消失和梯度爆炸问题[10]，能够更为有效地处理长期、复杂的时间序列。Zou 等[11]利用集合经验模态分解预处理原始振动信号，得到了将故障特征信号输入到LSTM 中来诊断滚动轴承的故障情况，但该方法是通过人工来提取损伤特征信号，难以保证信息的完整性，且还依赖于特征提取的方式。Ma 等[12]提出了一种基于卷积神经网络（convolutional neural network，CNN）的加筋板裂纹损伤检测方法，张松林等[13]使用LSTM建立了矩形板裂纹损伤检测模型，但他们均未对训练集以外的损伤情况进行近似检测研究。

LSTM 模型有许多变体，其中以Cho 等[14]提出的门控循环单元（gated recurrent unit，GRU）最为著名。GRU 改变了LSTM 的神经元结构，其不仅保留了LSTM 神经网络的长期记忆能力，还让其自身的内部结构更简单，这对特征不是特别复杂的数据来说有着更好的收敛性。Zhao 等[15]首先在时间序列数据中提取了局部特征，随后通过双向GRU 神经网络预测了机器的状态，并在齿轮箱、轴承等故障检测中验证了算法的有效性。薛阳等[16]提出了一种结合CNN 和GRU 的超短期风电预测模型，其将气象数据作为输入，根据风速和风力的发电功率特性，实现了更高精度的风电预测。

目前，已有部分研究者基于GRU 神经网络，针对轴承、齿轮等机械结构的损伤检测进行研究，但少有学者将其应用到船舶结构上。船舶本身结构虽然复杂，但其本质上还是一种箱型梁结构[17]。本文拟以某箱型梁结构为研究对象，提出一种基于GRU 神经网络的裂纹损伤检测方法。由于对结构进行损伤检测时加速度信号能够反映整体和局部的健康状况，因此将选取加速度响应作为输入，通过GRU 神经网络提取损伤特征并进行分类，从而实现对箱型梁裂纹损伤的实时检测。

1 GRU 神经网络

GRU 的结构如图1 所示。图中，t为时刻，xt为当前时刻的输入，ht-1，ht分别为上一时刻和当前时刻的输出，最终，形成一个具有“记忆”功能的“细胞”。细胞内有2 个门控单元，分别是更新门（update gate）和重置门（reset gate），二者共同作用，控制GRU 的更新和储存记忆。两个激活函数分别表示如下：

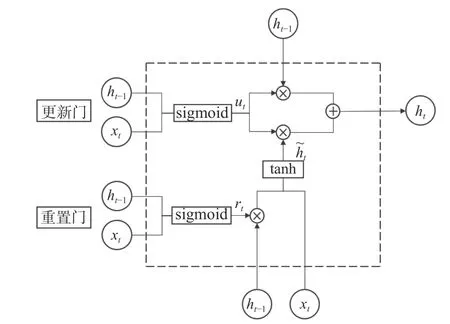
图1 GRU 结构Fig. 1 Structure of GRU

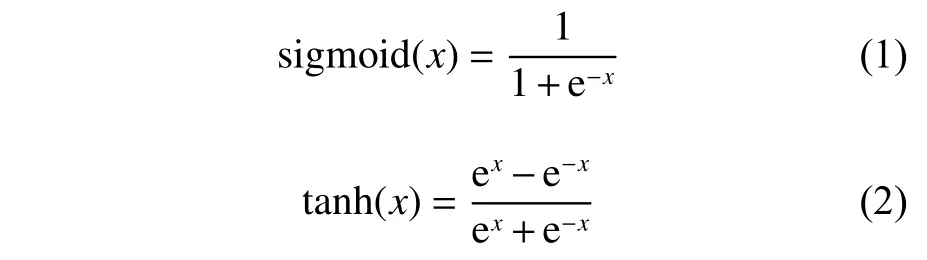
为了实现记忆功能，2 个门控单元的输入都是上一时刻的输出ht-1和当前时刻的输入xt。其中，更新门ut控制上一时刻输出的信息流入到当前时刻的数量。

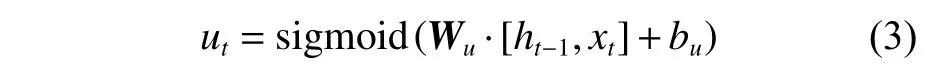
式中：Wu为权重矩阵；bu为偏置项。当ut=0时，输入全部流入当前时刻；当ut=1时，则全部被丢弃。

重置门rt控制上一时刻输出的信息被遗忘的数量以及当前时刻输入的信息被添加的数量。

这里，rt越小，忽略的ht-1越多。而后，再通过激活函数tanh，形成由重置门控制的当前时刻的候选输入为

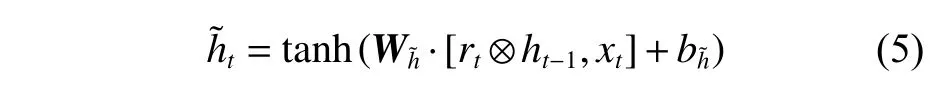
最终，由两部分相加得到当前时刻的输出ht为

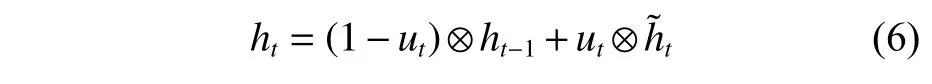
式（6）中，前一部分是通过1 减去更新门ut来控制上一时刻的输出ht-1，另一部分则是通过更新门ut来控制当前时刻的候选输入。

对裂纹损伤的检测除了需要通过大量的GRU 神经元提取损伤数据的特征，还需要对所有特征通过标签进行分类。本文采用的分类函数为Softmax 函数，又称归一化指数函数。

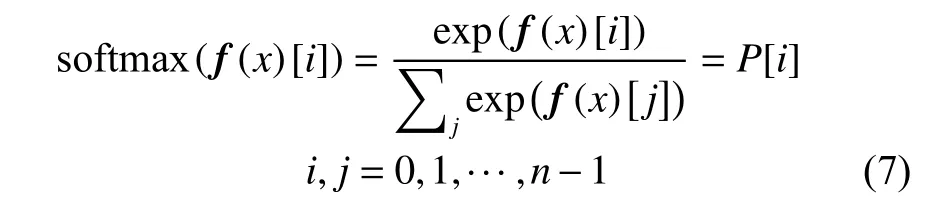
Softmax 函数是将向量f(x)中的每个元素变换为向量P中的对应元素P[i]，并且是以概率的形式展现出来。P[i]越大，则实际裂纹标签为i的概率越高，最终将P中最大元素P[k]的标签k认定为预测的裂纹标签。

通过Softmax 函数得到预测的裂纹标签后，还需要根据预测标签与实际标签的误差来得到损失值，并利用损失值的大小来证明神经网络模型的鲁棒性。本文使用的损失函数为交叉熵损失函数（cross entropy loss）。

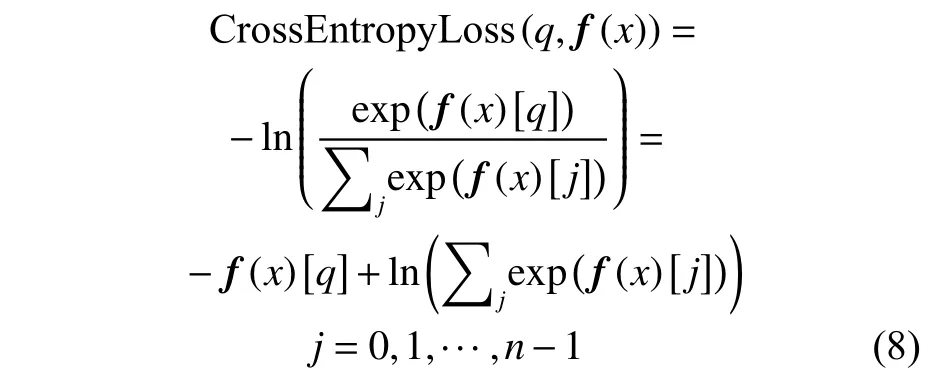
式中：q为板裂纹的实际标签值；f(x)为神经网络模型的实际输出。

综上，GRU 模型是以得到最小的损失函数值为目标进行训练，最终获得对数据的预测结果。

2 箱型梁裂纹损伤检测分析

2.1 有限元模型

GRU 神经网络的训练需要大量数据，Law 等[18]通过试验证明了采用有限元方法计算结构加速度响应的准确性与可靠性，因此，本文将采用Python语言对ABAQUS 软件进行二次开发，建立箱型梁结构的有限元模型并计算加速度响应。

本文研究的箱型梁模型长L= 2 160 mm，宽度和深度为B=D= 1 200 mm，厚度t1= 5 mm，模型如图2（a）所示。同时，在顶板与底板上分别设2 根均布加强筋，在两侧板上分别设置3 根均布加强筋，加强筋的高度h= 100 mm，厚度t2= 5 mm。采用有限元计算得到的模型前8 阶固有频率分别为79.10 ，87.22，87.66，95.57，96.05，104.07，112.43，115.96 Hz。考虑到箱型梁动态分析中的阻尼效应，本文采用瑞利阻尼（C= αM+ βK，其中M，K分别为结构的质量矩阵和刚度矩阵，C为结构的阻尼矩阵， α， β分别为结构的质量比例阻尼系数和刚度比例阻尼系数）进行模拟[19]。最终选取的材料参数如表1 所示。

表1 箱型梁材料参数Table 1 The material parameters of the box girder

本文所采用模型的边界条件为，将图2（b）所示端面1，2 的所有节点分别与各自端面的形心A，B 进行刚性耦合，并对其中的端面1 放开沿z方向的位移与绕x方向的转角，对端面2 放开绕x方向的转角，2 个端面其他方向的位移与转角则均予以约束。有限元模型的网格尺寸为20 mm × 20 mm，网格单元类型为S4R。

图2 数学模型Fig. 2 Mathematical model

实际船舶的受载情况复杂且随机，难以获取。高斯白噪声是一个均值为0 的平稳遍历随机过程，其任意两个值在统计上都是独立的，同时，其功率谱密度是恒定的，可以激发结构的多重模态[20]。因此，本文采用高斯白噪声模拟结构遭受的激励，并施加于箱型梁顶板上。本文所采用的高斯白噪声激励为面外均布载荷，载荷均值为0，标准差为0.01 MPa，对应于一个低程度的载荷水平。载荷的采样频率为10 000 Hz，按对应时间点施加于板上，共施加4 s。由于本文主要关注模型的前8 阶固有频率，因此，采用截止频率为256 Hz的巴特沃斯滤波器（Butterworth filter）对上述载荷进行滤波。

在船舶裂纹中，贯穿裂纹为主要的裂纹形式，可能由疲劳、焊接缺陷等多种因素产生，因此，本文将对发生于顶板和底板的沿板长方向的单裂纹损伤进行研究。对顶板和底板，分别设置了5 个裂纹位置和3 个裂纹长度：每块板上的5 种裂纹位置等距分布；3 个裂纹长度L1分别为120，240，360 mm。考虑到模拟的是实际裂纹，同时便于网格划分，因此采用菱形裂纹，其最大宽度为0.1 mm。顶板裂纹的位置和形状如图2（c）所示，底板裂纹的位置和形状与顶板相同。由于加速度响应在裂纹附近位置处变化更明显，因此在顶板和底板上分别设置了11 个加速度采集点，将采集到的结构加速度响应作为神经网络的输入数据。当采集点与裂纹位置重合时，采集裂纹中心位置上侧节点的加速度响应。顶板的11 个加速度采集点如图2（d）所示，底板的采集点与顶板相同。

2.2 原始数据处理

考虑到结构在初始振动阶段会受到自由振动的影响，因此针对无裂纹的箱型梁的自由振动进行分析，通过在顶板上施加均布瞬时激励，得到其顶板中心位置在0～2 s 时间范围内的加速度曲线如图3 所示。由图可以看出，箱型梁在初始阶段存在明显的自由振动，并以较快的速度衰减，可以认为1 s 后自由振动基本消失。因此，本文将仅采集1～4 s 内的加速度数据。考虑到采样定理，为保证信号信息不丢失，采样频率需大于等于2 倍的信号频率（即2.1 节所述的256 Hz 截止频率），因此，本文设置的加速度采集点的采样频率为512 Hz，最终，每个采集点得到的数据长度为1 536。

图3 无损箱型梁自由振动曲线Fig. 3 Free vibration curves of an intact box girder

由于采用有限元计算所得原始加速度数据存在量级不统一的问题，为便于GRU 神经网络能够更加高效地学习到数据的特征，提高精度，可对采集到的数据进行高斯归一化处理[20]。高斯归一化可以将原始数据变换成均值为0、标准差为1、服从标准正态分布的数据集：

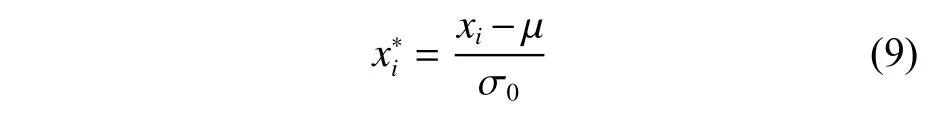
式中：xi为原始数据；μ和σ0分别为原始数据的均值和标准差；为变换后得到的归一化数据。

由于载荷的施加位置为顶板，由图3 可见，顶板和底板处的加速度响应大小有一定的差距，因此，将顶板和底板的加速度数据分别进行了高斯归一化处理。此外，考虑到在实际的裂纹损伤检测工作中，由于受外部环境、采集设备等多种因素的影响，噪声的影响不可避免，因此对处理后的数据增加了均值为0、标准差为0.3 的高斯白噪声，并针对无噪声和有噪声的数据训练结果进行了对比分析。

2.3 数据集的生成

本文的数据处理和数据集的生成流程如图4所示。

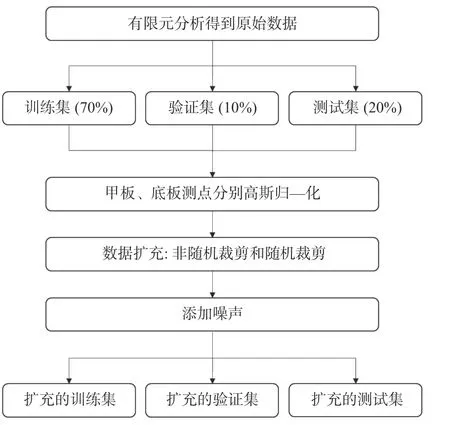
图4 数据处理与数据集生成流程Fig. 4 Data processing and data set generation

首先，通过对有限元模型进行多次计算，得到足够多的原始数据。本文针对单裂纹损伤进行研究，研究的工况共31 个（10 个裂纹位置 × 3 个裂纹长度 + 1 个无损工况），随后对每个有裂纹模型分别计算30 次，无损工况计算100 次，最终得到1 000 组原始数据。对于每一次计算，为保证样本的有效性和随机性，施加于结构上的都是随机生成的高斯白噪声激励，两两之间各不相同。

由于GRU 神经网络的运行需要的数据集包括训练集、验证集和测试集，同时为保证各数据集的独立性，在数据处理的最初阶段，先将原始数据中的有损工况、无损工况分别按7:1:2 的比例分为训练集、验证集和测试集，然后分别按2.2 节所述方法对原始数据进行处理，消除自由振动的影响并进行高斯归一化，随后再采用数据扩充的方法对样本数据进行扩充，最终得到完整的数据集。

本文通过数据裁剪的方法进行数据扩充，数据裁剪方法可分为非随机裁剪和随机裁剪2 类。其中非随机裁剪指将高斯归一化后的1～4 s 时间范围内长度为1 536 的数据平均分成三等分；随机裁剪则是从高斯归一化后的数据集中随机选取若干样本，然后再从每个样本上随机裁剪一段长度为512 的数据。将由这2 种方法得到的样本汇总为完整数据集，数据集中的样本总数被扩充至14 520 个，其中训练集、验证集、测试集的样本数分别为10 164，1 452 和2 904 个。每个样本的数据形状为1×512×22，样本数据尺寸的第1 个维度表示数据的高度；第2 个维度表示数据的长度，对应的采样频率512 Hz；第3 个维度表示数据深度，本文通过数据采集点数来表示数据深度，对应22 个加速度采集点。

2.4 GRU 神经网络结构及参数设置

本文通过GRU 神经网络对箱型梁进行裂纹损伤检测。该神经网络共有1 层输入层，3 层隐藏层，1 层输出层，其结构如图5 所示。图中：a为输入的损伤数据，即箱型梁测点的加速度响应，其数据结构为b×t×d，其中b为批处理大小，即每次迭代的样本数量，t为时间步，即输入数据的时间长度，d为每个时间步输入向量的特征维度；h为GRU 层提取的损伤特征，用于确定裂纹的位置和长度；P[i]为最终的输出数据，即损伤在各标签下的概率。

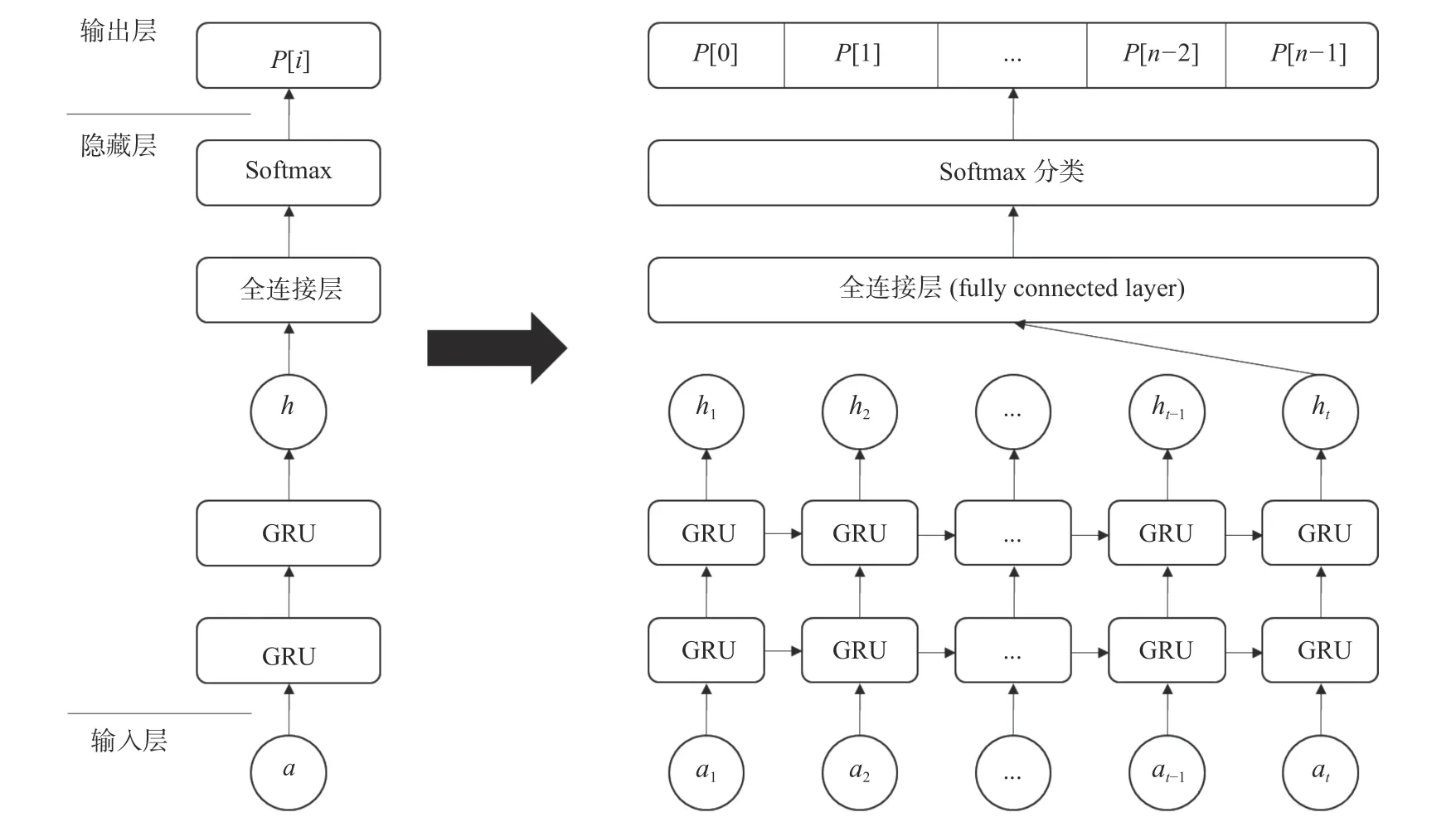
图5 GRU 神经网络模型结构Fig. 5 The structure of the GRU neural network model

隐藏层包含2 层GRU 神经网络层和1 层全连接层，其中GRU 神经网络层用于从输入数据中提取损伤特征，全连接层则对提取到的损伤特征进行处理并输入到Softmax 函数中进行分类。同时，为避免模型出现过拟合现象，本文在GRU 层间加入了Dropout 算法，可以让模型按照一定的概率舍弃部分神经元，避免依赖数据的局部特征进行输出[21]。

在本文中，输入数据a代表一批加速度数据，ai代表这批加速度数据按照时间步展开后各时刻的加速度数据。输入数据首先输入到前一层GRU 神经元进行计算，并将前一层GRU 神经元的输出作为后一层的输入，可以认为模型在每一时刻同时学习到的是22 个不同采集点的加速度数据，连续学习了512 个时间步。然后，将最后一层GRU 神经元最后时刻的输出作为全连接层的输入，并通过Softmax 函数进行分类，输出模型预测的裂纹标签。

神经网络需要设置合适的超参数，GRU 神经网络的超参数主要包括学习率、模型训练次数、批处理大小、输入层维度、隐藏层特征维度、循环层数、输出层维度、舍弃概率等。其中，学习率指神经网络模型学习数据特征的速度，这决定了目标函数能否以及如何收敛至局部最小值；训练次数（epoch）指使用训练集的全部数据对模型进行完整训练的次数；批处理大小、隐藏层特征维度已在本节开头进行论述；输入层维度指样本的数据深度，对应22 个加速度采集点；循环层数指本文采用的2 层GRU 层；输出层维度取决于研究的内容，如裂纹位置、裂纹长度等；舍弃概率指Dropout 算法按该概率舍弃的部分神经元。

经过多次测试，本文GRU 神经网络使用的超参数值如表2 所示。此外，为帮助模型更好地收敛而得到最优解，本文还在GRU 神经网络中加入了Adam 优化算法，并以指数衰减的形式更新了模型的学习率：

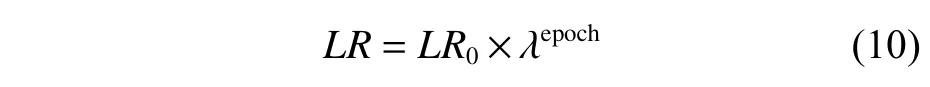
式中：LR为 当前训练批次的学习率；LR0为初始训练批次的学习率，如表2 所示，为0.01； λ为衰减常数，本文选取为0.95。

表2 GRU 模型超参数Table 2 The hyperparameters of the GRU model

2.5 模型性能验证

为了验证GRU 神经网络模型的性能，本文采用基于小波包变换的多层感知机神经网络（WPTMLP）[22]进行了对比。本文所采用WPT-MLP 方法的小波包基函数为Daubechies wavelet 2(Db2)，分解层数为4 层，将22 个采集点的加速度响应中的损伤特征提取出来，并将1×(22×512)的加速度数据提取为1×(22×16)的特征样本。然后，再由多层感知机（MLP）训练得到裂纹损伤预测结果，该MLP 的结构和前文所提GRU 的结构相同，并采用同样的数据集、全连接层、优化函数、分类函数及损失函数等。

3 裂纹损伤预测结果

本文采用GRU 和WPT-MLP 这2 种方法，将分别针对裂纹的位置和长度进行研究，同时，还需针对每个样本分别设置一个标签，标签数量与输出层维度相等。此外，还分别将裂纹的位置和长度不在训练集中的情况用于测试，以验证GRU 模型对裂纹损伤的近似预测能力。

3.1 裂纹位置预测

针对裂纹的位置进行研究时，输出层维度为11，标签“0”代表无损工况，“1～5”代表图2（c）中顶板的5 个裂纹位置，“6～10”代表底板对应的5 个裂纹位置。经过对神经网络模型的训练、验证与测试，最终对裂纹位置的预测结果如表3 所示。从中可以看出，GRU 方法在无噪声情况下对裂纹位置的预测精度达100%，在有噪声的情况下其精度为97.14%，均远高于WPT-MLP 方法的94.63%（无噪声）和76.45%（有噪声）。可见GRU方法具有更优的裂纹位置检测性能，且对噪声的敏感性较低。

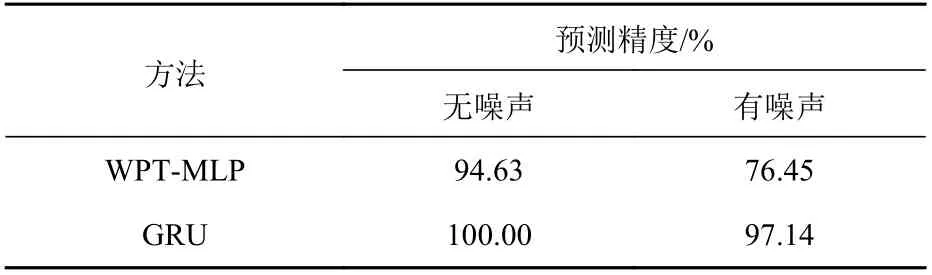
表3 裂纹位置预测精度Table 3 The prediction accuracy of crack location

同时，为了更直观地分析神经网络模型对每一个裂纹位置的预测情况，本文采用混淆矩阵彩色刻度展示了有噪声情况的结果。混淆矩阵中的元素越向主对角线集中，说明预测的效果越好。对裂纹具体位置预测结果的混淆矩阵如表4 和表5 所示，其中的行和列分别表示裂纹的预测位置和实际位置。从中可以看出，相比WPT-MLP方法，GRU 方法对各个位置的预测更准确，仅对无损状况的预测精度较低，约为91%。

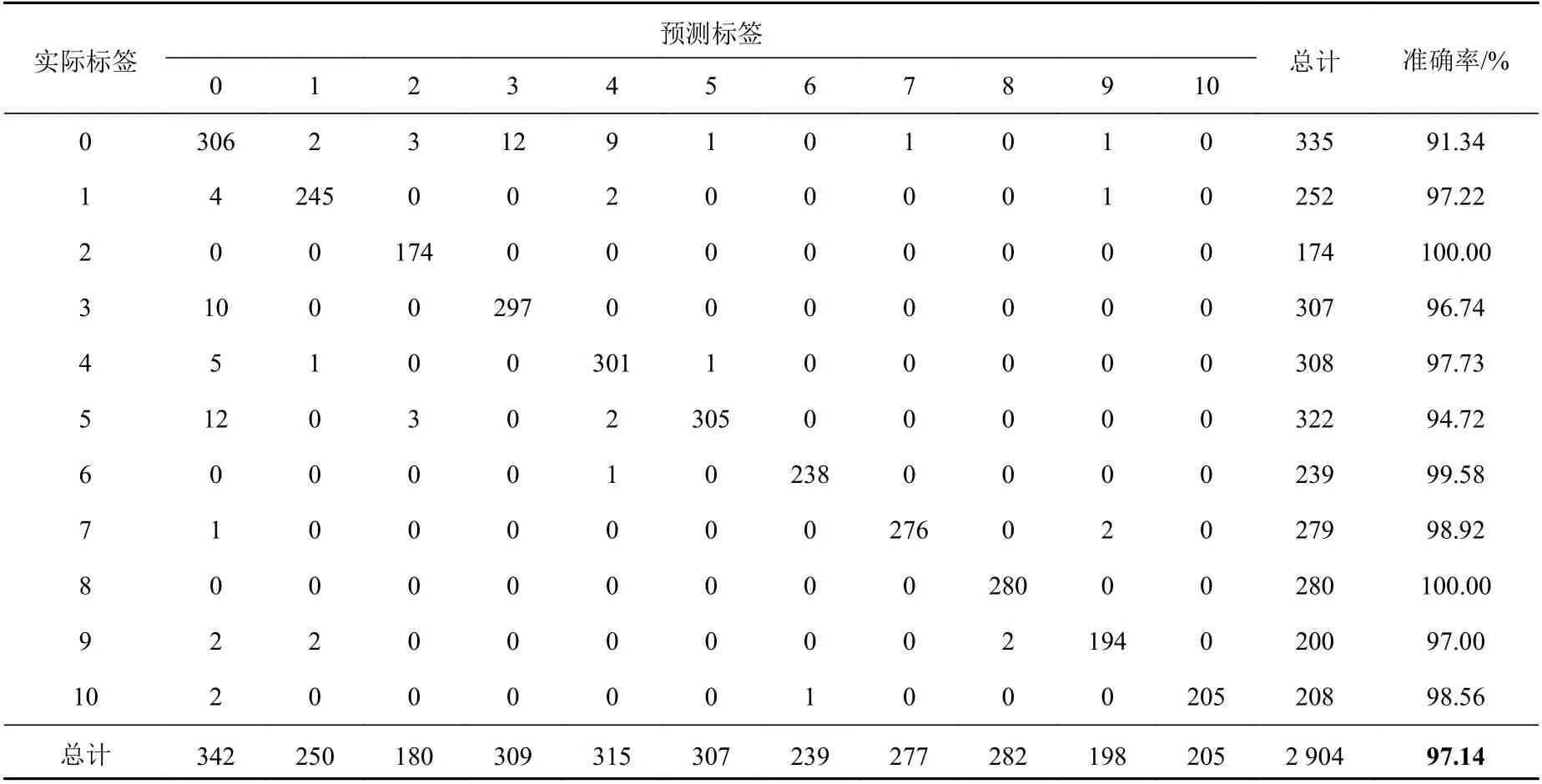
表4 有噪声情况下GRU 方法对裂纹具体位置预测的混淆矩阵Table 4 Confusion matrix of crack location prediction using GRU method with noise

表5 有噪声情况下WPT-MLP 方法对裂纹具体位置预测的混淆矩阵Table 5 Confusion matrix of crack location prediction using WPT-MLP method with noise

3.2 裂纹长度预测

对裂纹长度进行研究时，输出层维度为4，标签“0”代表无损工况，“1～3”分别代表裂纹长度为120，240，360 mm。最终，对位置的预测结果如表6 所示。由表可见，GRU 方法在无噪声情况下对长度的预测精度达96.38%，在有噪声情况下精度为88.67%，可见采用GRU 方法的定长精度明显优于WPT-MLP 方法，可以有效提取裂纹长度损伤特征。

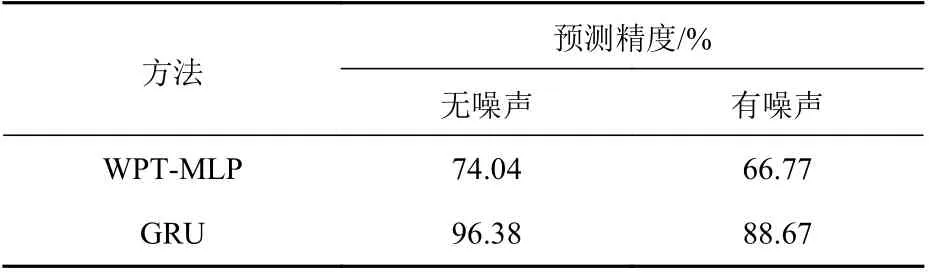
表6 裂纹长度预测精度Table 6 The prediction accuracy of crack length

对裂纹长度的预测结果混淆矩阵如表7 和表8所示。从中可以看出，WPT-MLP 方法对损伤长度的预测不够理想，远不及GRU 方法，且难以预测出无损状况；GRU 方法对各个损伤长度的预测比较准确，但对无损状况的预测精度较低。同时，GRU 方法预测错误的情况主要集中在无损和120 mm 长度裂纹的相互识别上，可见无损与低损伤状态的特征具有一定的相似性。

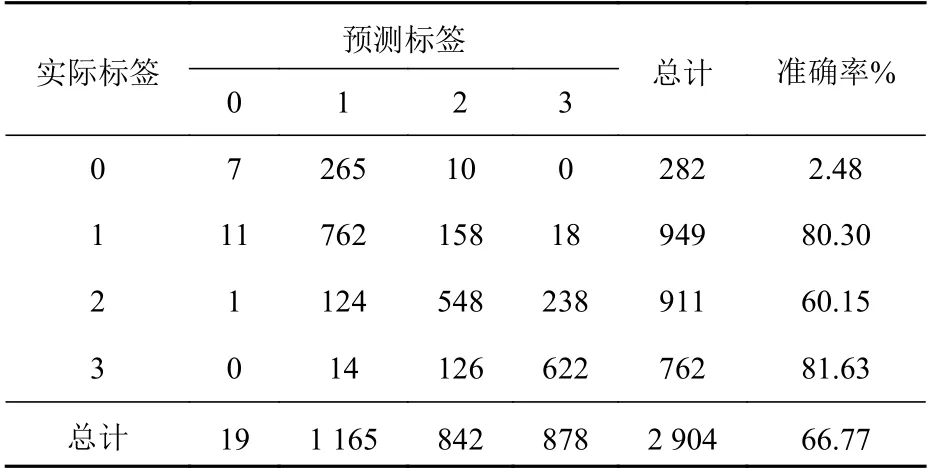
表8 有噪声情况下WPT-MLP 方法对裂纹长度预测的混淆矩阵Table 8 Confusion matrix of crack length prediction using WPT-MLP method with noise

3.3 裂纹近似预测

上文已验证GRU 模型对损伤的位置和长度这2 个维度均具有较高的预测精度，本节将在已完成的长度预测的基础上，验证模型对位置的近似预测能力，即针对裂纹位置不在训练集测点（3.1 节所述10 个位置）时，进行无噪声和有噪声这2 种情况下的近似预测。

假设已通过长度预测得到裂纹长度为360 mm，随后进行裂纹位置的近似预测。选取裂纹中心在底板6 号和7 号中间的5 个等距位置A～E 上，如图6 所示，然后分别将其有限元计算结果数据经过2.2 节所述处理后作为GRU 模型的测试集。同时，由于已确定裂纹长度，因此训练集和验证集中可以只保留无损工况和标签“0～10”每个位置长度为360 mm 的计算结果。

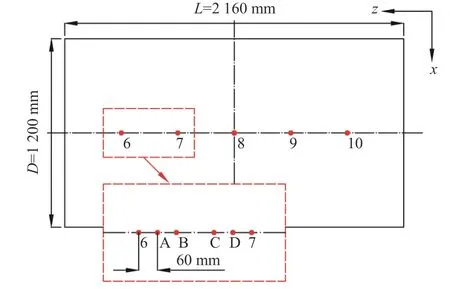
图6 裂纹位置近似预测测点Fig. 6 Measuring point for approximate prediction of crack location

由于选取的测点A～D 位于6，7 号位置中间，因此，本文关注模型将测点加速度响应数据识别为 6，7 号的概率。最终的测试结果如图7 所示，由图可见，GRU 模型可以以较高的精度将训练集以外的位置近似预测到与其最接近的训练集测点，且距离训练集测点越近，预测的准确率越高。针对有噪声的情况，当测点距离训练集位置60 mm 时，近似预测的精度可以超过90%。同时还发现，在噪声的掩盖下，模型的近似预测能力有所下降，且降幅随关注点距训练集测点距离的增大而增大。可以采取提高训练集测点密度的手段来降低噪声的影响。

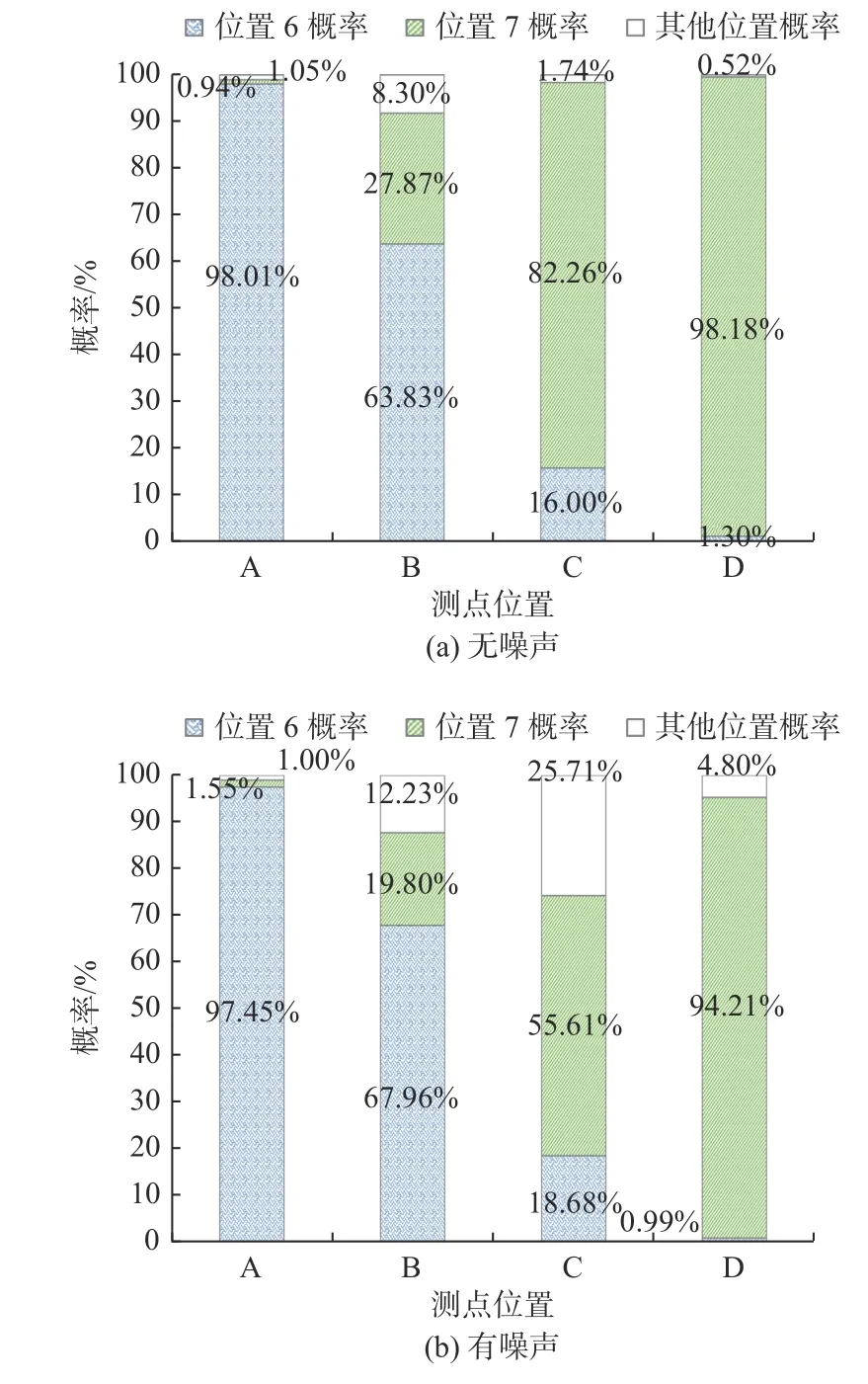
图7 裂纹近似预测结果Fig. 7 Results of approximate prediction of crack

4 结 论

本文提出了一种基于GRU 神经网络的箱型梁结构裂纹损伤检测新方法，其可以同时检测箱型梁不同位置处的裂纹位置和长度。首先，通过Python 语言对ABAQUS 进行二次开发，建立结构有限元模型并计算得到的加速度响应；然后通过数据扩充得到GRU 模型的输入数据集，对裂纹位置、长度进行研究并与WPT-MLP 方法进行对比；最后，对模型的近似预测能力予以验证。文章主要得到如下结论：

1） GRU 方法的裂纹损伤特征提取能力强，可以较准确地预测裂纹位置及长度，并具有良好的抗噪声能力，其各方面的性能均优于WPT-MLP方法。

2） 低损伤样本（120 mm 长度裂纹）和无损样本的损伤特征具有一定的相似性。

3） 对于训练集之外的其他位置，采用GRU方法也可以较准确地将其识别到最接近的位置，具有较强的近似预测能力。

本文的研究证明了GRU 神经网络在包含多个板的箱型梁结构裂纹损伤检测工作中的适用性，为未来将深度学习应用于实际船舶的损伤检测工作中提供了新的思路。未来，可以在本文研究的基础上继续拓展裂纹种类，拓展检测维度，继续提升GRU 神经网络的性能。