PCA显著性检验结合相关分析的图像缩放法

胡明颖，陶 胜

(集美大学理学院，福建 厦门 361021)

0 引言

传统的非等比例缩放一般分为均值采样和直接裁剪，简单易操作，但是均值采样会造成视觉内容的变形，直接裁剪往往会丢失图像的部分信息。Avidan等[1]开创性地提出基于内容的图像缩放方法——线裁剪(seam-carving,SC)方法，既能实现非等比例缩放，又能保留图像的重要内容。所有内容感知图像缩放方法的关键在于寻找适合于图像的能量图或者显著图。图像的显著图即为图像的显著性区域，即图像中特别能吸引人注意的区域。早期最经典的显著模型是由Itti等[2]提出的基于人类视觉和神经科学自下而上的IT算法，之后，出现了多种显著性检测的算法[3-9]，每种算法遵循不同的显著性规律，得到的显著图各有特点。魏昱[10]提出加权多尺度频率调谐与关键区域聚焦方法(简称FTK算法)和超像素全局对比度与关键区域聚焦方法(简称SPK算法)，进一步提高了SC算法的视觉处理效果，使图像的细节、形态能够得到很好地保留。李晶[11]将基于内容感知显著性检测的CA(context aware)算法[12]与SC算法相结合，采用CA显著图代替线裁剪方法中的能量图对图像进行缩放，更好地保护了显著性目标且图像扭曲较小。

缩放比例不大时，SC算法效果较好，但是基于动态规划的计算使得算法复杂，运行时效不高，同时若缩放比例增大会使图像出现局部扭曲变形。为提升图像缩放效率，降低运行时间，本文引入主成分分析(principal component analysis,PCA)法进行图像的显著性检测，并与相关分析法相结合完成图像缩放，使缩放变化集中在非显著性区域，同时尽量保持背景的平稳光滑过渡，减少人工痕迹，让图像的整体性和可观性得到较好的保护。

1 算法描述

1.1 图像像素的3×3领域构造

显示器终端的图像一般都是RGB颜色模型。本文采用更接近人类视觉系统的CIELab颜色模型，该模型在显著性检测中效果较好。因此，需将图像由RGB颜色模型转为CIELab颜色模型。分别在CIELab颜色模型的L、a、b三个分量通道中，以每点与其周围3×3领域的均值为其特征维度。不失一般性，本文以通道L为例来阐述图像像素的3×3领域构造过程。

假设图像有m行n列，可以用m×n阶矩阵表示该数字图像CIELab颜色模型中的L通道。设点p为位于坐标(x,y)处的一个像素[13]，则p的四个水平和垂直相邻像素的坐标为：(x+1,y)，(x-1,y)，(x,y+1)，(x,y-1)。这4个像素组成p的4邻域，用N4(p)表示，每个像素距(x,y)一个单位距离。像素p的4个对角邻像素的坐标为：(x+1,y+1)，(x+1,y-1)，(x-1,y+1)，(x-1,y-1)。该像素集用ND(p)表示,ND(p)和N4(p)合起来用N8(p)表示,点p与N8(p)构成3×3领域。

1.2 PCA算法的显著性检验

将该列向量矩阵恢复为原图像的m×n阶矩阵S=(sij)m×n，sij表示点(i,j)的显著得分，可得到基于PCA算法的显著图(如图1所示)。

定义图像行、列向量的显著度

PCA算法的显著性检测使得：重要区域特别突出，且缩放产生的形变可以避免或者较少发生在主要物体上；得到的显著图有着很好的边界信息，能够更好地保持物体周围的边界和形状；保留了一定的上下文信息，重要区域与周围环境的显著性有着平稳过渡，减少人工痕迹的影响。

1.3 结合显著图和相关分析的图像缩放

随机变量的相关系数刻画的是变量之间的线性相关程度。对于图像，可以对其灰度图像数字矩阵的各行各列进行相关分析，确定行、列的相近度，衡量它们的相近程度，并结合显著图行列的显著度，加权得到行列的重要值，再对缩放行列进行散化处理，得到缩放图像。

1.3.1 行、列的相近度

1.3.2 基于行、列重要值的图像缩放

图像行、列向量的显著度Srow(i)和Scol(j)反映的是行列在图像颜色、亮度、方向、强度等多方面的信息，显著度越大，越容易被视觉神经识别，即为显著区域，也是在图像缩放中应该保护的重要部分。灰度图像行、列向量相近度Rrow(i)、Rcol(j)反映的是图像行、列向量的相近程度，相近度越大，改变这些行列对图像的影响越小，可依据缩放比例对其进行删除或插入新向量。显著度Srow(i)、Scol(j)和行列的重要性成正比，相近度Rrow(i)、Rcol(j)与之成反比。为此，引入加权函数定义行、列向量的重要值：Frow(i)=(1-μr)Srow(i)+μr(1-Rrow(i)),Fcol(j)=(1-μc)Scol(j)+μc(1-Rcol(j))。其中:显著度权重比μr=(1-Rrow(i))/(1-Rrow(i)+Srow(i))；相近度权重比μc=(1-Rcol(j))/(1-Rcol(j)+Scol(j))。

若图像缩小为m′×n′，则根据行、列重要度Frow(i)和Fcol(j)的升序排列，删除(m-m′)列Fcol(j)较小的列向量和(n-n′)行Frow(i)较小的行向量，即可得到缩小图像。

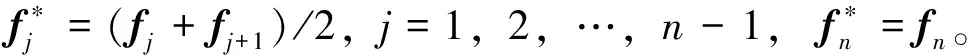
本方法算法简单，但是如果较小的行列重要值连续，即删除或者增加行、列出现连续，得到的缩小图会产生图像扭曲和放大图局部比例失调等问题。为此，需要对重要值进行调整，散化可能连续的形变行、列向量。调整第j列相邻两列的重要值为

第(j-1)、(j+1)列的重要值得到提高，可避免连续删除，行向量同理散化。

为了方便对比，现将图像缩放的行、列灰值设置为零，即将缩放行列标注线设为黑色，见图2。

图2原图的分辨率为500 px×375 px，缩小为450 px×330 px的图像，即删除45行50列。为方便说明，同样增加45行50列，放大尺寸为550 px×420 px。从散化前的图2a可以看出，缩放行列均避开了显著区域，使得缩小图(图2b)和放大图(图2c)的形变均发生在背景图像上。但是，散化前图2a缩放行列发生了连续，缩小图(图2b)右侧显现不连续且下方信息丢失；放大图(图2c)右侧和下方出现明显的比例放大失调。而散化后的对比图，对上述情况都做出了很好的调整，既保证了主体的完好又使得背景过渡平滑自然。

2 实验结果与分析

本实验的软件和硬件环境如下：处理器AMD Ryzen5 4600U,内存16 GB，软件版本Matlab2018。采用分辨率不同的三张图像：5000 px×355 px，299 px×400 px，500 px×501 px。分别与传统的均值采样和直接剪裁比较缩放效果，与经典的SC算法比较运行速度和大比例缩放性能。

2.1 效果比较

图3a分辨率为500 px×355 px，分别采用均值采样法、直接裁剪法和本文方法将图像缩小为355 px×355 px的正方形图像。对比发现，均值采样因为没有考虑显著区域，所以删除145列时造成了主体花朵的横向变形严重；直接裁剪根据比例直接删除了非显著区域的145列，保留了花朵的完整部分，但是造成了图像内容的不完整，丧失了过多次要信息，容易造成图像解读错误；本文方法保留了显著部分，结合相关分析，删除了信息高度重叠的列向量，通过散化改进使缩小图呈现基于内容缩放的整体效果。

图4a分辨率为299 px×400 px,现分别采用均值采样法、直接裁剪法和本文方法将图像放大为400 px×400 px的正方形图像。均值采样根据放大比例直接均匀插入了101列，很显然，图像的主体宫殿随之发生横向变形，比例失调，破坏了整体结构；直接裁剪是无法实现放大图像的；本文方法在重要值较低的两侧均匀增加了101列，既实现了放大的效果，又保证了主体的概貌特征和比例。

传统的均值采样(scaling)可以实现非等比例的缩小和放大，操作简单但是易发生图像变形；直接裁剪(cropping)只能实现非等比例的缩小，无法做到放大，而且很容易损失图像信息，造成图像的视觉误解。本文方法既可以实现图像非等比例的缩放，同时因为采用了显著图，又可以很好地保护显著区域，散化重要度的改进使得缩放图像整体概貌良好。由以上对比分析可知，有效的显著区域检测是内容感知的图像缩放的前提，只有将良好的显著图和缩放算法相结合才能得到效果较好的缩放图像。

2.2 性能比较

图5a的分辨率为500 px×501 px，采用SC算法[1]和本文方法分别将图像缩小为450 px×450 px。SC算法在能量图(图5b)中选择水平能量线51条、垂直能量线50条进行裁剪，最终得到缩小图图5c。本文方法除了考虑显著图还结合相关分析，选出重要值最小又不连续的51行和50列直接删除，得到图5e。

两种方法的缩小图(图5c、e)的效果无明显差异，都较好地保护了主体内容且背景过渡自然，没有人工痕迹，但是本文算法的计算复杂性显著降低，运行速度明显提升。为了做出更多对比，将上文已出现的4幅图像分别采用SC算法和本文算法，缩小两种尺寸，第一组缩小30行30列，第二组缩小60行60列，结果见表1。

表1 运行时间对比图

从两种方法的运行时间可以看出，本文方法确实提高了运行时效。同时，通过两组不同比例的缩小速度可以看到，当比例增大时，SC算法的速度下降明显，而本文方法趋于平稳。可见，SC算法对于较小比例的缩放效果和本文方法相近，但是运算繁琐。本文删除和增加像素的方式与SC算法相似，但是本文采用显著图PCA算法和相关分析取代SC算法(能量图)，不仅计算简单，运行高效，也有效改善了当缩放比例较大时，图像会局部变形的问题。

3 结论

本文提出一种将主成分分析的显著性检测引入基于内容感知的图像缩放算法。首先计算图像行列的显著度，再结合行列相近程度度量的相关系数，定义各行各列的重要值并升序排列，删除前若干行、列向量，或者在前若干行、列向量后增加相邻均值向量，并通过散化连续缩放行列，得到缩放图。实验结果表明，与传统缩放方法比较，本文算法既可以保护显著区域又可以获得良好的整体视觉效果；而与经典的内容感知图像缩放SC算法相比，本算法更简洁，运行更高速。