基于新陈代谢灰色马尔科夫模型的芜湖港集装箱吞吐量预测

朱经君,兰培真,徐圣豪

(1.安徽中澳科技职业学院国际商务系，安徽 合肥 230001；2.集美大学航海学院，福建 厦门 361021；3.福建船政交通职业学院，福建 福州 350007)

0 引言

港口集装箱吞吐量具有波动性大、受国内外环境影响大等特点。近年来，相关学者在港口集装箱吞吐量预测方法上做了大量的研究：王振振等[1]使用加权灰色关联分析和ES-Markov组合模型，对深圳港集装箱季度吞吐量进行预测，解决了集装箱预测的季节性波动问题，为港口集装箱吞吐量预测提供了依据；高妍等[2]提出了多元序列的Jackknife模型平均(JMA)方法，运用序列之间以及序列自身相关性的度量，利用逐步向前法确定候选VAR模型；杨波等[3]构建逻辑斯蒂增长模型的多因素动态生成系数法，对天津港、上海港及青岛港相关年份的港口集装箱吞吐量进行预测研究；杜柏松等[4]构建无偏优化的灰色GM(1,1)马尔科夫动态模型，对上海港集装箱吞吐量进行预测研究，虽然简化了计算过程，但忽略了实际误差与中间值的偏离。对于沿海港口集装箱吞吐量预测，相关学者取得的成果颇丰，但多数研究需要大量的原始样本，且对于内河港口波动的数据预测较少。现实生活中很多的体系都具有灰色性，都符合灰色系统的特征，集装箱吞吐量也具备灰色系统的特征。考虑到单一预测方法的预测精度不够准确或没有对比性。本研究利用芜湖港2011—2020年集装箱吞吐量数据，分别构建灰色GM(1,1)模型及新陈代谢灰色GM(1,1)模型，并运用马尔科夫模型分别对两个GM(1,1)模型的预测数据进行修正，试求提高集装箱吞吐量预测的精确度，以此为芜湖港的主管部门和港口物流企业进行港口规划提供数据支持，从而提高港口运营效率、降低港口运营成本、促进港口经济可持续性发展。

1 新陈代谢灰色GM(1,1)马尔科夫模型

1.1 灰色GM(1,1)模型

本文首先构建芜湖港集装箱吞吐量GM(1,1)预测模型。设芜湖港集装箱吞吐量原始数列为：x(0)=(x(0)(1),x(0)(2),…,x(0)(n))。

对原始数列x(0)=(x(0)(1),x(0)(2),…,x(0)(n))再次运用文献[5]中的灰色GM(1,1)模型计算公式，做1次累加(AGO)生成数列，通过求均值数列、建立白化微分方程、解方程、累减还原得预测值等求解步骤，得到芜湖港集装箱吞吐量灰色GM(1,1)预测值为：

(1)

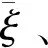
根据C和P的大小将模型的精度划分为四种等级，当所有指标均满足时，方可划分进该等级，详见表1[6]。

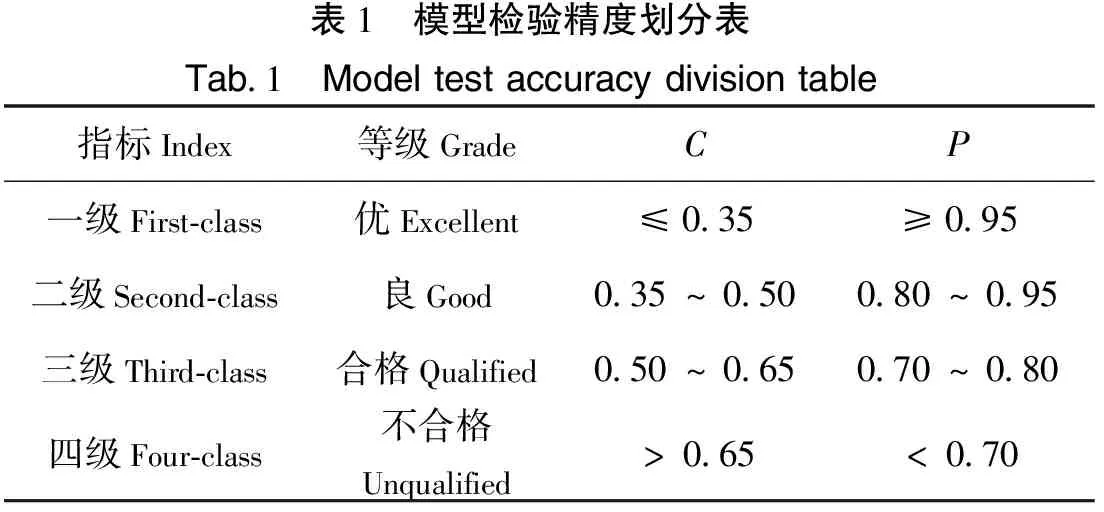
表1 模型检验精度划分表Tab.1 Model test accuracy division table指标Index等级GradeCP一级First-class优Excellent≤0.35≥0.95二级Second-class良Good0.35～0.500.80～0.95三级Third-class合格Qualified0.50～0.650.70～0.80四级Four-class不合格Unqualified>0.65<0.70

1.2 新陈代谢灰色GM(1,1)模型

进行港口集装箱吞吐量预测时，一般采用静态数据进行建模预测。预测得到的新数据如果能加入到原有数列的预测中，则能够降低预测误差。若数据能够新陈代谢，能够不断自我更新，则能够有效提高灰色GM(1,1)预测结果的精确性。

1.3 新陈代谢灰色GM(1,1)马尔科夫模型

为提高灰色GM(1,1)模型和新陈代谢灰色GM(1,1)模型的预测精度，运用马尔科夫模型分别对预测数据进行修正。具体计算流程如下：

1)划分状态区间

2)状态转移矩阵确定

3)预测值计算

2 芜湖港集装箱吞吐量预测应用

据芜湖市统计局数据，芜湖港2011—2020年集装箱吞吐量分别为22.05，25.03，28.77，40.26，50.15，60.21，70.40，80.30，100.63，110.26万TUE。本文以此为原始数列，分别构建模型进行集装箱吞吐量预测。

2.1 芜湖港集装箱吞吐量灰色GM(1,1)模型预测

将预测得到的结果，做累减计算，可得到芜湖港2014—2020年的集装箱吞吐量预测值。

2.2 芜湖港集装箱吞吐量新陈代谢灰色GM(1,1)模型预测

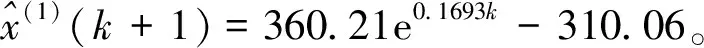
两个模型的芜湖港集装箱吞吐量预测结果如图1所示。通过计算，得到灰色GM(1,1)模型的后验差比值C=0.115，小误差概率P=1；新陈代谢灰色GM(1,1)模型的后验差比值C=0.118，小误差概率P=1。查表1可知,两模型的预测精度均达到优，说明模型预测结果较好。灰色GM(1,1)模型和新陈代谢灰色GM(1,1)模型的平均相对误差分别为0.021和0.020，需要对模型进一步修正，以提高预测模型的精确度。

2.3 两种模型马尔科夫修正预测

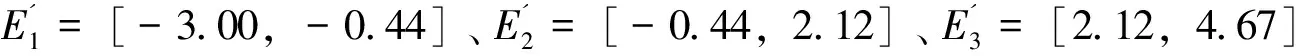
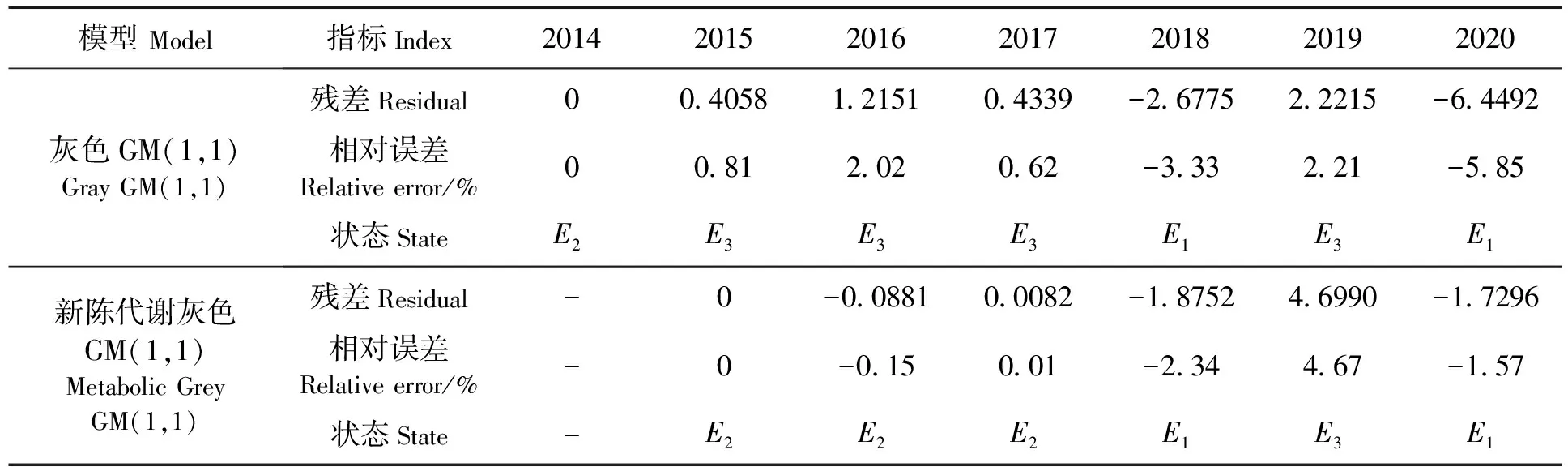
表2 两种模型相对误差分布及状态划分情况Tab.2 The relative error distribution and state division of the two models

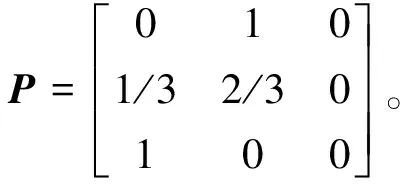
根据状态转移概率矩阵，依据概率最大原则，可对未来的状态做出相对可靠的预测。根据数据所处的状态，当误差大于1%时[9]，需要对预测的结果进行修正，否则不需要修正。对两个模型预测结果需要修正的数据进行修正，得到的结果如表3所示，与实际值对比情况如图2所示。

表3 两种模型马尔科夫修正结果Tab.3 Markov correction results for two models

再根据文献[5]中的公式，计算得到灰色GM(1,1)马尔科夫模型的C=0.080，P=1；新陈代谢灰色GM(1,1)马尔科夫模型的C=0.064，P=1。查表1可知,这两模型的预测精度仍处于优级。灰色GM(1,1)模型的平均相对误差和新陈代谢灰色GM(1,1)模型的平均相对误差分别为0.012和0.011。两预测模型的平均相对误差分别降低了43%和45%。可见灰色GM(1,1)马尔科夫模型和新陈代谢灰色GM(1,1)马尔科夫模型，相对于传统的灰色GM(1,1)模型和新陈代谢灰色GM(1,1)模型具有更高的精确度，且新陈代谢灰色GM(1,1)马尔科夫模型精确度更高。新陈代谢灰色GM(1,1)模型与新陈代谢灰色GM(1,1)马尔科夫模型的预测结果与实际结果的对比情况如图3所示。

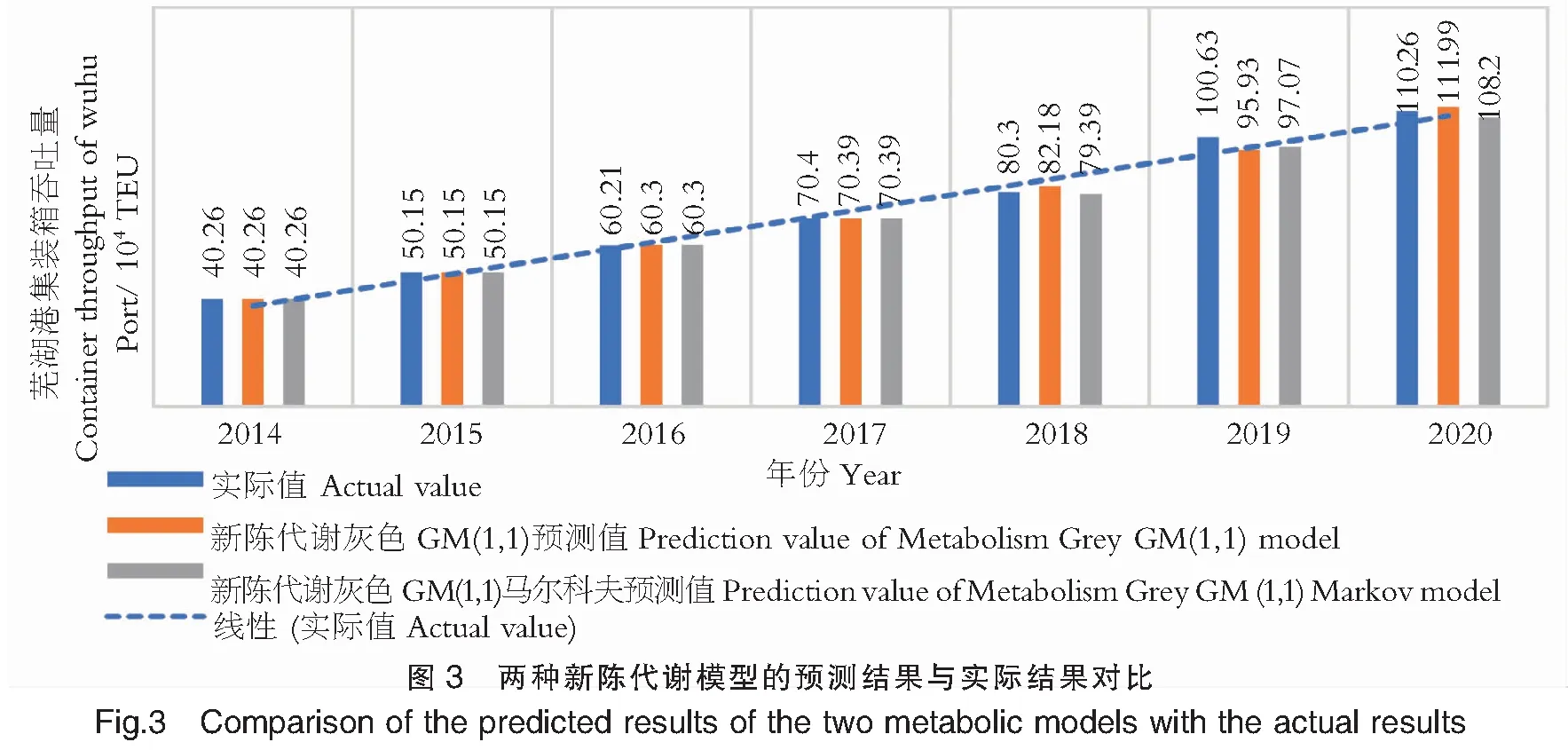
2.4 芜湖港集装箱吞吐量预测

3 结论

本文提出一种新陈代谢灰色GM(1,1)马尔科夫内河港口集装箱吞吐量的预测方法。用安徽芜湖港近年集装箱吞吐量数据，分层递进构建了灰色GM(1,1)模型、新陈代谢灰色GM(1,1)模型和灰色GM(1,1)马尔科夫模型、新陈代谢灰色GM(1,1)马尔科夫模型，再用这四个模型进行港口集装箱吞吐量预测。四模型预测结果中，灰色GM(1,1)马尔科夫模型比灰色GM(1,1)模型平均相对误差降低了43%，新陈代谢灰色GM(1,1)马尔科夫模型比新陈代谢灰色GM(1,1)模型平均相对误差降低了45%，由此得出新陈代谢灰色GM(1,1)马尔科夫模型的结果具有更高的可信度，可运用于预测内河港口集装箱吞吐量的结论。本研究为提高内河港口集装箱吞吐量预测的准确性，提高内河港口规划的合理性提供了一定参考。虽然预测精度有了一定的提高，但港口集装箱吞吐量受多方面因素的影响，如何将多影响因素结合到预测模型中，将是下一步的研究方向。