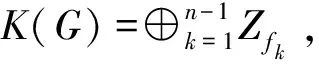完全分裂图的临界理想
李晓琳,王洪波,陈海燕
(集美大学理学院,福建 厦门 361021)
0 引言
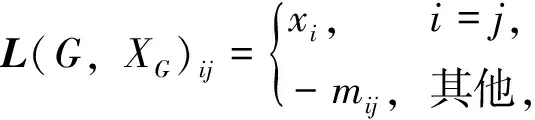
Ik(G,XG)=({detM|M为L(G,XG)的k-阶子矩阵})⊂Z[XG],
(1)
其中Z[XG]表示整数环上的多项式环,即一个图G的k-阶临界理想就是由它的广义拉普拉斯矩阵的所有k-阶子式生成的理想。平凡理想记为式(1)。
临界理想作为图临界群的推广是由文献[1]首先提出的,它也被看作是图的邻接特征多项式和拉普拉斯特征多项式的推广。随后人们发现,临界理想与图G的其他很多性质密切相关,如零迫数、团数等[2-4]。众所周知,确定一类图临界群的结构是比较困难的,作为临界群的推广,确定图的临界理想显得更为困难。到目前为止,只有完全图、路、圈、树、完全多部图等几类非常特殊图类的临界理想得到了研究[1,5-6],研究的方法基本上是组合方法。本文将利用线性代数的方法研究完全分裂图的临界理想。下面首先给出它的定义。

文献[7]研究了完全分裂图上沙堆模型的所有常返构型和其他各种组合对象之间的关系。本文首先用代数方法得到完全分裂图临界理想的一个具体表达式,然后应用此表达式完全确定了其临界群的结构。
1 完全分裂图的临界理想
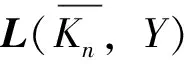
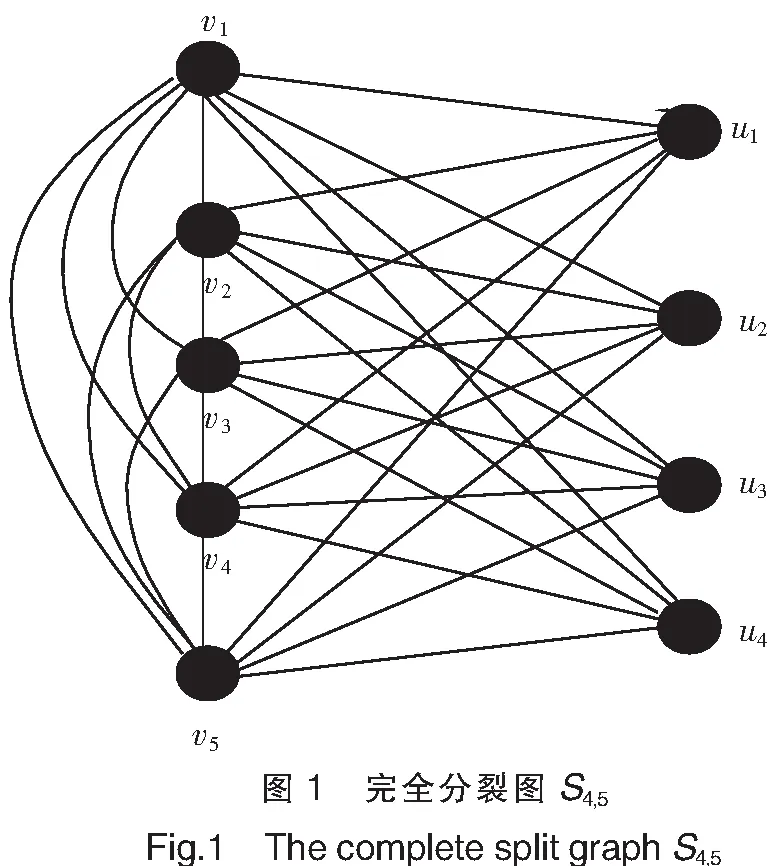
设M是L(Sn,m;Y,X)的任意一个k-阶子矩阵(1≤k≤n+m)。令R=R1∪R2、C=C1∪C2分别表示它的行指标和列指标集,其中,R1=R∩U,C1=C∩U,R2=R∩V,C2=C∩V。首先注意到,当|RiCi|≥2(i=1,2)时,M中至少有两行元素相同,所以det(M)=0。因此,计算完全分裂图Sn,m的k-临界理想Ik(Sn,m;Y,X)=({detM|M为L(Sn,m;Y,X)的k-阶子矩阵})=({detM≠0|M为L(Sn,m;Y,X)的k-阶子矩阵}),只需考虑|RiCi|≤1、|CiRi|≤1(i=1,2)的情形。为清楚起见,令ri=|Ri|,ci=|Ci|,i=1,2,则M有如下的分块形式:
(2)
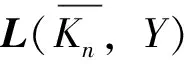
注意到,式(2)中r1+r2=c1+c2=k且|ri-ci|≤1,i=1,2。所以只有3种可能:1)r1=c1(r2=c2);2)r1=c1+1(r2=c2-1);3)r1=c1-1(r2=c2+1)。
为简单起见,下面省略矩阵的下标,令j=(1,1,…,1)表示全1行向量,jT表示它的转置,则对矩阵M,有如下结论。
引理1[2]设M是式(2)中的矩阵,则
为了给出det(M)的具体表达式,根据指标集Ri、Ci的选取,把P(Q)分为4类:1)类型b,R1=C1(R2=C2),对应的矩阵记作Pb(Qb);2)类型u,|R1C1|=|C1R1|=1(|R2C2|=|C2R2|=1),对应的矩阵记作Pu(Qu);3)类型r,C1⊂R1,|R1C1|=1(C2⊂R2,|R2C2|=1),对应的矩阵记作Pr(Qr);4)类型c,R1⊂C1,|C1R1|=1(R2⊂C2,|C2R2|=1),对应的矩阵记作Pc(Qc)。
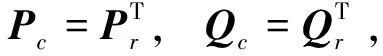
(3)
(4)
(5)

(6)
(7)
所以,
(8)
(9)

(10)
(11)
(12)
(13)
设M是式(2)中的矩阵,则根据其中P、Q类型,M可分为(b,b),(b,u),(u,b),(u,u),(r,c)((c,r))。
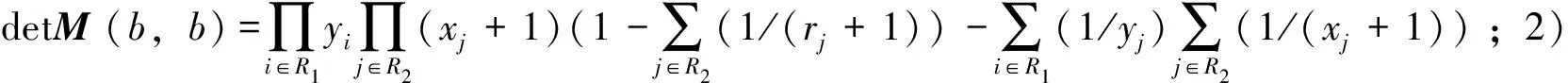
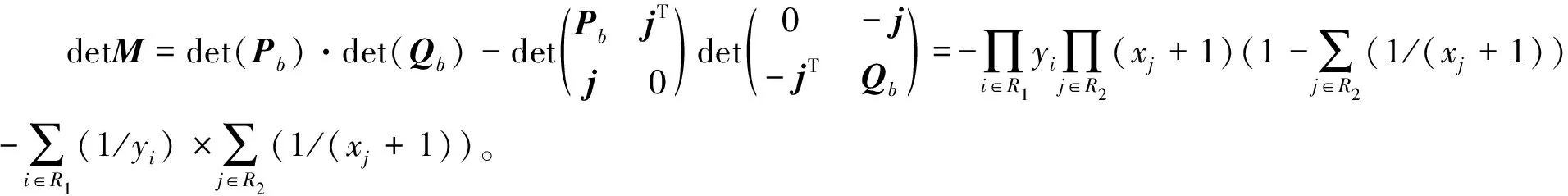
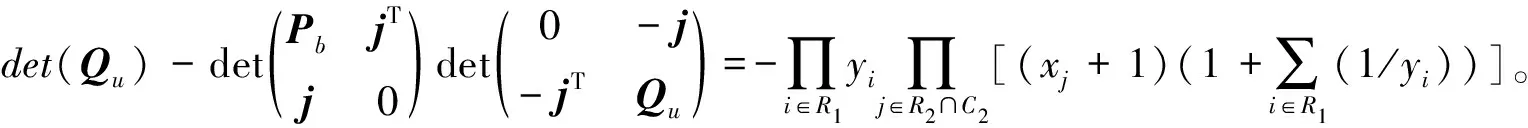
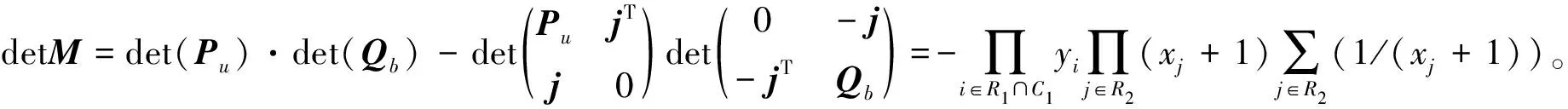
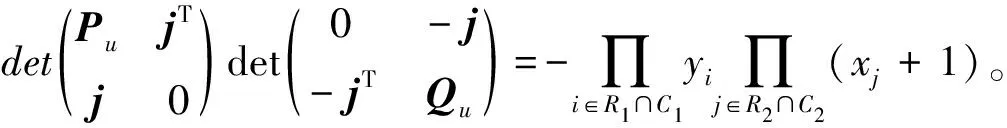
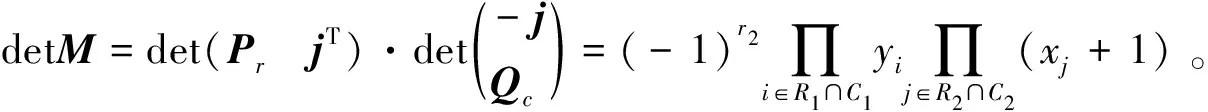
为了方便叙述,引进下面的记号。对任意的整数k,定义集合Ty,k={yi1,yi2,…,yik,0 为简单起见,下面用一些关于T和H代数表达式。两个集合的乘积是指它们指标集的卡氏积,而集合相加是指具有相同指标集的两两相加。 下面给出本文的主要结果。 定理1 对完全分裂图Sn,m(n,m≥2),其k-阶临界理想为 下面考虑3≤k≤n+m-1的情形。首先指出下面的事实,对任意的s≤s′,t≤t′,有 (14) 1)当3≤k≤n+m-2时,令M(u,u)表示L(Sn,m;Y,X)所有k-阶(u,u)型子式构成集合,则由引理2得,M(u,u)={Ty,sTx,t,s+t=k-2,s≤n-2,t≤m-2}。同理可得,M(b,b)={Ty,sTx,t-(Ty,s+Hy,s)Hx,t,s+t=k,s≤n,t≤m};M(b,u)={(Ty,s+Hy,s)Tx,t,s+t=k-1,s≤n,t≤m-2};M(u,b)={Ty,sHx,t,s+t=k-1,s≤n-2,t≤m};M(r,c)=M(c,r)={Ty,sTx,t,s+t=k-1,s≤n-1,t≤m-1}。由式(14)得,M(b,b)和M(r,c)中的每一个元素都可由M(u,u)中的元素生成,而M(b,u)中除了(Ty,n+Hy,n)Tx,k-n-1,M(u,b)中除了Ty,k-m-1Hx,m,其他元素都可由M(u,u)中的元素生成,所以,Ik(Sn,m;Y,X)=(Ty,sTx,t,s+t=k-2,s≤n-2,t≤m-2;(Ty,n+Hy,n)Tx,k-n-1,Ty,k-m-1Hx,m)。 2)当k=n+m-1时,此时M(u,u)=Ø,M(b,b)={Ty,nTx,m-1-(Ty,n+Hy,n)Hx,m-1,Ty,n-1Tx,m-(Ty,n-1+Hy,n-1)Hx,m};M(b,u)={(Ty,n+Hy,n)Tx,m-2};M(u,b)={Ty,n-2Hx,m};M(r,c)=M(c,r)={Ty,n-1Tx,m-1}。同样由式(14)得,In+m-1(Sn,m;Y,X)=(Ty,n-1Tx,m-1,Ty,n-2Hx,m,(Ty,n+Hy,n)Tx,m-2)。 首先给出临界群的定义,详见文献[8]。设G是一个n个顶点的连通图,L(G)=L(G,XG)|XG=D是它的拉普拉斯矩阵,这里D={d1,d2,…,dn}是图G的顶点度集合。令 fk=Δk/Δk-1,k=1,2,…,n, (15) 定理2 对完全分裂图Sn,m(n,m≥2),则 其中a=gcd(n,m)。 证明由完全分裂图Sn,m的定义,它的度集合D={m,…,m;m+n-1,…,m+n-1},所以,Ty,s|D={ms},Tx,s|D={(m+n)s},Hy,s|D={sms-1},Hx,s|D={s(m+n)s-1}。 由定理1可得Δ1=Δ2=1,Δn+m-1=mn-1(n+m)m-1。对3≤k≤n+m-2,不妨设n≥m,计算可得Δk, 由式(15)可得,f3=f4=…=fm=gcd(m,n+m)=a,fm+1=…=fn=m,fn+1=…=fn+m-2=m(n+m)/gcd(m,n+m)=m(n+m)/a,fn+m-1=m(n+m)。结果得证。同理可证m>n的情况。 令μ(G)表示临界群K(G)最小生成元的个数,则由定理2可得下面的推论1。 推论1 对完全分裂图Sn,m(n,m≥2),则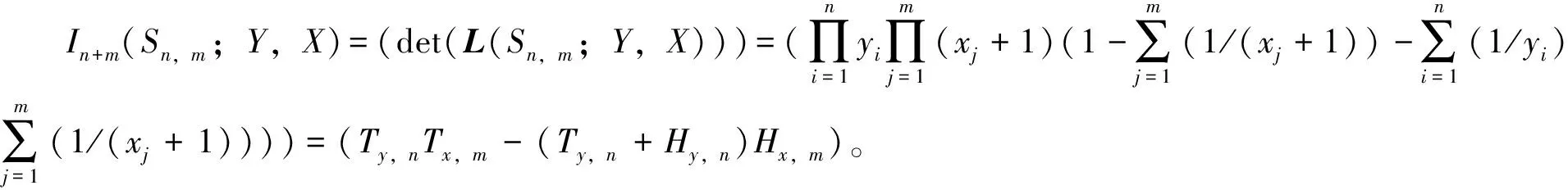
2 完全分裂图的临界群