单位圆盘外单叶调和映射的面积定理

石擎天,林珍连

(1.泉州师范学院数学与计算机科学学院,福建 泉州 362000；2.华侨大学数学科学学院,福建 泉州 362021)

0 引言

设Δ={z:|z|<1}是复平面C上单位圆盘，Δ*=C/Δ是单位圆盘外区域。记Σ为Δ*到C上共形映照f(满足规范化条件f′(∞)=1和f(∞)=∞)的全体，即f∈Σ可表示为

(1)

20世纪80年代以来,Σ类函数的面积估计、拟共形延拓、像域特征的刻画等问题得到深入研究[1-2]。记Σ′={f∈Σ:f(z)≠0}，Σ′类函数可与S类建立一一对应关系,即f∈S当且仅当g∈Σ′,其中g(z)=1/f(1/z)。1914年，为了证明S类中系数估计|a2|≤2，Gronwall[3]借助S类与Σ类间这种紧密联系，运用Parseval公式得到经典的面积定理,即定理1。

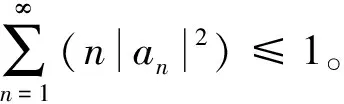
1971年，Lehto[4]推广了定理1，即定理2。

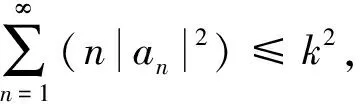
(2)

其中a1是复常数,且|a1|<1。

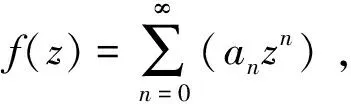
Dirichlet积分是研究拟共形映射极值性和调和映射存在性的重要工具[5-6]。受定理1和定理2的启发，本文将Σ类推广到调和映射中。

设ΣH是Δ*上单叶保向调和映射全体，且满足规范化条件为

(3)

拟共形映射是复分析中非常重要的研究对象，是共形映射的推广，且与调和映射既有紧密联系又有较大差异,因此，它吸引了广大学者们进行深入研究[8-11]。ΣH类是调和映射理论研究中非常重要的函数类，其面积偏差、单叶半径、星象与凸像特征刻画、Lipschitz连续性等问题的研究备受关注，并得到了一些较好的结果[7，12-16]。

本文在定理1和定理2的研究方法基础上，结合ΣH类函数的性质，对相应面积定理进行分析，结果推广了定理1和定理2，为深入研究ΣH类的系数估计、Lipschitz连续性、拟共形性等提供了一定的理论参考。

1 主要结果及其证明

为了给出具有拟共形延拓性的单叶调和映射的系数估计，先分析ΣH类的面积估计。

引理1 若f∈ΣH，则

(4)

证明设E是复平面C中紧致连通集使得ω=f(z)在Δ*上的函数值不取E中的点，即f(Δ*)∈CE。对于r>1，设Cr是f在圆周|z|=r上的像。因为f是单叶的，所以Cr是一条简单闭曲线，且其围成的闭域Er⊃E。由Green定理可得Er的面积为

(5)

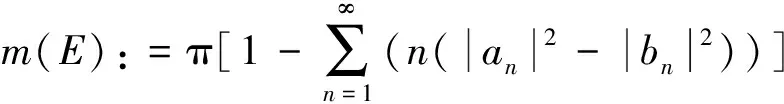
注1 由引理1的证明可知，式(4)中等号成立当且仅当f∈∑H且m(E)=0。特别地，当A=0且bn=0对所有n=1,2,…时，引理1恰为定理1。因此，引理1是共形映射f∈Σ的面积定理的推广。

应用上述面积定理,得到了具有拟共形延拓性的单叶调和映射的系数估计如下。

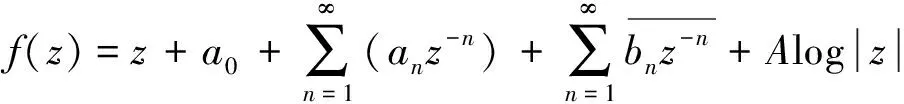
(6)

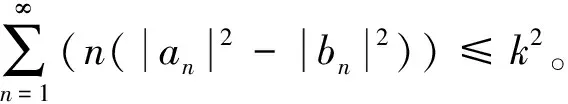
(7)

其中，a0,a1是复常数且|a1|=k<1。

证明证明过程可分A=0和A≠0两种情况。

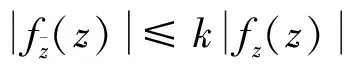
(8)

另外，对于ρ>1，对f运用Cauchy-Green公式可得，

当|ξ|=ρ→∞时，则有

(9)

(10)

将式(8)代入式(10)可得

(11)

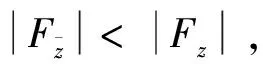
接下来将证明F(z)在Δ*上单叶，即对Δ*内任意两点z1,z2且z1≠z2，验证F(z1)≠F(z2)。当|z1|=|z2|时，F(z1)-F(z2)=f(z1)-f(z2)≠0，从而F(z)在Δ*上单叶；当|z1|≠|z2|时，不妨设argz1=argz2且|z1|<|z2|(否则,若argz1≠argz2，则考虑用eiθz1代替z1,使之满足arg eiθz1=argz2，其中θ是某个常数)。由于

其中γ是Δ*内连接z1,z2的可求长曲线，所以F(z)也在Δ*上单叶。令

其中f*是f在Δ上的拟共形延拓，则g可拟共形延拓到复平面C且复特征满足|ω(z)|≤k。基于A=0情形的证明可知,f的系数也满足式(11)。

最后说明等号取等的条件。若f定义如式(7)，则bn=0,n=1,2…且an=0,n=2,3…，此时f在Δ*内1-拟共形，在Δ内K-拟共形，这里,k=|a1|=(K-1)/(K+1)<1，即式(11)显然成立。

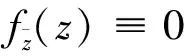
例1 函数f(z)=z+a1/z+Alg|z|，其中|a1|<1满足式(6)。

对所有z∈Δ*都成立。