与指数函数、对数函数有关的最值(值域)问题

宋月英

(甘肃省兰州市第十四中学)

本文拟通过归类举例的形式,具体说明如何准确求解以指数函数、对数函数为载体的最值(值域)问题,旨在帮助学生巩固所学知识,并灵活应用所学方法求解问题,进一步提高处理此类问题的能力,进而提升数学运算与逻辑推理等核心素养.

1 求函数的最值

例1已知函数y＝4－x＋21－x－5,当－1≤x≤0时,求该函数的最小值和最大值.

求解本题的关键在于通过换元变形将原问题转化为熟悉的一元二次函数在某区间上的最值问题,再借助“配方”变形即可顺利获解.

例2已知函数f(x)＝2－log3x(x∈[1,9]),且函数g(x)＝[f(x)]2＋f(x2),求函数g(x)的最小值和最大值.

注意到函数f(x)与f(x2)必须同时有意义,从而应满足解得x∈[1,3].因此,函数g(x)的定义域为[1,3].

因为g(x)＝[f(x)]2＋f(x2)＝(2－log3x)2＋2－log3x2＝(log3x)2－6log3x＋6,所以令t＝log3x,则由x∈[1,3],可得t∈[0,1],且

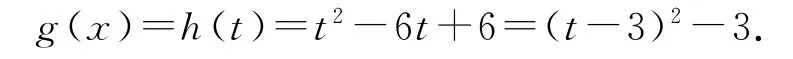
于是,当t＝1,即x＝3 时,g(x)取得最小值,gmin(x)＝1;当t＝0,即x＝1时,g(x)取得最大值,gmax(x)＝6.

求解本题需要关注两点:一是准确分析函数g(x)的定义域,要注意该函数的定义域并不是函数f(x)的定义域;二是在实施换元变形的基础上,需要等价转化目标问题.

2 求函数的值域

例3求下列函数的值域:

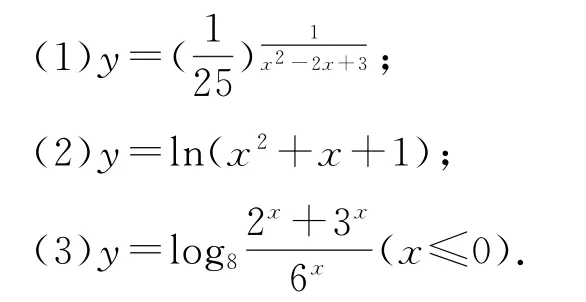
(1)因为x2－2x＋3＝(x－1)2＋2≥2,所以,所以根据指数函数在R上单调递减,可得

求解复合函数的值域时,需要先求出复合函数内层函数值的取值范围,然后灵活运用外层函数——指数函数(或对数函数)的单调性加以灵活分析.

3 由给定的最值，求参数的值

例4已知当x∈[1,3]时,函数y＝ax2－3x＋3(a＞0,a≠1)有最大值8,求实数a的值.

因为x2－3x＋3＝,所以当x∈[1,3]时,易知,从而可得

又因为底数a与1的大小关系不确定,所以需要进行分类讨论.

若a＞1,则ax2－3x＋3≤a3,所以根据已知条件“当x∈[1,3]时,函数有最大值8”可得a3＝8,解得a＝2(满足前提条件a＞1).

若0＜a＜1,则,所以根据已知条件“当x∈[1,3]时,函数有最大值8”可得,解得a＝16,这与前提条件0＜a＜1矛盾.

综上,实数a的值为2.

尽管本题给定函数的最大值,但是仍要按照求函数最大值的方式去思考.利用指数函数、对数函数的单调性解题时,如果不能确定底数a与1的大小关系,那么需要分两种情况(a＞1和0＜a＜1)进行讨论.

4 由给定的值域，求参数的取值范围

例5已知函数f(x)＝log2023[(a2－1)x2＋2(a＋1)x＋1]的值域为R,求实数a的取值范围.

要满足函数f(x)的值域为R,则应使g(x)＝(a2－1)x2＋2(a＋1)x＋1的函数值能够取遍所有的正数.

又因为a2－1与0的大小关系不确定,所以需要进行分类讨论.

当a＝1时,因为函数g(x)＝4x＋1,其函数值的值域为所有的正数(此时f(x)的定义域为＋∞)),所以a＝1满足题意.

当a＝－1时,因为g(x)＝1,其函数值不能够取遍所有的正数,所以a＝－1不满足题意.

当a≠±1时,因为g(x)是二次函数,所以由题意可知该二次函数的图像开口向上,且与x轴相切或相交.设方程g(x)＝0 的两个实数根为x1,x2,且x1≤x2,此时原函数的定义域为{x|x≤x1或x≥x2},因而可得不等式组

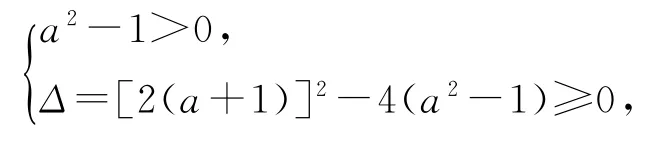
解得a＞1.

综上,实数a的取值范围为[1,＋∞).

1)本题易出现错解:根据函数f(x)的值域为R,先得到不等式(a2－1)x2＋2(a＋1)x＋1＞0恒成立,再据此进行分析.请思考:如此对函数的值域进行转化,为什么是不可行的.

2)如果对数型函数f(x)＝logm(ax2＋bx＋c)的值域是R,那么当a＝0 时,有b≠0;当a≠0 时,有

结合上述举例剖析可知:准确理解指数函数和对数函数的图像与性质,有助于顺利破解有关函数的最值(值域)问题.此外,解题时还需灵活应用等价转化思想、分类与整合思想以及二次函数的图像与性质等.

链接练习

1.定义max{a,b,c}为a,b,c中的最大值,设M＝max{2x,2x－3,6－x},则M的最小值是( ).

4.已知函数f(x)＝|log3x|,0＜m＜n,且f(m)＝f(n),若函数f(x)在[m2,n]上的最大值为2,则

链接练习参考答案

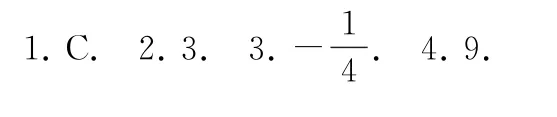
(完)