例谈指数型函数的参数取值范围问题
王丽馨
(黑龙江省大庆市第二十三中学)
求参数的取值范围问题通常已知一个变量的取值范围,要求另一个变量的取值范围,既是高考的热点问题,也是难点问题,对学生的能力要求较高,综合考查了学生的逻辑推理能力和运算求解能力,同时也考查了数学思想与数学方法.本文从指数型函数的参数取值范围问题入手进行研究,对解决此类问题的方法进行归纳总结,以期帮助学生快速突破此类问题.
1 数形结合
例1若a>0且a≠1,函数f(x)=x2-ax,当x∈(-1,1)时,均有则a的取值范围是( ).
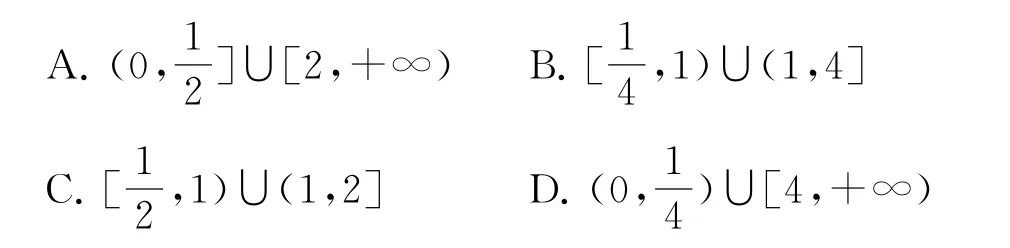
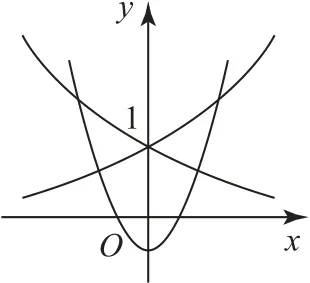
图1
综上,a的取值范围是,故选C.
对于不等式恒成立问题,可构建两个函数,利用函数图像比较两个函数的大小关系时,可先列出相应的不等式,再进行求解.
2 参变分离
例2若(m-m2)4x+2x+1>0在(-∞,-1]上恒成立,则实数m的取值范围是( ).

由(m-m2)4x+2x+1>0,得

对于给定的不等式恒成立问题,常通过恒等变换分离出参数进行求解,即若m≥f(x)恒成立,则m≥fmax(x);若m≤f(x)恒成立,则m≤fmin(x).
3 利用函数的单调性与奇偶性求解
例3设f(x)是定义在R上的偶函数,且当x≤0时,f(x)=2-x,若f(x)≥[f(x-m)]2在[m,m+1]恒成立,则正数m的取值范围为( ).

因为函数f(x)是定义在R 上的偶函数,且当x≤0 时,f(x)=2-x,则当x≥0 时,-x≤0,f(x)=f(-x)=2x,故对任意的x∈R,f(x)=2|x|.对任意的x∈[m,m+1],f(x)≥[f(x-m)]2恒成立,即2|x|≥22|x-m|,则|x|≥2|xm|对任意的x∈[m,m+1]恒成立,且m为正数,则x≥2(x-m),解得x≤2m,所以m+1≤2m,解得m≥1.故选A.
例4已知定义在R 上的函数f(x)=是奇函数.
(1)求n的值,并写出f(x)的单调递减区间(不必证明);
(2)若对任意的t∈[1,2],不等式f(t2)+f(ta+2a)≤0恒成立,求实数a的取值范围.
解析(1)因为f(x)是定义在R 上的奇函数,则,解得n=-1,此时f(x)=,经检验函数f(x)为奇函数,且

所以函数f(x)的单调递减区间为(-∞,+∞),无单调递增区间.
(2)因为f(t2)≤f(-ta-2a),且函数f(x)在R上单调递减,所以t2≥-ta-2a,即t2+ta+2a≥0,令g(t)=t2+at+2a,该函数的图像开口向上,对称轴为直线

点评根据函数的奇偶性,对不等式进行参变分离得出关于变量的不等式,进而求解.也可以将所求问题转化为函数的最值问题,转化方式如下:若f(x)≤0恒成立,则fmax(x)≤0;若f(x)≥0恒成立,则fmin≥0.
4 双变量问题转化为函数的最值问题求解
例5已知函数,g(x)=2x+a,若,∃x2∈[2,3],使 得f(x1)≥g(x2),则实数a的取值范围是( ).


例6已知函数f(x)=x2,若∀x1∈[0,2],∃x2∈[-1,3],使得g(x1)=f(x2)成立,求实数m的取值范围.
当x∈[-1,3]时,fmin(x)=f(0)=0,fmax(x)=f(3)=9,所以当x∈[-1,3]时,函数f(x)的值域为[0,9].因为在区间[0,2]上单调递减,则gmax(x)=g(0)=1-m,由题意可知,函数g(x)在[0,2]的值域是函数f(x)在区间[-1,3]上的值域的子集,所以解得-8≤m≤.
对于不等式恒成立问题,解题关键是转化为求函数的最值,转化时要注意全称量词与存在量词对题意的影响,可按如下规则等价转化.
一般地,已知函数y=f(x),x∈[a,b],y=g(x),x∈[c,d].
1)若∀x1∈[a,b],∀x2∈[c,d],有f(x1)<g(x2)成立,故fmax(x)<gmin(x);
2)若∀x1∈[a,b],∃x2∈[c,d],有f(x1)<g(x2)成立,故fmax(x)<gmax(x);
3)若∃x1∈[a,b],∃x2∈[c,d],有f(x1)<g(x2)成立,故fmin(x)<gmax(x);
4)若∃x1∈[a,b],∀x2∈[c,d],有f(x1)<g(x2)成立,故fmin(x)<gmin(x);
5)若∀x1∈[a,b],∃x2∈[c,d],有f(x1)=g(x2)成立,则f(x)的值域是g(x)值域的子集.
(完)

