基于抗差估计和改进AIME的缓变故障检测方法

姜颖颖, 潘树国, 叶 飞, 高 旺, 马 春, 王 浩

(东南大学仪器科学与工程学院, 江苏 南京 210096)

0 引 言

全球导航卫星系统(global navigation satellite systems, GNSS)/惯性导航系统(inertial navigation system, INS)组合导航因其精度较高、可靠性好及适应性强等特点,已在航空航天、铁路运输等诸多领域得到了广泛应用。然而,时钟漂移、卫星轨道建模和电离干扰等因素增大了组合导航中卫星的原始伪距观测量发生缓变故障的可能性。该类故障在发生时幅值较小且持续时间长,早期很难被察觉,从而严重影响系统的可靠性和稳定性。因此,研究如何及时、有效地检测缓变故障这一问题具有十分重要的现实意义。

目前用于组合导航卫星故障检测的方法主要有以下两类:“快照”法和“连续”法,其中“快照”检测法只利用当前历元信息,而“连续”法基于历史观测信息。典型的“快照”法包括残差卡方检测法(residual chi-square test method, RCTM)、多解分离法(multiple solution separation, MSS)等。其中,RCTM只对幅值较大的突变故障检测有效。MSS法可有效检测缓变故障,但是计算成本较高。而对于“连续”法,自主完好性监测外推法(autonomous integrity monitoring extrapolation, AIME)和最优故障检测法(optimal fault detection, OFD)是两种等效方法，且都能够适用于缓变故障检测的场景,但OFD工程实现复杂。另外,文献[13]指出，相比于其他故障检测方法,AIME更适合用于组合导航系统的缓变故障检测。然而,滤波器的故障跟踪作用会降低AIME算法对缓变故障检测的敏感性。为了解决该问题,文献[19]提出基于抗差扩展卡尔曼滤波(robust extended Kalman filter, REKF)的缓变故障检测法,实验表明该方法能够提高系统对缓变故障的检测能力。文献[20]利用标准化新息构造抗差增益阵，削弱了故障跟踪对缓变故障检测的不利影响。但是,上述抗差估计中的等效权函数大都是基于正态分布统计量构造的,并没有充分利用多余观测信息,因此在一定程度上限制了系统的抗差性能。本文将该类基于正态分布的REKF方法记为REKF-N。另外,传统AIME法利用卡尔曼滤波在外推过程中的新息序列构造缓变故障检测统计量。因此,在缓变故障结束后，系统会发生一段时间的虚警现象,从而导致定位结果精度下降。文献[22]基于层次滤波器设计了一种改进型AIME-RCTM的联合故障检测算法,通过判断RCTM检验统计量的状态是否满足上一时刻有故障而当前时刻无故障的条件，对缓变故障结束时刻进行判定。然而,在缓变故障结束前,RCTM检验统计量若没能超出检测门限,该判定方法则失效。

本文为解决由常规扩展卡尔曼滤波器(extended Kalman filter, EKF)的故障跟踪导致的缓变故障检测延迟问题,设计了一种改进的REKF。该方法利用当前历元下所有卫星观测值对应的新息构造服从标准分布的统计量,然后基于IGG-Ⅲ (Institute of Geo-desy & Geophysics Ⅲ)方案自适应卡尔曼增益阵,提升AIME算法对缓变故障检测的灵敏度。同时,为了应对AIME因累积作用导致系统在缓变故障结束后仍会出现虚警的问题,本文对常规AIME算法加以改进。结合AIME对系统状态的判定,定义了用作缓变故障结束时刻判定基本元素的统计量。然后，在AIME检测出系统存在缓变故障的情况下,利用样本分位数原理对序列进行异常值检验,从而判断缓变故障结束时刻。仿真结果证明了所提方法的有效性。

1 基于EKF的缓变故障检测法

1.1 GNSS/INS紧组合模型

GNSS/INS紧组合导航系统的状态分别由惯导系统和卫星系统两部分的误差状态组成。同时,GNSS的伪距和INS的观测量是组合系统的输入。滤波器中的状态向量共17维,具体定义为

(1)

EKF的状态方程和量测方程分别为

=(-1)-1+-1

(2)

=()+

(3)

式中:是状态向量;(-1)表示从历元-1到的状态转移矩阵;为观测向量;(·)表示状态和观测之间的非线性关系;是历元的过程噪声向量;为历元的观测噪声向量,其中,相互独立,且两者均服从零均值的高斯分布,协方差矩阵分别用和表示。

预测和更新是EKF算法的两个重要组成部分。

(1) 预测

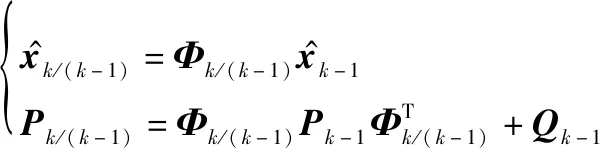
(4)

(2) 更新

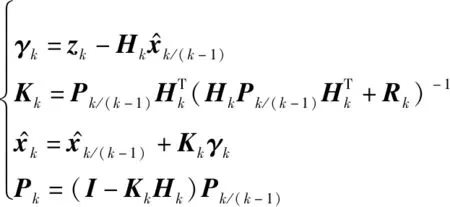
(5)

式中:符号“^”表示状态的估计;表示新息,是计算缓变故障检测统计量的基本元素;下标(-1)为从历元-1转移到;状态估计的误差协方差矩阵用表示;是卡尔曼增益矩阵;表示非线性矢量函数(·)的雅克比矩阵。

另外,新息的协方差矩阵用符号表示:

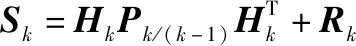
(6)

1.2 自主完好性检测外推法

在EKF中,由于新息包含了量测的全部信息,并且对异常的观测值极为敏感,因此新息是进行缓变故障检测的重要元素。AIME的主要思想就是利用卡尔曼滤波在外推过程中的新息序列构造故障检测统计量,然后基于假设检验原理判断系统是否存在缓变故障。

外推法的故障检测统计量为

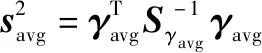
(7)

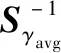
(8)

平均新息的表达式为

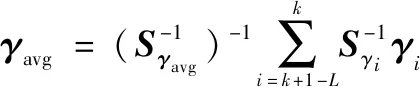
(9)

式中:表示新息序列的窗口长度。新息外推法就是利用多个历元(历元+1-到当前历元)新息序列的加权累加以提高对缓变故障的检测能力。

由假设检验理论可知:

其中,是自由度为的卡方分布非中心参数,表示可视星的数量;Th为故障检测的门限值:

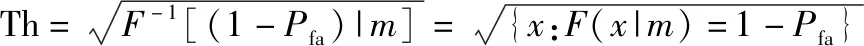
(10)

式中:表示故障检测的误警概率;(|)表示自由度为的中心卡方分布累积分布函数。误警率的确定与应用场景相关,本文取误警率=8×10。由式(10)可知,门限值仅取决于卡方分布的自由度和系统设定的误警率。

2 基于REKF的缓变故障检测法

2.1 基于标准t分布的REKF

当组合导航中的卫星伪距发生缓变故障时,EKF的故障跟踪现象会导致作为缓变故障检测重要元素的新息无法如实地跟踪到故障幅值的变化情况,从而延长外推法对缓变故障的检测延迟时间。而REKF能够通过自适应增益阵减弱发生缓变故障的观测值对状态估计的影响,这有利于对缓变故障进行及时检测。本文提出基于标准分布的REKF算法,并将其记为REKF-。该方法设计的大致思路为:利用当前历元下所有卫星观测值对应的新息构造服从标准分布统计量,然后基于IGG-Ⅲ方案自适应卡尔曼增益阵。由于在卡尔曼滤波更新过程中可以直接获得新息,因此基于新息计算等价权矩阵相比传统抗差阵的构造更为直接,简化了计算过程。另外,分布统计量的设计充分利用多余观测信息并引入自由度指标适时调整临界值,因此系统的抗差性能得以提升。

REKF与 EKF的最大区别在于滤波增益矩阵的构造。REKF-算法中的抗差增益阵为

(11)

(12)

式中:临界值,分别取(-2)分布显著性水平为,的分位数;是观测值对应新息的标准化分布统计量,可通过当前历元的新息向量和其对应的协方差矩阵计算:

(13)

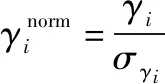
(14)

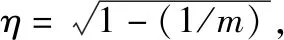
2.2 改进的AIME算法

由于传统外推法利用多历元观测信息累积检测缓变故障,因此在缓变故障结束后，系统会发生一段时间的虚警现象,影响定位结果精度。基于此,本文提出一种基于样本分位数的改进AIME算法。在对AIME和RCTM故障检测法进行理论分析的基础上,将两者故障检测统计量的比率定义为新的统计量,并将其用作缓变故障结束判定的基本元素,利用样本分位数原理对序列进行异常值检测,从而判定缓变故障的结束时刻。

2.2.1统计量的定义

当EKF收敛到一个相对稳定的状态,在给定时间窗口内,新息的协方差矩阵可视为不变的常矩阵。基于此,在历元下,AIME算法便转化为以下形式:

(15)

(16)

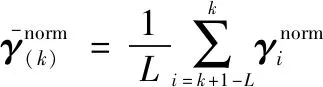
(17)

相应RCTM的单历元卡方统计量为

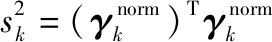
(18)

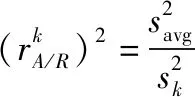
(19)

结合缓变故障的特点,即随着时间的推移,故障的幅值越来越大,其变化为一个随着时间累积的慢变增加过程。根据式(19),在故障的缓慢变化过程中,值应在一个固定的范围内波动。然而,当缓变故障结束时,由于AIME法的累积效应,此时的故障检测统计量通常无法快速降低到门限以下,不会发生显著变化。同时,由于RCTM统计量的计算仅依赖于当前历元的观测信息,所以该统计值在此时会迅速减小至系统未发生故障时的范围。RCTM中卡方统计值的变化导致值发生较大抖动,破坏了序列相对稳定的状态。由以上分析可知,序列出现异常值的时刻即对应缓变故障的结束时刻。结合AIME对系统状态的判定结果,本文将统计量具体定义为一个分段形式。

在历元,统计量可用下式计算:

(20)

222 样本分位数原理和缓变故障结束时刻的判定

样本分位数法是进行异常值检测最常用的方法之一。样本分位数是指针对没有分布先验信息的总体数据,在给定的概率(0<<1)下,若存在对应的,使(>)=,则为总体的上侧分位数。特别地,当=50%时,对应的样本分位数是样本中所有数据从小到大排列后的第50%的数值,即样本的中位数。

假设系统在历元检测到缓变故障,利用样本分位数原理判断缓变故障结束时刻(异常值检测)的步骤如下。

AIME算法检测到缓变故障后,计算后续各历元相应的值,生成数据样本:

(21)

设置时间序列窗口长度。的选取与所使用的样本分位数类型和AIME算法中的滑窗长度有关。过大的窗口可能会导致计算窗口内的样本分位数时对异常值发生漏检,窗口过小则丧失了统计样本分位数的意义。本文取窗口长度=3 s。

将序列转换为固定时间窗口的多个时间序列片段():

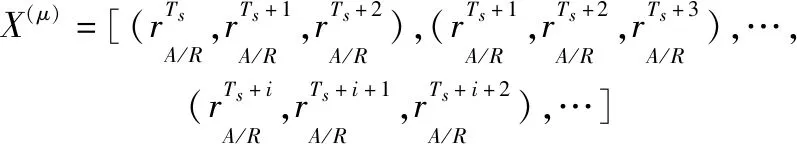
(22)

对每个时间序列片段进行样本分位数提取。结合统计量的特点,本文取=50%,即()中每个片段的中位数。由样本分位数组成的数据序列:

=[,+1,…,+,…]

(23)

将窗口内的数据与提取的样本分位数分别作差,得到序列Δ():

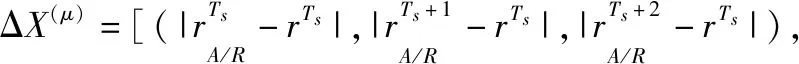
(24)

223 改进的AIME算法

(1) 算法的设计基于样本分位数统计方法;

(2) 数据样本()容量充足，是算法能够正常使用的前提;

(3) 样本稀疏可能导致算法的判定性能下降，甚至失效。

图1 基于REKF-t和改进AIME的缓变故障检测流程图Fig.1 Flowchart of detection of slowly growing fault based on REKF-t and improved AIME

3 仿真验证

3.1 实验数据与参数设置

为证明本文所提方法的有效性,利用仿真数据进行实验,验证本文所提方法对缓变故障的检测效果。在实验过程中,假设惯导正常工作,仅考虑卫星伪距发生缓变故障的情况。

系统仿真条件设置:在GNSS/INS紧组合导航系统中,假设陀螺随机常值漂移为[-0.000 9°/h;0.001 3°/h;0.000 8°/h],加速度计随机常值漂移为[30 μ;-45 μ;26 μ];GNSS伪距噪声为2.5 m,卫星可见数为8颗,编号分别为1～8,输出频率为1 Hz。飞机的飞行轨迹如图2所示。飞行历时418 s,其中包括两次45°的转弯和一次500 m的爬升。考虑到计算复杂性,取窗口长度=10 s。另取显著性水平=0.1,=0.01。

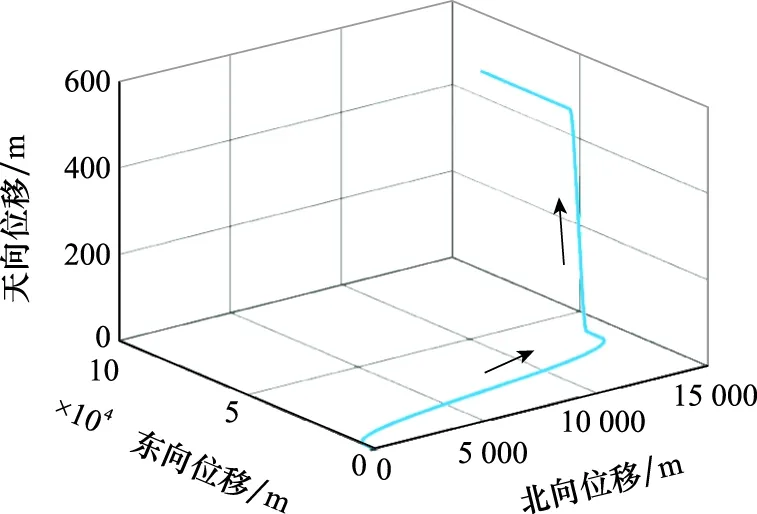
图2 飞机的仿真飞行轨迹Fig.2 Simulated trajectory of the aircraft

缓变故障的数学模型:

(25)

式中:表示缓变故障的速率;表示发生故障后卫星伪距观测值。

3.2 实验过程与结果分析

3.2.1 发生缓变故障的卫星新息

在151～299 s历元内向卫星1加入速率为0.15 m/s的缓变故障。图3给出由EKF和本文提出的REKF-两种滤波算法计算的卫星1新息值的变化情况。由图3可知,当系统存在故障时,EKF算法因受故障跟踪的影响,计算出的卫星1新息值低于理想的新息值。而在相同的故障场景下,REKF-算法能够明显改善故障跟踪的影响。仿真结果表明,在历元299 s利用REKF-计算的卫星1新息值可以达到22.5 m左右。因此,在缓变速率为0.15 m/s的故障场景下,使用REKF-算法能够使发生故障的卫星新息值反映出实际加入的缓变故障幅值。

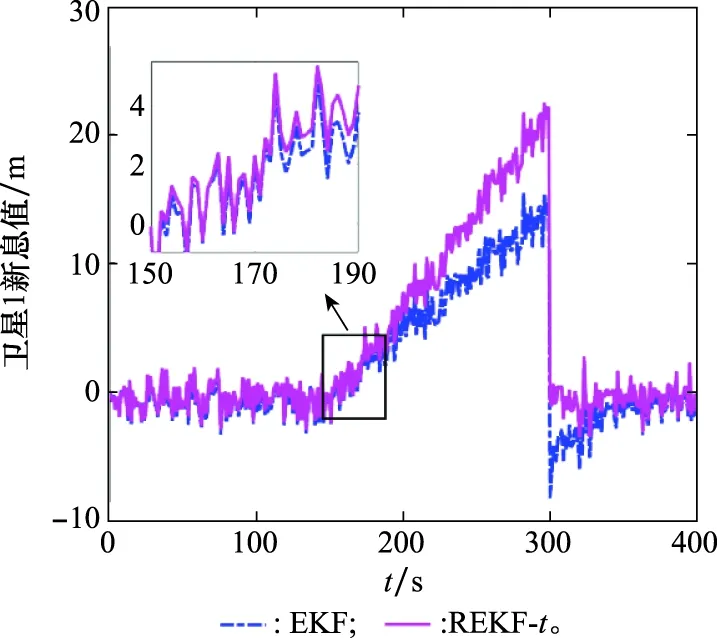
图3 卫星1在EKF和REKF-t下的新息值(0.15 m/s)Fig.3 Innovations of satellite 1 under EKF and REKF-t (0.15 m/s)

为验证本文所提算法对不同变化速率缓变故障的卫星新息值的校正效果,在151～299 s历元内向卫星1分别加入速率为0.1 m/s,0.15 m/s和0.25 m/s的缓变故障。图4给出不同缓变速率下基于REKF-计算的卫星1的新息值。仿真结果表明,在不同的缓变故障速率下,基于本文所提的REKF-算法都能够使得发生故障的卫星新息值跟踪到实际加入的缓变故障。

图4 卫星1在不同故障速率下的新息值(REKF-t)Fig.4 Innovations of satellite 1 at different fault rates (REKF-t)

3.2.2 缓变故障检测统计量

为了验证本文所提方法能够改善常规AIME算法的缓变故障检测延迟现象，在151～299 s历元内向卫星1加入速率为0.1 m/s的缓变故障。图5给出3种故障检测方案的变化曲线,Th为检测门限。当检测统计值超过门限,系统则被判定存在缓变故障。方案1为EKF联合常规AIME故障检测法;方案2为文献[20]中REKF-N联合常规AIME故障检测法;方案3为本文所设计的 REKF-联合改进AIME故障检测法，在图中分别用M1、M2和M3表示。由图5可知,方案3的故障检测方法最先检测出故障,方案1和方案2则滞后于该算法。同时,方案2先于方案1发现故障。仿真结果表明,对于发生在151～299 s历元内变化速率为0.1 m/s的缓变故障,3种方案分别在235 s、231 s和229 s检测到缓变故障。方案2与基于EKF的联合AIME算法相比,故障检测延迟时间缩短4 s,而方案3则提前6 s检测到缓变故障的存在。

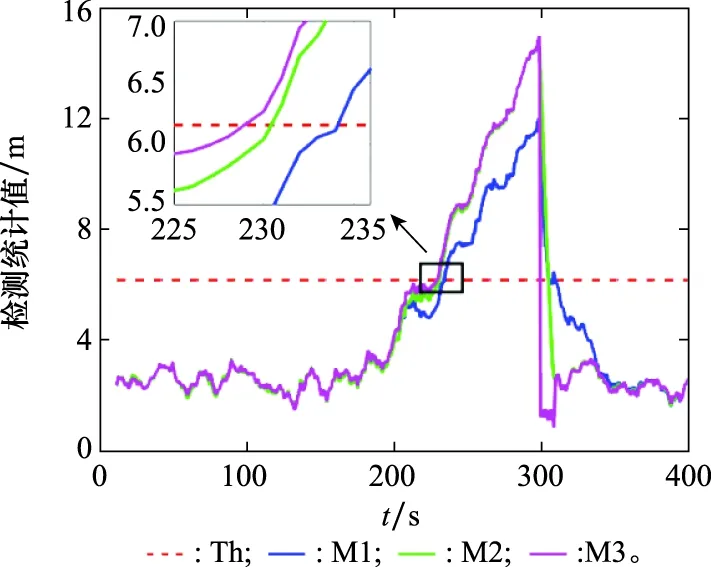
图5 故障速率为0.1 m/s的检测统计值的变化曲线Fig.5 Change curves of test statistics at 0.1 m/s fault rate

为了验证本文所提算法对缓变故障的检测效果,分别对不同变化速率的缓变故障进行了检测。图6给出缓变故障速率为0.15 m/s和0.25 m/s场景下3种方案对应的故障检测统计值,分别用虚线和实线表示两种速率的检测统计值变化。与检测缓变速率为0.1 m/s的故障场景结果相仿,方案3的故障检测统计值先于方案1和方案2超过门限,并且缓变速率越大,对应的检测统计值变化越快,系统越容易检测到缓变故障的存在。

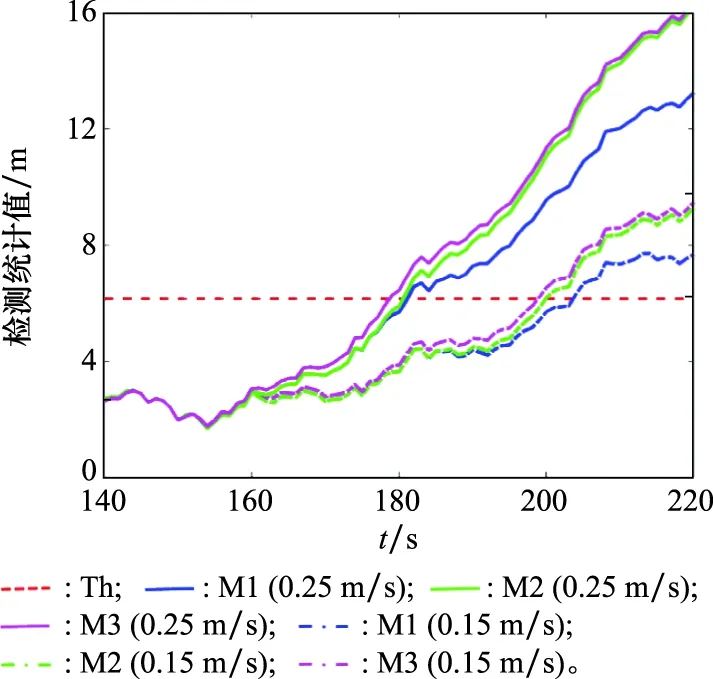
图6 故障速率0.15 m/s和0.25 m/s下检测统计值的变化曲线Fig.6 Change curves of test statistics at 0.15 m/s fault rate and 0.25 m/s fault rate

表1给出0.1 m/s,0.15 m/s和0.25 m/s 3种不同故障变化率下3种故障检测方案所对应的延迟时间的对比。由表1可以看出,缓变故障的变化速率越大,算法越容易检测出故障的存在,故障检测的延迟时间也就越短。在相同速率的缓变故障下,方案2和方案3先于方案1检测到故障,方案3提前于方案2发现缓变故障。另外,在3种缓变故障场景下,相较于方案1,方案2分别提前了4 s,3 s和1 s检测到缓变故障,而方案3则分别提前了6 s,5 s,3 s。通过比较可以发现,相较于速率相对大的缓变故障,使用方案3检测变化速率较小的缓变故障效果更优。但是，当缓变故障的速率相对较大时,方案3的检测性能却有所下降,但总是先于方案2检测到缓变故障。对于变化速率较大故障的及时检测，将在下一步研究工作中展开。

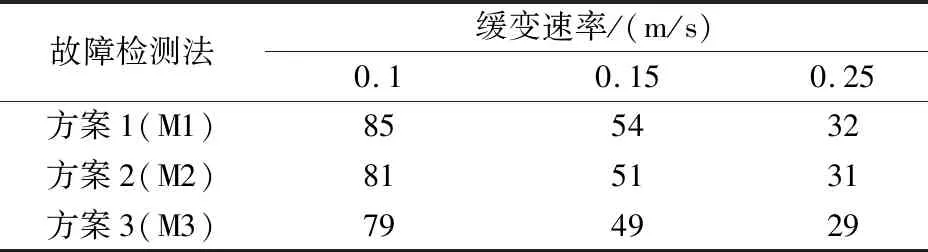
表1 3种检测方案延迟时间比较Table 1 Comparison of delay time under three fault detection schemes s

通过3种缓变故障场景的仿真实验分析可知,相较于EKF联合AIME和REKF-N联合AIME两种故障检测法,本文设计的故障检测方案对缓变故障更敏感,相应的故障检测延迟时间更短。由此证明,本文提出的方法对组合导航系统卫星缓变故障及时检测具备有效性。

3.2.3 缓变故障结束时刻的判定

为了证明改进的AIME法能够准确判定缓变故障的结束时刻,本文设计两类仿真场景进行相关实验。场景1:故障区间相同而变化速率不同;场景2:变化速率相同而故障区间不同。由于方案1(M1)和方案2(M2)都使用常规AIME算法,为了避免重复比较,在该部分仅对比分析M1和M3的结果。

(1) 场景1:同一故障区间,不同缓变速率

设置故障区间为151～299 s历元,缓变故障速率分别为0.1 m/s,0.15 m/s和0.25 m/s。本文以变化速率为0.15 m/s的缓变故障为例，分析基于样本分位数原理的改进AIME算法工作流程。整个飞行过程的序列如图7(a)所示。在AIME未检测到缓变故障前,系统的值始终为1。在199 s时,AIME算法检测到缓变故障的存在,此后的序列大致稳定在一个固定的范围,直至算法得到缓变故障的结束时刻。由此可证明在给定的时间窗口内,AIME与相应的RCTM统计量之间呈近似线性关系的结论。具体的理论分析可见第2.2节。由图7(a)可知,系统在199 s检测到缓变故障的存在,因此中位数提取将从历元201 s开始。各时间序列窗口内的50% 样本分位数提取曲线如图7(b)所示。仿真结果表明,中位数序列变化平稳,基本不受异常值的干扰。

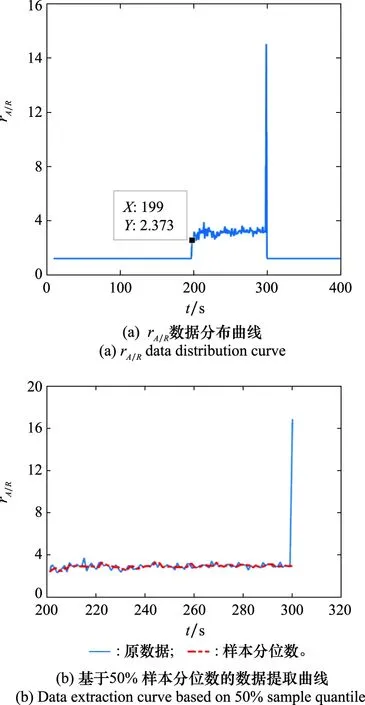
图7 0.15 m/s故障速率下改进AIME算法的工作流程Fig.7 Workflow of improved AIME algorithm at 0.15 m/s fault rate

将原始数据与图7(b)中的中位数序列作差,结果如图7(c)所示。当差值大于阈值时,则认为该数据为异常值,即可判定对应的历元为缓变故障结束时刻。图7(c)中,红色实线表示阈值,黑色虚线表示差值。由图7(c)可知,在历元199～299 s,黑色曲线始终处在红色阈值曲线之下;在历元300 s处,差值激增,迅速超出阈值。根据判别机制,300 s为缓变故障结束时刻。

按照同样的方法分别对速率为0.1 m/s和 0.25 m/s的缓变故障结束时刻进行判定。图8给出3种不同变化速率下故障检测统计值在故障结束时刻附近的变化曲线。由图8可以看出,缓变速率越大,基于常规AIME检测法导致系统发生虚警的现象越明显。仿真结果表明,改进的AIME算法在同一故障区间、不同变化速率的3种故障场景下均能够准确判定故障的结束时刻,并且在故障结束后的10个历元内使用RCTM故障检测机制,同时在第310 s历元后恢复AIME检测算法的使用。

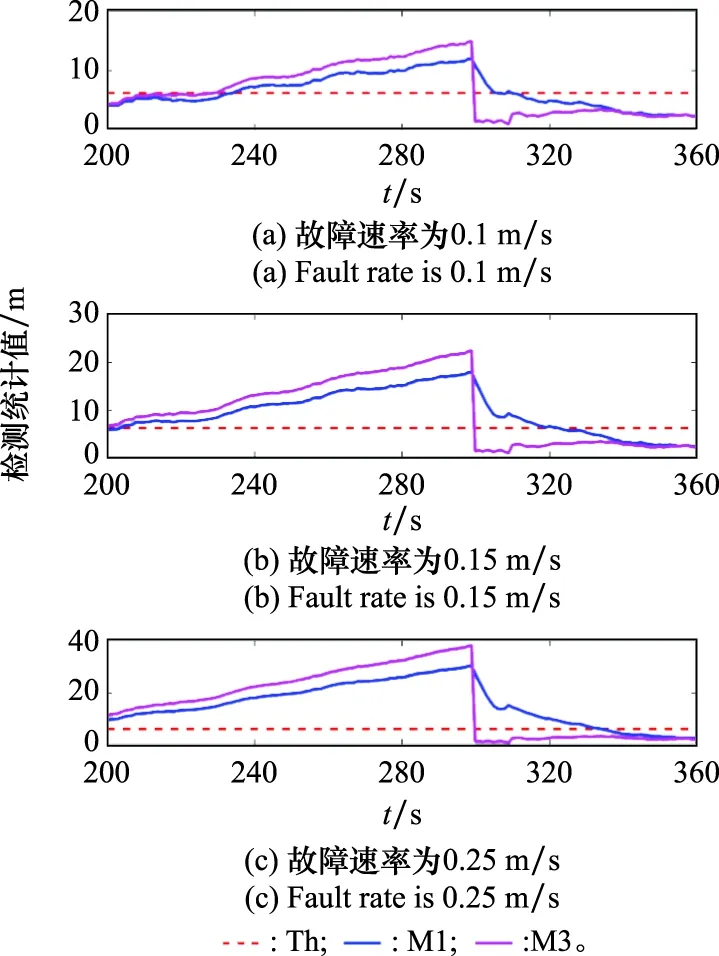
图8 两种故障检测方案在不同缓变速率下故障结束时刻对比图Fig.8 Comparison diagram of ending time of different fault rates under two fault detection schemes

(2) 场景2:同一缓变速率,不同故障区间

为了进一步分析改进AIME算法对缓变故障结束时刻的敏感性,以缓变速率为0.15 m/s的故障场景为例,将故障结束时刻分别设为250 s和280 s进行实验,相关参数设置不变。

图9 不同故障结束时刻的差值曲线Fig.9 Difference curves of different ending time of faults

图10 两种故障检测方案在0.15 m/s缓变速率下不同故障结束时刻对比图Fig.10 Comparison diagram of different ending time of 0.15 m/s fault rates under two fault detection schemes

通过分析利用样本分位数原理对缓变故障结束时刻的判定过程,以及比较相同故障区间不同变化速率以及相同变化速率不同故障区间两种情形的实验结果,可以得出:在数据样本充足的情况下,本文提出的改进方法对组合导航系统缓变故障结束时刻能够进行准确判定且缓变速率相同时,故障持续时间越长,判定性能越好。

4 结 论

(1) 本文提出的REKF-算法构造简单,临界值可变,能够有效缓解EKF的故障跟踪影响;

(2) 在相同的缓变故障场景下,相比于其他两种方案,基于REKF-的检测法能够率先觉察到故障的存在,可明显缩短检测延迟时间。实验结果表明,当缓变速率为0.1 m/s,0.15 m/s和0.25 m/s时,故障检测延迟时间分别缩短了6 s,5 s和3 s;

(3) 本文设计的改进AIME算法实现了对缓变故障结束时刻的正确判断,及时避免了传统AIME方法因累积效应而导致的虚警问题。