基扩展模型下基于LSTM神经网络的时变信道预测方法

聂 倩, 杨丽花, 呼 博, 任露露

(南京邮电大学江苏省无线通信重点实验室, 江苏 南京 210003)

0 引 言

近年来,随着通信技术的迅速发展,面向高速移动无线通信(如用于高速铁路、高速公路)的研究也越来越广泛。无线通信系统借助于准确的信道状态信息(channel state information,CSI),通过自适应地选择传输参数,可以获得较大的性能提升。现阶段,大多数无线通信系统通过信道估计来获取CSI。然而,在高速移动场景下,由于多普勒频移引起的信道快速变化将会导致信道估计获取的CSI出现老化现象,这将严重恶化高速移动通信系统的性能。信道预测由于可以提前预测未来的CSI,通过时间跨度来抵消延迟,能够有效地解决高速移动场景中CSI过时的问题,且无需消耗额外的无线电资源,因此信道预测被认为是高效获取高速移动场景CSI的有效途径之一。

现有的信道预测方法可以分为传统方法和基于深度学习的方法,传统方法通过将无线信道建模为一组无线电传播参数,并利用一阶自回归(autoregressive,AR)、线性最小均方误差(linear minimum mean square error,LMMSE)、支持向量机(support vector machine,SVM)等方法对传播参数进行预测,但在高速移动场景下,大的多普勒频移使得信道发生快速时变,这将导致信道具有非线性变化特性,利用传统线性估计方法(如一阶AR模型方法、LMMSE方法等)无法准确地捕获到信道的实际特征。此外,SVM方法需要将非线性预测问题映射到高维,这依赖于复杂的计算过程。因此,这些传统的估计方法在高速移动场景下的适用性受到了很大的限制。

与传统方法不同,基于深度学习的信道预测方法是依赖于数据的,其通过训练大量的数据自适应地捕获数据中固有的特征。其中,基于反向传播(back propagation,BP)神经网络,文献[7]通过对历史时刻的CSI进行线下训练和线上预测,来实现对未来时刻的CSI预测,但是由于BP神经网络属于前馈神经网络,未充分考虑预测序列在不同时刻的时间相关性,因此该预测模型不够精确。相比之下,由于循环神经网络,特别是长短期记忆(long short-term memory,LSTM)神经网络,可以有效地探索数据序列之间的时间相关性,因此目前许多研究人员使用LSTM神经网络进行信道预测。文献[8]和文献[9]分别给出了基于单层和双层LSTM神经网络的信道预测模型,通过将连续采样获得的信道响应送入LSTM神经网络,以实现时变信道的预测,但由于神经元数目较多,此方法的计算复杂度太大。文献[10]针对车对基础设施(vehicle-to-infrastructure,V2I)毫米波信道给出了一种包含卷积神经网络(convolutional neural networks,CNNs)、LSTM网络和全连接(fully connected,FC)层的盲CSI预测模型,该方法主要利用该模型来预测信噪比,并根据信噪比切换适当的调制模式,以提高通信质量。文献[11]针对智能互联汽车边缘计算网络给出了一种基于LSTM神经网络的预测方法,主要基于历史时刻和当前时刻的信道参数预测未来时刻的信道。与传统方法相比,深度学习方法能够更好地适配高速移动场景的信道条件,然而这些现有的方法在训练网络阶段通常将理想的、无噪声的信道参数作为逼近目标,这是与实际不符的,因为在实际的通信系统中,理想的信道信息是未知的。另外,现有的深度学习方法均直接利用历史CSI进行预测,导致预测过程中使用的参数过多,大大增加了计算复杂度。

为了解决以上问题,本文提出了一种基扩展模型(basis expansion model, BEM)下基于LSTM神经网络的时变信道预测方法。考虑到在高移动性场景中,不同车辆在同一位置处的无线信道具有很强的相关性,新方法首先借助历史时刻CSI的自相关矩阵求解最佳基函数,从而实现了对BEM的改进,然后利用基系数估计值预测信道系数,大大减少了预测的复杂度。在线下训练过程中,新方法将网络逼近的目标设置为基于较高精度的LMMSE方法估计的时域信道系数,而非理想的基系数,以增强预测模型的实用性。

1 系统模型

1.1 信号模型

本文考虑的是一个单入单出的正交频分复用(orthogonal frequency division multiplexing, OFDM)系统,假设是频域发送的第个OFDM符号,=[(0),(1),…,(-1)],其中()是第个OFDM符号第个子载波上的频域发送信号,是子载波的数目。在此,包含个导频符号与-个数据符号。

在接收端,接收到的第个频域OFDM符号为

=+

(1)

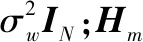
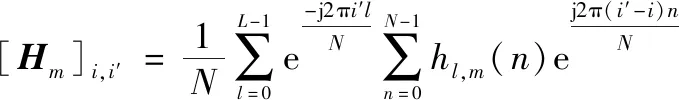
(2)

1.2 基于BEM的信道模型

BEM可以通过有限个基函数来模拟无线信道参数,采用BEM对信道建模可以减小计算复杂度。利用BEM,式(2)中的,()可以表示为

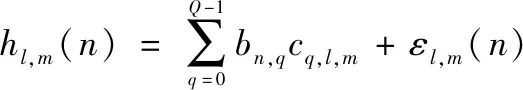
(3)

式中:,为第个基函数的第个组成分量,0≤≤-1,为使用的基函数的数目;,,为与第径第个OFDM符号周期上第个基函数对应的基系数;,()是采用BEM对信道建模时产生的建模误差。

将式(3)转化为向量形式,即

,=,+,

(4)

式中:,=[,(0),,(1),…,,(-1)];是×维的基函数矩阵,[],=,;

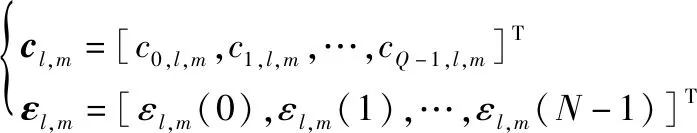
(5)

采用BEM对信道进行建模,则式(1)中的接收信号可以重新表示为

=+

(6)

式中:

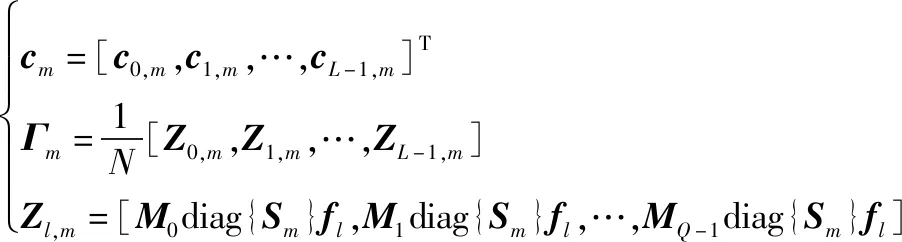
(7)

式中:是第个OFDM符号的基系数矩阵;是×维离散傅里叶变换矩阵的第列;是×维的矩阵,具体表示为

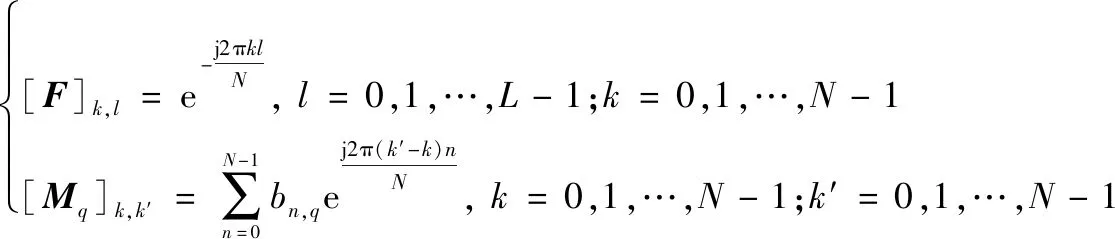
(8)

2 新方法

由于新方法是采用LSTM神经网络进行信道预测的,因此本节将首先对LSTM神经网络的基本原理进行扼要介绍,然后再对新方法进行详细介绍。

2.1 LSTM神经网络

与前馈神经网络相比,LSTM神经网络是一种典型的循环神经网络,该网络的每个LSTM单元都存在一个反馈回路,允许隐藏层内部的神经元自循环连接,能够充分预测序列的时间相关性,被广泛应用于信道预测领域。因此,新方法将采用LSTM神经网络进行信道预测。

图1展示了由一个输入层、两个隐藏层(即两个LSTM层)和一个输出层组成的深度LSTM网络,其中输入层、隐藏层、输出层的神经元节点数量分别为,,,,且每个隐藏层都会输出两种状态,即短期记忆单元和长期记忆单元。图1左侧给出了深度LSTM网络的简易结构,该图表示在任意时刻,将输入数据和前一时刻第一个LSTM层的输出送入到第一个LSTM层中,会生成一个中间向量,然后将和前一时刻第二个LSTM层的输出送入到第二个LSTM层中,会生成最终的输出数据。

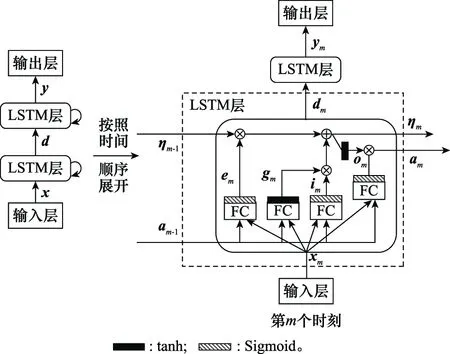
图1 LSTM神经网络的原理图Fig.1 Schematic diagram of LSTM neural network

图1右侧给出了按照时间顺序遍历LSTM层的网络结构。以第个时刻的第一个LSTM层为例,首先将数据和前一时刻的短期记忆单元-1输入到4个FC层中,会生成遗忘门向量、输入门向量、输出门向量和暂时状态向量,具体表示为

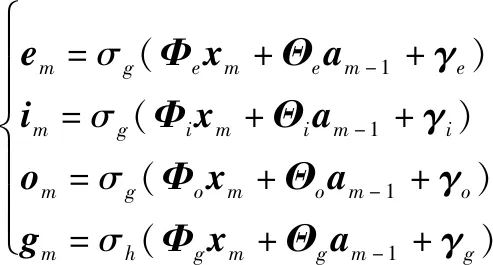
(9)

式中:,表示FC层的权重矩阵;表示偏置向量;(·),(·)分别表示Sigmoid激活函数和tanh激活函数。

然后,通过遗忘门丢弃-1的部分信息,并添加输入门选择的新信息,可生成第个时刻的长期记忆单元,再通过输出门进行滤波,可生成第个时刻的短期记忆单元,即中间向量,具体表示为

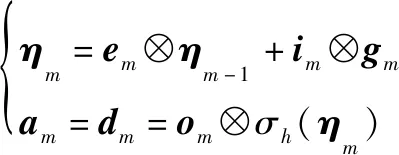
(10)

式中:⊗表示矩阵的哈达玛积。

最后,将输入到第个时刻的第二个LSTM层中,并执行式(9)和式(10)的过程,可得到第个时刻最终的输出向量。此外,长期记忆单元和短期记忆单元也将被送入第+1时刻的LSTM层中作为输入。

2.2 新型的基于LSTM网络的信道预测方法

新方法主要通过对历史时刻CSI的相关矩阵进行特征值分解来实现对基扩展模型的改进,并根据历史接收的导频信号获得历史信道的基系数估计,再利用该基系数估计构造样本,对LSTM神经网络进行线下训练和线上预测,获取未来时刻的信道预测。新方法具体描述如下:

(1) 采用BEM进行信道建模,获取历史信道的基系数估计

常用的BEM有复指数BEM、广义复指数BEM以及多项式BEM等。然而,这些现有的模型比较固定,并不能真实地反映实际变化的信道,因此存在较大的建模误差。

在高速移动场景下,由于前后车辆在同一位置处经历的信道具有很强的相关性,本文将从历史时刻CSI的相关矩阵中求解最佳的基函数,实现了对BEM的改进,并利用改进后的BEM重新拟合时域信道,这将使得信道建模更加精确,更能准确地表征当前信道状态。

若在接收端已知第个时刻的理想频域信道信息,则可根据信道信息获取信道的相关矩阵,即

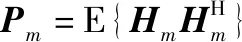
(11)

式中:=[(0),(1),…,(),…,(-1)],其中()是第个符号第个子载波的理想频域信道系数。

对相关矩阵进行特征值分解,可以得到

=

(12)

式中:是的特征值组成的对角阵;代表特征向量矩阵,的第1列到第列组成最佳基函数,即

=(∶,1∶)

(13)

基于最优基函数矩阵,对信道进行建模,然后利用历史时刻接收的导频信号和最小二乘(least squares, LS)估计方法可以估计得到第个符号的基系数估计值:

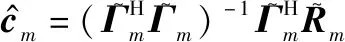
(14)

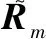
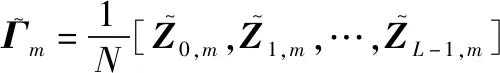
(15)

其中,

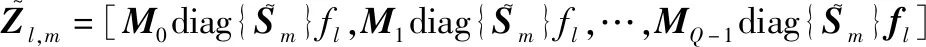
(16)

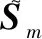
(2) 利用LSTM神经网络进行信道预测

由于复值神经网络架构繁杂,所需神经元数目较多,导致在线下训练网络和线上进行预测时会引起较长的运行时间,并产生较大的复杂度。本文将样本数据的实部和虚部进行分离,采用两个实值网络分别预测基系数的实部与虚部,且两个实值网络的参数设置保持一致。

① 数据预处理及线下训练

对式(14)获得的历史基系数估计以及目标基系数进行正则化处理,处理后的样本数据按照1∶1的比例划分为实部、虚部训练集,和实部、虚部测试集,,训练集表示为

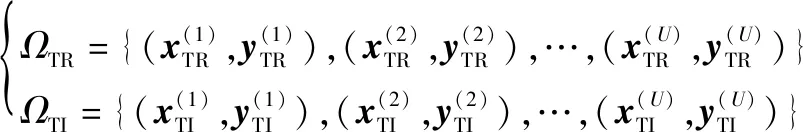
(17)

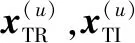
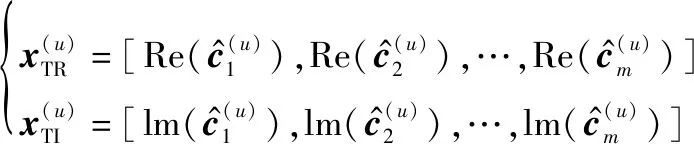
(18)

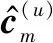
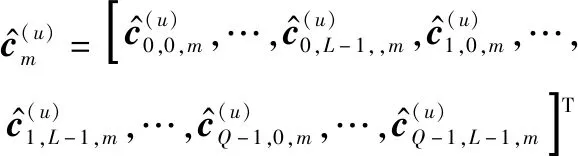
(19)

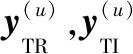
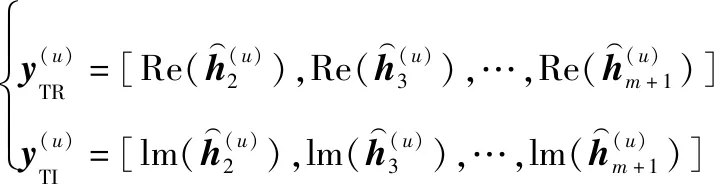
(20)

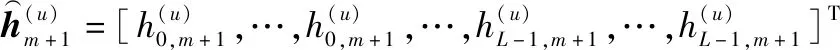
(21)

本文将损失函数表示为网络输出的时域信道系数预测值与目标时域信道系数的均方误差(mean square error,MSE)。通常,损失函数可以表示为

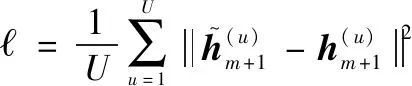
(22)

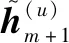
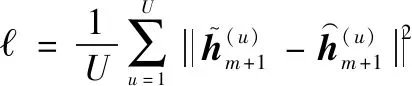
(23)

在网络训练过程中,为了避免梯度下降、出现局部最优情况,本文使用小批量梯度下降算法,并利用Adam方法对梯度进行反向更新。为避免网络模型出现过拟合现象,神经元在训练过程中使用Dropout方法,即输入层和隐藏层的神经元以一定概率不参与神经网络的训练。一旦训练完成,该网络模型就可以用于预测未来时刻的时域信道信息。

② 线上预测阶段

线上预测就是将测试集中的任意样本送入到两个训练好的实值神经网络中,然后由网络输出预测结果。实部、虚部测试集,表示为

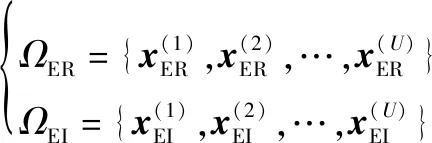
(24)

其中,

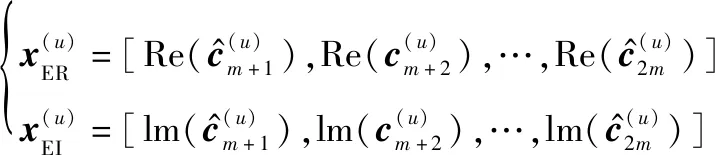
(25)

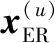
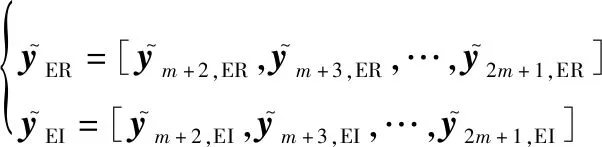
(26)

最终得到的时域信道系数预测值为

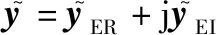
(27)

式中:j是虚数单位。

3 计算机仿真与分析

3.1 计算机仿真

本节将对新方法进行仿真与分析,以验证其预测性能。本文考虑的是一个单入单出的OFDM系统,仿真过程中,采用的是两层LSTM网络。表1给出了具体的仿真参数。

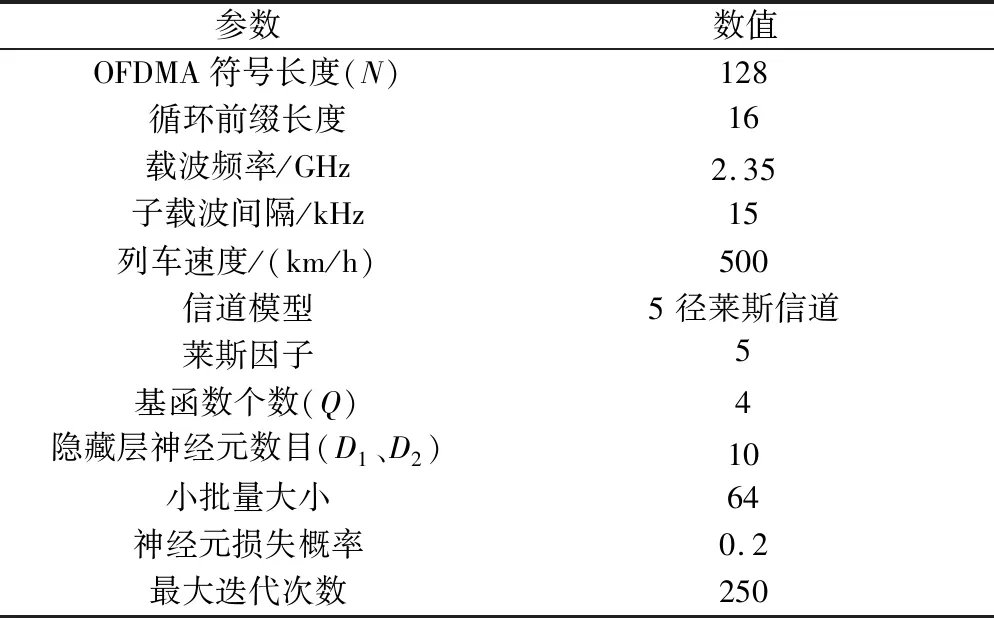
表1 仿真参数Table 1 Simulation parameters

为了验证本文所提方法的性能,仿真还对比了文献[7]基于BP神经网络和文献[9]基于两层LSTM神经网络的预测性能。其中,文献[7]是利用历史时刻的时域信道系数预测未来时刻的时域信道系数,在网络训练过程中,其逼近目标为理想的时域信道系数。文献[9]是基于LSTM神经网络,对连续的时域信道响应进行预测,在网络训练过程中,其逼近目标为理想的时域信道信息。

图2给出了新方法采用不同训练样本数目时的MSE性能。仿真中,导频数目设置为32。从图中可以看出,随着训练样本数目的增加,新方法的预测性能有所提高,但是当训练样本数大于1 000时,新方法的性能不再提高,这是由于训练数目太多,导致网络模型出现过拟合现象,且训练样本数目的增加将延长训练时间,如表2所示,因此新方法在后面的仿真中将选择训练样本数为1 000。

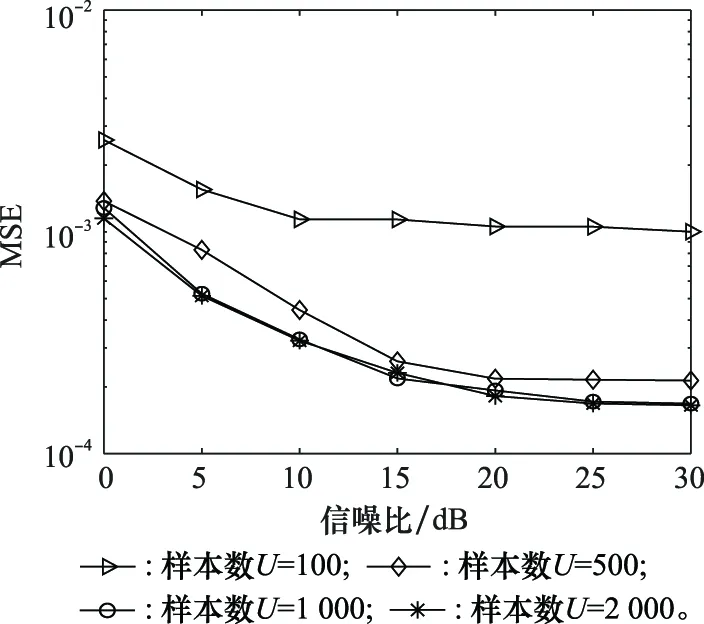
图2 新方法在不同训练样本数目时的MSE性能(Np=32)Fig.2 MSE performance of the proposed method with different number of training samples (Np=32)

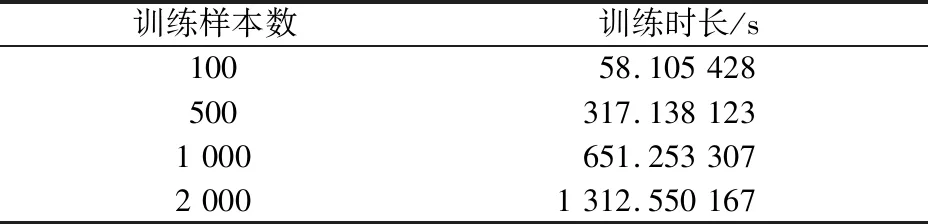
表2 样本数目不同时的训练时长Table 2 Training time at different number of samples

图3给出了所提方法在不同导频数目下的预测性能。从图中可以看出,随着导频数目的增加,新方法的预测性能也逐渐提升,这是因为导频数目越多,所包含的历史信息越多,使得估计的基系数就越准确。但是,大量导频会增加估计基系数的复杂度,而且会降低通信系统的传输效率,因此在实际通信系统中应该合理选择导频数目。

图3 所提方法采用不同导频数目时的MSE性能Fig.3 MSE performance of the proposed method with different number of pilot freguency

图4给出了各种信道预测方法在不同逼近目标时的MSE性能,即分别逼近理想信道系数和基于LMMSE方法估计的信道系数。从图中可以看出,不论哪种预测方法,逼近理想信道的性能均优于LMMSE估计信道的性能,这是由于利用理想信道训练得到的网络模型精度更高。然而,在实际通信中,理想的信道信息往往是未知的,其需要通过估计/预测/反馈的方式获取,因此新方法主要采用基于LMMSE方法获得的信道估计作为目标。与文献[7]相比,不论逼近哪种信道信息,新方法均可以取得更优的预测性能,这是因为文献[7]所采用的BP神经网络模型结构简单,没有充分考虑到信道系数在不同时刻的时间相关性,因此其预测精度不高。相比文献[9],在低信噪比时,新方法的性能更优,这是由于文献[9]利用LS与线性内插方法来获取历史CSI比新方法仅利用LS方法获取历史基系数在低信噪比情况下的估计精度更差,利用误差较大的历史CSI构造输入样本将导致与实际CSI误差较大,因此文献[9]的方法预测精度不高。然而,在高信噪比情况下,新方法的性能有所下降,这是由于随着信噪比的增大,文献[9]利用LS与线性内插方法获取的历史CSI精度提高了,且该方法利用了所有的历史CSI来进行信道预测,这将使得获取的信道特征更加丰富,而新方法采用基扩展模型在信道建模时引入建模误差,因此导致性能上有所损失。但是,新方法采用历史时刻的基系数来预测时域信道系数,相比现有方法减少了预测参数的数目,降低了计算复杂度。

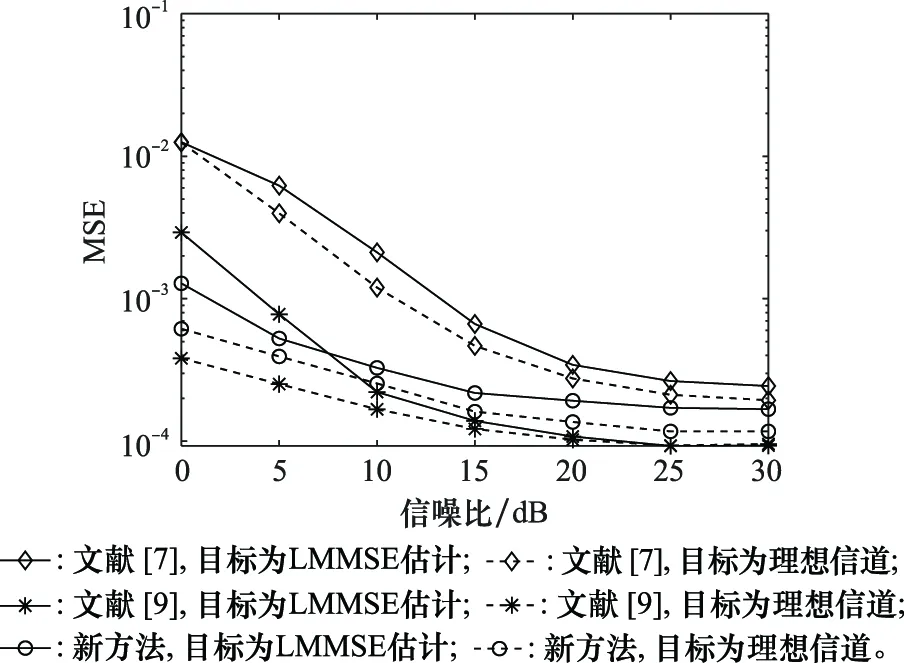
图4 不同信道预测方法的MSE性能(U=1 000,Np=32)Fig.4 MSE performance of different channel prediction methods (U=1 000, Np=32)

3.2 复杂度分析

本节将对不同方法的复杂度进行分析,在此主要比较了文献[7]、文献[9]以及新方法的计算复杂度,每种方法的计算复杂度均包括获取历史信息、线下训练与线上预测3个部分。

表3给出了各种预测方法计算复杂度的比较分析,其中计算复杂度用浮点计算量(FLOPs)表示。为了更清楚地看出各种方法的计算复杂度,在此给出了当=128,=5,=4,=1 000,==10,=32时各种方法的计算复杂度,如表3最后一列所示。从表3可以看出,文献[7]方法的计算复杂度最低,但是其预测性能收益最小。新方法在获取历史信息时虽然增加了计算基函数矩阵和估计基系数的复杂度,但新方法的性能更优;与文献[9]相比,新方法使用基系数预测替代全部CSI预测,减少了预测参数的数目,降低了网络在线下训练和线上测试阶段的复杂度。

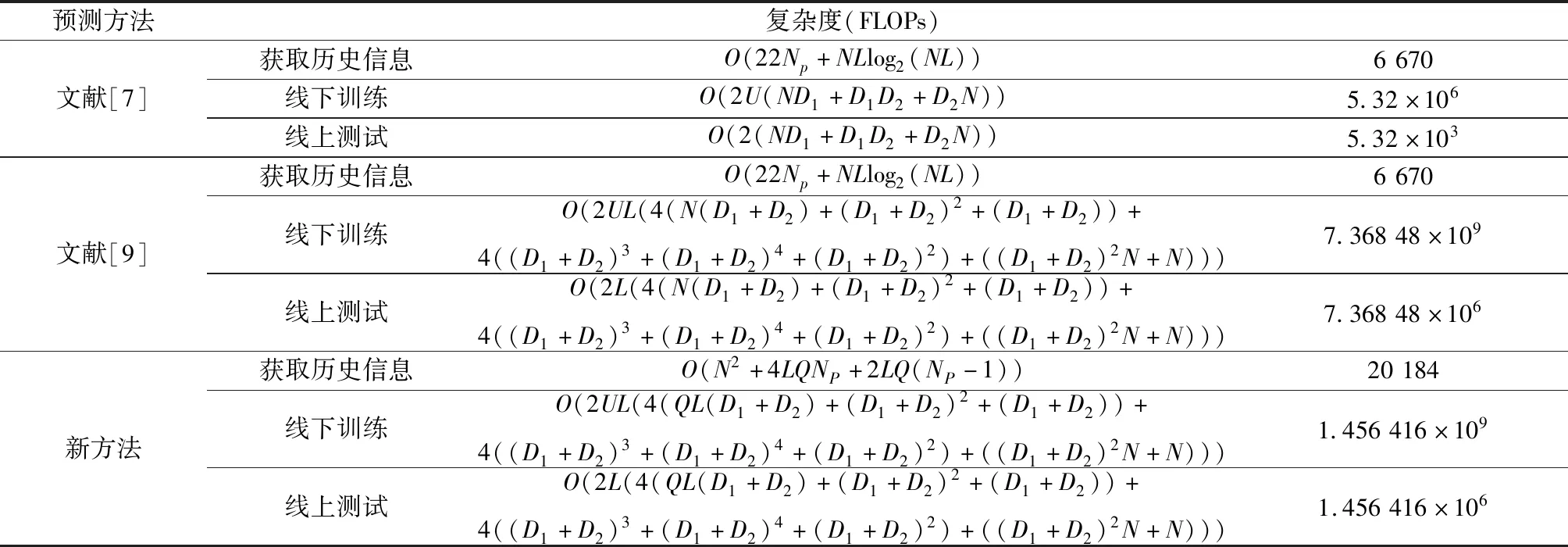
表3 各种方法的计算复杂度分析Table 3 Complexity analysis of various methods

4 结 论

针对高速移动场景下的单入单出OFDM系统,本文提出了一种BEM下基于LSTM神经网络的时变信道预测方法。新方法利用历史时刻CSI的相关矩阵对BEM进行改进,且采用基系数预测未来时刻的信道系数,减少了预测参数的数量,降低了计算复杂度。此外,为了使信道预测模型更加符合实际通信系统,新方法在线下网络训练的过程中,将基于LMMSE方法估计的时域信道系数作为目标,大大增强了信道预测模型的实用性,是一种具有高精度和可靠性的时变信道预测方法。