基于罗德里格斯参数的惯性系传递对准算法

徐 庚, 何永旭, 张勇刚

(哈尔滨工程大学智能科学与工程学院, 黑龙江 哈尔滨 150001)

0 引 言

初始对准即确定惯导系统的初始姿态,而传递对准则是一种特殊的惯导系统动基座初始对准技术,低精度子惯导系统(子惯导)依靠高精度主惯导系统(主惯导)提供的导航信息,可以在较短时间内实现初始对准以及器件主要误差的标定。因此,传递对准技术被广泛应用于军事武器装备中。

由于主惯导系统的精度要远高于子惯导,且主惯导的姿态矩阵是已知的,所以传递对准的首要目的是确定主、子惯导之间的姿态矩阵,然而主、子惯导通常安装在不同的位置,两者之间存在未知的安装误差角以及杆臂误差,这导致子惯导会敏感不同的物理信息。通常主、子惯导之间的杆臂可以通过预先测量进行补偿。然而,对于一些大型载体,如舰船,由于子惯导位于甲板上,主惯导安装在内部舱室中,精确测量两者之间的杆臂是较为困难的,尽管可以通过测量补偿大部分的杆臂误差,但是残余杆臂误差仍会对传递对准精度产生影响。除此之外,子惯导传感器(陀螺仪和加速度计)误差也是影响武器装备发射后纯惯性导航精度的主要因素。因此,传递对准需要同时对安装误差角、残余杆臂误差和传感器误差进行估计。

现有的传递对准算法主要分为两类:基于优化方法的传递对准算法和基于滤波方法的传递对准算法。文献[11]将文献[1]提出的优化对准思想引入传递对准中,提出了基于q-method的“传递粗对准”方法,将传递对准问题转化为姿态估计领域中经典的Wahba问题。然而,该方法只能粗略估计出主、子惯导之间的安装误差角。文献[12]利用主、子惯导的角速度和比力关系建立代价函数,采用奇异值分解方法(singular value decomposition, SVD)求解主、子惯导之间的姿态矩阵,在此基础上,进一步计算出子惯导的传感器零偏。尽管基于优化方法的传递对准算法无需先验参数,但是其要求待估计参数为常值,且主、子惯导之间的杆臂误差已完全补偿。然而,当主、子惯导之间的姿态矩阵和子惯导传感器零偏为时变值,或存在残余杆臂误差时,基于优化方法的传递对准算法的对准性能会受到极大的影响,所以其应用范围存在一定限制。

基于滤波方法的传递对准算法是传递对准领域的主流研究方向,该类型算法在误差模型的基础上,利用主、子惯导输出的导航信息的差值估计安装误差角、传感器误差等参数。常用的误差模型包括角误差模型和角误差模型,然而,当失准角为大角度时(子惯导导航参数的初始化通常为主惯导导航参数一步装订,所以大失准角问题主要由大安装误差角导致),两种模型的状态误差方程都为非线性,且非线性度较强,尽管可以采用非线性滤波进行状态估计,但是算法复杂度较大,且对准精度相对较低。

为了解决大失准角问题,另一种较好的思路是在惯性系下进行传递对准。惯性系对准思想最早由文献[1]和文献[21]提出,文献[22]基于惯性系对准思想建立了惯性系下的非线性初始对准模型。文献[23]则将惯性系对准思想引入传递对准中,建立了惯性系下的非线性传递对准模型。文献[13]则在文献[23]的基础上提出了一种惯性系下任意安装误差角传递对准模型。通过构建角速度积分和比力积分的匹配方案,利用矩阵卡尔曼滤波(matrix Kalman filter, MKF)直接对常值姿态矩阵进行状态估计,无需对安装误差角的大小有任何假设。该算法在建模时要求对主、子惯导之间的杆臂误差进行补偿,然而当残余杆臂误差较大时,残余杆臂误差会对传递对准的精度产生影响,因此有必要对残余杆臂误差进行估计。

针对大失准角问题以及残余杆臂误差问题,本文在文献[13]的基础上,将残余杆臂误差列为待估计状态量,采用罗德里格斯参数等价替代该常值姿态矩阵,并考虑了低精度子惯导器件的零偏不稳定性影响,推导了关于罗德里格斯参数和残余杆臂误差具有弱非线性量测方程(状态误差方程仍为线性)的传递对准模型。相比现有的传递对准算法,本文提出的惯性系传递对准算法在系统维数上与传统模型相同,但非线性度大大降低,有效地解决了大失准角问题以及残余杆臂误差问题。

1 主、子惯导测量值关系

首先,对本文涉及的符号及其含义做统一说明,如表1所示。

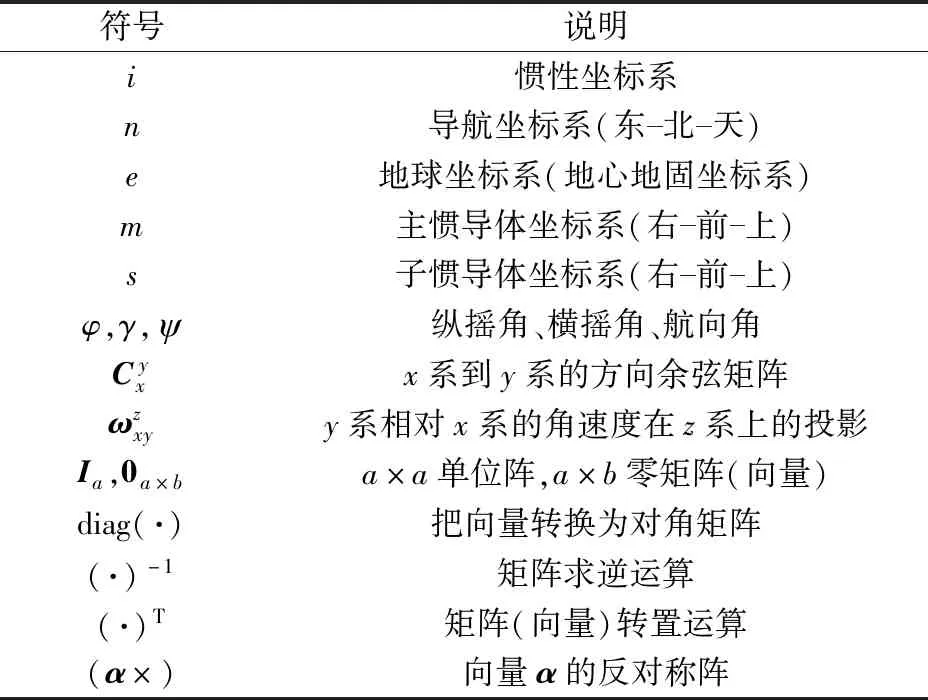
表1 符号说明Table 1 Nomenclatures

由于主、子惯导空间位置不同,两者会敏感不同的物理量,其传感器(陀螺仪和加速度计)的理想测量值之间的关系可以表示为

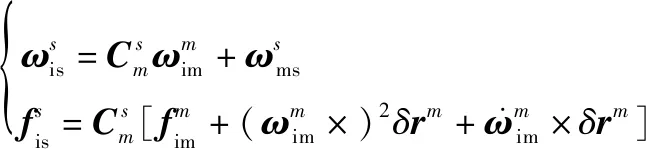
(1)

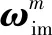
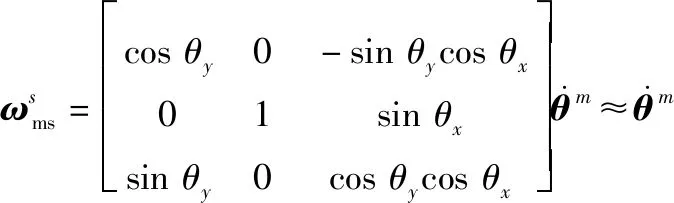
(2)

对于载体变形,不同载体的变形情况是不同的。对于机翼,由于其形状细长,且材料弹性较大,可视为悬臂梁,载弹量变化、快速机动等因素会导致机翼发生明显的变形;对于舰船,其船体尺寸大,刚性也较大,因此舰船的变形与机翼相比有所不同。文献[24]指出舰船的静态变形主要由载荷变化、日晒不均等因素导致;动态变形主要由海浪冲击、船体运动及转舵操作等因素导致。文献[25]采用像机链位姿传递摄像测量法测量船舶的动态变形,发现船舶在大机动下(如转弯),船体会出现明显的变形。然而,由于舰船吨位较大,实际航行过程一般十分平稳,且难以在短时间内实现大机动,所以实际载体变形相对较小,或在短时间内可视为常值。因此,针对舰载惯导系统的传递对准问题,本文忽略载体变形的影响,更多关于载体变形处理方法的对比和分析可参考文献[26]。值得说明的是,当存在载体变形时,杆臂和变形会产生耦合,进而导致动态杆臂,相对于仅考虑常值杆臂,在传递对准模型中建模动态杆臂有利于改善对准结果。

2 子惯导传感器误差建模

子惯导传感器的误差建模决定了传递对准状态误差方程的形式,并对传递对准精度有较大影响,是传递对准研究的一个重要环节。传感器误差包括常值误差和随机误差,理论上,对所有误差源进行建模并估计,可以得到最好的估计结果,但在实际应用中,仅需针对性地估计其中占据主导地位的误差源。

对于低精度子惯导而言,如微机电系统(micro-electro-mechanical system, MEMS),常值误差中的启动零偏在每次子惯导开机上电时,会发生很大的变化,是传递对准中必须估计的误差项。随机误差中的主要误差项包括角度(速度)随机游走和零偏不稳定性。角度(速度)随机游走是白噪声的积分,白噪声在误差模型中为快变部分;零偏不稳定性表征传感器的时变零偏,通常建模为一阶马尔可夫过程,在误差模型中表现为缓变部分,而且传感器精度越低,零偏不稳定性的影响越大。综合上述分析,对于低精度子惯导传感器,建模时需要考虑的是启动零偏、角度(速度)随机游走和零偏不稳定性,即:

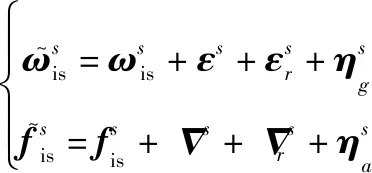
(3)

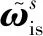
对于启动零偏,其微分方程为

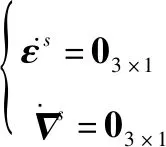
(4)

对于零偏不稳定性,将其建模为一阶马尔可夫过程,微分方程为

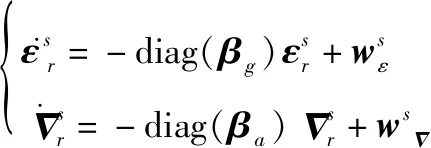
(5)

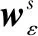
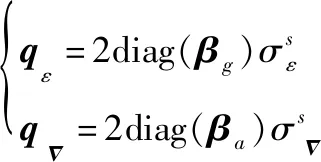
(6)

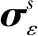
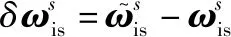
(7)

3 改进的惯性系传递对准算法

对子惯导姿态矩阵进行链式分解,可得

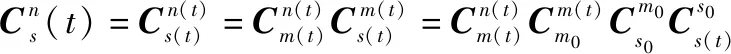
(8)

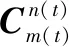
(9)

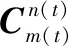
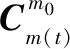
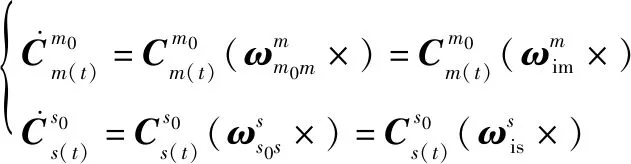
(10)

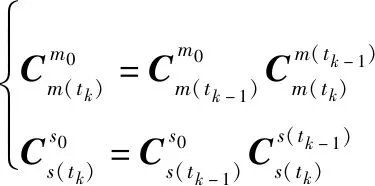
(11)

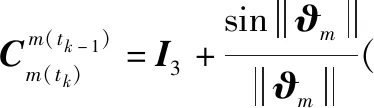
(12)

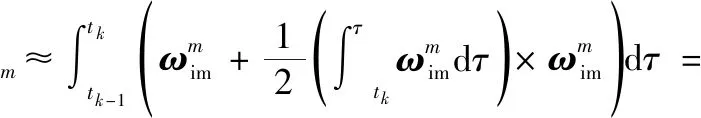
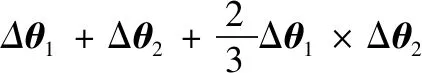
(13)

式中:Δ和Δ表示主惯导陀螺仪在时间段[-1,]内的两次角增量采样。

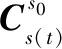
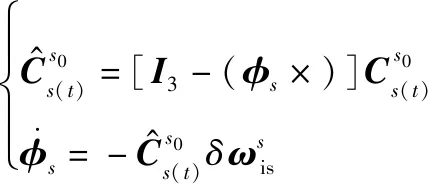
(14)

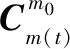
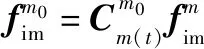
(15)

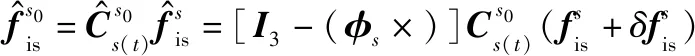
(16)

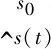
(17)

结合式(1)和式(17),可得

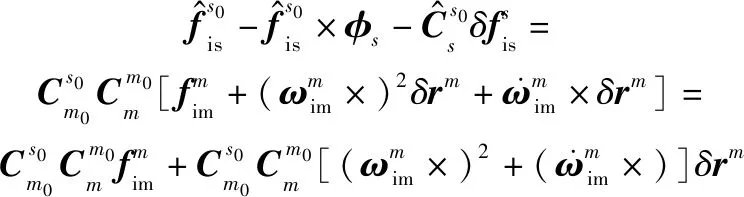
(18)

在传递对准过程中,残余杆臂误差δ假设为固定值,所以有:

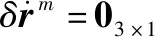
(19)

同理,对子惯导陀螺仪的测量值进行相同处理(忽略载体变形),可得

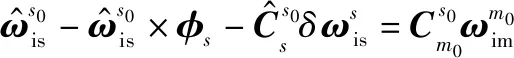
(20)

对式(18)和式(20)两边进行积分,记:

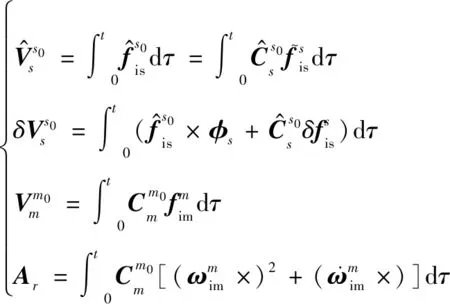
(21)

(22)

由式(18)、式(20)～式(22),可得

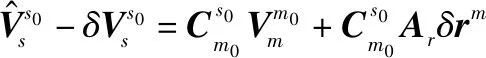
(23)

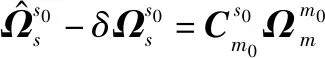
(24)

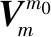
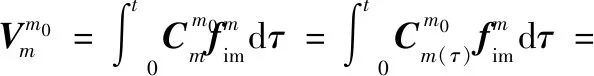
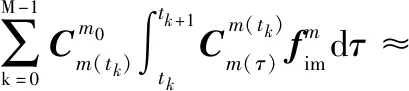
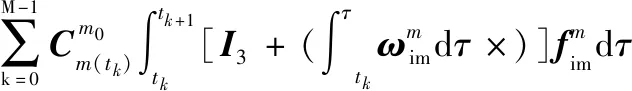
(25)

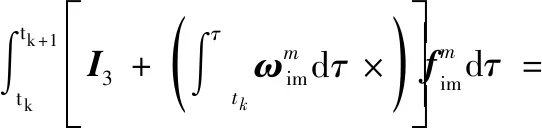
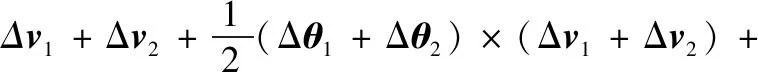
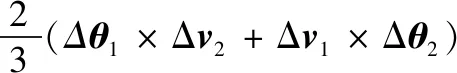
(26)

(27)

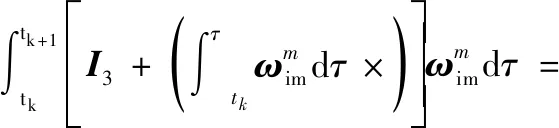
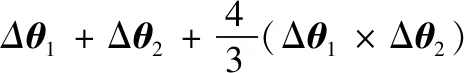
(28)

式中:==,Δ和Δ表示主惯导加速度计在时间段[-1,]内的两次速度增量采样。

利用方向余弦矩阵的微分性质,可得

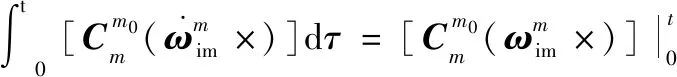
(29)

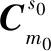
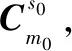
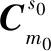
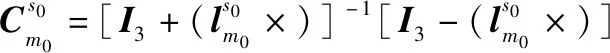
(30)

显然有:

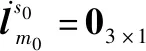
(31)

将式(30)代入式(23)和式(24)中,可得

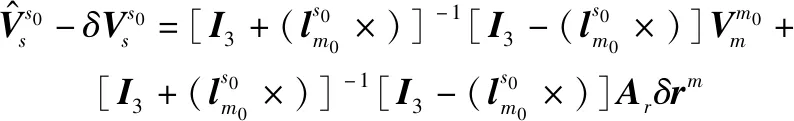
(32)

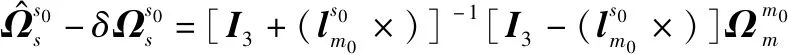
(33)

化简式(32)和式(33)可得

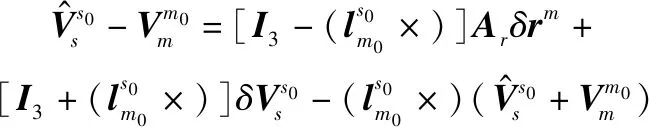
(34)

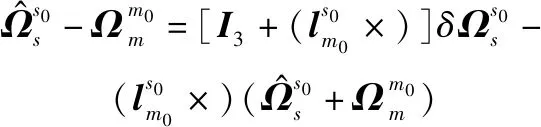
(35)

结合式(4)、式(5)、式(14)、式(19)、式(31)、式(34)和式(35),可以得到如下的状态误差方程和量测方程:

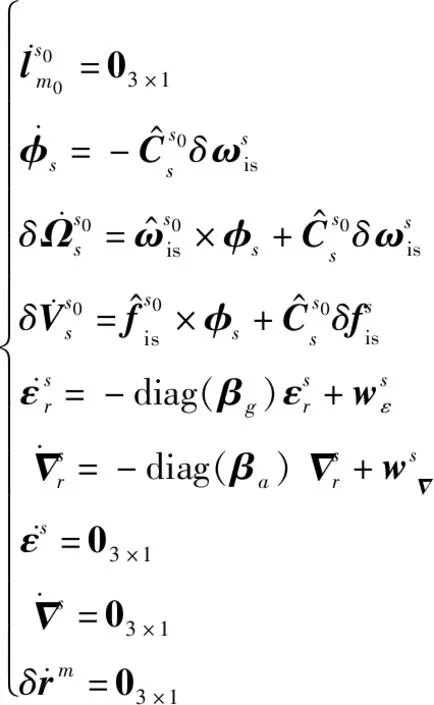
(36)

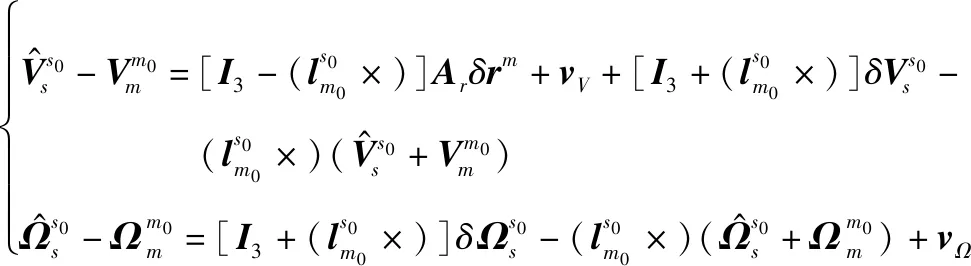
(37)

式中:和为量测噪声。

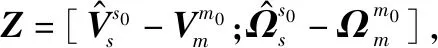
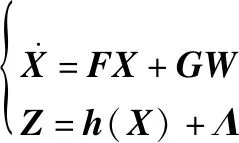
(38)

式中:状态转移矩阵、状态噪声分配矩阵和非线性量测函数(·)可由式(36)和式(37)得到。

上述传递对准模型的系统维数为27,相比于传统的传递对准模型,如角误差模型(也同时估计残余杆臂误差和传感器零偏不稳定性),系统维数保持不变,但模型的非线性度大大降低。

由于传递对准模型的量测方程为非线性,需要采用非线性滤波器进行状态估计,常用的非线性滤波器有扩展卡尔曼滤波器(extended Kalman filter, UKF)、无迹卡尔曼滤波器(unscented Kalman filter, UKF)和容积卡尔曼滤波器(cubature Kalman filter, CKF)等,鉴于该模型的非线性度较弱,本文拟采用EKF和UKF两种典型的非线性滤波器。

综合上述分析,可得到如图1所示的惯性系传递对准算法流程图。

图1 惯性系传递对准算法流程图Fig.1 Flow chart of inertial-frame-based transfer alignment method

4 仿真与分析

为了验证本文提出算法的有效性,本节设计了基于船舶摇摆运动的仿真实验。

4.1 仿真参数设置

受风浪影响,船舶在海上航行时,其运动可采用一组正弦函数进行描述:

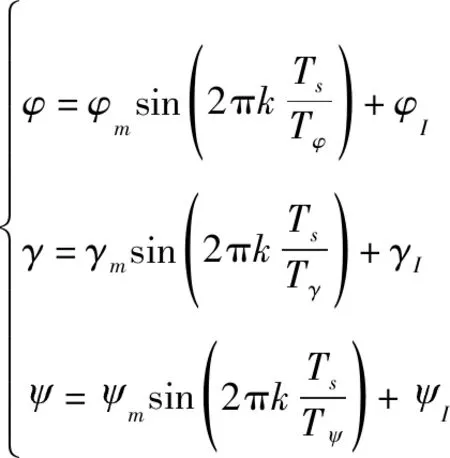
(39)

式(39)中相关参数设置如表2所示。子惯导传感器参数设置如表3所示。

表2 摇摆运动参数Table 2 Parameters for sway motion

表3 子惯导传感器参数Table 3 Sensor specifications of slave INS

仿真其他参数设置:主、子惯导之间的安装误差角=[15°;15°;30°],残余杆臂误差δ=[2 m;2 m;1 m],传递对准时间=30 s。此外,为了验证本文提出方法的有效性,本文选取基于UKF的角误差模型传递对准算法(简称为“UKF-TA”)、文献[12]提出的基于SVD的传递对准算法(简称为“SVD-TA”)、文献[13]提出的基于MKF的任意安装误差角传递对准算法(简称为“MKF-TA”,并增加了对传感器零偏不稳定性的估计),作为对比方法。本文提出的算法分别采用EKF和UKF进行状态估计(简称为“EKF-ITA”和“UKF-ITA”)。

4.2 仿真结果及分析

仿真结果如图2～图8所示。图2为姿态误差角在传递对准过程中的变化曲线,可以看出,随着对准时间的增加,姿态误差角基本呈线性增长,其主要由子惯导陀螺仪误差导致。尽管姿态误差角随时间不断增大,但其在较短的传递对准时间内仍然可以保持为小角度,到对准结束时刻误差角仍未超过2°,所以式(14)中线性微分方程的假设成立。然而,如果对准时间更长或子惯导陀螺仪误差更大,姿态误差角可能会逐渐变为大角度,此时可以采用反馈校正对姿态误差角进行补偿,从而保证姿态误差角始终为小角度。

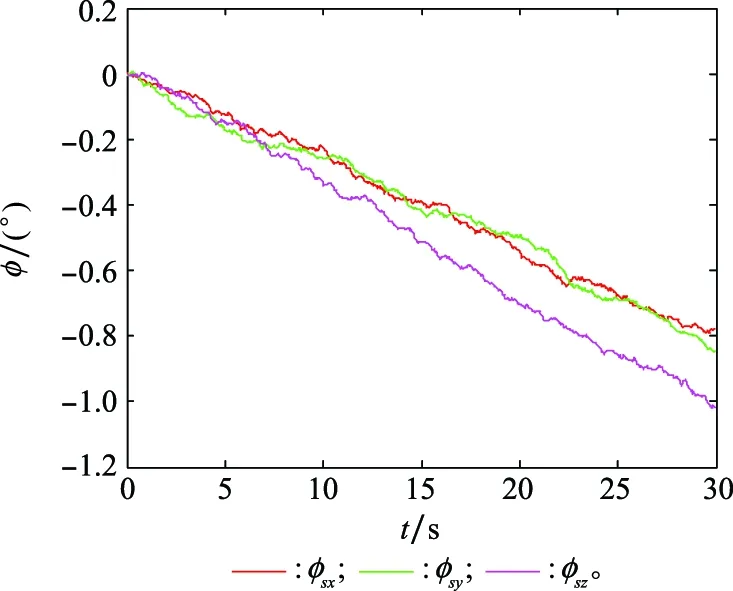
图2 姿态误差角φs变化曲线Fig.2 Curves of attitude errors φs

图3～图5为安装误差角的估计结果,表4为安装误差角在20～30 s的估计误差的均值和均方根(root mean square, RMS)。

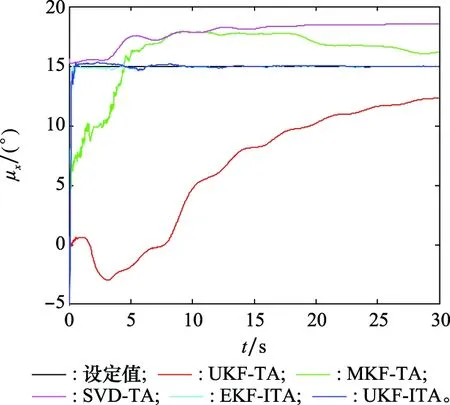
图3 安装误差角估计结果Fig.3 Estimates of installation error angle

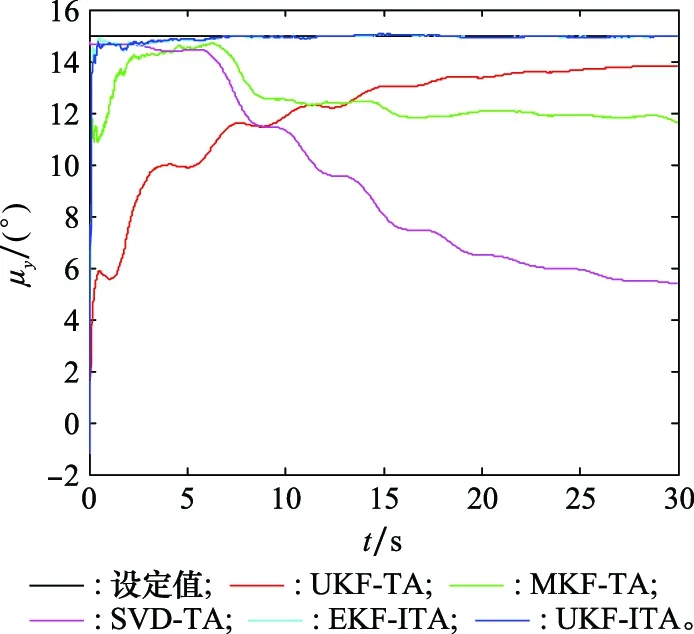
图4 安装误差角估计结果Fig.4 Estimates of installation error angle

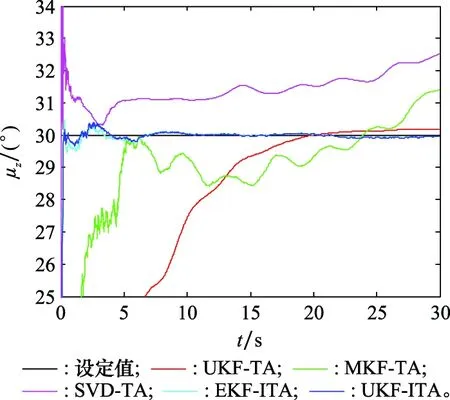
图5 安装误差角估计结果Fig.5 Estimates of installation error angle

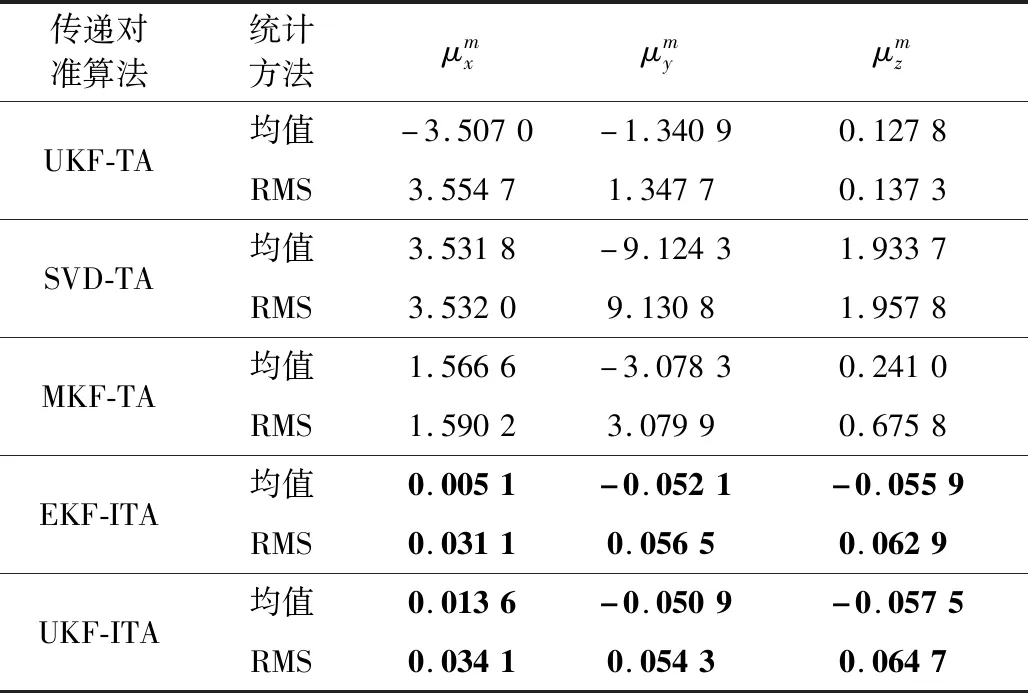
表4 安装误差角估计误差的均值和RMS (20～30 s)Table 4 Means and RMS of the estimate errors of the installation error angle (20～30 s) (°)

由于主惯导的姿态是已知的,且主、子惯导之间的姿态矩阵为常值矩阵,所以可以采用安装误差角的估计精度作为传递对准精度的评判标准。由图3～图5可以看出,相比于UKF-TA、MKF-TA和SVD-TA,本文提出的EKF-ITA和UKF-ITA具有更高的估计精度和更快的收敛速度,在5～10 s内即可完成传递对准。由于安装误差角为大角度,导致角误差模型为非线性,且模型的非线性度较强,UKF-TA的估计结果存在明显的估计误差,且收敛速度较慢。由于SVD-TA要求子惯导传感器误差为常值,且杆臂误差已补偿,当子惯导传感器精度较低且杆臂误差未完全补偿时,时变的零偏不稳定性和残余杆臂误差导致SVD-TA的估计结果是发散的。事实上,相比于时变的传感器误差,残余杆臂误差对SVD-TA估计效果的影响更大。文献[12]针对SVD-TA的使用条件也做了明确说明:“子惯导应补偿由杆臂误差导致的加速度”,因此在本文的仿真中,SVD方法的效果不佳。由于MKF-TA未对残余杆臂误差进行估计,所以残余杆臂误差也对MKF-TA的估计精度产生明显影响,导致其估计结果无法收敛。对于EKF-ITA和UKF-ITA,两者的估计结果在收敛速度和收敛精度方面十分相似,并无显著差别,由于EKF-ITA的计算量要小于UKF-ITA,采用最基本的EKF即可满足需求。对比平稳阶段安装误差角估计误差的均值和RMS也可以看出,相比其他方法,本文提出的EKF-ITA和UKF-ITA具有更小的估计误差。

图6为残余杆臂误差的估计结果,由于SVD-TA和MKF-TA未对残余杆臂误差进行估计,图6仅列出UKF-TA、EKF-ITA和UKF-ITA的估计结果。可以看出,在大失准角下,UKF-TA存在较大的估计误差,而EKF-ITA和UKF-ITA在较短时间内即可完成收敛,且估计精度相对较高,估计误差在厘米级范围。

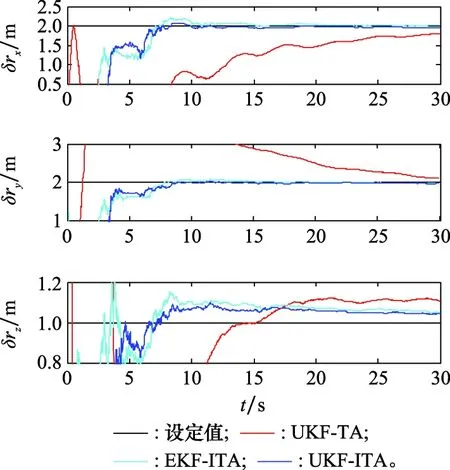
图6 残余杆臂误差δrm估计结果Fig.6 Estimates of residual lever arm error δrm

图7和图8为陀螺仪和加速度计零偏的估计结果,而零偏为启动零偏和零偏不稳定性之和。可以看出,本文提出的EKF-ITA和UKF-ITA对于传感器零偏的估计结果相对更为稳定且精度更高,而UKF-TA、MKF-TA和SVD-TA的估计结果是发散的,无法准确估计出传感器的零偏。

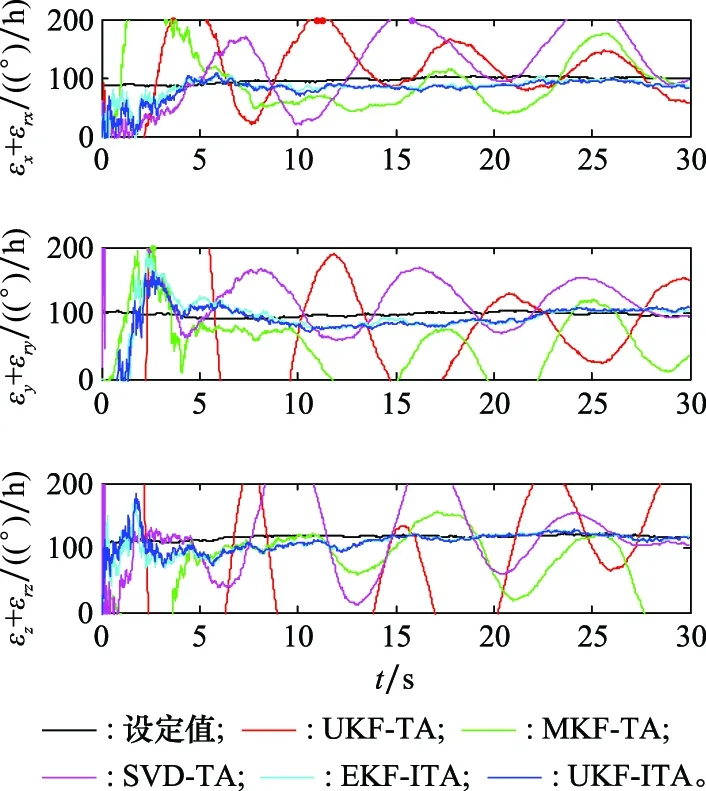
图7 陀螺仪零偏(启动零偏和零偏不稳定性)估计结果Fig.7 Estimates of gyro bias (turn-on bias and bias instability)

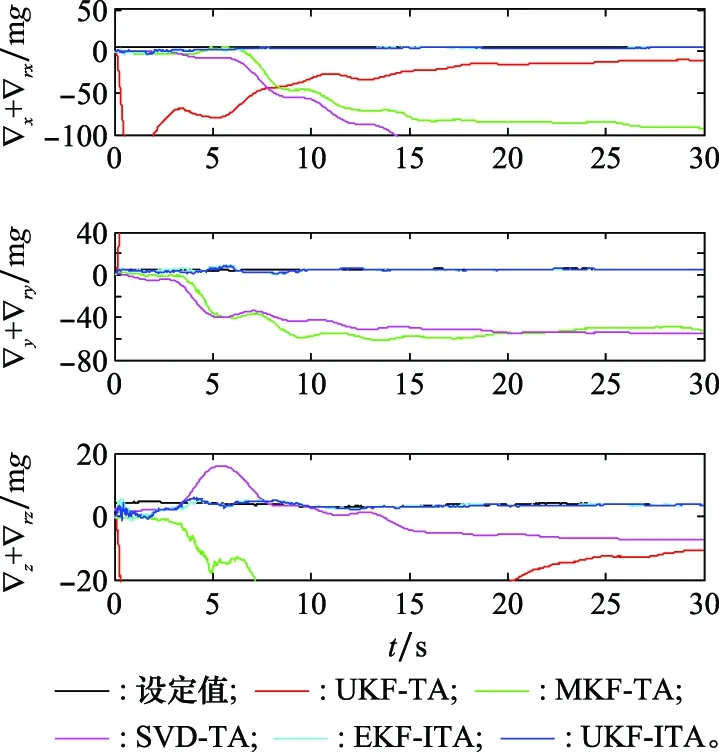
图8 加速度计零偏(启动零偏和零偏不稳定性)估计结果Fig.8 Estimates of accelerometer bias (turn-on bias and bias instability)

由上述仿真结果可以看出,本文提出的算法通过估计残余杆臂误差和传感器零偏不稳定性,极大地提高了对准和传感器标定的精度,有效地解决了残余杆臂误差和传感器零偏不稳定性对传递对准的影响。

5 试验与分析

本节利用车载试验数据进一步验证本文提出算法的有效性。

5.1 试验环境及条件

车载平台和设备示意图如图9所示。其中,试验设备包括自研低精度惯性测量单元(inertial measurement unit, IMU)、IXSEA公司高精度惯导系统(photonic inertial navigation system, PHINS)和全球定位系统(global positioning system, GPS)接收机。IMU输出频率为200 Hz,内置三轴陀螺仪和加速度计,可以测量载体轴向的角速度和比力,其相关参数如表5所示。

图9 车载平台与设备安装示意图Fig.9 Diagram of field test vehicle and equipment

表5 IMU传感器参数Table 5 Sensor specifications of IMU

鉴于该IMU的零偏不稳定性误差较小,所以本试验忽略其零偏不稳定性的影响。PHINS在GPS辅助下可构成组合导航系统,并为IMU提供高精度导航信息(姿态、速度和位置),输出频率为50 Hz,但是未提供惯性测量信息。PHINS和IMU共同安装在一个金属板上,可忽略变形误差,且两者安装时轴向几乎平行,之间的安装误差角很小,但存在一定的杆臂误差。

由于PHINS没有提供惯性测量信息,惯性系传递对准算法和SVD算法无法直接进行应用;由于未对安装误差角、杆臂误差以及传感器零偏进行预先测量和标定,无法直接进行精度评判。为了解决上述两个问题,本文首先利用文献[34]提出的惯导反演算法,模拟出PHINS的惯性测量信息,再利用模拟的信息进行惯性系传递对准;然后,利用纯惯导定位精度对各方法的传递对准精度进行间接评判。上述试验流程可概括为如图10所示的结构框图。

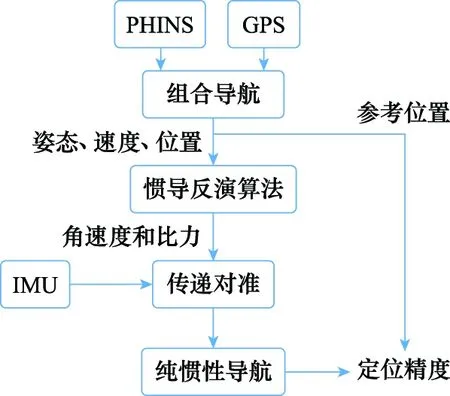
图10 试验流程图Fig.10 Flow chart of field test

车辆的轨迹和姿态变化如图11所示,其中对准阶段(30 s)包含一次转弯机动,而选择该数据段有两方面原因:一方面,转弯机动引入的姿态变化有利于激励各误差源;另一方面,转弯机动会产生杆臂加速度,会对未考虑杆臂误差的传递对准算法产生影响。传递对准结束后,利用估计的安装误差角对PHINS姿态进行修正,并作为IMU的初始姿态,而初始速度和初始位置则直接装订PHINS信息。

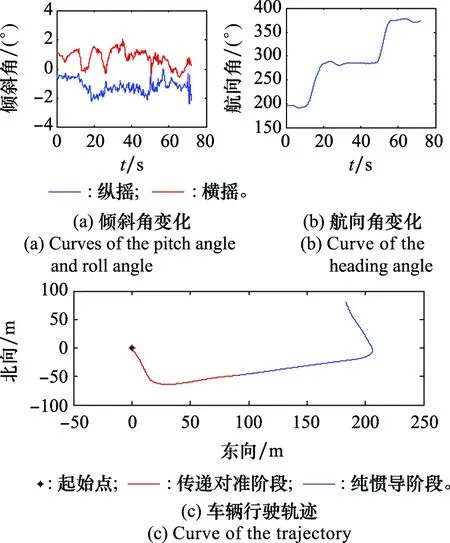
图11 车辆行驶轨迹和姿态变化Fig.11 Curves of the trajectory and attitude

5.2 试验结果及分析

试验中安装误差角的估计结果如图12～图14所示,杆臂误差的估计结果如图15所示,传感器启动零偏估计结果如图16和图17所示。图18为传递对准后纯惯导导航的定位误差。

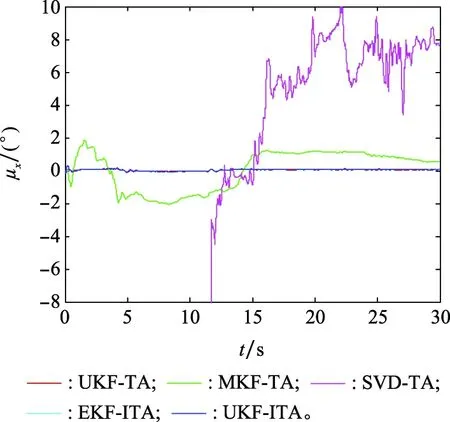
图12 安装误差角估计结果(试验)Fig.12 Estimates of installation error angle (field test)

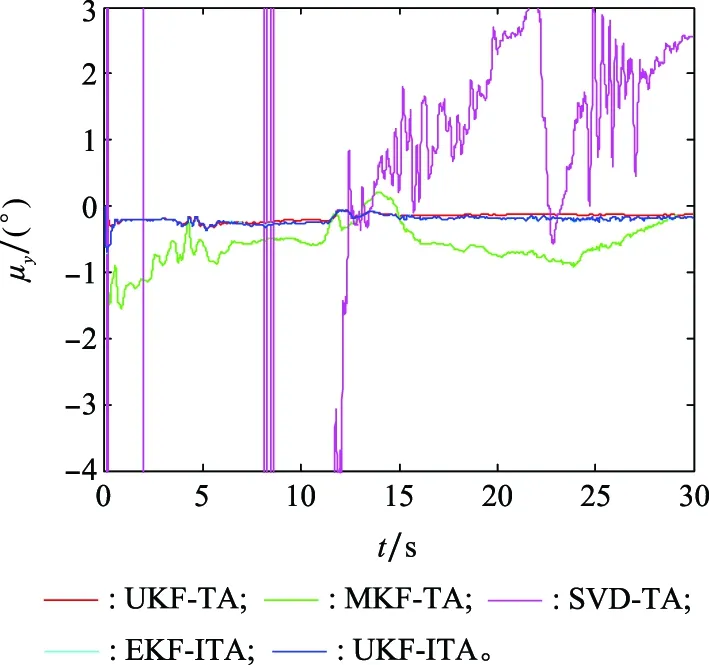
图13 安装误差角估计结果(试验)Fig.13 Estimates of installation error angle (field test)

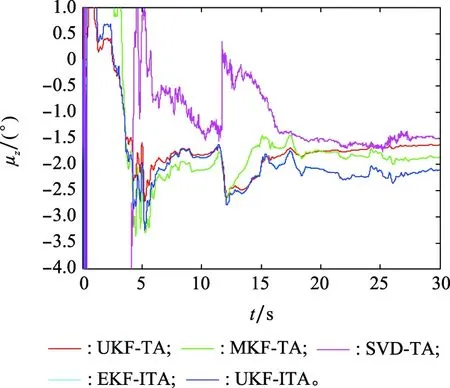
图14 安装误差角估计结果(试验)Fig.14 Estimates of installation error angle (field test)

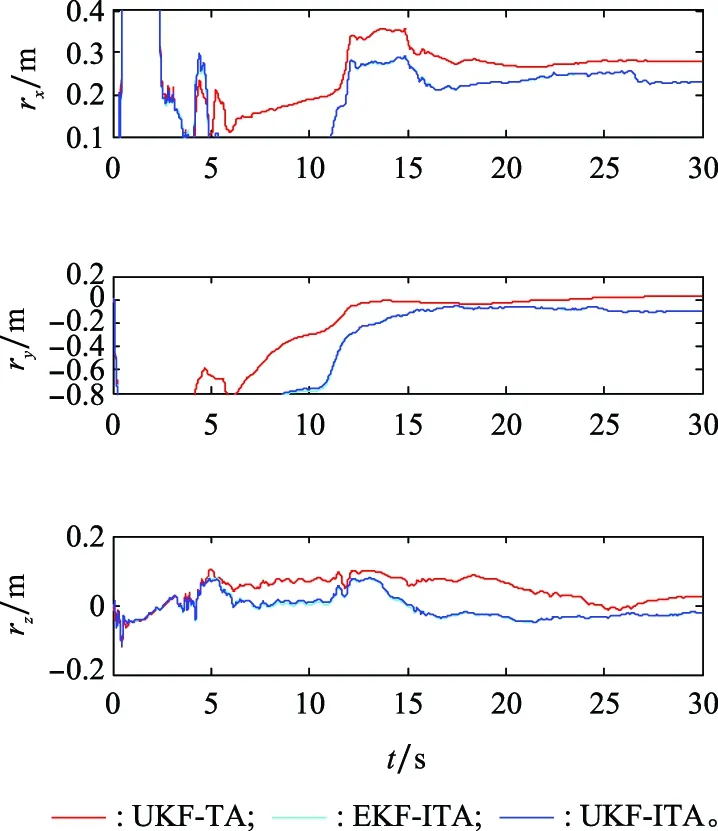
图15 杆臂误差rm估计结果Fig.15 Estimates of lever arm error rm

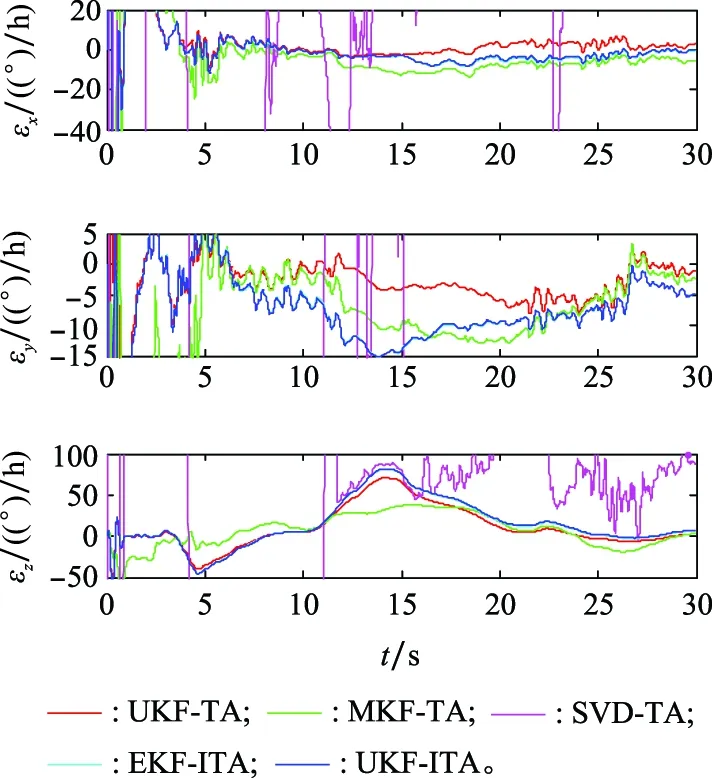
图16 陀螺仪零偏(启动零偏)估计结果Fig.16 Estimates of gyro bias (turn-on bias)

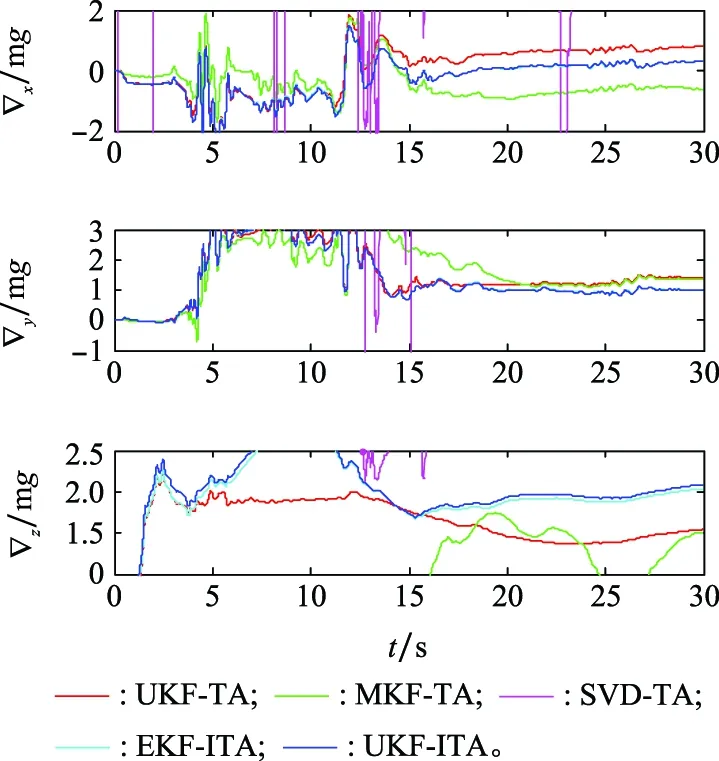
图17 加速度计零偏(启动零偏)估计结果Fig.17 Estimates of accelerometer bias (turn-on bias)

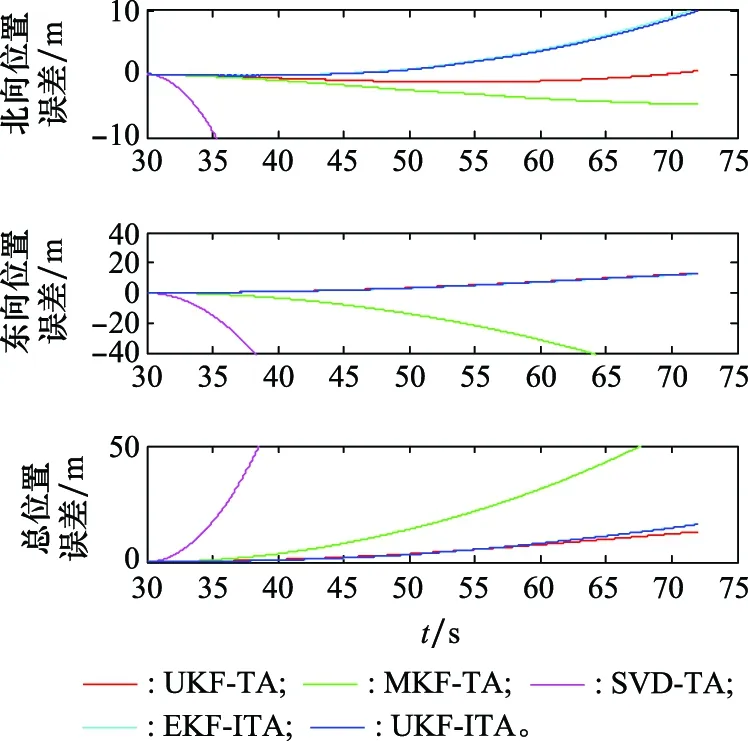
图18 纯惯性导航的定位误差Fig.18 Position errors of pure inertial navigation

由安装误差角的估计结果可以看出,由于估计了杆臂误差,从整体效果而言,UKF-TA、EKF-ITA和UKF-ITA要优于SVD-TA和MKF-TA。然而,如前文介绍,由于无法获知真实的安装误差角,以及杆臂误差和传感器零偏,所以无法对UKF-TA、EKF-ITA和UKF-ITA的精度高低进行评判。

由于纯惯性导航的定位误差与初始姿态误差和传感器误差具有直接关系,定位误差可以作为评判传递对准精度的重要依据。从图18可以看出,UKF-TA、EKF-ITA和UKF-ITA的定位误差相似,要远小于MKF-TA和SVD-TA,这也间接说明了UKF-TA、EKF-ITA和UKF-ITA的传递对准精度要优于MKF-TA和SVD-TA。由于IMU和PHINS之间的安装误差角很小,当IMU直接装订PHINS姿态时,传统的角误差模型为线性模型,所以UKF-TA的传递对准精度与EKF-ITA和UKF-ITA无明显差异。

为了验证在大失准角下UKF-TA的传递对准性能,本文在PHINS初始姿态中人为加入姿态误差([15°;15°;30°]),再装订给IMU,最终的定位误差如图19所示。

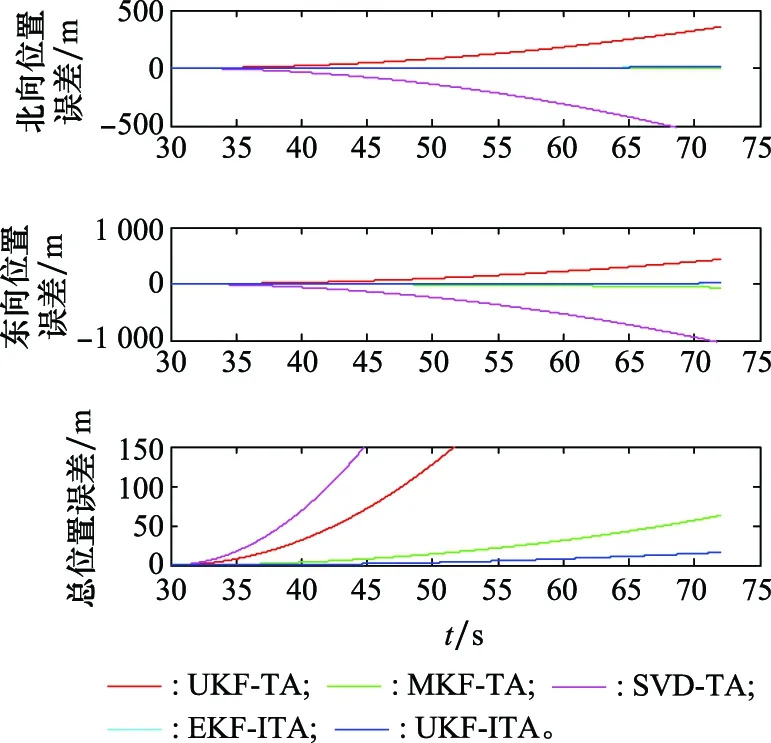
图19 纯惯性导航的定位误差(大失准角)Fig.19 Position errors of pure inertial navigation (large misalignment angles)

由图19可以看出,当人为加入姿态误差后,UKF-TA的定位精度明显下降,这也间接验证大失准角下UKF-TA的传递对准精度相对较低。

6 结 论

针对传统的传递对准模型在大失准角下的强非线性问题以及由残余杆臂误差导致的对准精度下降问题,提出了一种改进的惯性系传递对准算法。在惯性系框架下,建立了关于罗德里格斯参数和残余杆臂误差的具有弱非线性量测方程的传递对准模型,相比于传统的传递对准算法,系统维数相同,但系统的非线性度极大降低;相比于现有的惯性系传递对准算法,充分考虑了残余杆臂误差的影响。仿真实验表明,提出的算法在对准精度和传感器标定精度方面均优于现有方法,车载试验结果也间接说明提出的算法具有更高的传递对准性能。