基于时间相关性的梯度追踪多用户检测算法

蒋 芳, 杨雅情, 郑国梁, 王 翊, 许耀华,*, 吴香情

(1. 安徽大学计算智能与信号处理教育部重点实验室, 安徽 合肥 230601;2. 安徽省物联网频谱感知与测试工程技术研究中心, 安徽 合肥 230601)

0 引 言

根据物联网市场研究机构IoT Analytic预测:随着物联网产业的发展,通信网络中部署的物联网节点数量到2025年将达到215亿台,大规模机器类型通信(massive machine type communication, mMTC)会成为未来移动通信系统的重要应用场景。区别于人对人通信,mMTC面向控制类物联网,如远程抄表、环境监测、设备控制以及大型基础设施监控等,数据流以上行通信为主,且具有短包突发性特征。同时为了满足5G通信系统对于时延、信令开销以及接入效率的需求,免调度的非正交多址(grant-free non-orthogonal multiple access, GF-NOMA)接入技术在mMTC中被广泛研究。与长期演进(long term evolution, LTE)系统不同,GF-NOMA系统需要在接收端辨别用户的数据和活跃性。基于mMTC零星、突发性业务特征,其数据帧结构具有稀疏特性,因此可以使用压缩感知(compressed sensing, CS)的信号重建技术对设备的活跃性和数据进行联合检测。Abebe等人利用机器类型设备在一帧信号内活跃状态的结构性对子空间追踪(subspace pursuit, SP)算法进行了改进,提出了结构化迭代支撑检测(structured iterative support detection, SISD)算法,降低了误符号率(symbol error rate, SER)。文献[20]利用一帧信号内活跃设备的短持续性,结合正交匹配追踪(orthogonal matching pursuit, OMP)算法设计了基于结构匹配追踪的动态多用户检测(structured matching pursuit-based dynamic multi-user detection, SMP-MUD)算法,在每次迭代挑选1个活跃设备并使用最小二乘法计算估计信号值。文献[22]首先利用信号的块稀疏特性,结合阈值设置对SP算法进行了改进,通过选择合适的阈值提升了数据检测的准确性;其次,引入了机器学习的方法优化迭代终止条件,为多用户检测算法的研究提供了有意义的参考。以上基于CS的多用户检测,在数据检测阶段大多使用最小二乘法,需要对等效信道矩阵进行求逆,产生了较高的计算复杂度。

对基于CS的多用户检测算法而言,算法的计算复杂度不仅与信号值估计有关,还与迭代次数有关。基于CS的多用户检测算法中的每次迭代需要完成两个目标:设备的活跃性鉴别和活跃设备的发送数据检测。如果一次迭代能够检测出多个设备的活跃性并恢复这些设备的发送数据,势必能更快地完成检测。文献[23]利用活跃设备在一帧信号内的相邻时隙间具有时间相关性,设计了动态的CS多用户检测(dynamic CS-based multi-user detection, DCS-MUD)算法,每个时隙的初始支撑集都来自前1个时隙的检测结果,提高了设备活跃性鉴别的效率。文献[24]基于DCS-MUD算法框架,使用质量评估参数对获取的支撑集进行评估,剔除了错误索引,进一步提升了多用户检测的SER性能。文献[25]利用Dice系数匹配准则和最小二乘法提出了一种改进稀疏度自适应匹配的多用户检测算法,当相邻迭代残差信号比值大于阈值时使用大步长挑选多个设备,当相邻迭代残差信号比值小于阈值时使用小步长精确逼近。文献[26]通过自适应阈值辅助策略,在每次迭代时至少挑选1个活跃设备,之后再通过最小二乘法计算估计信号值。文献[27]通过设置最优索引数目,利用广义正交匹配追踪(generalized orthogonal matching pursuit,GOMP)算法,在每次迭代时挑选最优索引数目个数的活跃设备加入支撑集。

为降低基站端多用户检测复杂度,本文结合了时间相关性特征和梯度追踪(gradient pursuit, GP)算法,提出了相关性辅助的GP多用户检测(correlation-assisted multi-user detection, CAGP-MUD)算法。在设备的活跃性检测阶段,利用活跃设备在相邻时隙间的时间相关性,减少单个时隙内的迭代次数;在活跃设备的发送数据恢复阶段,采用GP算法避免由最小二乘导致的矩阵求逆。随后,在CAGP-MUD算法框架内引入决策衰弱的思想,增加每次迭代挑选出的活跃设备数目,进一步降低了单个时隙内的迭代次数,从而提高收敛速度,可被称之为相关性辅助的组梯度追踪多用户检测(correlation-assisted group gradient pursuit multi-user detection, CAGGP-MUD)算法。提出的算法分别从避免矩阵求逆和减少迭代次数两个角度,有效降低了复杂度,而GP算法的引入仍能保证算法的收敛性。因此,CAGP-MUD算法和CAGGP-MUD算法以较小的精度代价,换取了复杂度的有效降低。

1 系统模型

假设一个单基站(base station, BS)的上行免调度NOMA系统,覆盖个设备用户。为简化系统模型,只考虑每个设备用户配置单根天线的情况。根据mMTC的数据流特征,在一帧信号的持续时间内,仅有个设备处于有数据包发送的活跃状态,其他设备均处于休眠状态。活跃设备将其发送数据利用星座图进行符号映射,休眠状态的设备不发送数据。

因采用免调度机制,基站端首先要根据接收信号对设备的活跃性进行鉴别。为了对所有设备用户的发送符号数据进行统一表示,对传统的星座图进行了扩充,定义一个新的星座图={∪0}。当第个设备为活跃设备,则其发送的数据经星座图映射后表示为符号数据⊂;当第个设备为静默设备,没有数据包发送,该设备发送的符号数据可表示为=0。进行星座扩充后,无论设备用户是否活跃,都有⊂。

根据可压缩接入理论,设备的发送数据经由长度为的扩频码扩频到个子载波信道上。所有活跃设备的发送数据都采用相同的方式扩频到这个子载波信道上。考虑到NOMA系统的特征,子载波信道数≪设备用户数。BS的接收信号可表示为

(1)

式中：表示设备在第个子信道的信道增益系数;=[,,…,]是高斯白噪声,满足0均值,方差为。式(1)可以改写为

=+

(2)

式中:

定义为等效信道矩阵;=[,,…,]。

2 基于时间相关性的GP-MUD算法

2.1 CAGP-MUD算法

如前文所述,多用户检测算法的计算复杂度不仅与信号估计有关,还与迭代次数有关。为了降低多用户检测算法的复杂度,本文首先提出了CAGP-MUD算法,利用活跃设备的时间相关性特征减少多用户检测的迭代次数,利用GP算法降低发送数据恢复时的计算复杂度。

文献[23]指出,活跃设备有很大概率连续传输数据。因此,一帧信号持续时间内大部分活跃设备在相邻两个时隙的活跃性保持不变。在实际的通信场景下,会有少量设备在一帧信号持续时间内随机地接入或离开信道。因此,在帧结构上本文使用和文献[23]一致的混合稀疏模型,该模型认为在一帧信号持续时间内,大部分设备的活跃性保持不变,少部分设备的活跃性发生改变。混合稀疏模型把活跃性不发生改变的活跃设备称为公共活跃用户,将其索引的集合称为公共活跃用户支撑集;活跃性发生改变的活跃设备称为动态活跃用户,其索引的集合称为动态活跃用户支撑集。假设第时隙的活跃设备索引集合为,=∪。而第+1时隙的活跃设备索引+1=∪+1。因此,前一时隙检测出的活跃用户支撑集包含着大量有效的信息,完全可以用作下一时隙初始的支撑集。CAGP-MUD算法就是利用相邻两时隙间设备活跃状态的相关性避免每个时隙都从空集开始检测设备的活跃性,减少了从第二时隙往后的迭代次数。

目前大部分基于贪婪类算法的压缩感知多用户检测方法,在发送数据的恢复阶段都采用最小二乘计算,该阶段执行一个信道等效矩阵的伪逆运算,大规模应用时复杂度较高。CAGP-MUD算法结合GP框架,利用梯度下降法计算每次迭代的更新方向。

CAGP-MUD算法的具体细节如算法1所示。

算法1 CAGP-MUD算法输入 活跃设备数目:K;接收信号:y1,y2,…,yJ;等效信道矩阵:A输出 活跃设备及设备数据:x^i-11,x^i-12,…,x^i-1J初始化 Γ^=⌀,j=1,2,…,Jforj=1:Jdoi=1r0j=yjε=infΓij=Γ^whileε>thresholddoΓij=Γi-1j∪argmax|gj|2,wheregj=AHr(i-1)jdij=-gΓij,gΓij⊂gjcij=AΓijdijaij=〈rij,cij〉cij22x^iΓij=x^i-1Γij+aijdij

rij=ri-1j-aijcijε=rij2-ri-1j2i=i+1endwhileifΓij0≥KΓij={取x^iΓij中幅度最大的K个索引}endifΓ^=Γijx～i-1j,Γ^=x^i-1Γ^endfor

在CAGP-MUD算法的初始,会进行信息初始化,令初始活跃用户支撑集为空集。

首先,CAGP-MUD算法需要计算当前迭代的梯度值。梯度可表示为

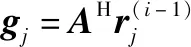
(3)

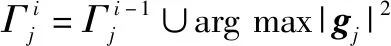
(4)

在CAGP-MUD算法中,使用梯度下降法计算每次迭代的更新方向。当前迭代的更新方向为梯度的负方向

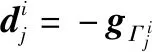
(5)

接着,CAGP-MUD算法需要更新每次迭代的估计信号值:

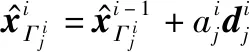
(6)

在CAGP-MUD算法的迭代执行过程中,需要对支撑集进行修剪。因为在单个时隙的内循环中,每执行一次迭代,支撑集会增加一个活跃设备的索引,当迭代次数大于某一数值后,支撑集规模大于活跃设备数目,此时支撑集中必定包含了错误的索引。此外,由于利用了活跃设备状态的时间相关性,每个时隙支撑集的初值来自于前一时隙的结果,该初始支撑中不仅包含对当前时隙有效的公共活跃支撑,也包含不属于当前时隙的错误支撑。因此,算法1需要使用活跃设备数目对支撑集进行修剪。

2.2 CAGGP-MUD算法

CAGP-MUD算法结合了GP框架和一帧信号持续时间内相邻时隙间设备活跃状态的相关性,有效降低了多用户检测算法的计算消耗。但是CAGP-MUD算法在每次迭代中只挑选一个活跃设备,挑选出所有活跃设备需要的迭代次数较多。为了减少单个时隙的迭代次数,本文在CAGP-MUD的基础上,结合决策衰弱策略,设计了CAGGP-MUD算法。利用决策衰弱思想,引入衰弱系数对最大梯度值进行衰弱,记为max||,并以此作为阈值。每次迭代挑选梯度信息大于该阈值的所有原子。相比于设定额定阈值的其他多用户检测算法,CAGGP-MUD算法利用每次迭代的最大梯度值和衰弱系数,动态设定阈值,沿负梯度方向一次挑选出多个活跃用户,减少了总的迭代次数。

CAGGP-MUD算法的具体细节如算法2所示。在活跃设备的鉴别阶段,CAGGP-MUD算法按照式(3)计算所有设备用户的梯度,根据计算结果,挑选梯度大于阈值的所有个设备,将设备索引加入到如下支撑集中：

(7)

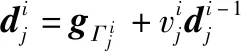
(8)

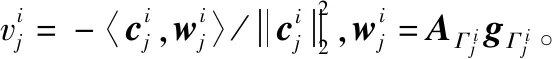
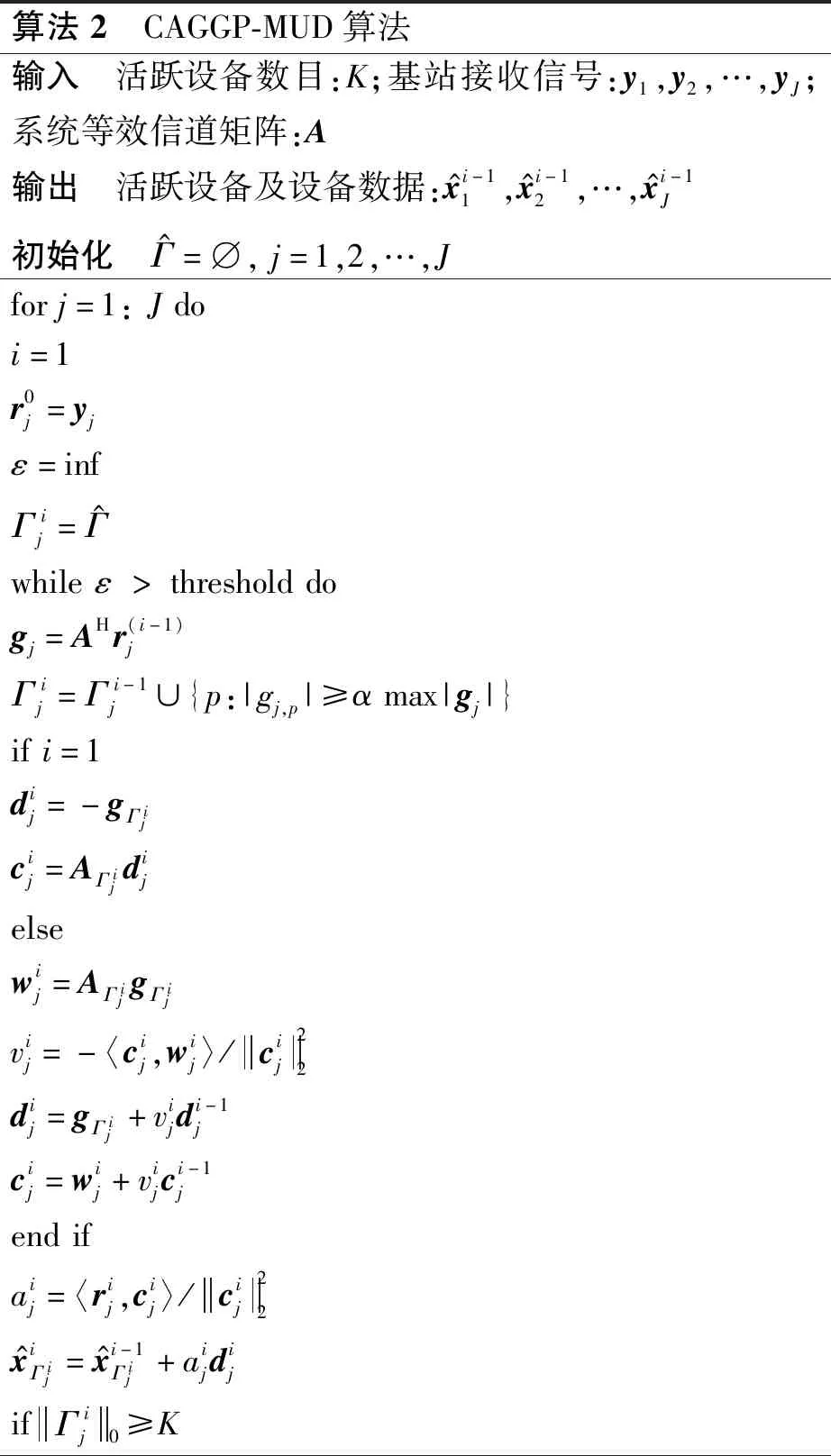
算法2 CAGGP-MUD算法输入 活跃设备数目:K;基站接收信号:y1,y2,…,yJ;系统等效信道矩阵:A输出 活跃设备及设备数据:x^i-11,x^i-12,…,x^i-1J初始化 Γ^=⌀,j=1,2,…,Jforj=1:Jdoi=1r0j=yjε=infΓij=Γ^whileε>thresholddogj=AHr(i-1)jΓij=Γi-1j∪{p:|gj,p|≥αmax|gj|}ifi=1dij=-gΓijcij=AΓijdijelsewij=AΓijgΓijvij=-〈cij,wij〉/cij22dij=gΓij+vijdi-1jcij=wij+vijci-1jendifaij=〈rij,cij〉/cij22x^iΓij=x^i-1Γij+aijdijifΓij0≥K

Γij={取x^iΓij中幅度最大的K个索引}endifrij=ri-1j-aijcijε=rij2-ri-1j2i=i+1endwhileΓ^=Γijx～i-1j,Γ^=x^i-1Γ^endfor

3 算法分析和仿真结果

3.1 复杂度分析

同文献[30]保持一致,采用每种算法的乘法浮点次数表示其复杂度。

CAGP-MUD和CAGGP-MUD两种算法都利用了时间相关性,即从第二个时隙开始,当前时隙的初始支撑集来自于前一个时隙的检测结果。因此,在一帧信号的检测过程中,两种算法都在第一个时隙将支撑集的初始值设置为空集,需要遍历所有设备的梯度才能挑选出活跃设备。从第二个时隙开始,可以利用前一个时隙的支撑集作为当前时隙支撑集的初始值,只需并入新的设备索引并通过支撑集裁剪对错误索引进行剔除。在进行复杂度计算时,按照第一时隙和其他时隙分别计算。

第一时隙中,CAGP-MUD算法的更新方向为梯度方向,由于选择了梯度方向作为每次迭代的更新方向,省去了更新方向计算。因此,CAGP-MUD算法的每次迭代需对步长、信号值和残差进行计算。复杂度表示为

=

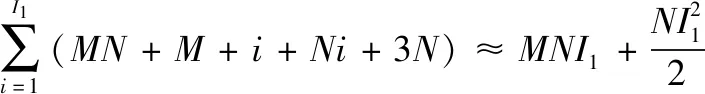
(9)

式中：表示迭代次数,下标1表示第一时隙。而CAGGP-MUD算法需要根据式(8)重新计算更新方向,增加了额外的复杂度消耗,执行共计+2+次浮点运算。在第一时隙,CAGGP-MUD算法的复杂度为

=

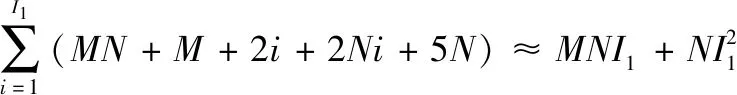
(10)

其他时隙中,两种算法的支撑集初始值均被赋值为前一时隙检测的结果。CAGP-MUD算法的计算复杂度表示为

+

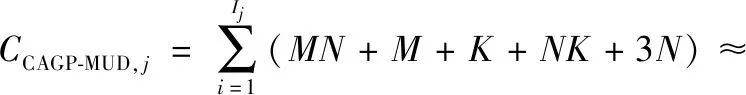
(11)

CAGGP-MUD算法的计算复杂度同样增加了相应的更新方向消耗

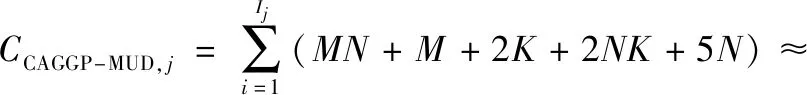
+2

(12)

式中：表示迭代次数,下标表示对应的时隙。将第一时隙和其他时隙的复杂度累加,得到各算法总的计算复杂度为

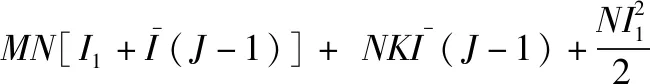
(13)

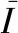
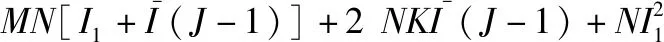
(14)

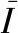
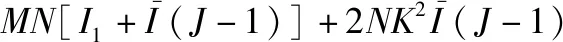
(15)

综合以上不同算法的复杂度算式,可以发现当系统内总的设备数量、活跃设备数量、占用的子载波信道数、帧长度保持一致时,多用户检测算法的计算消耗取决于迭代次数。

3.2 仿真结果及分析

在第31节中,论文分析了3种算法的计算复杂度,给出了总的复杂度算式。为了直观地表示不同算法的计算复杂度对比,对这3种同类算法进行了仿真实验。实验参数设置如下:总设备数量=200,其中活跃设备数量=20,占用的子载波信道数=100,一帧信号内总的时隙数=7,衰弱参数=09,信噪比分别取SNR=5 dB和SNR=10 dB。

根据复杂度分析的结论,迭代次数越多复杂度越高,且其分布具有随机性。因此,论文进行了1 000帧检测,取其平均迭代次数,结果如图1所示。DCS算法与CAGP-MUD算法在所有时隙均具有相近的迭代次数,而CAGGP-MUD算法在所有时隙的迭代次数均明显减少。这是因为前两者采用了相同的基于时间相关性的活跃设备检测方法,且每次迭代仅挑选出一个活跃设备。CAGGP-MUD算法由于采用了衰弱策略,一次迭代能够挑选出多个活跃设备,有效降低了迭代次数。在信噪比为5 dB和10 dB时分别进行实验,可以看出,DCS算法和CAGP-MUD算法在低信噪比时迭代次数相比高信噪比时有所增加,但CAGGP-MUD算法的迭代次数保持不变。这是因为DCS算法和CAGP-MUD算法在低信噪比下进行活跃设备检测时,会反复将某些设备选择和剔除,导致迭代次数变多。而CAGGP-MUD算法每次迭代挑选出多个活跃设备后,再根据信号估计值的大小进行支撑集修剪,优化了活跃设备的选择,减少了某些设备被反复迭代的情况,即使在低信噪比下仍能保持较少的迭代次数。此外,从图1可以看出,这3种算法在第一个时隙需要迭代的次数明显多于其他时隙,符合论文对于该类算法复杂度分析的结论。这一实验结果也进一步验证了文献[25]的观点,即利用一帧信号中相邻时隙间设备所具有的时间相关性可以减少从第二时隙开始的其他时隙的迭代次数。

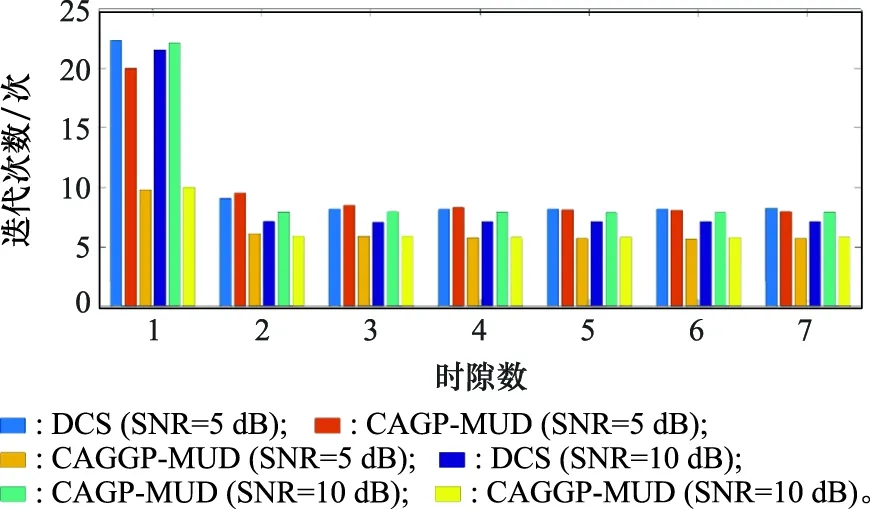
图1 不同算法完成1 000次实验每个时隙需要的平均迭代次数对比图Fig.1 Comparison of the average iterations required for each slot to complete 1 000 experiments with different algorithms

图1仅展示了迭代次数,不能完整地表示出各个算法的实际计算消耗,因此在迭代次数实验的基础上计算了各算法完成一次实验的总复杂度,并绘制了如图2所示的量化对比图。为了不失一般性,增加了与SMP算法、基于梯度下降的梯度追踪MUD(gradient descent-based gradient pursuit MUD, GDGP-MUD)算法和基于多步拟牛顿法的梯度追踪MUD(multi-step quasi-Newton MUD, MSQN-MUD)算法的对比。图2的结果显示,在6种比较算法中,本文提出的 CAGP-MUD算法和CAGGP-MUD算法计算复杂度较低。与SMP算法相比,CAGP-MUD算法的计算复杂度仅为SMP算法的15.4%,CAGGP-MUD算法甚至低至SMP算法的11.5%;与DCS算法相比,CAGP-MUD算法的计算复杂度约为DCS算法的33%,CAGGP-MUD算法甚至低至DCS算法的24.6%。由此可见,所提出的两种算法结合了时间相关性特征和GP,从降低迭代次数和避免矩阵求逆运算两个角度,降低了多用户检测的复杂度。而CAGGP-MUD算法则通过引入衰弱策略,进一步降低了计算复杂度。

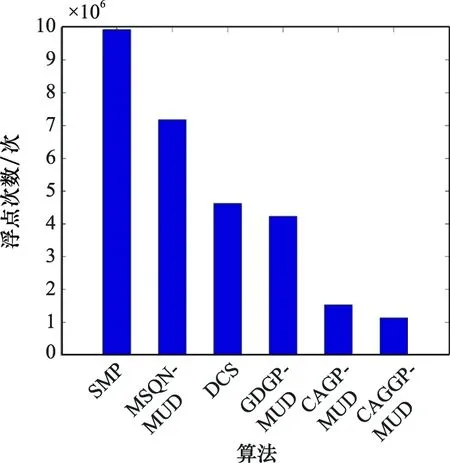
图2 不同算法计算消耗对比图Fig.2 Comparison of computational cost of different algorithms

图3给出了各算法在不同信噪比条件下的SER对比情况,其他实验参数同上文一致。从图3可以看出,CAGP-MUD算法和CAGGP-MUD算法在低信噪比的环境下SER性能接近或略优于DCS算法,但是在高信噪比的环境下检测精度有所损失。图3中普通最小二乘法(ordinary least squares, OLS)曲线代表理想状态下最小二乘法的检测精度。也就是说,提出的算法以有限的检测精度代价换取了复杂度的有效降低。

图3 不同算法SER性能对比图Fig.3 Comparison of SER performance of different algorithms

图4给出了不同活跃设备数情况下CAGP-MUD算法、CAGGP-MUD算法与DCS算法的SER性能对比图。CAGGP-MUD算法利用决策衰弱,以每次迭代的梯度值乘以衰弱系数作为动态阈值,相比于设定额定阈值的方法,即使活跃设备数目较低也不会限制CAGGP-MUD算法的应用。

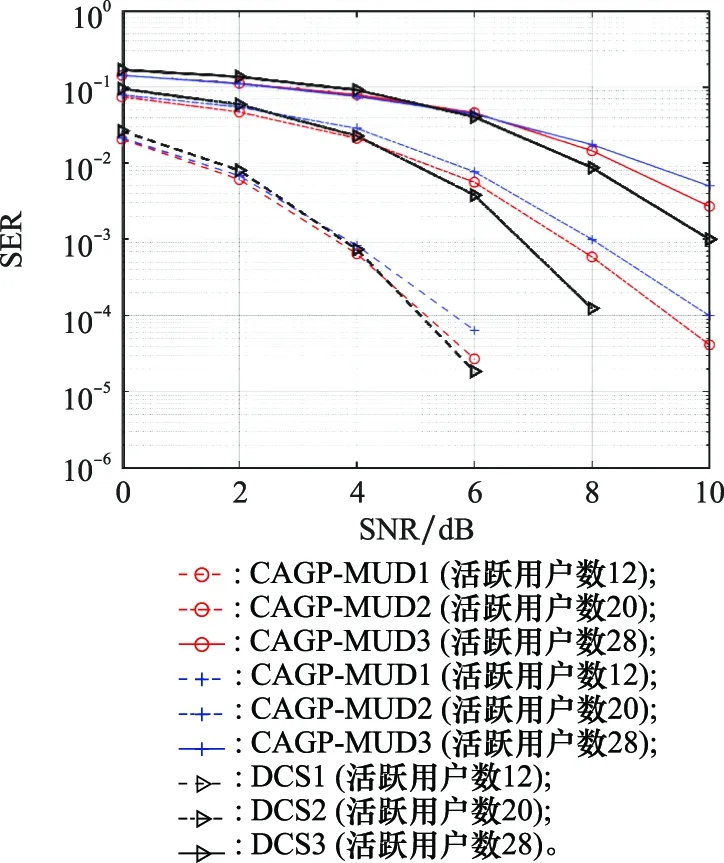
图4 活跃设备数变化时算法的SER性能对比图Fig.4 SER performance comparison with the number of active devices

图5给出了衰弱参数对CAGGP-MUD算法的SER性能影响的对比图。当信噪比较小时,衰弱参数的取值对精度影响不大,而当信噪较大时,取较大的衰弱参数会使得SER精度提升。在实际操作中,当系统中噪声较大时,可采用较小的衰弱参数来加快检测。随着信噪比逐渐增大,衰弱参数对CAGGP-MUD算法SER 性能的影响越来越大。因此,当系统中的噪声较小时,需选用较大的衰弱参数。

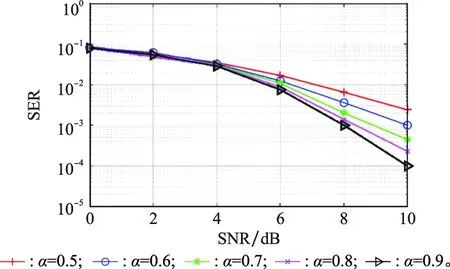
图5 衰弱参数α对CAGGP-MUD算法的SER性能影响对比图Fig.5 Comparison of the weakening influence parameter α on the SER performance of CAGGP-MUD algorithm

图6给出了当SNR=10 dB时,CAGGP-MUD算法每次迭代挑选的活跃设备个数随衰弱参数变化的对比图,纵坐标为1 000次实验及所有时隙的迭代次数的平均值。从图6可以看出,衰弱参数越小,CAGGP-MUD算法每次迭代挑选出的活跃设备数越多,尤其是在前几次迭代中,这种影响更加明显。当迭代次数超过5以后,衰弱参数对每次迭代挑选的活跃设备数的影响降低;当迭代次数超过9以后,衰弱参数的改变对每次迭代挑选的活跃设备数几乎没有影响。

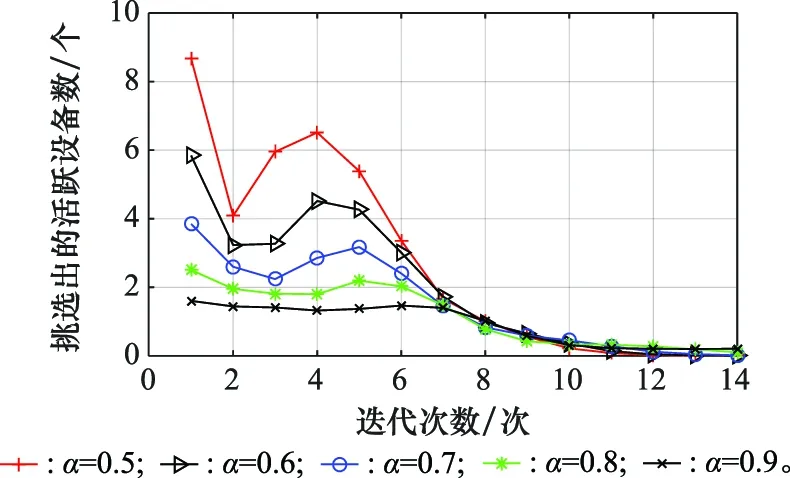
图6 衰弱参数α对每次迭代挑选出的活跃设备数的影响对比图Fig.6 Comparison of weakening influence parameters α on the number of active devices selected in each iteration

4 结束语

本文分析了mMTC中基于压缩感知的多用户检测算法的复杂度问题,结合活跃设备的时间相关性特征和梯度追踪算法,提出了CAGP-MUD算法。算法将前一时隙使用梯度追踪挑选并裁剪后的支撑集赋值给当前时隙作为初始支撑集,通过多次梯度计算更新支撑集并估计活跃设备的信号值。该算法有效降低了多用户检测的复杂度,但每次迭代仅挑选出一个活跃设备。进一步,在CAGP-MUD算法框架内引入了决策衰弱策略,提出了CAGGP-MUD算法。CAGGP-MUD算法使用衰弱参数对每次迭代的梯度最大值进行衰弱,并将其作为阈值,挑选梯度信息大于阈值的所有设备,将其索引加入支撑集,通过一次迭代挑选出多个活跃设备,更快地完成检测。实验结果表明,CAGP-MUD算法和CAGGP-MUD算法降低了多用户检测算法的复杂度。