经历平行四边形面积公式的推导过程

文|游 凌

怎样帮助学生经历平行四边形面积计算公式的推导过程，可以采用如下教学过程。

一、呈现问题，自主尝试

提供材料：练习纸上印有1 个平行四边形（底6cm，高4cm，邻边5cm）和一张透明格子图。出示任务：请你测量所需要的数据，尝试计算平行四边形的面积。学生尝试解决，组内交流。全班交流，展示学生典型作品（如图1、图2）。

图1

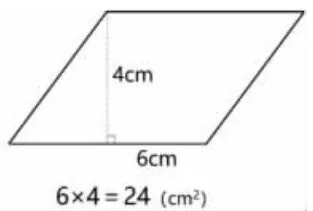
图2

思考：两位同学分别是怎么计算的？你赞同哪种计算方法？为什么？预设学生用数格子的方法来验证。学生借助网格纸数一数（图3）。小组反馈：数的结果是多少？你是怎么数的？遇到不是半格怎么数？通过数格子发现结果是24cm2，所以“6×4”是正确的，“6×5”是错误的。

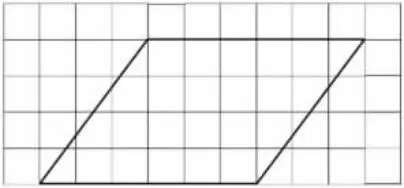
图3

二、动手操作，感悟关系

思考：为什么“6×5”是错误的？“6×5”算的是哪个图形的面积？通过动手操作和课件演示，发现“6×5”算的是长6cm、宽5cm 的长方形（图4），通过对比，发现长方形比平行四边形的面积大。

图4

思考：“6×4”你们又是怎么想的？预设学生通过割补的方法（图5），将其转化成长方形。

图5

思考：在割补过程中，面积有没有变化？通过交流发现面积不变，再让学生寻找长方形和平行四边形对应的数量关系。预设学生发现长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，长方形的面积等于平行四边形的面积。

三、巩固运用，内化提高

计算下面图形的面积。

思考：1.在计算过程中，你想到了怎样一个长方形，请你在图中描一描。2.计算面积时，对于底和高有什么要求？强调底和高要对应。

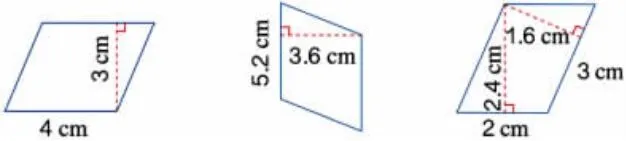
图6

学生经历猜想、操作、验证和推理的过程，体会转化思想，从而有效的帮助学生经历平行四边形面积计算公式的推导过程。