有限元法提取寄生参数的宏敏感度模型

张 程，徐小宇

（1.中国科学院微电子研究所，北京 100029；2.中国科学院大学，北京 100049）

在集成电路（IC）设计过程中，寄生参数提取的精度问题是一个非常重要的议题，它取决于基于麦克斯韦方程组的电磁场求解器，通过求解器进行参数提取往往会耗费大量的时间与资源，不符合当前集成电路设计中快速签核的目标。宏模型通常是原始物理系统的简化等效模型，它保留了原系统的基本物理属性，能够提高系统分析的速度、节省计算时间。近几年来，宏模型还被用来保护设计中的知识产权，作为黑盒子来模糊处理敏感的设计或者工艺，达到加密的效果[1-4]；另一方面，集成电路制造技术的特征尺寸如今已发展至纳米级，工艺波动也是一个关键问题[5-9]。

在有限元法的基础上，文中提出一种敏感度模型，以扩大宏模型的应用范围。将该敏感度模型与宏模型进行结合，能够用来分析集成电路寄生参数的敏感度，从而为半导体厂商提供评估宏模型可靠性的方法，为电路设计者提供优化电路布局、提升整体电路设计效率的手段。

1 宏敏感度模型

1.1 宏模型

对集成电路电阻、电容等参数的提取需要通过麦克斯韦方程组求解电路的场分布，可以采用多种电磁场数值求解方法，如有限元法（FEM）、有限差分法（FDM）、边界元法（BEM）、浮动随机行走法（FRW）、矩量法（MoM）、多层快速多极子法等，这些方法各有利弊[1-15]。

电磁场数值求解方法都可用来生成宏模型，相应地，宏模型也可被上述方法进行调用[1]。需要注意的是，对于不同方法生成的宏模型，其构成元素的含义并不完全一致，因此在使用不同方法交叉调用宏模型时需要根据不同的含义在界面的节点或者面元上进行电势或者电通量的耦合。

在使用宏模型对相应电路进行参数提取时，为了保证精度和可靠性，需要对网格充分细化，必要时还可使用二阶基函数描述网格单元[3]。

下面以二维情形为例说明宏模型的构成。如图1所示，在多导体静电系统之中，两个导体结构位于接地衬底之上，其中，虚线标识的区域（导体#1 周围）为宏模型区域，导体#1 与导体#2 位于接地衬底（导体#0）上方。宏模型区域可以由任意形状的封闭曲面围成，也可以包含多个导体、多层介质。

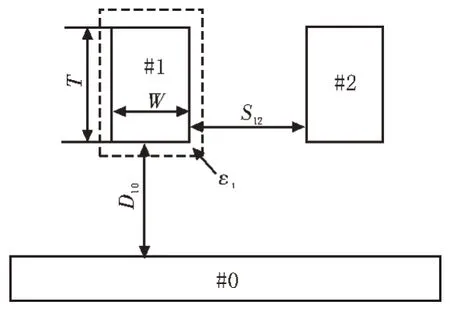
图1 多个导体的二维静电系统示意图

根据有限元法的基本求解过程，首先对计算区域进行空间体网格离散。对于电介质区域内的各个网格节点，设定电势Vi；对于导体表面的网格节点，设定电势Vc，注意这里不包括导体的内部节点，导体内部区域可以从计算区域之中去掉；对于宏模型表面上的节点，设定电势Vp，表面节点可以类比电路的端口（port）。上述的网格节点分别称为内部节点、导体节点、端口节点。对于集成电路结构中的浮导体，可以视为介电常数较大的介质类比处理。对于宏模型边界包含导体面的特殊情况，即部分端口节点是导体节点，其大致流程没有显著变化，文中仅就一般情况进行讨论。

通过有限元法构建的宏模型采用矩阵形式表达，记为矩阵KM，如式（1）所示[1]：

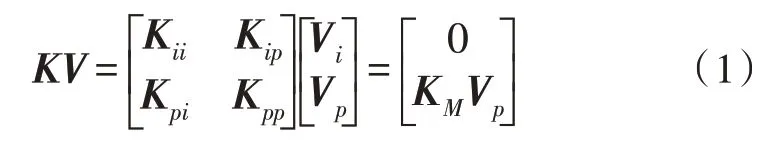
其中，K为有限元法生成的总体刚度矩阵，子矩阵Kii描述了内部节点间的相关关系，Kpp描述了端口节点间的相关关系，而子矩阵Kip和Kpi互为转置，描述了端口节点和内部节点间的相互联系。

向量Vi和宏模型矩阵KM之间的关系通过式（1）变换导出：

由此，可得到宏模型的组成，主要包括：

1）端口节点的坐标以及节点之间的关联关系；

2）宏模型矩阵KM。

生成该宏模型后，半导体制造厂商可以只将宏模型提供给设计者，由于宏模型区域只包含表面节点信息，不包含宏模型内部区域的细致结构信息，因此保护了重要敏感目标和相应的知识产权，如关键的工艺信息不会被竞争对手轻易获得。对于大量重复出现的结构，宏模型可简化计算，不用对此类结构内部进行反复建模分析。

1.2 宏敏感度模型的推导

当前，最先进的集成电路工艺特征尺寸处于纳米量级，并且继续向极限发展。制造过程中的工艺波动（也可称为变异或涨落）相对于电路线宽等尺寸的比例越来越显著，成为可制造性设计中不可回避的问题。敏感度分析是处理此类工艺变异问题的有效工具[6-7]。当集成电路的几何参数或材料参数发生变化时，它能够有效预测在标称尺寸下的参数提取结果。

基于有限元法，结合宏模型以及敏感度分析，文中提出了宏模型的敏感度模型，为方便起见，可称为宏敏感度模型。

给定一个设计参数p，该参数可以是几何参数（如导体宽度、厚度尺寸或者导体之间的距离）或材料参数（如绝缘介质层的介电常数）。将式（1）中的表达式分别对设计参数p求偏导，可得到：

将式（2）代入式（4），可获得Vi关于p的偏导数：

将式（2）、（3）和式（6）代入式（5），KM对设计参数p的偏导数可以写为：

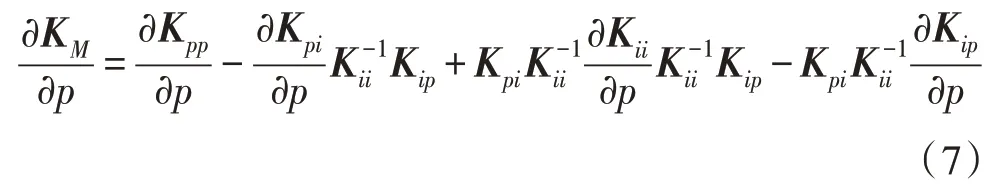
通常，由有限元法生成的矩阵KM和Kii是对称矩阵，从式（7）也可以看出，同样是对称矩阵。

根据上述推导，完整的一阶宏敏感度模型由如下三部分组成：

1）端口节点的坐标以及节点之间的关联关系；

2）宏模型KM；

2 应用

2.1 宏模型的应用

在结合有限元法使用宏模型时，除了宏模型所处的子区域，计算区域其余部分都需要进行网格离散。设基于有限元法所形成的总体刚度矩阵为M，根据节点所处的位置，其可分解为：

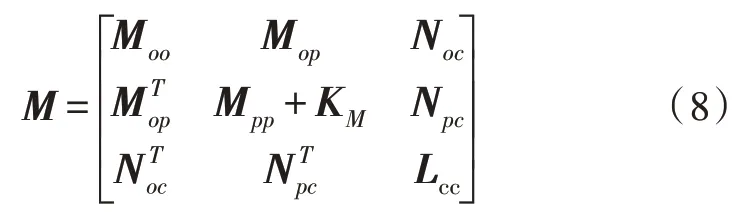
其中，Moo表示宏模型区域之外电介质内节点之间的本构系数，Mop表示内节点与宏模型端口节点之间的本构系数，Mpp表示宏模型端口节点之间的本构系数，KM表示宏模型，Noc表示内节点与导体面上节点之间的本构系数，Npc表示端口节点与导体面上节点之间的本构关系，Lcc表示导体面上节点之间的关系。

对于n个导体系统的电容参数矩阵提取来说，设定其中一个导体为主导体（施加1 V 电势），其他导体为环境导体（施加0 V 电势），可以得到：

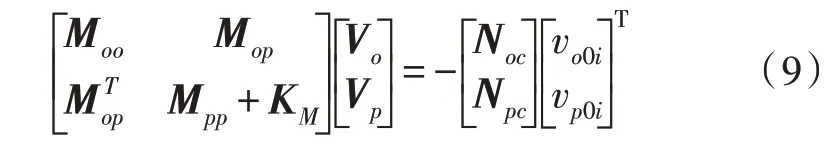
其中，Vo是施加在除宏模型区域之外的区域中电介质内节点上的电势，Vp是施加在宏模型端口节点上的电势，vo0i和vp0i表示在提取参数时施加在导体上的电势矢量，下标i表示第i个导体，导体i上施加1 V 电势，其他导体为0 V 电势。

求解方程式（10）可以得到电势分布ve。

需要注意的是，宏模型区域边界上的节点信息是既有存在的，在对计算区域进行网格剖分时，需要适应这些节点信息。如果计算区域不按照这些既定网格节点进行剖分，就会导致网格节点不匹配，这时需要在界面上进行插值和映射处理[16]。

2.2 宏敏感度模型的应用

采用同样的方式，将式（10）两边对参数p求偏导数，得到：

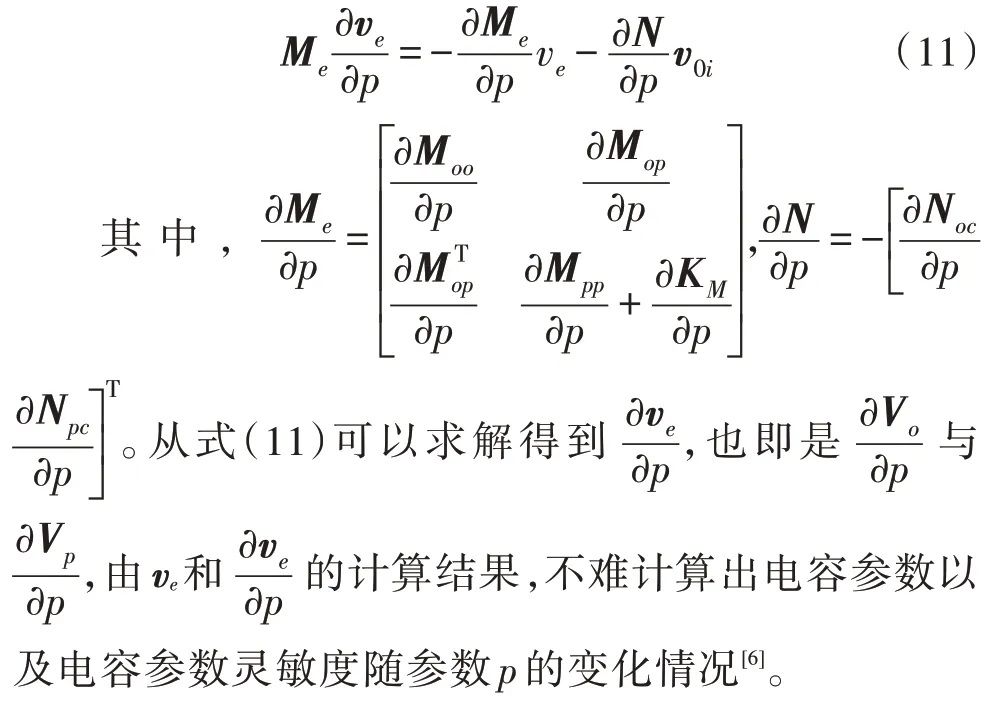
3 数值算例

分析上述推导过程可以发现，处理二维和三维参数提取问题的方法是一致的，并且与常规的有限元法形成的线性代数矩阵相比，在宏模型之外的区域没有差异，因此，为方便起见，可以只采用二维问题进行数值分析与验证。

如图1 所示算例，各标称尺寸分别为导体#1 宽度W为0.1 μm，厚度T为0.22 μm，导体#1 与导体#2的间距S12为0.24 μm，导体#1 与导体#0 的间距D10为0.50 μm。导体所处空间电介质的相对介电常数为εr=4.2。假设W和T分别有10%的变异程度，分别使用直接有限元法和灵敏度模型计算变异之后的电容，计算结果如表1 所示。

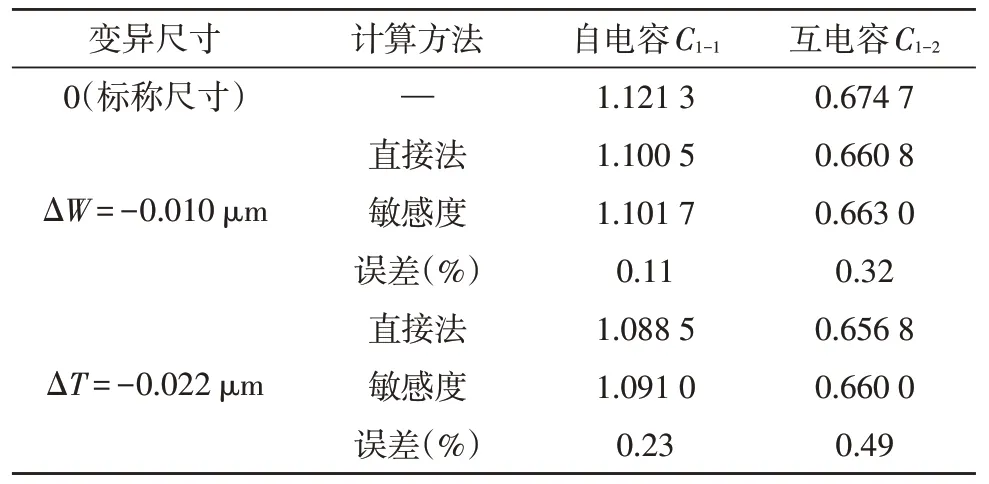
表1 采用不同方法获得的电容提取结果（单位长度电容的单位：×105 fF）

由于宏模型的内部结构和材料信息被隐藏，在使用宏模型时，半导体制造商可以计算宏模型内所有导体的全电容矩阵，而设计机构只能将宏模型视为等效导体，并得到宏模型边界上的表面电荷。因为敏感度模型的精度受网格精度的影响较大，所以需要严格控制离散网格的密度以达到最优的求解性能。敏感度分析是在局部范围内进行的，因此只考虑宏模型内部（如图1中的T、W和ε1）和边界上（如图1中的S12和D10）的变化。

4 结论

文中提出了一种宏模型的敏感度模型用于集成电路寄生参数提取，并给出详细的实现与应用流程。与宏模型相比，该模型能够提供更多的局部场信息，可以用来预测工艺变异对寄生参数的影响。半导体制造厂商提供宏模型以加密电路结构时，能够通过它来评估宏模型的可靠性，而电路设计者则可以在仅掌握宏模型的信息基础上，以此来分析工艺变化对电路性能的潜在影响。